高中数学人教A版(2019)必修第一册3.1.2函数的表示法课时作业(含答案)
文档属性
| 名称 | 高中数学人教A版(2019)必修第一册3.1.2函数的表示法课时作业(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 137.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 09:44:31 | ||
图片预览



文档简介
3.1.2 函数的表示法
必备知识基础练
1.函数y=x-1(x≥0)的图象是( )
A.一条射线 B.一条线段
C.两条射线 D.一条直线
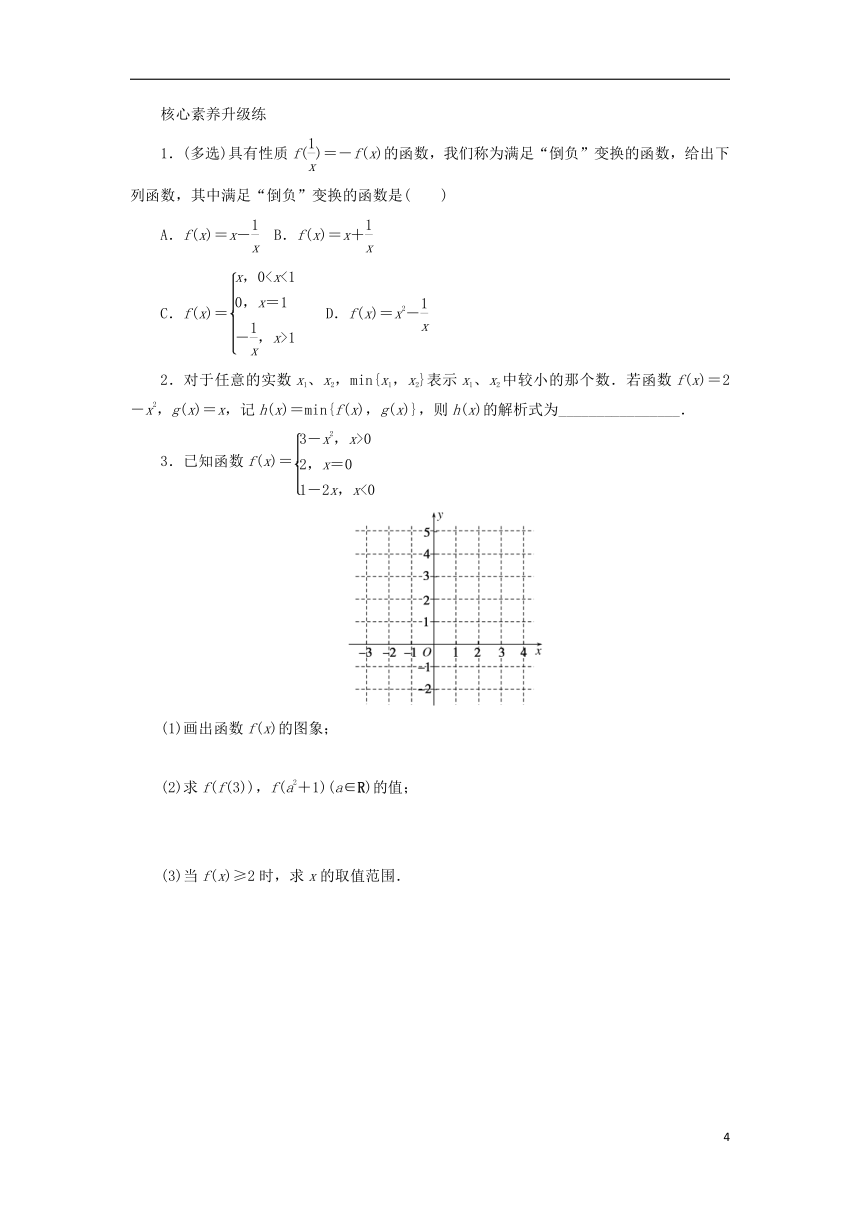
2.已知函数f(x)的对应关系如下表,函数y=g(x)的图象为如图所示的曲线ABC,其中A(1,3),B(2,1),C(3,2),则f(g(2))=( )
x 1 2 3
f(x) 2 3 0
A.3 B.2 C.1 D.0
3.已知f(x)是反比例函数,且f(-3)=-1,则f(x)的解析式为( )
A.f(x)=- B. f(x)=
C.f(x)=3x D.f(x)=-3x
4.已知函数f(x)=则f(f(-1))=( )
A.2 B. C.1 D.-1
5.已知函数f(x)和g(x)的定义域为{2,3,4,5},其对应关系如下表,则g(f(x))的值域为( )
x 2 3 4 5
f(x) 4 2 5 2
g(x) 4 3 2 4
A.{2,3} B.{2,4}
C.{3,4} D.{2,3,4}
6.(多选)下列给出的式子是分段函数的是( )
A.f(x)=
B.f(x)=
C.f(x)=
D.f(x)=
7.已知二次函数f(x)的图象经过点(-3,2),顶点是(-2,3),则函数f(x)的解析式为________.
8.[2022·广东梅州高一期末]已知f(2x-1)=x2-2x,则f(0)=________.
关键能力综合练
1.某学生离家去上学,一开始岀发,心情轻松,缓慢行进,后来发现时间比较紧,为了赶时间开始加速,走完余下的路程.下列图形中,纵轴表示离校的距离,横轴表示出发后的时间,则较符合该学生走法的是( )
2.已知函数f(x)=,若f(x)=5,则x的值是( )
A.-2 B.2或-
C.2或-2 D.2或-2或-
3.函数y=x+的图象是( )
4.已知函数f(x+1)=x2-2x+3,则函数y=f(x)的解析式为( )
A.f(x)=x2-6x+4 B.f(x)=x2-4x+6
C.f(x)=x2-4x-4 D.f(x)=x2-6x+11
5.已知函数f(x)是一次函数,且f[f(x)-4x]=5恒成立,则f(2)=( )
A.1 B.3 C.7 D.9
6.(多选)已知函数f(x)=若f(f(a))=2,则实数a的值为( )
A.-2 B.- C.-1 D.1
7.[2022·广东深圳高一期末]已知函数f(x)=,则f(f(5))=________.
8.已知函数f(x)满足f(x)+2f(-x)=2x+3,则f(x)=________.
9.已知函数f(x)=且f(2)=0.
(1)求f(f(1));
(2)若f(m)=-m,求实数m的值.
10.求下列函数的解析式.
(1)已知f(x)是一次函数,且满足3f(x+1)-2f(x-1)=2x+17,求f(x);
(2)若函数f()=x-1,求f(x).
核心素养升级练
1.(多选)具有性质f()=-f(x)的函数,我们称为满足“倒负”变换的函数,给出下列函数,其中满足“倒负”变换的函数是( )
A.f(x)=x- B.f(x)=x+
C.f(x)= D.f(x)=x2-
2.对于任意的实数x1、x2,min{x1,x2}表示x1、x2中较小的那个数.若函数f(x)=2-x2,g(x)=x,记h(x)=min{f(x),g(x)},则h(x)的解析式为________________.
3.已知函数f(x)=
(1)画出函数f(x)的图象;
(2)求f(f(3)),f(a2+1)(a∈R)的值;
(3)当f(x)≥2时,求x的取值范围.
3.1.2 函数的表示法
必备知识基础练
1.答案:A
解析:函数y=x-1为一次函数,图象为直线,但是当x≥0时,所得到的图象为一条射线.
2.答案:B
解析:观察函数y=g(x)的图象得:g(2)=1,由表格知:f(1)=2,所以f(g(2))=2.
3.答案:B
解析:设f(x)=(k≠0),
∵f(-3)==-1,∴k=3,
∴f(x)=.
4.答案:B
解析:根据题意,因为f(-1)=2,所以f(f(-1))=f(2)=.
5.答案:B
解析:g(f(2))=g(4)=2,g(f(3))=g(2)=4,g(f(4))=g(5)=4,g(f(5))=g(2)=4,所以所求值域是{2,4}.
6.答案:AD
解析:对于A:f(x)=,定义域为[1,5]∪(-∞,1)=(-∞,5],且[1,5]∩(-∞,1)= ,符合函数定义,且在定义域的不同区间,有不同的对应关系,故A正确;
对于B:f(x)=,定义域为R∪[2,+∞)=R,但R∩[2,+∞)=[2,+∞)≠ 不满足函数的定义,如当x=2时,f(2)=3和4,故不是函数,故B错误;
对于C:f(x)=,定义域为[1,5]∪(-∞,1]=(-∞,5],且[1,5]∩(-∞,1)={1},且f(1)=5和1,故不是函数,故C错误;
对于D:f(x)=,定义域为(-∞,0)∪[5,+∞),且(-∞,0)∩[5,+∞)= ,符合函数定义,且在定义域的不同区间,有不同的对应关系,故D正确.
7.答案:f(x)=-x2-4x-1
解析:根据顶点为(-2,3),设f(x)=a(x+2)2+3(a≠0),
由f(x)过点(-3,2),得2=a×1+3,
解得a=-1,
所以f(x)=-(x+2)2+3=-x2-4x-1.
8.答案:-
解析:令x=,则2x-1=0,所以f(0)=f(2×-1)=()2-2×=-.
关键能力综合练
1.答案:C
解析:由题意知:一开始岀发,心情轻松,缓慢行进,所以开始曲线比较平缓,后来发现时间比较紧,为了赶时间开始加速,所以曲线变得越来越陡峭,又因为纵轴表示离校的距离,横轴表示出发后的时间,所以开始距离最大,最后距离为0,故选C.
2.答案:A
解析:当x≤0时,f(x)=x2+1=5,解得:x=-2或x=2(舍),∴x=-2;
当x>0时,f(x)=-2x=5,解得:x=-(舍);
综上所述:x的值是-2.
3.答案:C
解析:对于y=x+,当x>0时,y=x+1;当x<0时,y=x-1.
即y=,故其图象应为C.
4.答案:B
解析:因为f(x+1)=x2-2x+3,
令t=x+1,则x=t-1,
则f(t)=(t-1)2-2(t-1)+3=t2-4t+6,
所以f(x)=x2-4x+6.
5.答案:D
解析:因为函数f(x)是一次函数,且f[f(x)-4x]=5恒成立,
令f(x)-4x=t,则f(x)=4x+t,
所以f(t)=4t+t=5,解得t=1,
所以f(x)=4x+1,f(2)=2×4+1=9.
6.答案:AB
解析:令f(a)=t,故f(t)=2,进而得t=-1或t=1,
所以f(a)=-1或f(a)=1,
由于x>0时,f(x)≥2,
所以3a+5=-1或3a+5=1,解得a=-2或a=-.
7.答案:1
解析:因为函数f(x)=,
所以f(5)=f(3)=f(1)=12=1,
所以f(f(5))=f(1)=12=1.
8.答案:-2x+1
解析:因为f(x)+2f(-x)=2x+3,①
所以f(-x)+2f(x)=2·(-x)+3,②
②×2-①得,f(x)=-2x+1.
9.解析:(1)∵f(2)=2a-1=0得a=,
∴f(x)=,
∴f(1)=-,
∴f(f(1))=f(-)=-2.
(2)当m≥0时,由f(m)=-m得m-1=-m解得m=;
当m<0时,由f(m)=-m得=-m,无实数解,
综上所述,m=.
10.解析:(1)因为f(x)是一次函数,设f(x)=ax+b,(a≠0),
则f(x+1)=a(x+1)+b,f(x-1)=a(x-1)+b,
所以3f(x+1)-2f(x-1)=ax+5a+b=2x+17,
则,解得,
所以f(x)=2x+7.
(2)由函数f()=x-1,
令=t≥0,则x=t2-1,
所以f(t)=t2-2,
所以f(x)=x2-2,x∈[0,+∞).
核心素养升级练
1.答案:AC
解析:对于选项A,f()=-x,-f(x)=-x,故满足“倒负”变换;
对于选项B,f()=+x,-f(x)=--x,故不满足“倒负”变换;
对于选项C,当0<x<1时,f()=-x,-f(x)=-x,当x=1时,f(1)=0,成立,当x>1时,f()=,-f(x)=,故满足“倒负”变换;
对于选项D,f()=,-f(x)=,故不满足“倒负”变换.
2.答案:h(x)=
解析:当f(x)≤g(x)时,即2-x2≤x,即x2+x-2≥0,解得x≤-2或x≥1,
此时,h(x)=min{f(x),g(x)}=f(x)=2-x2;
当f(x)>g(x)时,即2-x2>x,即x2+x-2<0,
解得-2此时,h(x)=min{f(x),g(x)}=g(x)=x.
综上所述,h(x)=.
3.解析:(1)函数f(x)的图象如图所示:
(2)f(f(3))=f(3-32)=f(-6)=1-2×(-6)=13,
f(a2+1)=3-(a2+1)2=-a4-2a2+2;
(3)当x>0时,f(x)≥2 3-x2≥2 -1≤x≤1,∴0当x=0时,f(x)=2,符合题意;
当x<0时,f(x)≥2 1-2x≥2 x≤-,
综上所述:x的取值范围为:(-∞,-]∪[0,1].
1
必备知识基础练
1.函数y=x-1(x≥0)的图象是( )
A.一条射线 B.一条线段
C.两条射线 D.一条直线
2.已知函数f(x)的对应关系如下表,函数y=g(x)的图象为如图所示的曲线ABC,其中A(1,3),B(2,1),C(3,2),则f(g(2))=( )
x 1 2 3
f(x) 2 3 0
A.3 B.2 C.1 D.0
3.已知f(x)是反比例函数,且f(-3)=-1,则f(x)的解析式为( )
A.f(x)=- B. f(x)=
C.f(x)=3x D.f(x)=-3x
4.已知函数f(x)=则f(f(-1))=( )
A.2 B. C.1 D.-1
5.已知函数f(x)和g(x)的定义域为{2,3,4,5},其对应关系如下表,则g(f(x))的值域为( )
x 2 3 4 5
f(x) 4 2 5 2
g(x) 4 3 2 4
A.{2,3} B.{2,4}
C.{3,4} D.{2,3,4}
6.(多选)下列给出的式子是分段函数的是( )
A.f(x)=
B.f(x)=
C.f(x)=
D.f(x)=
7.已知二次函数f(x)的图象经过点(-3,2),顶点是(-2,3),则函数f(x)的解析式为________.
8.[2022·广东梅州高一期末]已知f(2x-1)=x2-2x,则f(0)=________.
关键能力综合练
1.某学生离家去上学,一开始岀发,心情轻松,缓慢行进,后来发现时间比较紧,为了赶时间开始加速,走完余下的路程.下列图形中,纵轴表示离校的距离,横轴表示出发后的时间,则较符合该学生走法的是( )
2.已知函数f(x)=,若f(x)=5,则x的值是( )
A.-2 B.2或-
C.2或-2 D.2或-2或-
3.函数y=x+的图象是( )
4.已知函数f(x+1)=x2-2x+3,则函数y=f(x)的解析式为( )
A.f(x)=x2-6x+4 B.f(x)=x2-4x+6
C.f(x)=x2-4x-4 D.f(x)=x2-6x+11
5.已知函数f(x)是一次函数,且f[f(x)-4x]=5恒成立,则f(2)=( )
A.1 B.3 C.7 D.9
6.(多选)已知函数f(x)=若f(f(a))=2,则实数a的值为( )
A.-2 B.- C.-1 D.1
7.[2022·广东深圳高一期末]已知函数f(x)=,则f(f(5))=________.
8.已知函数f(x)满足f(x)+2f(-x)=2x+3,则f(x)=________.
9.已知函数f(x)=且f(2)=0.
(1)求f(f(1));
(2)若f(m)=-m,求实数m的值.
10.求下列函数的解析式.
(1)已知f(x)是一次函数,且满足3f(x+1)-2f(x-1)=2x+17,求f(x);
(2)若函数f()=x-1,求f(x).
核心素养升级练
1.(多选)具有性质f()=-f(x)的函数,我们称为满足“倒负”变换的函数,给出下列函数,其中满足“倒负”变换的函数是( )
A.f(x)=x- B.f(x)=x+
C.f(x)= D.f(x)=x2-
2.对于任意的实数x1、x2,min{x1,x2}表示x1、x2中较小的那个数.若函数f(x)=2-x2,g(x)=x,记h(x)=min{f(x),g(x)},则h(x)的解析式为________________.
3.已知函数f(x)=
(1)画出函数f(x)的图象;
(2)求f(f(3)),f(a2+1)(a∈R)的值;
(3)当f(x)≥2时,求x的取值范围.
3.1.2 函数的表示法
必备知识基础练
1.答案:A
解析:函数y=x-1为一次函数,图象为直线,但是当x≥0时,所得到的图象为一条射线.
2.答案:B
解析:观察函数y=g(x)的图象得:g(2)=1,由表格知:f(1)=2,所以f(g(2))=2.
3.答案:B
解析:设f(x)=(k≠0),
∵f(-3)==-1,∴k=3,
∴f(x)=.
4.答案:B
解析:根据题意,因为f(-1)=2,所以f(f(-1))=f(2)=.
5.答案:B
解析:g(f(2))=g(4)=2,g(f(3))=g(2)=4,g(f(4))=g(5)=4,g(f(5))=g(2)=4,所以所求值域是{2,4}.
6.答案:AD
解析:对于A:f(x)=,定义域为[1,5]∪(-∞,1)=(-∞,5],且[1,5]∩(-∞,1)= ,符合函数定义,且在定义域的不同区间,有不同的对应关系,故A正确;
对于B:f(x)=,定义域为R∪[2,+∞)=R,但R∩[2,+∞)=[2,+∞)≠ 不满足函数的定义,如当x=2时,f(2)=3和4,故不是函数,故B错误;
对于C:f(x)=,定义域为[1,5]∪(-∞,1]=(-∞,5],且[1,5]∩(-∞,1)={1},且f(1)=5和1,故不是函数,故C错误;
对于D:f(x)=,定义域为(-∞,0)∪[5,+∞),且(-∞,0)∩[5,+∞)= ,符合函数定义,且在定义域的不同区间,有不同的对应关系,故D正确.
7.答案:f(x)=-x2-4x-1
解析:根据顶点为(-2,3),设f(x)=a(x+2)2+3(a≠0),
由f(x)过点(-3,2),得2=a×1+3,
解得a=-1,
所以f(x)=-(x+2)2+3=-x2-4x-1.
8.答案:-
解析:令x=,则2x-1=0,所以f(0)=f(2×-1)=()2-2×=-.
关键能力综合练
1.答案:C
解析:由题意知:一开始岀发,心情轻松,缓慢行进,所以开始曲线比较平缓,后来发现时间比较紧,为了赶时间开始加速,所以曲线变得越来越陡峭,又因为纵轴表示离校的距离,横轴表示出发后的时间,所以开始距离最大,最后距离为0,故选C.
2.答案:A
解析:当x≤0时,f(x)=x2+1=5,解得:x=-2或x=2(舍),∴x=-2;
当x>0时,f(x)=-2x=5,解得:x=-(舍);
综上所述:x的值是-2.
3.答案:C
解析:对于y=x+,当x>0时,y=x+1;当x<0时,y=x-1.
即y=,故其图象应为C.
4.答案:B
解析:因为f(x+1)=x2-2x+3,
令t=x+1,则x=t-1,
则f(t)=(t-1)2-2(t-1)+3=t2-4t+6,
所以f(x)=x2-4x+6.
5.答案:D
解析:因为函数f(x)是一次函数,且f[f(x)-4x]=5恒成立,
令f(x)-4x=t,则f(x)=4x+t,
所以f(t)=4t+t=5,解得t=1,
所以f(x)=4x+1,f(2)=2×4+1=9.
6.答案:AB
解析:令f(a)=t,故f(t)=2,进而得t=-1或t=1,
所以f(a)=-1或f(a)=1,
由于x>0时,f(x)≥2,
所以3a+5=-1或3a+5=1,解得a=-2或a=-.
7.答案:1
解析:因为函数f(x)=,
所以f(5)=f(3)=f(1)=12=1,
所以f(f(5))=f(1)=12=1.
8.答案:-2x+1
解析:因为f(x)+2f(-x)=2x+3,①
所以f(-x)+2f(x)=2·(-x)+3,②
②×2-①得,f(x)=-2x+1.
9.解析:(1)∵f(2)=2a-1=0得a=,
∴f(x)=,
∴f(1)=-,
∴f(f(1))=f(-)=-2.
(2)当m≥0时,由f(m)=-m得m-1=-m解得m=;
当m<0时,由f(m)=-m得=-m,无实数解,
综上所述,m=.
10.解析:(1)因为f(x)是一次函数,设f(x)=ax+b,(a≠0),
则f(x+1)=a(x+1)+b,f(x-1)=a(x-1)+b,
所以3f(x+1)-2f(x-1)=ax+5a+b=2x+17,
则,解得,
所以f(x)=2x+7.
(2)由函数f()=x-1,
令=t≥0,则x=t2-1,
所以f(t)=t2-2,
所以f(x)=x2-2,x∈[0,+∞).
核心素养升级练
1.答案:AC
解析:对于选项A,f()=-x,-f(x)=-x,故满足“倒负”变换;
对于选项B,f()=+x,-f(x)=--x,故不满足“倒负”变换;
对于选项C,当0<x<1时,f()=-x,-f(x)=-x,当x=1时,f(1)=0,成立,当x>1时,f()=,-f(x)=,故满足“倒负”变换;
对于选项D,f()=,-f(x)=,故不满足“倒负”变换.
2.答案:h(x)=
解析:当f(x)≤g(x)时,即2-x2≤x,即x2+x-2≥0,解得x≤-2或x≥1,
此时,h(x)=min{f(x),g(x)}=f(x)=2-x2;
当f(x)>g(x)时,即2-x2>x,即x2+x-2<0,
解得-2
综上所述,h(x)=.
3.解析:(1)函数f(x)的图象如图所示:
(2)f(f(3))=f(3-32)=f(-6)=1-2×(-6)=13,
f(a2+1)=3-(a2+1)2=-a4-2a2+2;
(3)当x>0时,f(x)≥2 3-x2≥2 -1≤x≤1,∴0
当x<0时,f(x)≥2 1-2x≥2 x≤-,
综上所述:x的取值范围为:(-∞,-]∪[0,1].
1
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
