人教版数学八年级上册 12.2 三角形全等的判定(2)教案
文档属性
| 名称 | 人教版数学八年级上册 12.2 三角形全等的判定(2)教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 798.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 00:00:00 | ||
图片预览



文档简介
第十二章 全等三角形
12.2 全等三角形的判定
第2课时 利用两边及其夹角判定三角形全等(SAS)
一、教学目标
【知识与技能】
掌握“边角边”条件的内容,能初步应用“边角边”条件判定两个三角形全等.
【过程与方法】
经历探索三角形“边角边”判定定理的过程,在观察中寻求新知,在探索中发展推理能力,逐步掌握说理的基本方法.
【情感、态度与价值观】
通过探究三角形全等的条件的活动,培养学生观察分析图形的能力及运算能力,培养学生乐于探索的良好品质以及发现问题的能力.
二、课型
新授课
三、课时
第2课时,共4课时。
四、教学重难点
【教学重点】
会用“边角边”证明两个三角形全等,得到线段或角相等.
【教学难点】
指导学生分析问题,寻找判定三角形全等的条件.
五、课前准备
教师:课件、三角尺、直尺等。
学生:三角尺、直尺、剪刀。
六、教学过程
(一)导入新课
在上节课的讨论中,我们发现三角形中只给一个条件或两个条件时,都不能保证所画出的三角形一定全等.给出三个条件时,有四种可能,能说出是哪四种吗
问题:如图有一池塘.要测池塘两端A、B的距离,可无法直接到达,因此这两点的距离无法直接量出.你能想出办法来吗?
(出示课件2-3)
(二)探索新知
1.师生合作,探究三角形全等判定方法2
教师问1:我们学习了三角形全等的判定方法 1,请同学们回一下并回答其内容.
学生回答:三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”).
教师问2:用几何语言如何表示呢?
出示课件5:符号语言表达:
在△ABC和△ DEF中
AB=DE,
BC=EF,
CA=FD,
∴ △ABC ≌△ DEF.(SSS)
教师问3:除了SSS外,还有其他情况能判定两个三角形全等吗?当两个三角形满足六个条件中的3个时,有四种情况,还有哪一些呢?(出示课件6)
学生回答:两边一角和两角一边
教师问4:今天我们来探究一下两边一角的情况,已知一个三角形的两条边和一个角,那么这两条边与这一个角的位置上有几种可能性呢?
学生讨论并回答:有两种情况:两边及夹角和两边和其中一边的对角
学生问:它们能判定两个三角形全等吗?
教师我们还是通过画图来验证,我们先看两边及其夹角能否判定两个三角形全等,同学们根据下边的要求作图:
已知任意△ABC,画△A′B′C′,使A′B′=AB,A′C′=AC,∠A′=∠A.
分析:(1)作∠MB′N=∠B;
(2)在射线B′M上截取B′A′=AB,在射线B′N上截取B′C′=BC;
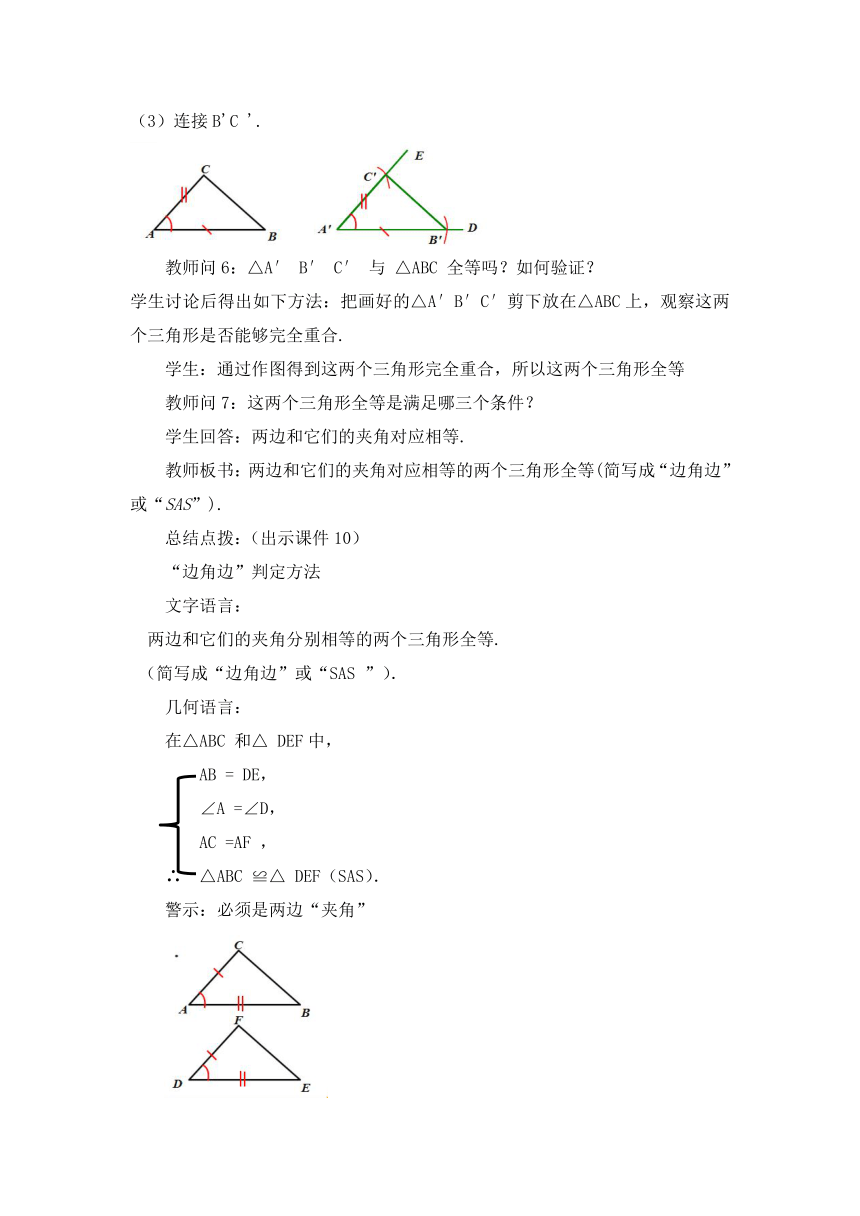
(3)连接B′C′.
教师问5:如何画呢?
学生讨论后回答,教师引导总结:
作法:
(出示课件9)(1)画∠DA'E=∠A;
(2)在射线A'D上截取A'B'=AB,在射线A'E上截取A'C'=AC;
(3)连接B'C '.
教师问6:△A′ B′ C′ 与 △ABC 全等吗?如何验证?
学生讨论后得出如下方法:把画好的△A′B′C′剪下放在△ABC上,观察这两个三角形是否能够完全重合.
学生:通过作图得到这两个三角形完全重合,所以这两个三角形全等
教师问7:这两个三角形全等是满足哪三个条件?
学生回答:两边和它们的夹角对应相等.
教师板书:两边和它们的夹角对应相等的两个三角形全等(简写成“边角边”或“SAS”).
总结点拨:(出示课件10)
“边角边”判定方法
文字语言:
两边和它们的夹角分别相等的两个三角形全等.
(简写成“边角边”或“SAS ”).
几何语言:
在△ABC 和△ DEF中,
AB = DE,
∠A =∠D,
AC =AF ,
∴ △ABC ≌△ DEF(SAS).
警示:必须是两边“夹角”
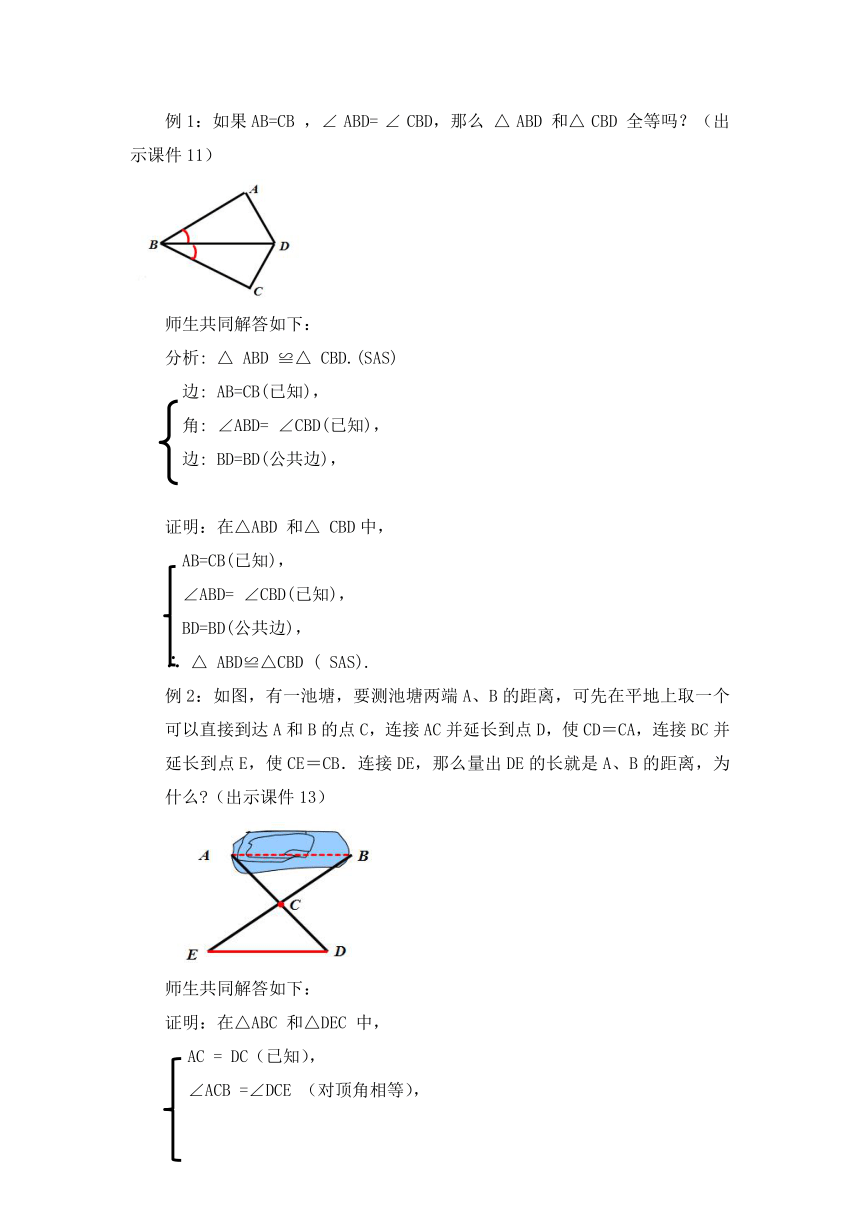
例1:如果AB=CB ,∠ ABD= ∠ CBD,那么 △ ABD 和△ CBD 全等吗?(出示课件11)
师生共同解答如下:
分析: △ ABD ≌△ CBD.(SAS)
边: AB=CB(已知),
角: ∠ABD= ∠CBD(已知),
边: BD=BD(公共边),
证明:在△ABD 和△ CBD中,
AB=CB(已知),
∠ABD= ∠CBD(已知),
BD=BD(公共边),
∴ △ ABD≌△CBD ( SAS).
例2:如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离,为什么 (出示课件13)
师生共同解答如下:
证明:在△ABC 和△DEC 中,
AC = DC(已知),
∠ACB =∠DCE (对顶角相等),
CB=EC(已知),
∴△ABC ≌△DEC(SAS).
∴AB =DE .(全等三角形的对应边相等)
2.展开想象,探究SSA能否判定两个三角形全等
教师问8:同学们想一下,两边一角还有那种情况呢?
学生回答:两边及其一边的对角
教师问9:已知两边及其一边的对角能否判定两个三角形全等?
学生小组讨论后,认为利用作图观察.
教师引导学生作图,提示学生考虑全面,然后给出下面的问题:(出示课件15)
如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC.固定住长木棍,转动短木棍,得到△ABD.这个实验说明了什么?
△ABC和△ABD满足AB=AB ,AC=AD,∠B=∠B,但△ABC与△ABD不全等.
教师问10:画△ABC 和△ABD,使∠A =∠A =30°, AB =AB=5 cm ,BC =BD =3 cm .观察所得的两个三角形是否全等?
学生作图并且比较后回答:不全等.
出示课件16:结论:两边和其中一边的对角分别相等的两个三角形不一定全等.
例3:下列条件中,不能证明△ABC≌△DEF的是( )(出示课件17)
A.AB=DE,∠B=∠E,BC=EF
B.AB=DE,∠A=∠D,AC=DF
C.BC=EF,∠B=∠E,AC=DF
D.BC=EF,∠C=∠F,AC=DF
师生共同解答如下:
解析:要判断能不能使△ABC≌△DEF,应看所给出的条件是不是两边和这两边的夹角,只有选项C的条件不符合,故选C.
总结点拨:判断三角形全等时,注意两边与其中一边的对角相等的两个三角形不一定全等.只有两边及夹角对应相等时,才能判定三角形全等.
(三)课堂练习(出示课件21-25)
1.在下列图中找出全等三角形进行连线.
2.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增加的条件是 ( )
A.∠A=∠D B.∠E=∠C
C.∠A=∠C D.∠ABD=∠EBC
3.如图,已知AC平分∠BAD, AB=AD.
求证:△ABC≌△ADC.
4. 已知:如图,AB=AC, BD=CD,E为AD上一点.
求证: BE=CE.
5. 如图,已知CA=CB , AD=BD, M,N分别是CA,CB的中点,求证:DM=DN.
参考答案:
1.答案如下:
2.D
3. 证明:∵AC平分∠BAD,
∴∠BAC=∠DAC,
在△ABC和△ADC中,
AD=AB (已知),
∠BAC=∠DAC (已证),
AC=AC (公共边),
∴△ABC≌△ADC(SAS).
4. 证明:在△ABD和△ACD中,
AB=AC (已知),
BD=CD (已知),
AD=AD(公共边),
∴△ABD≌△ACD(SSS).
∴ ∠BAD=∠CAD,
在△ABE和△ACE中,
AB=AC (已知),
∠BAD=∠CAD(已证),
AE=AE (公共边),
∴△ABE≌△ACE(SAS).
∴ BE=CE.
5. 证明: 连接CD,如图所示;
在△ABD与△CBD中
CA=CB, (已知)
AD=BD , (已知)
CD=CD ,(公共边)
∴△ACD≌△BCD(SSS)
∴∠A=∠B
又∵M,N分别是CA,CB的中点,
∴ AM=BN
在△AMD与△BND中
AM=BN ,(已证)
∠A=∠B ,(已证)
AD=BD ,(已知)
∴△AMD≌△BND.(SAS)
∴DM=DN.
(四)课堂小结
今天我们学了哪些内容:
1. 判定定理2:
两边及其夹角对应相等的两个三角形全等(简称为“边角边”或“SAS”).
2.利用SSA不能判定两个三角形全等
(五)课前预习
预习下节课(12.2)教材39页到41页的相关内容。
知道三角形全等的判定方法(角边角和角角边)
七、课后作业
1、教材39页练习1,2
2、如图,已知在△ABC中,AB=12,AC=8,AD是BC边上的中线,求AD的取值范围.
八、板书设计:
九、教学反思:
本节课的教学设计把学习中的发现、探究、研究等活动凸显出来,更多地由学生自己来发现问题、提出问题、分析和解决问题.通过学生参与探究,相互交流,突出学生是学习的主人,将课堂还给学生,体现学生的主体地位.抓住学生的好奇心,以疑激学,激起学生的求知欲,让学生主动建构、主动学习.同时,通过深入有效的评价,及时强化和矫正课程与教学的信息,更好地实现课程目的,提高教学质量,促进学生提高自我意识、自我调节、自我完善.
12.2 全等三角形的判定
第2课时 利用两边及其夹角判定三角形全等(SAS)
一、教学目标
【知识与技能】
掌握“边角边”条件的内容,能初步应用“边角边”条件判定两个三角形全等.
【过程与方法】
经历探索三角形“边角边”判定定理的过程,在观察中寻求新知,在探索中发展推理能力,逐步掌握说理的基本方法.
【情感、态度与价值观】
通过探究三角形全等的条件的活动,培养学生观察分析图形的能力及运算能力,培养学生乐于探索的良好品质以及发现问题的能力.
二、课型
新授课
三、课时
第2课时,共4课时。
四、教学重难点
【教学重点】
会用“边角边”证明两个三角形全等,得到线段或角相等.
【教学难点】
指导学生分析问题,寻找判定三角形全等的条件.
五、课前准备
教师:课件、三角尺、直尺等。
学生:三角尺、直尺、剪刀。
六、教学过程
(一)导入新课
在上节课的讨论中,我们发现三角形中只给一个条件或两个条件时,都不能保证所画出的三角形一定全等.给出三个条件时,有四种可能,能说出是哪四种吗
问题:如图有一池塘.要测池塘两端A、B的距离,可无法直接到达,因此这两点的距离无法直接量出.你能想出办法来吗?
(出示课件2-3)
(二)探索新知
1.师生合作,探究三角形全等判定方法2
教师问1:我们学习了三角形全等的判定方法 1,请同学们回一下并回答其内容.
学生回答:三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”).
教师问2:用几何语言如何表示呢?
出示课件5:符号语言表达:
在△ABC和△ DEF中
AB=DE,
BC=EF,
CA=FD,
∴ △ABC ≌△ DEF.(SSS)
教师问3:除了SSS外,还有其他情况能判定两个三角形全等吗?当两个三角形满足六个条件中的3个时,有四种情况,还有哪一些呢?(出示课件6)
学生回答:两边一角和两角一边
教师问4:今天我们来探究一下两边一角的情况,已知一个三角形的两条边和一个角,那么这两条边与这一个角的位置上有几种可能性呢?
学生讨论并回答:有两种情况:两边及夹角和两边和其中一边的对角
学生问:它们能判定两个三角形全等吗?
教师我们还是通过画图来验证,我们先看两边及其夹角能否判定两个三角形全等,同学们根据下边的要求作图:
已知任意△ABC,画△A′B′C′,使A′B′=AB,A′C′=AC,∠A′=∠A.
分析:(1)作∠MB′N=∠B;
(2)在射线B′M上截取B′A′=AB,在射线B′N上截取B′C′=BC;
(3)连接B′C′.
教师问5:如何画呢?
学生讨论后回答,教师引导总结:
作法:
(出示课件9)(1)画∠DA'E=∠A;
(2)在射线A'D上截取A'B'=AB,在射线A'E上截取A'C'=AC;
(3)连接B'C '.
教师问6:△A′ B′ C′ 与 △ABC 全等吗?如何验证?
学生讨论后得出如下方法:把画好的△A′B′C′剪下放在△ABC上,观察这两个三角形是否能够完全重合.
学生:通过作图得到这两个三角形完全重合,所以这两个三角形全等
教师问7:这两个三角形全等是满足哪三个条件?
学生回答:两边和它们的夹角对应相等.
教师板书:两边和它们的夹角对应相等的两个三角形全等(简写成“边角边”或“SAS”).
总结点拨:(出示课件10)
“边角边”判定方法
文字语言:
两边和它们的夹角分别相等的两个三角形全等.
(简写成“边角边”或“SAS ”).
几何语言:
在△ABC 和△ DEF中,
AB = DE,
∠A =∠D,
AC =AF ,
∴ △ABC ≌△ DEF(SAS).
警示:必须是两边“夹角”
例1:如果AB=CB ,∠ ABD= ∠ CBD,那么 △ ABD 和△ CBD 全等吗?(出示课件11)
师生共同解答如下:
分析: △ ABD ≌△ CBD.(SAS)
边: AB=CB(已知),
角: ∠ABD= ∠CBD(已知),
边: BD=BD(公共边),
证明:在△ABD 和△ CBD中,
AB=CB(已知),
∠ABD= ∠CBD(已知),
BD=BD(公共边),
∴ △ ABD≌△CBD ( SAS).
例2:如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离,为什么 (出示课件13)
师生共同解答如下:
证明:在△ABC 和△DEC 中,
AC = DC(已知),
∠ACB =∠DCE (对顶角相等),
CB=EC(已知),
∴△ABC ≌△DEC(SAS).
∴AB =DE .(全等三角形的对应边相等)
2.展开想象,探究SSA能否判定两个三角形全等
教师问8:同学们想一下,两边一角还有那种情况呢?
学生回答:两边及其一边的对角
教师问9:已知两边及其一边的对角能否判定两个三角形全等?
学生小组讨论后,认为利用作图观察.
教师引导学生作图,提示学生考虑全面,然后给出下面的问题:(出示课件15)
如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC.固定住长木棍,转动短木棍,得到△ABD.这个实验说明了什么?
△ABC和△ABD满足AB=AB ,AC=AD,∠B=∠B,但△ABC与△ABD不全等.
教师问10:画△ABC 和△ABD,使∠A =∠A =30°, AB =AB=5 cm ,BC =BD =3 cm .观察所得的两个三角形是否全等?
学生作图并且比较后回答:不全等.
出示课件16:结论:两边和其中一边的对角分别相等的两个三角形不一定全等.
例3:下列条件中,不能证明△ABC≌△DEF的是( )(出示课件17)
A.AB=DE,∠B=∠E,BC=EF
B.AB=DE,∠A=∠D,AC=DF
C.BC=EF,∠B=∠E,AC=DF
D.BC=EF,∠C=∠F,AC=DF
师生共同解答如下:
解析:要判断能不能使△ABC≌△DEF,应看所给出的条件是不是两边和这两边的夹角,只有选项C的条件不符合,故选C.
总结点拨:判断三角形全等时,注意两边与其中一边的对角相等的两个三角形不一定全等.只有两边及夹角对应相等时,才能判定三角形全等.
(三)课堂练习(出示课件21-25)
1.在下列图中找出全等三角形进行连线.
2.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增加的条件是 ( )
A.∠A=∠D B.∠E=∠C
C.∠A=∠C D.∠ABD=∠EBC
3.如图,已知AC平分∠BAD, AB=AD.
求证:△ABC≌△ADC.
4. 已知:如图,AB=AC, BD=CD,E为AD上一点.
求证: BE=CE.
5. 如图,已知CA=CB , AD=BD, M,N分别是CA,CB的中点,求证:DM=DN.
参考答案:
1.答案如下:
2.D
3. 证明:∵AC平分∠BAD,
∴∠BAC=∠DAC,
在△ABC和△ADC中,
AD=AB (已知),
∠BAC=∠DAC (已证),
AC=AC (公共边),
∴△ABC≌△ADC(SAS).
4. 证明:在△ABD和△ACD中,
AB=AC (已知),
BD=CD (已知),
AD=AD(公共边),
∴△ABD≌△ACD(SSS).
∴ ∠BAD=∠CAD,
在△ABE和△ACE中,
AB=AC (已知),
∠BAD=∠CAD(已证),
AE=AE (公共边),
∴△ABE≌△ACE(SAS).
∴ BE=CE.
5. 证明: 连接CD,如图所示;
在△ABD与△CBD中
CA=CB, (已知)
AD=BD , (已知)
CD=CD ,(公共边)
∴△ACD≌△BCD(SSS)
∴∠A=∠B
又∵M,N分别是CA,CB的中点,
∴ AM=BN
在△AMD与△BND中
AM=BN ,(已证)
∠A=∠B ,(已证)
AD=BD ,(已知)
∴△AMD≌△BND.(SAS)
∴DM=DN.
(四)课堂小结
今天我们学了哪些内容:
1. 判定定理2:
两边及其夹角对应相等的两个三角形全等(简称为“边角边”或“SAS”).
2.利用SSA不能判定两个三角形全等
(五)课前预习
预习下节课(12.2)教材39页到41页的相关内容。
知道三角形全等的判定方法(角边角和角角边)
七、课后作业
1、教材39页练习1,2
2、如图,已知在△ABC中,AB=12,AC=8,AD是BC边上的中线,求AD的取值范围.
八、板书设计:
九、教学反思:
本节课的教学设计把学习中的发现、探究、研究等活动凸显出来,更多地由学生自己来发现问题、提出问题、分析和解决问题.通过学生参与探究,相互交流,突出学生是学习的主人,将课堂还给学生,体现学生的主体地位.抓住学生的好奇心,以疑激学,激起学生的求知欲,让学生主动建构、主动学习.同时,通过深入有效的评价,及时强化和矫正课程与教学的信息,更好地实现课程目的,提高教学质量,促进学生提高自我意识、自我调节、自我完善.
