高中数学人教A版(2019)必修第一册3.4函数的应用(一)(能力篇)(有解析 )
文档属性
| 名称 | 高中数学人教A版(2019)必修第一册3.4函数的应用(一)(能力篇)(有解析 ) | 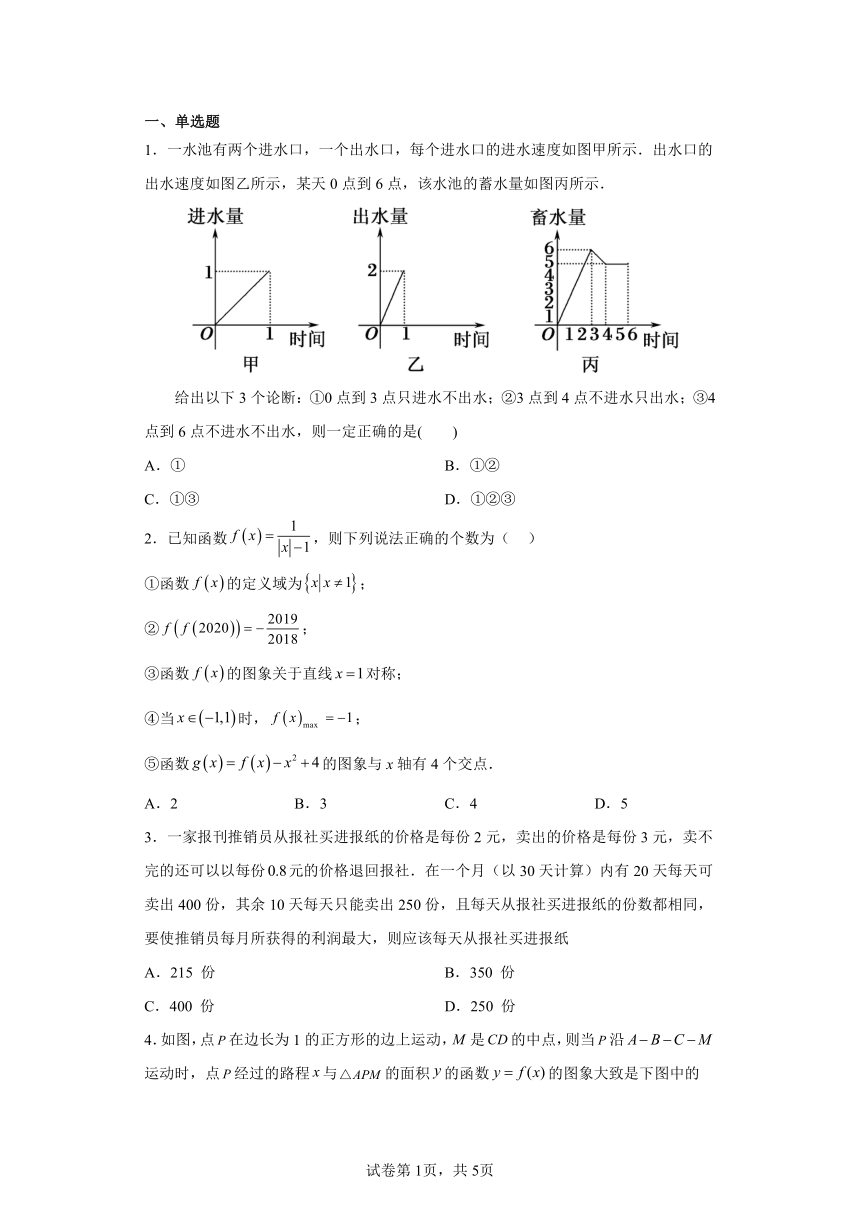 | |
| 格式 | docx | ||
| 文件大小 | 649.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 13:00:57 | ||
图片预览





文档简介
一、单选题
1.一水池有两个进水口,一个出水口,每个进水口的进水速度如图甲所示.出水口的出水速度如图乙所示,某天0点到6点,该水池的蓄水量如图丙所示.
给出以下3个论断:①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点不进水不出水,则一定正确的是( )
A.① B.①②
C.①③ D.①②③
2.已知函数,则下列说法正确的个数为( )
①函数的定义域为;
②;
③函数的图象关于直线对称;
④当时,;
⑤函数的图象与x轴有4个交点.
A.2 B.3 C.4 D.5
3.一家报刊推销员从报社买进报纸的价格是每份2元,卖出的价格是每份3元,卖不完的还可以以每份元的价格退回报社.在一个月(以30天计算)内有20天每天可卖出400份,其余10天每天只能卖出250份,且每天从报社买进报纸的份数都相同,要使推销员每月所获得的利润最大,则应该每天从报社买进报纸
A.215 份 B.350 份
C.400 份 D.250 份
4.如图,点在边长为1的正方形的边上运动,是的中点,则当沿运动时,点经过的路程与的面积的函数的图象大致是下图中的
A. B.
C. D.
5.设函数,则满足的x的取值范围是( )
A. B. C. D.
6.周末,自行车骑行爱好者甲、乙两人相约沿同一路线从地出发前往地进行骑行训练,甲、乙分别以不同的速度匀速骑行,乙比甲早出发分钟.乙骑行分钟后,甲以原速的继续骑行,经过一段时间,甲先到达地,乙一直保持原速前往地.在此过程中,甲、乙两人相距的路程(单位:米)与乙骑行的时间(单位:分钟)之间的关系如图所示,则下列说法错误的是( )
A.乙的速度为米/分钟 B.分钟后甲的速度为米/分钟
C.乙比甲晚分钟到达地 D.、两地之间的路程为米
二、多选题
7.记实数中的最大数为,最小数为,则关于函数的说法中正确的是( )
A.方程有三个根 B.的单调减区间为和
C.的最大值为 D.的最小值为
8.甲乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中甲因故障停止一会后又继续按原速加工,直到他们完成任务.如图表示甲比乙多加工的零件数量(个)与加工时间(分)之间的函数关系,点横坐标为12,点坐标为点横坐标为128.则下面说法中正确的是( )
A.甲每分钟加工的零件数量是5个 B.在60分钟时,甲比乙多加工了120个零件
C.点的横坐标是200 D.的最大值是216
三、填空题
9.把长为12cm的细铁丝锯成两段,各自围成一个正三角形,那么这两个正三角形最小的面积之和是________.
10.若正数,,满足,则的最大值是________.
11.已知函数若关于的方程有5个不同的实数根,则的取值范围为___________.
12.某公司生产某种产品,固定成本为20000元,每生产一单位产品,成本增加100元,已知总收益与年产量的关系式,则总利润最大时,每年生产的产品数量是__________.
四、解答题
13.某汽车公司购买了辆大客车用于长途客运,每辆万元,预计每辆客车每年收入约万元,每辆客车第一年各种费用约为万元,从第二年开始每年比上一年所需费用要增加万元.
(1)写出辆客车运营的总利润(万元)与运营年数的函数关系式:
(2)这辆客车运营多少年,可使年平均运营利润最大?最大利润是多少?
14.2022年第24届北京冬季奥林匹克运动会,于2022年2月4日星期五开幕,将于2月20日星期日闭幕.该奥运会激发了大家对冰雪运动的热情,与冰雪运动有关的商品销量持续增长.对某店铺某款冰雪运动装备在过去的一个月内(以30天计)的销售情况进行调查发现:该款冰雪运动装备的日销售单价(元/套)与时间x(被调查的一个月内的第x天)的函数关系近似满足(k为正常数).该商品的日销售量(个)与时间x(天)部分数据如下表所示:
x 10 20 25 30
110 120 125 120
已知第10天该商品的日销售收入为121元.
(1)求k的值;
(2)给出两种函数模型:①,②,请你根据上表中的数据,从中选择你认为最合适的一种函数来描述该商品的日销售量与时间x的关系,并求出该函数的解析式;
(3)求该商品的日销售收入(,)(元)的最小值.
15.为鼓励大学毕业生自主创业,某市出台了相关政策,由政府协调,企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.某大学毕业生校照相关政策投资销售一种新型节能灯,已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月的销售量(单位:件)与销售单价(单位:元)之间的关系近似满足一次函数: .
(1)设他每月获得的利润为 (单位:元),写出他每月获得的利润与销售单价x的函数关系式,并求出利润的最大值.
(2)相关部门规定,这种节能灯的销售单价不得高于元.如果他想要每月获得的利润不少于元,那么政府每个月为他承担的总差价的取值范围是多少
16.已知函数,方程在上有实根,求实数a的取值范围.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】由甲,乙图得进水速度1,出水速度2,结合丙图中直线的斜率解答.
【详解】由甲、乙两图可知进水速度为1,出水速度为2,结合丙图中直线的斜率,只进水不出水时,蓄水量增加速度是2,故①正确;不进水只出水时,蓄水量减少速度是2,故②不正确;两个进水一个出水时,蓄水量减少速度也是0,故③不正确.
【点睛】数形结合是解决此题的关键,本题关键是抓住斜率为解题的突破口.
2.B
【分析】根据分母不等于0,求解函数的定义域,判断①;代入验证判断②;画出函数的图象,判断④⑤;画出函数和的图象,即可判断函数图象的交点个数.
【详解】函数的定义域为,故①错误;
,故②正确;
作出的图象如图所示,由图可知③错误,④正确.
令,得方程,
在上图中作出抛物线,由图可知的图象与抛物线有4个交点,
故函数的图象与轴有4个交点,故⑤正确.
故选:B.
3.C
【分析】设每天从报社买进份报纸时,根据题意求得函数的解析式,结合一次函数的性质,即可求解.
【详解】设每天从报社买进(,)份报纸时,每月所获利润为元,具体情况如下表.
数量/份 单价/元 金额/元
买进 2
卖出 3
退回
则推销员每月所获得的利润
又由在上单调递增,
所以当时,取得最大值8700.
故选C.
即每天从报社买进400份报纸时,每月获得的利润最大,最大利润为8700元.故选C.
【点睛】本题主要考查了函数的实际应用问题,其中解答中认真审题,列出函数的解析式,结合一次函数的单调性求解是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.
4.A
【分析】先分点在上时,点在上时,点在上时求得函数,再利用函数的性质来判断.
【详解】当点在上时:
当点在上时:
当点在上时:
由函数可知,有三段直线,又当点在上时是减函数
故选:A
【点睛】本题主要考查了分段函数的图象和性质,还考查了运算求解的能力,属于中档题.
5.D
【解析】由已知得出函数的单调性,利用其单调性建立不等式组,可得选项.
【详解】∵函数在上单调递减,在上为常数1,
所以由得,解得.
故选:D.
【点睛】本题考查分段函数的不等式求解问题,关键在于得出分段函数的单调性,属于中档题.
6.C
【分析】首先由图象确定甲乙两人的速度,再求出甲到达地时乙距离的的距离,计算甲的总路程即为、两地之间的路程,进而可判断各个选项的正确性,即可得正确答案.
【详解】因为乙比甲早出发分钟,由图知:乙的速度为米/分钟,故选项A正确;
设甲的原速度为,因为,解得:米/分钟,
所以分钟后甲的速度为米/分钟,故选项B正确;
当时,甲到达地,此时乙距离地还有米,所以还需要分钟,所以乙比甲晚分钟到达地,故选项C
不正确;
、两地之间的路程为米,故选项D正确;
所以说法错误的是选项C,
故选:C.
7.AC
【分析】由的定义可得图象,结合图象依次判断各个选项即可.
【详解】由的含义可得图象如下图所示,
由图象可知:
对于A,与有且仅有三个不同交点,即有三个根,A正确;
对于B,的单调递减区间为和,B错误;
对于C,,C正确;
对于D,无最小值,D错误.
故选:AC.
8.ACD
【分析】甲每分钟加工的数量是,所以选项A正确;在60分钟时,甲比乙多加工了(60-20)个零件,所以选项B错误;设的坐标为,由题得,则有,解可得,所以选项C正确;当时,,所以的最大值是216.所以选项D正确.
【详解】根据题意,甲一共加工的时间为分钟,
一共加工了600个零件,则甲每分钟加工的数量是,所以选项A正确,
设的坐标为,
在区间和,20 上,都是乙在加工,则直线和的斜率相等,
则有,
在区间和上,甲乙同时加工,同理可得,
则,
则有,解可得;
即点的坐标是,所以选项C正确;
由题得乙每分钟加工的零件数为个,
所以甲每分钟比乙多加工5-3=2个,
在60分钟时,甲比乙多加工了(60-20)个零件,所以选项B错误;
当时,,所以的最大值是216.所以选项D正确.
故选:ACD
9.2 cm2.
【详解】试题分析:设一个三角形的边长为x cm,则另一个三角形的边长为(4﹣x)cm,则可得到这两个正三角形面积之和,利用二次函数的性质求出其最小值.
解:设一个三角形的边长为x cm,则另一个三角形的边长为(4﹣x)cm,两个三角形的面积和为
S=x2+(4﹣x)2=x2﹣2x+4.
令S′=x﹣2=0,则x=2,所以Smin=2.
故答案为2 cm2.
点评:本题考查等边三角形的面积的求法,二次函数的性质及最小值的求法.
10.
【分析】将看成关于的方程,则问题等价于关于的方程有解,则,再将问题转化为关于的不等式有解,从而,进而得到结果.
【详解】解:把式子看作是关于的方程,则问题等价于关于的方程有解,则,即,则问题转化为关于的不等式有解,则,化简得,所以,此时,,符合条件.
故答案为:
【点睛】本题考查函数与方程,注意转化思想在解题中的应用,属于中档题.
11.
【分析】根据函数的解析式作出函数的大致图像,再将
整理变形,然后将方程的根的问题转化为函数图象的交点问题解决.
【详解】由题意得,即或,
的图象如图所示,
关于的方程有5个不同的实数根,
则或,解得,
故答案为:
12.300
【分析】利用总收益与成本的差可得总利润关于的解析式,利用分段函数的性质,分别求出两段函数的最值,从而可得结果.
【详解】设总成本为元,总利润为元,则,
P=R-C=所以=
令,得=300.当0< <300时,;当>300时,.所以当=300时,取得最大值.
故答案为:300.
13.(1);(2)这4辆客车运营年,可使年平均运营利润最大,最大利润为48万元.
【分析】(1)由题知,每辆车年总收入为万元,总支出为,进而得利润的表达式;
(2)结合(1)得年平均运营利润为,再根据基本不等式求解即可得答案.
【详解】解:(1)依题意得,每辆车年总收入为万元,
总支出为,
所以辆客车运营的总利润.
(2)年平均运营利润为,
因为,所以,当且仅当时,等号成立,
此时,
所以这4辆客车运营年,可使年平均运营利润最大,最大利润为48万元.
14.(1)
(2)选择②,,(,)
(3)121元
【分析】(1)根据第10天该商品的日销售收入为121元,列式求得答案;
(2)由表中数据的变化可确定描述该商品的日销售量与时间x的关系,代入表述数据可求得其解析式;
(3)讨论去掉绝对值符号,分段求出函数的最小值,比较可得答案.
(1)
因为第10天该商品的日销售收入为121元,
所以,解得;
(2)
由表中数据可得,当时间变化时,该商品的日销售量有增有减,并不单调,
故只能选②:
代入数据可得:,解得,,
所以,(,)
(3)
由(2)可得,,
所以,,
所以当,时,在区间上单调递减,在区间上单调递增,
所以当时,有最小值,且为121;
当,时,为单调递减函数,
所以当时,有最小值,且为124,
综上,当时,有最小值,且为121元,
所以该商品的日销售收入最小值为121元.
15.(1),;(2).
【分析】(1)每件的销售利润乘以每月的销售量即为利润,利用二次函数的性质即可求最值;
(2)令可得的范围,设政府每个月为他承担的总差价为元,由一次函数的性质即可求差价的取值范围.
【详解】(1)依题意可得:每件的销售利润为元,每月的销售量为件,
所以每月获得的利润与销售单价x的函数关系式为:
,
对称轴为,开口向下,此时最大值为,
所以利润与销售单价x的函数关系式,最大利润为元.
(2)由每月获得的利润不小于元,
得,
即 ,解得:,
这种节能灯的销售单价不得高于元,所以,
设政府每个月为他承担的总差价为元,
则,
由可得,
所以政府每个月为他承担的总差价的取值范围是元.
16..
【分析】根据题意,求得,根据二次函数的性质结合零点存在性定理,列出不等式,则问题得解.
【详解】因为,
①当时,根据零点存在性定理,显然在区间有根,
即,解得;
②当时,即时,此时,有,舍去;
③当时,即时,此时,有或,舍去,
④当时,即时,此时在上有两个实根,
显然不等式无解.
综上所述:.
【点睛】本题考查根据一元二次方程根的分布求参数范围,属中档题.
答案第1页,共2页
答案第1页,共2页
1.一水池有两个进水口,一个出水口,每个进水口的进水速度如图甲所示.出水口的出水速度如图乙所示,某天0点到6点,该水池的蓄水量如图丙所示.
给出以下3个论断:①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点不进水不出水,则一定正确的是( )
A.① B.①②
C.①③ D.①②③
2.已知函数,则下列说法正确的个数为( )
①函数的定义域为;
②;
③函数的图象关于直线对称;
④当时,;
⑤函数的图象与x轴有4个交点.
A.2 B.3 C.4 D.5
3.一家报刊推销员从报社买进报纸的价格是每份2元,卖出的价格是每份3元,卖不完的还可以以每份元的价格退回报社.在一个月(以30天计算)内有20天每天可卖出400份,其余10天每天只能卖出250份,且每天从报社买进报纸的份数都相同,要使推销员每月所获得的利润最大,则应该每天从报社买进报纸
A.215 份 B.350 份
C.400 份 D.250 份
4.如图,点在边长为1的正方形的边上运动,是的中点,则当沿运动时,点经过的路程与的面积的函数的图象大致是下图中的
A. B.
C. D.
5.设函数,则满足的x的取值范围是( )
A. B. C. D.
6.周末,自行车骑行爱好者甲、乙两人相约沿同一路线从地出发前往地进行骑行训练,甲、乙分别以不同的速度匀速骑行,乙比甲早出发分钟.乙骑行分钟后,甲以原速的继续骑行,经过一段时间,甲先到达地,乙一直保持原速前往地.在此过程中,甲、乙两人相距的路程(单位:米)与乙骑行的时间(单位:分钟)之间的关系如图所示,则下列说法错误的是( )
A.乙的速度为米/分钟 B.分钟后甲的速度为米/分钟
C.乙比甲晚分钟到达地 D.、两地之间的路程为米
二、多选题
7.记实数中的最大数为,最小数为,则关于函数的说法中正确的是( )
A.方程有三个根 B.的单调减区间为和
C.的最大值为 D.的最小值为
8.甲乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中甲因故障停止一会后又继续按原速加工,直到他们完成任务.如图表示甲比乙多加工的零件数量(个)与加工时间(分)之间的函数关系,点横坐标为12,点坐标为点横坐标为128.则下面说法中正确的是( )
A.甲每分钟加工的零件数量是5个 B.在60分钟时,甲比乙多加工了120个零件
C.点的横坐标是200 D.的最大值是216
三、填空题
9.把长为12cm的细铁丝锯成两段,各自围成一个正三角形,那么这两个正三角形最小的面积之和是________.
10.若正数,,满足,则的最大值是________.
11.已知函数若关于的方程有5个不同的实数根,则的取值范围为___________.
12.某公司生产某种产品,固定成本为20000元,每生产一单位产品,成本增加100元,已知总收益与年产量的关系式,则总利润最大时,每年生产的产品数量是__________.
四、解答题
13.某汽车公司购买了辆大客车用于长途客运,每辆万元,预计每辆客车每年收入约万元,每辆客车第一年各种费用约为万元,从第二年开始每年比上一年所需费用要增加万元.
(1)写出辆客车运营的总利润(万元)与运营年数的函数关系式:
(2)这辆客车运营多少年,可使年平均运营利润最大?最大利润是多少?
14.2022年第24届北京冬季奥林匹克运动会,于2022年2月4日星期五开幕,将于2月20日星期日闭幕.该奥运会激发了大家对冰雪运动的热情,与冰雪运动有关的商品销量持续增长.对某店铺某款冰雪运动装备在过去的一个月内(以30天计)的销售情况进行调查发现:该款冰雪运动装备的日销售单价(元/套)与时间x(被调查的一个月内的第x天)的函数关系近似满足(k为正常数).该商品的日销售量(个)与时间x(天)部分数据如下表所示:
x 10 20 25 30
110 120 125 120
已知第10天该商品的日销售收入为121元.
(1)求k的值;
(2)给出两种函数模型:①,②,请你根据上表中的数据,从中选择你认为最合适的一种函数来描述该商品的日销售量与时间x的关系,并求出该函数的解析式;
(3)求该商品的日销售收入(,)(元)的最小值.
15.为鼓励大学毕业生自主创业,某市出台了相关政策,由政府协调,企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.某大学毕业生校照相关政策投资销售一种新型节能灯,已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月的销售量(单位:件)与销售单价(单位:元)之间的关系近似满足一次函数: .
(1)设他每月获得的利润为 (单位:元),写出他每月获得的利润与销售单价x的函数关系式,并求出利润的最大值.
(2)相关部门规定,这种节能灯的销售单价不得高于元.如果他想要每月获得的利润不少于元,那么政府每个月为他承担的总差价的取值范围是多少
16.已知函数,方程在上有实根,求实数a的取值范围.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】由甲,乙图得进水速度1,出水速度2,结合丙图中直线的斜率解答.
【详解】由甲、乙两图可知进水速度为1,出水速度为2,结合丙图中直线的斜率,只进水不出水时,蓄水量增加速度是2,故①正确;不进水只出水时,蓄水量减少速度是2,故②不正确;两个进水一个出水时,蓄水量减少速度也是0,故③不正确.
【点睛】数形结合是解决此题的关键,本题关键是抓住斜率为解题的突破口.
2.B
【分析】根据分母不等于0,求解函数的定义域,判断①;代入验证判断②;画出函数的图象,判断④⑤;画出函数和的图象,即可判断函数图象的交点个数.
【详解】函数的定义域为,故①错误;
,故②正确;
作出的图象如图所示,由图可知③错误,④正确.
令,得方程,
在上图中作出抛物线,由图可知的图象与抛物线有4个交点,
故函数的图象与轴有4个交点,故⑤正确.
故选:B.
3.C
【分析】设每天从报社买进份报纸时,根据题意求得函数的解析式,结合一次函数的性质,即可求解.
【详解】设每天从报社买进(,)份报纸时,每月所获利润为元,具体情况如下表.
数量/份 单价/元 金额/元
买进 2
卖出 3
退回
则推销员每月所获得的利润
又由在上单调递增,
所以当时,取得最大值8700.
故选C.
即每天从报社买进400份报纸时,每月获得的利润最大,最大利润为8700元.故选C.
【点睛】本题主要考查了函数的实际应用问题,其中解答中认真审题,列出函数的解析式,结合一次函数的单调性求解是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.
4.A
【分析】先分点在上时,点在上时,点在上时求得函数,再利用函数的性质来判断.
【详解】当点在上时:
当点在上时:
当点在上时:
由函数可知,有三段直线,又当点在上时是减函数
故选:A
【点睛】本题主要考查了分段函数的图象和性质,还考查了运算求解的能力,属于中档题.
5.D
【解析】由已知得出函数的单调性,利用其单调性建立不等式组,可得选项.
【详解】∵函数在上单调递减,在上为常数1,
所以由得,解得.
故选:D.
【点睛】本题考查分段函数的不等式求解问题,关键在于得出分段函数的单调性,属于中档题.
6.C
【分析】首先由图象确定甲乙两人的速度,再求出甲到达地时乙距离的的距离,计算甲的总路程即为、两地之间的路程,进而可判断各个选项的正确性,即可得正确答案.
【详解】因为乙比甲早出发分钟,由图知:乙的速度为米/分钟,故选项A正确;
设甲的原速度为,因为,解得:米/分钟,
所以分钟后甲的速度为米/分钟,故选项B正确;
当时,甲到达地,此时乙距离地还有米,所以还需要分钟,所以乙比甲晚分钟到达地,故选项C
不正确;
、两地之间的路程为米,故选项D正确;
所以说法错误的是选项C,
故选:C.
7.AC
【分析】由的定义可得图象,结合图象依次判断各个选项即可.
【详解】由的含义可得图象如下图所示,
由图象可知:
对于A,与有且仅有三个不同交点,即有三个根,A正确;
对于B,的单调递减区间为和,B错误;
对于C,,C正确;
对于D,无最小值,D错误.
故选:AC.
8.ACD
【分析】甲每分钟加工的数量是,所以选项A正确;在60分钟时,甲比乙多加工了(60-20)个零件,所以选项B错误;设的坐标为,由题得,则有,解可得,所以选项C正确;当时,,所以的最大值是216.所以选项D正确.
【详解】根据题意,甲一共加工的时间为分钟,
一共加工了600个零件,则甲每分钟加工的数量是,所以选项A正确,
设的坐标为,
在区间和,20 上,都是乙在加工,则直线和的斜率相等,
则有,
在区间和上,甲乙同时加工,同理可得,
则,
则有,解可得;
即点的坐标是,所以选项C正确;
由题得乙每分钟加工的零件数为个,
所以甲每分钟比乙多加工5-3=2个,
在60分钟时,甲比乙多加工了(60-20)个零件,所以选项B错误;
当时,,所以的最大值是216.所以选项D正确.
故选:ACD
9.2 cm2.
【详解】试题分析:设一个三角形的边长为x cm,则另一个三角形的边长为(4﹣x)cm,则可得到这两个正三角形面积之和,利用二次函数的性质求出其最小值.
解:设一个三角形的边长为x cm,则另一个三角形的边长为(4﹣x)cm,两个三角形的面积和为
S=x2+(4﹣x)2=x2﹣2x+4.
令S′=x﹣2=0,则x=2,所以Smin=2.
故答案为2 cm2.
点评:本题考查等边三角形的面积的求法,二次函数的性质及最小值的求法.
10.
【分析】将看成关于的方程,则问题等价于关于的方程有解,则,再将问题转化为关于的不等式有解,从而,进而得到结果.
【详解】解:把式子看作是关于的方程,则问题等价于关于的方程有解,则,即,则问题转化为关于的不等式有解,则,化简得,所以,此时,,符合条件.
故答案为:
【点睛】本题考查函数与方程,注意转化思想在解题中的应用,属于中档题.
11.
【分析】根据函数的解析式作出函数的大致图像,再将
整理变形,然后将方程的根的问题转化为函数图象的交点问题解决.
【详解】由题意得,即或,
的图象如图所示,
关于的方程有5个不同的实数根,
则或,解得,
故答案为:
12.300
【分析】利用总收益与成本的差可得总利润关于的解析式,利用分段函数的性质,分别求出两段函数的最值,从而可得结果.
【详解】设总成本为元,总利润为元,则,
P=R-C=所以=
令,得=300.当0< <300时,;当>300时,.所以当=300时,取得最大值.
故答案为:300.
13.(1);(2)这4辆客车运营年,可使年平均运营利润最大,最大利润为48万元.
【分析】(1)由题知,每辆车年总收入为万元,总支出为,进而得利润的表达式;
(2)结合(1)得年平均运营利润为,再根据基本不等式求解即可得答案.
【详解】解:(1)依题意得,每辆车年总收入为万元,
总支出为,
所以辆客车运营的总利润.
(2)年平均运营利润为,
因为,所以,当且仅当时,等号成立,
此时,
所以这4辆客车运营年,可使年平均运营利润最大,最大利润为48万元.
14.(1)
(2)选择②,,(,)
(3)121元
【分析】(1)根据第10天该商品的日销售收入为121元,列式求得答案;
(2)由表中数据的变化可确定描述该商品的日销售量与时间x的关系,代入表述数据可求得其解析式;
(3)讨论去掉绝对值符号,分段求出函数的最小值,比较可得答案.
(1)
因为第10天该商品的日销售收入为121元,
所以,解得;
(2)
由表中数据可得,当时间变化时,该商品的日销售量有增有减,并不单调,
故只能选②:
代入数据可得:,解得,,
所以,(,)
(3)
由(2)可得,,
所以,,
所以当,时,在区间上单调递减,在区间上单调递增,
所以当时,有最小值,且为121;
当,时,为单调递减函数,
所以当时,有最小值,且为124,
综上,当时,有最小值,且为121元,
所以该商品的日销售收入最小值为121元.
15.(1),;(2).
【分析】(1)每件的销售利润乘以每月的销售量即为利润,利用二次函数的性质即可求最值;
(2)令可得的范围,设政府每个月为他承担的总差价为元,由一次函数的性质即可求差价的取值范围.
【详解】(1)依题意可得:每件的销售利润为元,每月的销售量为件,
所以每月获得的利润与销售单价x的函数关系式为:
,
对称轴为,开口向下,此时最大值为,
所以利润与销售单价x的函数关系式,最大利润为元.
(2)由每月获得的利润不小于元,
得,
即 ,解得:,
这种节能灯的销售单价不得高于元,所以,
设政府每个月为他承担的总差价为元,
则,
由可得,
所以政府每个月为他承担的总差价的取值范围是元.
16..
【分析】根据题意,求得,根据二次函数的性质结合零点存在性定理,列出不等式,则问题得解.
【详解】因为,
①当时,根据零点存在性定理,显然在区间有根,
即,解得;
②当时,即时,此时,有,舍去;
③当时,即时,此时,有或,舍去,
④当时,即时,此时在上有两个实根,
显然不等式无解.
综上所述:.
【点睛】本题考查根据一元二次方程根的分布求参数范围,属中档题.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
