(2022新课标新教材)人教版六年级数学上册5.3圆的面积(3) 课件(共24张PPT)
文档属性
| 名称 | (2022新课标新教材)人教版六年级数学上册5.3圆的面积(3) 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 20.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 13:41:09 | ||
图片预览







文档简介
(共24张PPT)
2022秋 人教数学
六年级上册
5 圆
5.3 圆的面积(3)
使学生理解内接正方形和外切正方形的含义,掌握圆与内接正方形、外切正方形之间面积的计算方法。(重点)
2. 运用转化、添加辅助线等方法引导学生利用问题中的可用信息计算不规则图形的面积。(难点)
3. 在解决具体问题的基础上发现更为一般的数学规律,提高发现问题、提出问题、分析问题、解决问题的能力。
学习目标
情境导入
中国建筑中经常能见到“外方内圆”和“外圆内方”的设计。
情境导入
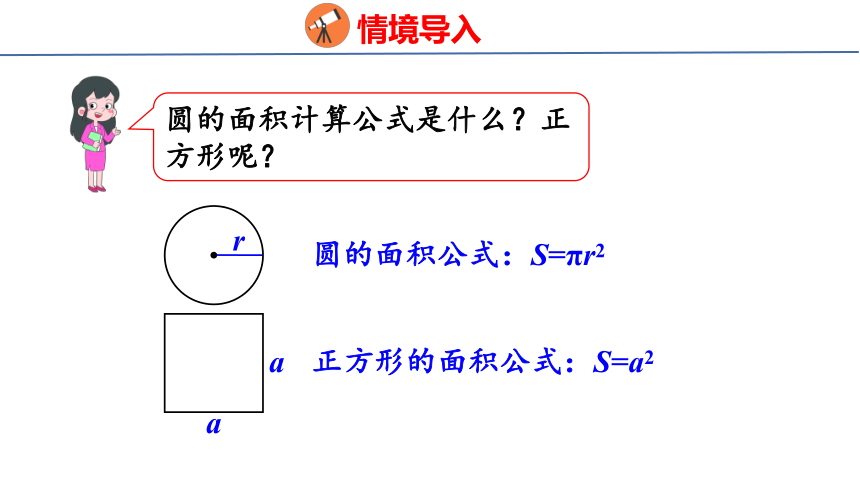
圆的面积计算公式是什么?正方形呢?
圆的面积公式:S=πr2
正方形的面积公式:S=a2
r
a
a
中国建筑中经常能见到“外方内圆”和“外圆内方”的设计。下图中的两个圆半径都是1 m,你能求出正方形和圆之间部分的面积吗?(教材P67例3)
探索新知
2
探索新知
阅读与理解
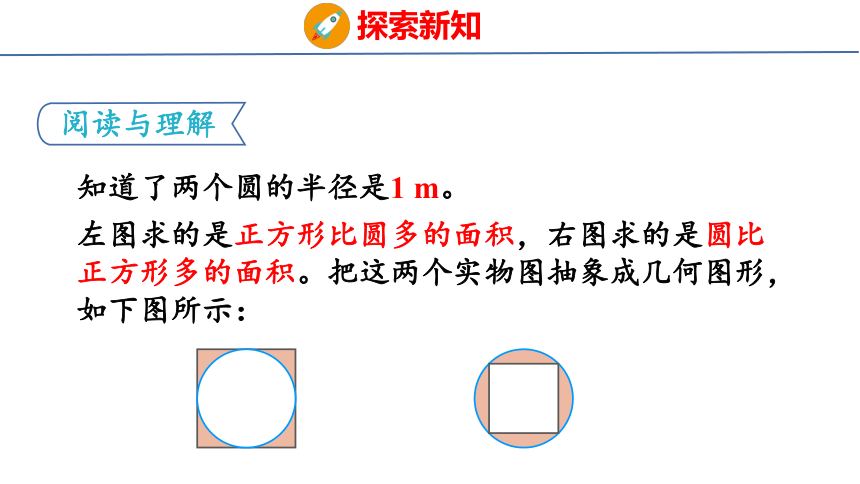
知道了两个圆的半径是1 m。
左图求的是正方形比圆多的面积,右图求的是圆比正方形多的面积。把这两个实物图抽象成几何图形,如下图所示:
探索新知
分析与解答
正方形的面积:2×2=4(m2)
正方形比圆多的面积:4-3.14=0.86(m2)
圆的面积:3.14×12=3.14(m )
从图(1)中可以看出:
“外方内圆”中正方形的边长与圆的直径长度相等。
图(1)
探索新知
可是“外圆内方”中正方形的边长是多少呢?
可以把“外圆内方”中的正方形看成两个三角形,它们的底等于圆的直径,高等于圆的半径。
圆比正方形多的面积:3.14-2=1.14(m2)
从图(2)中可以看出:
图(2)
正方形的面积: ×2=2(m2)
探索新知
回顾与反思
如果两个圆的半径都是r,结果又是怎样的?
答:左图中正方形与圆之间的面积是0.86 m2,右图中圆与正方形之间的面积是1.14 m2。
图(1):(2r)2-3.14×r2=0.86r2
当r=1 m时,和前面的结果完全一致。
图(2):3.14×r2- ×2=1.14r2
探索新知
1. 在正方形内画一个最大的圆,圆的直径=正方形的边长。如果圆的半径为r,那么正方形和圆之间部分的面积为0.86r2。
2. 在圆内画一个最大的正方形,正方形的对角线=圆的直径。如果圆的半径为r,那么圆和正方形之间部分的面积为1.14r2。
r
r
探索新知
马路上的大多数井盖都是圆形的,这是为什么呢?
井盖的平面轮廓呈圆形的一个原因是圆形井盖怎么放都不会掉到井里,并且能恰好盖住井口。这里利用了同一圆的直径都相等的性质。
生活中的数学
探索新知
生活中的数学
如果你仔细观察,就会发现,我们周围的很多东西的平面轮廓都是圆形的,如车轮是圆形的,这是为什么呢?
车轮的平面轮廓呈圆形是利用同一圆的半径都相等的性质,把车轴装在车轮的圆心上。车轮在地面上滚动的时候,车轴离地面的距离总是等于车轮的半径,因此只要道路平坦,车子就平稳地在地面上行驶。
随堂小练
1.下图是一面我国唐代铜镜的背面。铜镜的直径是24 cm。外面的圆与内部的正方形之间部分的面积是多少?(教材P66做一做)
做一做
3.14×(24÷2) =452.16(cm )
452.16-288=164.16(cm )
答:外面的圆与内部的正方形之间的面积是164.16 cm 。
×24 × 12 × 2=288(cm )
随堂小练
2.右图中铜钱的直径28 mm,中间正方形的边长为6 mm。这枚铜钱的面积是多少?(教材P70练习十五第9题)
3.14×(28÷2)2- 6 =579.44(mm )
答:这枚铜钱的面积是579.44 mm2。
随堂小练
3.如右图,一个运动场两端是半圆形,中间是长方形。这个运动场的周长是多少米?面积是多少平方米?(教材P70练习十五第10题)
2×3.14×32+100×2= 400.96(m)
答:这个运动场的周长是400.96 m,面积是9615.36 m2。
100 m
32 m
O
3.14×322+100×(32×2)= 9615.36(m2)
随堂小练
4.右图中的花瓣状门洞的边是由4个直径都是1 m的半圆组成的。这个门洞的周长和面积分别是多少?(教材P71练习十五第11题)
2×3.14×1= 6.28(m)
2×3.14×(1÷2)2 + 12= 2.57(m2)
答:这个门洞的周长是6.28 m,面积是2.57 m2。
1.求下面各图中涂色部分的面积。(单位:cm)
当堂检测
3.14×(16÷2)2÷2-16×(16÷2)÷2
=36.48(cm2)
12×6-3.14×62÷2
=15.48 (cm2)
2.下图中圆的周长是18.84 cm,圆的面积正好与长方形面积相等。求涂色部分的面积。
当堂检测
18.84÷3.14÷2=3(cm)
答:涂色部分的面积是21.195 cm2。
3.14×32× =21.195(cm2)
3.如图,公园有两块半圆形的草坪,它们的周长都是128.5 m,这两块草坪的总面积是多少?(教材P71练习十五第14题)
当堂检测
3.14×252 =196.25(m2)
答:这两块草坪的总面积是196.25 m2。
r=25
10÷2=5(dm)
(3.14×52÷2-10×5÷2)×2=25.8(dm2)
答:图中涂色部分的面积是25.8 dm2。
当堂检测
4.右图是由两个相同的半圆叠拼而成的。已知△ABC是一个等腰直角三角形,AB=BC=10 dm。图中涂色部分的面积是多少平方分米?(教材P72练习十五第16题)
学习完本节课,你有什么收获?
课堂小结
课堂小结
1. 在正方形内画一个最大的圆,圆的直径=正方形的边长。如果圆的半径为r,那么正方形和圆之间部分的面积为0.86r2。
2. 在圆内画一个最大的正方形,正方形的对角线=圆的直径。如果圆的半径为r,那么圆和正方形之间部分的面积为1.14r2。
r
r
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
2022秋 人教数学
六年级上册
5 圆
5.3 圆的面积(3)
使学生理解内接正方形和外切正方形的含义,掌握圆与内接正方形、外切正方形之间面积的计算方法。(重点)
2. 运用转化、添加辅助线等方法引导学生利用问题中的可用信息计算不规则图形的面积。(难点)
3. 在解决具体问题的基础上发现更为一般的数学规律,提高发现问题、提出问题、分析问题、解决问题的能力。
学习目标
情境导入
中国建筑中经常能见到“外方内圆”和“外圆内方”的设计。
情境导入
圆的面积计算公式是什么?正方形呢?
圆的面积公式:S=πr2
正方形的面积公式:S=a2
r
a
a
中国建筑中经常能见到“外方内圆”和“外圆内方”的设计。下图中的两个圆半径都是1 m,你能求出正方形和圆之间部分的面积吗?(教材P67例3)
探索新知
2
探索新知
阅读与理解
知道了两个圆的半径是1 m。
左图求的是正方形比圆多的面积,右图求的是圆比正方形多的面积。把这两个实物图抽象成几何图形,如下图所示:
探索新知
分析与解答
正方形的面积:2×2=4(m2)
正方形比圆多的面积:4-3.14=0.86(m2)
圆的面积:3.14×12=3.14(m )
从图(1)中可以看出:
“外方内圆”中正方形的边长与圆的直径长度相等。
图(1)
探索新知
可是“外圆内方”中正方形的边长是多少呢?
可以把“外圆内方”中的正方形看成两个三角形,它们的底等于圆的直径,高等于圆的半径。
圆比正方形多的面积:3.14-2=1.14(m2)
从图(2)中可以看出:
图(2)
正方形的面积: ×2=2(m2)
探索新知
回顾与反思
如果两个圆的半径都是r,结果又是怎样的?
答:左图中正方形与圆之间的面积是0.86 m2,右图中圆与正方形之间的面积是1.14 m2。
图(1):(2r)2-3.14×r2=0.86r2
当r=1 m时,和前面的结果完全一致。
图(2):3.14×r2- ×2=1.14r2
探索新知
1. 在正方形内画一个最大的圆,圆的直径=正方形的边长。如果圆的半径为r,那么正方形和圆之间部分的面积为0.86r2。
2. 在圆内画一个最大的正方形,正方形的对角线=圆的直径。如果圆的半径为r,那么圆和正方形之间部分的面积为1.14r2。
r
r
探索新知
马路上的大多数井盖都是圆形的,这是为什么呢?
井盖的平面轮廓呈圆形的一个原因是圆形井盖怎么放都不会掉到井里,并且能恰好盖住井口。这里利用了同一圆的直径都相等的性质。
生活中的数学
探索新知
生活中的数学
如果你仔细观察,就会发现,我们周围的很多东西的平面轮廓都是圆形的,如车轮是圆形的,这是为什么呢?
车轮的平面轮廓呈圆形是利用同一圆的半径都相等的性质,把车轴装在车轮的圆心上。车轮在地面上滚动的时候,车轴离地面的距离总是等于车轮的半径,因此只要道路平坦,车子就平稳地在地面上行驶。
随堂小练
1.下图是一面我国唐代铜镜的背面。铜镜的直径是24 cm。外面的圆与内部的正方形之间部分的面积是多少?(教材P66做一做)
做一做
3.14×(24÷2) =452.16(cm )
452.16-288=164.16(cm )
答:外面的圆与内部的正方形之间的面积是164.16 cm 。
×24 × 12 × 2=288(cm )
随堂小练
2.右图中铜钱的直径28 mm,中间正方形的边长为6 mm。这枚铜钱的面积是多少?(教材P70练习十五第9题)
3.14×(28÷2)2- 6 =579.44(mm )
答:这枚铜钱的面积是579.44 mm2。
随堂小练
3.如右图,一个运动场两端是半圆形,中间是长方形。这个运动场的周长是多少米?面积是多少平方米?(教材P70练习十五第10题)
2×3.14×32+100×2= 400.96(m)
答:这个运动场的周长是400.96 m,面积是9615.36 m2。
100 m
32 m
O
3.14×322+100×(32×2)= 9615.36(m2)
随堂小练
4.右图中的花瓣状门洞的边是由4个直径都是1 m的半圆组成的。这个门洞的周长和面积分别是多少?(教材P71练习十五第11题)
2×3.14×1= 6.28(m)
2×3.14×(1÷2)2 + 12= 2.57(m2)
答:这个门洞的周长是6.28 m,面积是2.57 m2。
1.求下面各图中涂色部分的面积。(单位:cm)
当堂检测
3.14×(16÷2)2÷2-16×(16÷2)÷2
=36.48(cm2)
12×6-3.14×62÷2
=15.48 (cm2)
2.下图中圆的周长是18.84 cm,圆的面积正好与长方形面积相等。求涂色部分的面积。
当堂检测
18.84÷3.14÷2=3(cm)
答:涂色部分的面积是21.195 cm2。
3.14×32× =21.195(cm2)
3.如图,公园有两块半圆形的草坪,它们的周长都是128.5 m,这两块草坪的总面积是多少?(教材P71练习十五第14题)
当堂检测
3.14×252 =196.25(m2)
答:这两块草坪的总面积是196.25 m2。
r=25
10÷2=5(dm)
(3.14×52÷2-10×5÷2)×2=25.8(dm2)
答:图中涂色部分的面积是25.8 dm2。
当堂检测
4.右图是由两个相同的半圆叠拼而成的。已知△ABC是一个等腰直角三角形,AB=BC=10 dm。图中涂色部分的面积是多少平方分米?(教材P72练习十五第16题)
学习完本节课,你有什么收获?
课堂小结
课堂小结
1. 在正方形内画一个最大的圆,圆的直径=正方形的边长。如果圆的半径为r,那么正方形和圆之间部分的面积为0.86r2。
2. 在圆内画一个最大的正方形,正方形的对角线=圆的直径。如果圆的半径为r,那么圆和正方形之间部分的面积为1.14r2。
r
r
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
