(2022新课标新教材)人教版 六年级上册6.5求比一个数多(少)百分之多少的数是多少 课件(共28张PPT)
文档属性
| 名称 | (2022新课标新教材)人教版 六年级上册6.5求比一个数多(少)百分之多少的数是多少 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 16:14:33 | ||
图片预览








文档简介
(共28张PPT)
2022秋 人教数学
六年级上册
6 百分数(一)
6.5 求比一个数多(少)百分之多少的数是多少
掌握“求比一个数多(少)百分之多少的数是多少”的解题方法。(重点)
2. 正确、灵活地解答“求比一个数多(少)百分之多少的数是多少”的实际问题。
学习目标
回顾复习
学校图书室原有图书1400册,今年图书册数增加了 。现在图书室有多少册图书?
3
25
找出上面问题的单位“1”,并根据数量关系列式:
单位“1”
方法一:先求增加了多少本,
再与原来本数相加。
1400+1400×
3
25
方法二:先求现在本数是原
来的几分之几,再
与原来本数相乘。
1400× 1+
3
25
想一想,说一说:如何求比一个数多(少)几分之几的数是多少。
先找到单位“1”
可以先求比单位“1”多(少)多少
若将题目中的分数换成百分数,应怎样解决这个问题呢?这节课我们来学习,“求一个数比另一个数多(少)百分之多少”的问题。
回顾复习
也可以先求这个数是单位“1”的几分之几
学校图书室原有图书1400册,今年图书数量增加了12%。现在图书室有多少册图书?(教材P88例4)
探索新知
4
已知信息 所求问题
①学校图书室原有图书1400册; ②今年图书数量增加了12% 现在图书室有多少册图书
探索新知
今年图书数量比原有图书数量增加了12%,是把原有图书数量(1400册)看作单位“1”。
已知信息 所求问题
①学校图书室原有图书1400册; ②今年图书数量增加了12% 现在图书室有多少册图书
探索新知
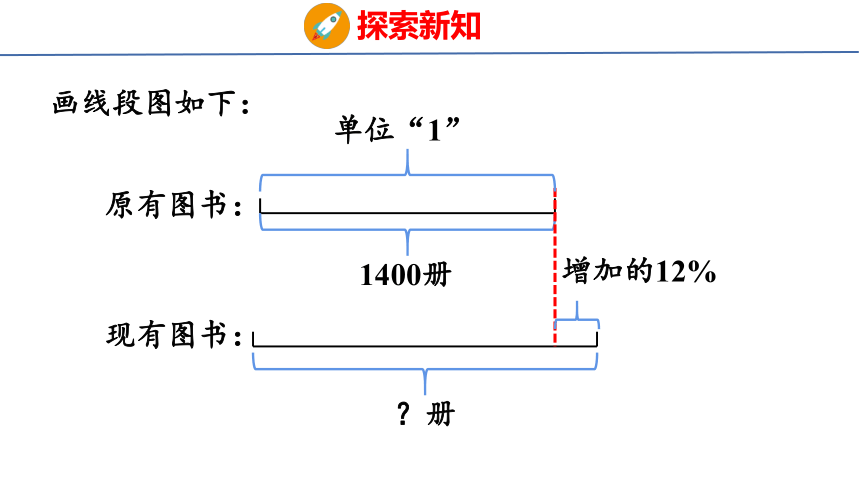
画线段图如下:
原有图书:
现有图书:
1400册
?册
增加的12%
单位“1”
探索新知
解题方法:
方法一:先求今年增加的图书数量,再求现在有多少册图书。
增加的图书数量=原有的图书数量×12%
现有的图书数量=原有的图书数量 +增加的图书数量
探索新知
解题方法:
方法二:先求今年图书数量是去年的百分之多少,再求现在有多少册图书。
今年图书数量是去年的(1+12%)
现有的图书数量=原有的图书数量 ×(1+12%)
探索新知
方法一:
1400×12%=168(册)
方法二:
1400×(1+12%)=1568(册)
答:现在图书室有1568册图书。
1400 + 168=1568(册)
增加的12%
相当于原来的百分之多少
“求比一个数多(少)百分之多少的数是多少”的问题的方法。
探索新知
方法一:单位“1”的量±单位“1”的量×比单位“1”的量多(少)的百分之多少=这个数量;
方法二:单位“1”的量×[1±比单位“1”的量多(少)的百分之多少]=这个数量。
随堂小练
1.龙泉镇去年有小学生2800人,今年比去年减少了0.5%。今年有小学生多少人?(教材P89做一做)
做一做
单位“1”
方法一:
2800-2800×0.5%=2786(人)
方法二:
2800×(1-0.5%)=2786(人)
答:今年有小学生2786人。
随堂小练
2.填空。
(1)50 m的30%是( )m,比50 m多20%是( )m,比50 m少20%的是( )m。
(2)光明小学的男生人数比女生人数多3%,是把( )看作单位“1”,男生人数相当于女生的( )%。
15
60
40
女生人数
103
随堂小练
3.养鸡场用2400个鸡蛋孵小鸡,有5%没有孵出来。孵出来的小鸡有多少只?(教材P91练习十九第7题)
2400-2400×5%=2280(只)
答:孵出来的小鸡有2280只。
方法一:
先求没有孵出来的小鸡的数量。
随堂小练
3.养鸡场用2400个鸡蛋孵小鸡,有5%没有孵出来。孵出来的小鸡有多少只?(教材P91练习十九第7题)
2400×(1-5%)=2280(只)
答:孵出来的小鸡有2280只。
方法二:
先求孵出来的小鸡占总数量的百分之多少。
随堂小练
4.企鹅共有18个独立物种,其中体型最小的物种是小蓝企鹅,约0.4 m高;体型最大的物种是帝企鹅,比小蓝企鹅约高175%,帝企鹅约高多少米?
0.4×(1+175%)=1.1(m)
答:帝企鹅约高1.1 m。
1.曙光小学以往的跳高记录是1.3 m,本次比赛中王平的跳高成绩比这一记录高了10%。王平的跳高成绩是多少?(教材P91练习十九第8题)
当堂检测
1.3×(1+10%)=1.43(m)
答:王平的跳高成绩是1.43 m。
2.早茶是传统的中国社交饮食习俗,也是广东传统文化中浓墨重彩的一笔。今天淘淘吃早茶花费了18元,悄悄多点了一份叉烧包,比淘淘多花了30%,今天两人吃早茶共花费了多少元?
当堂检测
18×(1+30%)=23.4(元)
18+23.4=41.4(元)
答:今天两人吃早茶共花费了41.4元。
3.学校社团活动课,有40人参加书法小组,参加科技创新小组的人数比参加书法小组的多40%。有多少人参加科技创新小组。
当堂检测
40×(1+40%)=56(人)
答:有56人参加科技创新小组。
4.袁隆平院士是我国著名科学家,被誉为“杂交水稻之父”。2021年,袁隆平院士指导的杂交水稻示范片双季水稻年平均产量达到了每公顷24.06 t,比攻关目标高了约7%。攻关目标约是每公顷多少吨?(得数保留一位小数。)(教材P91练习十九第10题)
当堂检测
单位“1”,且单位“1”的量未知
当堂检测
画线段图如下:
攻关目标:
双季稻:
? t
24.06 t
比攻关目标,高了约7%
单位“1”
当堂检测
数量关系为:
比单位“1”的量多的产量
=
单位“1”的量
×
7%
单位“1”的量
+
单位“1”的量
×
7%
=
双季稻年平均每公顷产量(24.06 t)
可设单位“1”的量为x,根据数量关系列方程解答;也可以用算数法解答。
当堂检测
方法一:
设攻关目标约是每公顷x t。
x+7%x=24.06
x≈22.5
方法二:
24.06÷(1+7%)=22.5(t)
答:攻关目标约是每公顷22.5 t。
学习完本节课,你有什么收获?
课堂小结
课堂小结
方法一:单位“1”的量±单位“1”的量×比单位“1”的量多(少)的百分之多少=这个数量;
方法二:单位“1”的量×[1±比单位“1”的量多(少)的百分之多少]=这个数量。
“求比一个数多(少)百分之多少的数是多少”的问题的方法。
课堂小结
方法一:单位“1”的量±单位“1”的量×比单位“1”的量多(少)百分之多少=已知量,据此列方程解答。
方法二:已知量÷[1±比单位“1”的量多(少)百分之多少,据此列方程解答。
“已知比一个数多(少)百分之几的数是多少,求这个数”问题的解题方法:
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
2022秋 人教数学
六年级上册
6 百分数(一)
6.5 求比一个数多(少)百分之多少的数是多少
掌握“求比一个数多(少)百分之多少的数是多少”的解题方法。(重点)
2. 正确、灵活地解答“求比一个数多(少)百分之多少的数是多少”的实际问题。
学习目标
回顾复习
学校图书室原有图书1400册,今年图书册数增加了 。现在图书室有多少册图书?
3
25
找出上面问题的单位“1”,并根据数量关系列式:
单位“1”
方法一:先求增加了多少本,
再与原来本数相加。
1400+1400×
3
25
方法二:先求现在本数是原
来的几分之几,再
与原来本数相乘。
1400× 1+
3
25
想一想,说一说:如何求比一个数多(少)几分之几的数是多少。
先找到单位“1”
可以先求比单位“1”多(少)多少
若将题目中的分数换成百分数,应怎样解决这个问题呢?这节课我们来学习,“求一个数比另一个数多(少)百分之多少”的问题。
回顾复习
也可以先求这个数是单位“1”的几分之几
学校图书室原有图书1400册,今年图书数量增加了12%。现在图书室有多少册图书?(教材P88例4)
探索新知
4
已知信息 所求问题
①学校图书室原有图书1400册; ②今年图书数量增加了12% 现在图书室有多少册图书
探索新知
今年图书数量比原有图书数量增加了12%,是把原有图书数量(1400册)看作单位“1”。
已知信息 所求问题
①学校图书室原有图书1400册; ②今年图书数量增加了12% 现在图书室有多少册图书
探索新知
画线段图如下:
原有图书:
现有图书:
1400册
?册
增加的12%
单位“1”
探索新知
解题方法:
方法一:先求今年增加的图书数量,再求现在有多少册图书。
增加的图书数量=原有的图书数量×12%
现有的图书数量=原有的图书数量 +增加的图书数量
探索新知
解题方法:
方法二:先求今年图书数量是去年的百分之多少,再求现在有多少册图书。
今年图书数量是去年的(1+12%)
现有的图书数量=原有的图书数量 ×(1+12%)
探索新知
方法一:
1400×12%=168(册)
方法二:
1400×(1+12%)=1568(册)
答:现在图书室有1568册图书。
1400 + 168=1568(册)
增加的12%
相当于原来的百分之多少
“求比一个数多(少)百分之多少的数是多少”的问题的方法。
探索新知
方法一:单位“1”的量±单位“1”的量×比单位“1”的量多(少)的百分之多少=这个数量;
方法二:单位“1”的量×[1±比单位“1”的量多(少)的百分之多少]=这个数量。
随堂小练
1.龙泉镇去年有小学生2800人,今年比去年减少了0.5%。今年有小学生多少人?(教材P89做一做)
做一做
单位“1”
方法一:
2800-2800×0.5%=2786(人)
方法二:
2800×(1-0.5%)=2786(人)
答:今年有小学生2786人。
随堂小练
2.填空。
(1)50 m的30%是( )m,比50 m多20%是( )m,比50 m少20%的是( )m。
(2)光明小学的男生人数比女生人数多3%,是把( )看作单位“1”,男生人数相当于女生的( )%。
15
60
40
女生人数
103
随堂小练
3.养鸡场用2400个鸡蛋孵小鸡,有5%没有孵出来。孵出来的小鸡有多少只?(教材P91练习十九第7题)
2400-2400×5%=2280(只)
答:孵出来的小鸡有2280只。
方法一:
先求没有孵出来的小鸡的数量。
随堂小练
3.养鸡场用2400个鸡蛋孵小鸡,有5%没有孵出来。孵出来的小鸡有多少只?(教材P91练习十九第7题)
2400×(1-5%)=2280(只)
答:孵出来的小鸡有2280只。
方法二:
先求孵出来的小鸡占总数量的百分之多少。
随堂小练
4.企鹅共有18个独立物种,其中体型最小的物种是小蓝企鹅,约0.4 m高;体型最大的物种是帝企鹅,比小蓝企鹅约高175%,帝企鹅约高多少米?
0.4×(1+175%)=1.1(m)
答:帝企鹅约高1.1 m。
1.曙光小学以往的跳高记录是1.3 m,本次比赛中王平的跳高成绩比这一记录高了10%。王平的跳高成绩是多少?(教材P91练习十九第8题)
当堂检测
1.3×(1+10%)=1.43(m)
答:王平的跳高成绩是1.43 m。
2.早茶是传统的中国社交饮食习俗,也是广东传统文化中浓墨重彩的一笔。今天淘淘吃早茶花费了18元,悄悄多点了一份叉烧包,比淘淘多花了30%,今天两人吃早茶共花费了多少元?
当堂检测
18×(1+30%)=23.4(元)
18+23.4=41.4(元)
答:今天两人吃早茶共花费了41.4元。
3.学校社团活动课,有40人参加书法小组,参加科技创新小组的人数比参加书法小组的多40%。有多少人参加科技创新小组。
当堂检测
40×(1+40%)=56(人)
答:有56人参加科技创新小组。
4.袁隆平院士是我国著名科学家,被誉为“杂交水稻之父”。2021年,袁隆平院士指导的杂交水稻示范片双季水稻年平均产量达到了每公顷24.06 t,比攻关目标高了约7%。攻关目标约是每公顷多少吨?(得数保留一位小数。)(教材P91练习十九第10题)
当堂检测
单位“1”,且单位“1”的量未知
当堂检测
画线段图如下:
攻关目标:
双季稻:
? t
24.06 t
比攻关目标,高了约7%
单位“1”
当堂检测
数量关系为:
比单位“1”的量多的产量
=
单位“1”的量
×
7%
单位“1”的量
+
单位“1”的量
×
7%
=
双季稻年平均每公顷产量(24.06 t)
可设单位“1”的量为x,根据数量关系列方程解答;也可以用算数法解答。
当堂检测
方法一:
设攻关目标约是每公顷x t。
x+7%x=24.06
x≈22.5
方法二:
24.06÷(1+7%)=22.5(t)
答:攻关目标约是每公顷22.5 t。
学习完本节课,你有什么收获?
课堂小结
课堂小结
方法一:单位“1”的量±单位“1”的量×比单位“1”的量多(少)的百分之多少=这个数量;
方法二:单位“1”的量×[1±比单位“1”的量多(少)的百分之多少]=这个数量。
“求比一个数多(少)百分之多少的数是多少”的问题的方法。
课堂小结
方法一:单位“1”的量±单位“1”的量×比单位“1”的量多(少)百分之多少=已知量,据此列方程解答。
方法二:已知量÷[1±比单位“1”的量多(少)百分之多少,据此列方程解答。
“已知比一个数多(少)百分之几的数是多少,求这个数”问题的解题方法:
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
