(2022新课标新教材)6.6用百分数知识解决问题 课件(共24张PPT)
文档属性
| 名称 | (2022新课标新教材)6.6用百分数知识解决问题 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 12.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 16:17:45 | ||
图片预览








文档简介
(共24张PPT)
2022秋 人教数学
六年级上册
6 百分数(一)
6.6 用百分数的知识解决问题
学生能够尝试用假设法解决连续求“一个数比另一个数多(或少)百分之几”的问题。(重点)
2. 掌握用抽象“1”解决实际问题的方法。(难点)
学习目标
回顾复习
元旦期间某书店所有的书均降价20%销售。
(1)阳阳购买了原价25元的一本书,现在只需要支付多少钱?
25×(1-20%)=20(元)
答:现在只需要支付20元钱。
(2)若阳阳刚办了这家店的会员,可以在降价基础上再降价10%,那么现在只需要支付多少钱?
20×(1-10%)=18(元)
答:现在只需要支付18元钱。
在刚才的计算过程中,单位“1”分别是谁?
第一问中单位“1”是原价(25元)
回顾复习
用会员的价钱与原价相比降了多少呢?今天我们来学习一个量的连续变化相关知识。
第二问中单位“1”是降价20%后的价钱(20元)
某种商品4月份的价格比3月份降了20%,5月份的价格比4月份又涨了20%。5月份的价格和3月份相比是涨了还是降了?变化幅度是多少?(教材P88例5)
探索新知
5
找单位“1”
单位“1”
单位“1”
探索新知
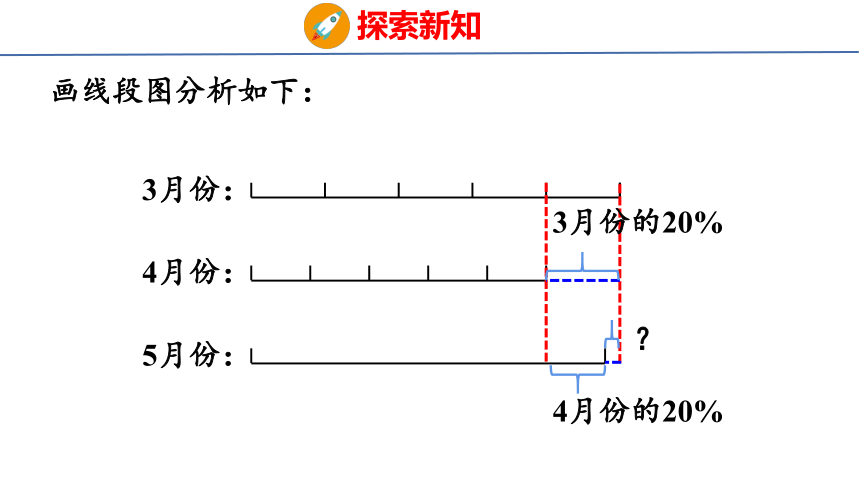
画线段图分析如下:
3月份:
4月份:
5月份:
3月份的20%
4月份的20%
?
探索新知
3月份的价格×(1-20%)=4月份的价格
4月份的价格×(1+20%)=5月份的价格
变化幅度=5月份的价格与3月份的价格差÷三月份的价格。
可是不知道商品原来的价格啊。
探索新知
解题方法:
方法一:可以假设此商品3月份的价格是100元。
4月份价格:100×(1-20%)=80(元)
5月份价格:80×(1+20%)=96(元)
5月份与3月份比较:96<100,降了。
变化幅度:(100-96)÷100=4%
答:5月份的价格和3月份相比降了,变化幅度是降了4%。
探索新知
解题方法:
方法二:也可以直接假设此商品3月份的价格是“1”。
4月份价格:1×(1-20%)=0.8
5月份价格:0.8×(1+20%)=0.96
5月份与3月份比较:0.96<1,降了。
变化幅度:(1-0.96)÷1=4%
答:5月份的价格和3月份相比降了,变化幅度是降了4%。
探索新知
回顾与反思
如果此商品3月份的价格是a元,结论是否一致?
a×(1-20%)×(1+20%)=0.96a
(a-0.96a)÷a=4%
结论一致
探索新知
回顾与反思
虽然降价和涨价幅度都是20%,但降价和涨价的具体钱数却不同。
因为单位“1”不同,所以价格发生了变化。解题关键是弄清两次变价的标准量。
解决变化幅度问题的关键是找准单位“1”,可以假设单位“1”的量是一个具体的数,也可以假设单位“1”的量是1。求出最后的比较量,再求变化幅度。
变化幅度问题的解决方法
探索新知
随堂小练
1.某电视机厂计划某种型号的电视机比去年增产50%,实际又比计划产量多生产了10%。此型号的电视机今年的实际产量是去年的百分之多少?(教材P89做一做第3题)
做一做
单位“1”
单位“1”
1×(1+50%)×(1+10%)÷1=165%
答:此型号的电视机今年的实际产量是去年的165%。
假设去年产量是1。
随堂小练
2. 8月初鸡蛋价格比7月初上涨了10%,9月初又比8月初回落了15%。9月初鸡蛋价格与7月初相比是涨了还是跌了?涨跌幅度是多少?(教材P91练习十九第11题)
1×(1+10%)×(1-15%)=0.935
答:9月初鸡蛋价格与7月初相比是跌了,跌幅是6.5%。
假设7月初鸡蛋价格是1。
(1-0.935)÷1=6.5%
0.935<1
随堂小练
3.某种蔬菜3月第二周比第一周降价5%,第三周比第二周又降价5%。两周以来共降价百分之多少?(教材P91练习十九第12题)
1×(1-5%)×(1-5%)=0.9025
答:两周以来共降价9.75%。
(1-0.9025)÷1=9.75%
随堂小练
4.万佳超市出售一种篮球,一星期后,超市把售价降低了15%,再过一星期右提升了30%。这时篮球的价格比最初相比是涨了还是降了?涨或降的幅度是多少?
1×(1-15%)×(1+30%)=1.105
答:这时篮球的价格比最初相比是涨了,涨幅是10.5%。
(1.105-1)÷1=10.5%
1.105>1
1.某品牌的手机进行促销活动,降价8%。在此基础上,商场又返还实际售价5%的现金。此时买这个品牌的手机,相当于降价百分之多少?(教材P91练习十九第13题)
当堂检测
1×(1-8%)×(1-5%)=0.874
答:相当于降价12.6%。
(1-0.874)÷1=12.6%
2. 五月初,某批发市场牛肉的价格比四月初回落了10%,六月初又比五月初上涨了8%。六月初牛肉的价格比四月初是涨了还是降了?涨或降的幅度是多少?
当堂检测
1×(1-10%)×(1+8%)=0.972
答:六月初牛肉的价格比四月初是降了,降幅是2.8%。
(1-0.972)÷1=2.8%
0.972<1
3.(易错题)判断:一种商品,先提价10%,再降价10%,则此商品的现价与原价相同。 ( )
错解: √
正解:×
反思:错解忽略了两个10%对应的单位“1”的量不同。
解决此类问题时,要弄清楚两次变化幅度的单位“1”的量分别是多少。
当堂检测
4.运动鞋专卖店针对原价1200元的新款运动鞋在店庆期间降价20%出售,现活动结束调回原价,需要提价百分之多少?
当堂检测
1200×(1-20%)=960(元)
答:需要提价25%。
(1200-960)÷960=25%
学习完本节课,你有什么收获?
课堂小结
课堂小结
解决变化幅度问题的关键是找准单位“1”,可以假设单位“1”的量是一个具体的数,也可以假设单位“1”的量是1。求出最后的比较量,再求变化幅度。
变化幅度问题的解决方法
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
2022秋 人教数学
六年级上册
6 百分数(一)
6.6 用百分数的知识解决问题
学生能够尝试用假设法解决连续求“一个数比另一个数多(或少)百分之几”的问题。(重点)
2. 掌握用抽象“1”解决实际问题的方法。(难点)
学习目标
回顾复习
元旦期间某书店所有的书均降价20%销售。
(1)阳阳购买了原价25元的一本书,现在只需要支付多少钱?
25×(1-20%)=20(元)
答:现在只需要支付20元钱。
(2)若阳阳刚办了这家店的会员,可以在降价基础上再降价10%,那么现在只需要支付多少钱?
20×(1-10%)=18(元)
答:现在只需要支付18元钱。
在刚才的计算过程中,单位“1”分别是谁?
第一问中单位“1”是原价(25元)
回顾复习
用会员的价钱与原价相比降了多少呢?今天我们来学习一个量的连续变化相关知识。
第二问中单位“1”是降价20%后的价钱(20元)
某种商品4月份的价格比3月份降了20%,5月份的价格比4月份又涨了20%。5月份的价格和3月份相比是涨了还是降了?变化幅度是多少?(教材P88例5)
探索新知
5
找单位“1”
单位“1”
单位“1”
探索新知
画线段图分析如下:
3月份:
4月份:
5月份:
3月份的20%
4月份的20%
?
探索新知
3月份的价格×(1-20%)=4月份的价格
4月份的价格×(1+20%)=5月份的价格
变化幅度=5月份的价格与3月份的价格差÷三月份的价格。
可是不知道商品原来的价格啊。
探索新知
解题方法:
方法一:可以假设此商品3月份的价格是100元。
4月份价格:100×(1-20%)=80(元)
5月份价格:80×(1+20%)=96(元)
5月份与3月份比较:96<100,降了。
变化幅度:(100-96)÷100=4%
答:5月份的价格和3月份相比降了,变化幅度是降了4%。
探索新知
解题方法:
方法二:也可以直接假设此商品3月份的价格是“1”。
4月份价格:1×(1-20%)=0.8
5月份价格:0.8×(1+20%)=0.96
5月份与3月份比较:0.96<1,降了。
变化幅度:(1-0.96)÷1=4%
答:5月份的价格和3月份相比降了,变化幅度是降了4%。
探索新知
回顾与反思
如果此商品3月份的价格是a元,结论是否一致?
a×(1-20%)×(1+20%)=0.96a
(a-0.96a)÷a=4%
结论一致
探索新知
回顾与反思
虽然降价和涨价幅度都是20%,但降价和涨价的具体钱数却不同。
因为单位“1”不同,所以价格发生了变化。解题关键是弄清两次变价的标准量。
解决变化幅度问题的关键是找准单位“1”,可以假设单位“1”的量是一个具体的数,也可以假设单位“1”的量是1。求出最后的比较量,再求变化幅度。
变化幅度问题的解决方法
探索新知
随堂小练
1.某电视机厂计划某种型号的电视机比去年增产50%,实际又比计划产量多生产了10%。此型号的电视机今年的实际产量是去年的百分之多少?(教材P89做一做第3题)
做一做
单位“1”
单位“1”
1×(1+50%)×(1+10%)÷1=165%
答:此型号的电视机今年的实际产量是去年的165%。
假设去年产量是1。
随堂小练
2. 8月初鸡蛋价格比7月初上涨了10%,9月初又比8月初回落了15%。9月初鸡蛋价格与7月初相比是涨了还是跌了?涨跌幅度是多少?(教材P91练习十九第11题)
1×(1+10%)×(1-15%)=0.935
答:9月初鸡蛋价格与7月初相比是跌了,跌幅是6.5%。
假设7月初鸡蛋价格是1。
(1-0.935)÷1=6.5%
0.935<1
随堂小练
3.某种蔬菜3月第二周比第一周降价5%,第三周比第二周又降价5%。两周以来共降价百分之多少?(教材P91练习十九第12题)
1×(1-5%)×(1-5%)=0.9025
答:两周以来共降价9.75%。
(1-0.9025)÷1=9.75%
随堂小练
4.万佳超市出售一种篮球,一星期后,超市把售价降低了15%,再过一星期右提升了30%。这时篮球的价格比最初相比是涨了还是降了?涨或降的幅度是多少?
1×(1-15%)×(1+30%)=1.105
答:这时篮球的价格比最初相比是涨了,涨幅是10.5%。
(1.105-1)÷1=10.5%
1.105>1
1.某品牌的手机进行促销活动,降价8%。在此基础上,商场又返还实际售价5%的现金。此时买这个品牌的手机,相当于降价百分之多少?(教材P91练习十九第13题)
当堂检测
1×(1-8%)×(1-5%)=0.874
答:相当于降价12.6%。
(1-0.874)÷1=12.6%
2. 五月初,某批发市场牛肉的价格比四月初回落了10%,六月初又比五月初上涨了8%。六月初牛肉的价格比四月初是涨了还是降了?涨或降的幅度是多少?
当堂检测
1×(1-10%)×(1+8%)=0.972
答:六月初牛肉的价格比四月初是降了,降幅是2.8%。
(1-0.972)÷1=2.8%
0.972<1
3.(易错题)判断:一种商品,先提价10%,再降价10%,则此商品的现价与原价相同。 ( )
错解: √
正解:×
反思:错解忽略了两个10%对应的单位“1”的量不同。
解决此类问题时,要弄清楚两次变化幅度的单位“1”的量分别是多少。
当堂检测
4.运动鞋专卖店针对原价1200元的新款运动鞋在店庆期间降价20%出售,现活动结束调回原价,需要提价百分之多少?
当堂检测
1200×(1-20%)=960(元)
答:需要提价25%。
(1200-960)÷960=25%
学习完本节课,你有什么收获?
课堂小结
课堂小结
解决变化幅度问题的关键是找准单位“1”,可以假设单位“1”的量是一个具体的数,也可以假设单位“1”的量是1。求出最后的比较量,再求变化幅度。
变化幅度问题的解决方法
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
