(2022新课标新教材)人教版六年级上册8 数学广角——数与形 课件(共33张PPT)
文档属性
| 名称 | (2022新课标新教材)人教版六年级上册8 数学广角——数与形 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 12.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-24 14:34:41 | ||
图片预览








文档简介
(共33张PPT)
2022秋 人教数学
六年级上册
8 数学广角——数与形
通过自主探究发现图形中隐藏着的数的规律,并会应用所发现的规律。 (重点)
2. 会利用图形来解决一些有关数的问题。(重点)
3. 在解决问题的过程中,体会和掌握数形结合、归纳推理、极限等基本的数学思想。(难点)
学习目标
回顾复习
1+3=( )
1+3+5=( )
1+3+5+7=( )
1+3+5+7+9+…+21=( )(用计算器算一算)
计算出结果。
4
9
16
121
想一想,说一说:在刚才的计算中,你发现了什么?
算式左边是连续的奇数相加。
你能发现其中的规律吗?这节课我们学习数形结合的方法,使你能更快地发现规律,更容易地进行计算。
回顾复习
算式右边分别是2、3、4……的平方
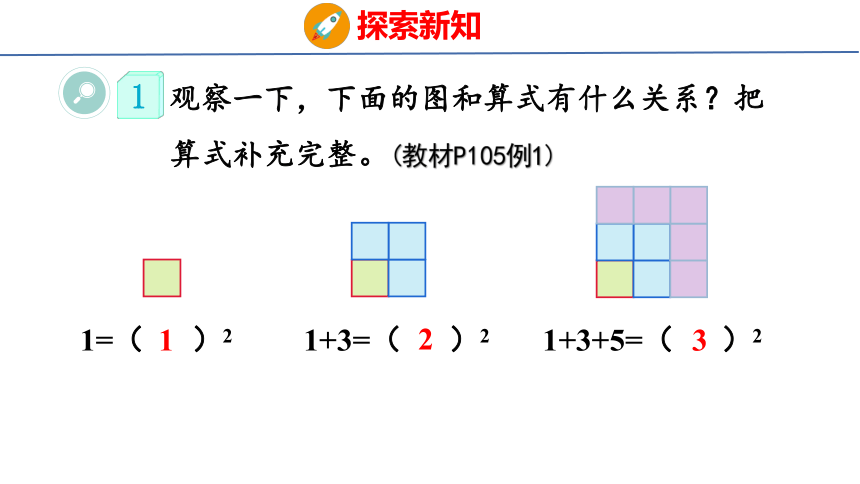
观察一下,下面的图和算式有什么关系?把算式补充完整。(教材P105例1)
探索新知
1
1=( )2
1+3=( )2
1+3+5=( )2
1
2
3
探索新知
图示 数形结合 看作大正方形
构图过程 小正方形个数
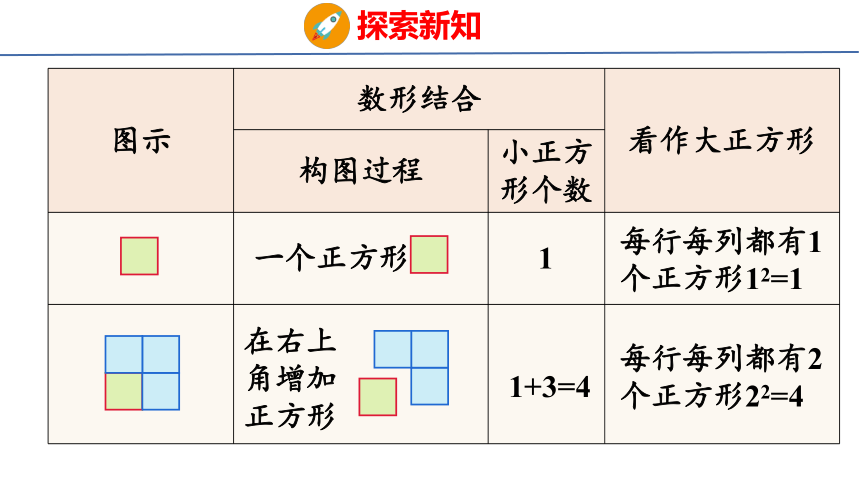
一个正方形
1
每行每列都有1个正方形12=1
在右上角增加正方形
1+3=4
每行每列都有2个正方形22=4
探索新知
图示 数形结合 看作大正方形
构图过程 小正方形个数
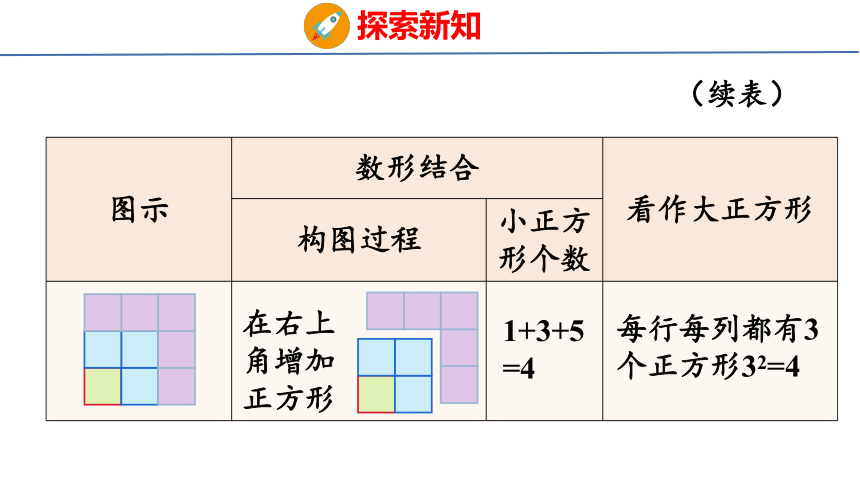
(续表)
在右上角增加正方形
1+3+5
=4
每行每列都有3个正方形32=4
探索新知
发现规律:
算式左边的加数是每个正方形图左下角的小正方形和其他“ ”形图中所包含的小正方形个数之和,正好等于每个正方形图中每列小正方形个数的平方。
探索新知
你能利用规律直接写一写吗?如果有困难,可以画图来帮助。
1+3+5+7=( )2
1+3+5+7+9+11+13=( )2
=92
4
7
1+3+5+7+9+11+13+15+17
探索新知
从1开始,连续几个奇数的和,即是几的平方。
运用数形结合发现规律,即借助图形分析并观察数在运算中的规律,以形助数。
探索新知
2
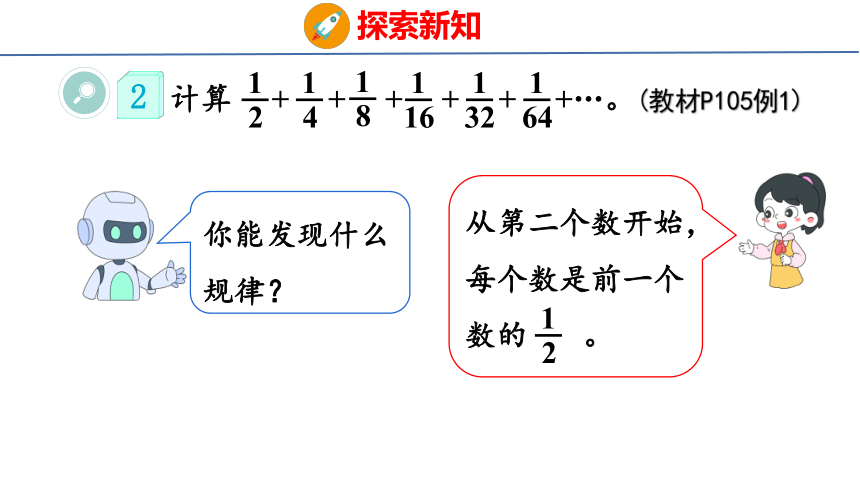
计算 + + + + + +…。(教材P105例1)
1
2
1
4
1
8
1
16
1
32
1
64
你能发现什么规律?
从第二个数开始,每个数是前一个数的 。
1
2
探索新知
按顺序计算:
+ =
1
2
1
4
3
4
+ + =
1
2
1
4
7
8
1
8
+ + + =
1
2
1
4
15
16
1
8
1
16
我一个一个加下去看看,答案好像有点规律。加下去,等号右边的分数越来越接近于1。
探索新知
画图分析、数形结合
用一个圆或一条线段表示“1”。
1
4
1
2
1
8
1
16
1
32
…
探索新知
1
2
1
4
1
8
1
16
1
32
…
+ + + + + +…=
1
2
1
4
1
8
1
16
1
32
1
64
1
从两幅图中可以看出:这些分数不断加下去,总和就是1。
有些问题通过画图解决起来更直观。
探索新知
数形结合是学习数学的一种重要的思想方法。运用数形结合的方法,可以帮助理解计算方法,进行计算。同时也可以探索数学规律,借此解决问题。
随堂小练
1.请你根据例1的结论算一算。(教材P106做一做第1题)
做一做
1+3+5+7+5+3+1=( )
1+3+5+7+9+11+13+11+9+7+5+3+1=( )
42
32
42+32
=25
72
62
85
随堂小练
2.下面每个图中各有多少个绿色小正方形和多少个蓝色小正方形?。(教材P106做一做第2题)
做一做
绿色:
1
2
3
4
蓝色:
8
10
12
14
随堂小练
从图中可以看出,第n个图形一共有3×(n+2)=3n+6个小正方形,其中有n块是绿色,3n+6-n=2n+6(块)是蓝色。
照这样接着画下去,第6个图形有多少个绿色小正方形和多少个蓝色小正方形?第10个图形呢?你能解释这其中的道理吗?
随堂小练
所以,第6个图形有6个绿色小正方形和18个蓝色小正方形;第10个图形有10个绿色小正方形和26个蓝色小正方形。
照这样接着画下去,第6个图形有多少个绿色小正方形和多少个蓝色小正方形?第10个图形呢?你能解释这其中的道理吗?
随堂小练
3.计算。
1- - - - =
1
2
1
4
1
8
1
16
1
16
1- - - - - … =
1
2
1
4
1
8
1
16
0
随堂小练
4.阳阳从家出发,骑车0.5时到达离家4 km的书店,在书店买书0.5时后步行回家,在步行2 km后遇到同学,与同学聊天0.5时,然后回家。图( )描述了阳阳的活动行程。
A
1.下面每个图中最外圈各有多少个小正方形?(教材P107练习二十二第1题)
当堂检测
32-1=8
52-32=16
72-52=24
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?你能解释其中的道理吗?
当堂检测
从图中可以看出,第n个图形的边长为2n+1,次外圈的边长(也就是上一个图形的边长)为2n-1,则第n个图形最外圈有(2n+1)2-(2n-1)2个小正方形。
当堂检测
所以第5个图形最外圈有:
(2×5+1)2-(2×5-1)2=112-92=40(个)小正方形。
2.(教材P107 练习二十二第2题)
当堂检测
1
3
6
10
请你根据上面图形与数的规律接着画一画,填一填。
15
21
28
2.(教材P107 练习二十二第2题)
当堂检测
1
3
6
10
如果不画,这样排列下去,第10个数是多少?
1+2+3+4+5+6+7+8+9+10=55
3.小林、小强、小丽、小兵和小刚5人进行象棋比赛,每两人之间都要下一盘。小林已经下了4盘,小强下了3盘,小丽下了2盘,小兵下了1盘。小刚一共下了几盘?分别和谁下的?(教材P109 练习二十二第6题)
当堂检测
用连线的方法试试。
3.小林、小强、小丽、小兵和小刚5人进行象棋比赛,每两人之间都要下一盘。小林已经下了4盘,小强下了3盘,小丽下了2盘,小兵下了1盘。小刚一共下了几盘?分别和谁下的?(教材P109 练习二十二第6题)
当堂检测
所以小刚一共下了2盘,分别是和小林、小强下的。
当堂检测
4.我国宋代数学家杨辉在1261年撰写了《详解九章算法》,他在这本著作中画了一个由数构成的三角形图,我们把它称为“杨辉三角”。你能发现右面“杨辉三角”图中各数之间的关系吗 你能按照发现的规律把这个三角形图继续写下去吗 试试看。(教材P109 练习二十二第7题)
每个数字是上一行的左右两个数字之和。继续写下去,下一行是:1 6 15 20 15 6 1 。
学习完本节课,你有什么收获?
课堂小结
课堂小结
从1开始,连续几个奇数的和,即是几的平方。
数形结合是学习数学的一种重要的思想方法。运用数形结合的方法,可以帮助理解计算方法,进行计算。同时也可以探索数学规律,借此解决问题。
+ + + + + +…=
1
2
1
4
1
8
1
16
1
32
1
64
1
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
2022秋 人教数学
六年级上册
8 数学广角——数与形
通过自主探究发现图形中隐藏着的数的规律,并会应用所发现的规律。 (重点)
2. 会利用图形来解决一些有关数的问题。(重点)
3. 在解决问题的过程中,体会和掌握数形结合、归纳推理、极限等基本的数学思想。(难点)
学习目标
回顾复习
1+3=( )
1+3+5=( )
1+3+5+7=( )
1+3+5+7+9+…+21=( )(用计算器算一算)
计算出结果。
4
9
16
121
想一想,说一说:在刚才的计算中,你发现了什么?
算式左边是连续的奇数相加。
你能发现其中的规律吗?这节课我们学习数形结合的方法,使你能更快地发现规律,更容易地进行计算。
回顾复习
算式右边分别是2、3、4……的平方
观察一下,下面的图和算式有什么关系?把算式补充完整。(教材P105例1)
探索新知
1
1=( )2
1+3=( )2
1+3+5=( )2
1
2
3
探索新知
图示 数形结合 看作大正方形
构图过程 小正方形个数
一个正方形
1
每行每列都有1个正方形12=1
在右上角增加正方形
1+3=4
每行每列都有2个正方形22=4
探索新知
图示 数形结合 看作大正方形
构图过程 小正方形个数
(续表)
在右上角增加正方形
1+3+5
=4
每行每列都有3个正方形32=4
探索新知
发现规律:
算式左边的加数是每个正方形图左下角的小正方形和其他“ ”形图中所包含的小正方形个数之和,正好等于每个正方形图中每列小正方形个数的平方。
探索新知
你能利用规律直接写一写吗?如果有困难,可以画图来帮助。
1+3+5+7=( )2
1+3+5+7+9+11+13=( )2
=92
4
7
1+3+5+7+9+11+13+15+17
探索新知
从1开始,连续几个奇数的和,即是几的平方。
运用数形结合发现规律,即借助图形分析并观察数在运算中的规律,以形助数。
探索新知
2
计算 + + + + + +…。(教材P105例1)
1
2
1
4
1
8
1
16
1
32
1
64
你能发现什么规律?
从第二个数开始,每个数是前一个数的 。
1
2
探索新知
按顺序计算:
+ =
1
2
1
4
3
4
+ + =
1
2
1
4
7
8
1
8
+ + + =
1
2
1
4
15
16
1
8
1
16
我一个一个加下去看看,答案好像有点规律。加下去,等号右边的分数越来越接近于1。
探索新知
画图分析、数形结合
用一个圆或一条线段表示“1”。
1
4
1
2
1
8
1
16
1
32
…
探索新知
1
2
1
4
1
8
1
16
1
32
…
+ + + + + +…=
1
2
1
4
1
8
1
16
1
32
1
64
1
从两幅图中可以看出:这些分数不断加下去,总和就是1。
有些问题通过画图解决起来更直观。
探索新知
数形结合是学习数学的一种重要的思想方法。运用数形结合的方法,可以帮助理解计算方法,进行计算。同时也可以探索数学规律,借此解决问题。
随堂小练
1.请你根据例1的结论算一算。(教材P106做一做第1题)
做一做
1+3+5+7+5+3+1=( )
1+3+5+7+9+11+13+11+9+7+5+3+1=( )
42
32
42+32
=25
72
62
85
随堂小练
2.下面每个图中各有多少个绿色小正方形和多少个蓝色小正方形?。(教材P106做一做第2题)
做一做
绿色:
1
2
3
4
蓝色:
8
10
12
14
随堂小练
从图中可以看出,第n个图形一共有3×(n+2)=3n+6个小正方形,其中有n块是绿色,3n+6-n=2n+6(块)是蓝色。
照这样接着画下去,第6个图形有多少个绿色小正方形和多少个蓝色小正方形?第10个图形呢?你能解释这其中的道理吗?
随堂小练
所以,第6个图形有6个绿色小正方形和18个蓝色小正方形;第10个图形有10个绿色小正方形和26个蓝色小正方形。
照这样接着画下去,第6个图形有多少个绿色小正方形和多少个蓝色小正方形?第10个图形呢?你能解释这其中的道理吗?
随堂小练
3.计算。
1- - - - =
1
2
1
4
1
8
1
16
1
16
1- - - - - … =
1
2
1
4
1
8
1
16
0
随堂小练
4.阳阳从家出发,骑车0.5时到达离家4 km的书店,在书店买书0.5时后步行回家,在步行2 km后遇到同学,与同学聊天0.5时,然后回家。图( )描述了阳阳的活动行程。
A
1.下面每个图中最外圈各有多少个小正方形?(教材P107练习二十二第1题)
当堂检测
32-1=8
52-32=16
72-52=24
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?你能解释其中的道理吗?
当堂检测
从图中可以看出,第n个图形的边长为2n+1,次外圈的边长(也就是上一个图形的边长)为2n-1,则第n个图形最外圈有(2n+1)2-(2n-1)2个小正方形。
当堂检测
所以第5个图形最外圈有:
(2×5+1)2-(2×5-1)2=112-92=40(个)小正方形。
2.(教材P107 练习二十二第2题)
当堂检测
1
3
6
10
请你根据上面图形与数的规律接着画一画,填一填。
15
21
28
2.(教材P107 练习二十二第2题)
当堂检测
1
3
6
10
如果不画,这样排列下去,第10个数是多少?
1+2+3+4+5+6+7+8+9+10=55
3.小林、小强、小丽、小兵和小刚5人进行象棋比赛,每两人之间都要下一盘。小林已经下了4盘,小强下了3盘,小丽下了2盘,小兵下了1盘。小刚一共下了几盘?分别和谁下的?(教材P109 练习二十二第6题)
当堂检测
用连线的方法试试。
3.小林、小强、小丽、小兵和小刚5人进行象棋比赛,每两人之间都要下一盘。小林已经下了4盘,小强下了3盘,小丽下了2盘,小兵下了1盘。小刚一共下了几盘?分别和谁下的?(教材P109 练习二十二第6题)
当堂检测
所以小刚一共下了2盘,分别是和小林、小强下的。
当堂检测
4.我国宋代数学家杨辉在1261年撰写了《详解九章算法》,他在这本著作中画了一个由数构成的三角形图,我们把它称为“杨辉三角”。你能发现右面“杨辉三角”图中各数之间的关系吗 你能按照发现的规律把这个三角形图继续写下去吗 试试看。(教材P109 练习二十二第7题)
每个数字是上一行的左右两个数字之和。继续写下去,下一行是:1 6 15 20 15 6 1 。
学习完本节课,你有什么收获?
课堂小结
课堂小结
从1开始,连续几个奇数的和,即是几的平方。
数形结合是学习数学的一种重要的思想方法。运用数形结合的方法,可以帮助理解计算方法,进行计算。同时也可以探索数学规律,借此解决问题。
+ + + + + +…=
1
2
1
4
1
8
1
16
1
32
1
64
1
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
