(2022新课标新教材)6.3 梯形的面积 课件(共25张PPT)
文档属性
| 名称 | (2022新课标新教材)6.3 梯形的面积 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-24 14:39:44 | ||
图片预览







文档简介
(共25张PPT)
2022秋 人教数学
五年级上册
6 多边形的面积
6.3 梯形的面积
1.掌握梯形的面积计算公式,并能正确计算梯形的面积。(重点)
2.通过类比和转化的方法,自主探究梯形的面积计算公式。(难点)
3.通过操作、观察和比较,培养想象力和思考力,发展空间观念,感受数学与生活的紧密联系,提高学习数学的兴趣。
学习目标
情境导入
一堆圆木的横截面如图所示,可以看作一个什么图形?拿下最上层的一根后,可以看作一个什么图形?
三角形
梯形
(教材P93)
探索新知
梯形的面积
车窗玻璃的形状是梯形,怎样计算它的面积?
你能用学过的方法推导出梯形的面积计算公式吗?
(教材P93)
探索新知
梯形的面积
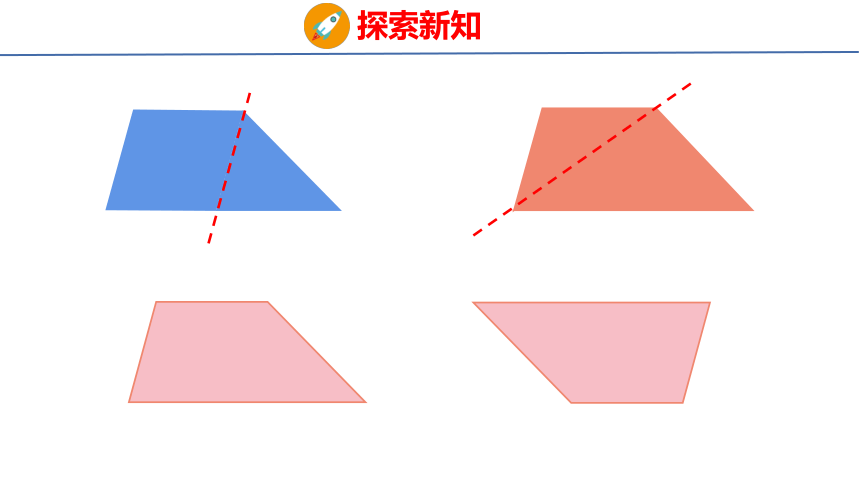
我把一个梯形剪成了两个三角形。
可以剪出一个平行四边形和一个三角形。
两个同样的梯形可以拼成一个平行四边形。
探索新知
探索新知
高
下底
观察拼成的平行四边形和原来的梯形,你发现了什么?
平行四边形的底相当于梯形的( ),平行四边形的高相当于梯形的( )。
上底与下底之和
高
上底
如果用S表示梯形的面积,
用a、b和h分别表示梯形的上底、下底和高,
那么梯形的面积计算公式可以写成:
__________________
探索新知
梯形的面积=________________________
(上底+下底)×高÷2
S=(a+b)h÷2
h
a
b
探索新知
我国三峡水电站大坝的横截面是梯形(如下图),求它的面积。
S=(a+b)h÷2
=(36+120)×135÷2
=156×135÷2
=10530(m2)
3
(教材P94)
120 m
36 m
135 m
探索新知
归纳总结:
梯形面积=(上底+下底)×高÷2,
用字母表示梯形的面积计算公式为:
S=(a+b)h÷2
1.一辆汽车侧面的两块玻璃的形状是梯形(如下图),它们的面积分别是多少?(教材P94做一做 )
(40+71)×40÷2=2220(cm2)
随堂小练
做一做
71 cm
40 cm
65 cm
40 cm
45 cm
(45+65)×40÷2=2200(cm2)
2.一条新挖的水渠,横截面是梯形(如图)。渠口宽2.8 m,渠底宽1.4 m,渠深1.2 m。横截面的面积是多少平方米?(教材P95练习二十一 第1题)
随堂小练
答:横截面的面积是2.52 m2。
2.8 m
1.4 m
1.2 m
(1.4+2.8)×1.2÷2
=2.52(m2)
3.寻找合适的条件,计算出下图中涂色梯形的面积。(单位:cm)(教材P95练习二十一 第5题)
随堂小练
18
9
12
2.3
5
3.4
2.2
4.8
7.2
1.6
3.寻找合适的条件,计算出下图中涂色梯形的面积。(单位:cm)(教材P95练习二十一 第5题)
随堂小练
18
9
12
(18+12)×9÷2=135(cm2)
3.寻找合适的条件,计算出下图中涂色梯形的面积。(单位:cm)(教材P95练习二十一 第5题)
随堂小练
2.3
5
3.4
(5-2.3+5)×3.4÷2=13.09(cm2)
5×3.4-2.3×3.4÷2=13.09(cm2)
3.寻找合适的条件,计算出下图中涂色梯形的面积。(单位:cm)(教材P95练习二十一 第5题)
随堂小练
2.2
4.8
7.2
1.6
(7.2-1.6-2.2+7.2)×4.8÷2
=25.44(cm2)
7.2×4.8-1.6×4.8÷2-2.2×4.8÷2
=13.09(cm2)
1.靠墙边围成一个梯形花坛,围花坛的篱笆长46 m,求这个花坛的面积。(教材P96练习二十一 第6题)
当堂检测
(46-20)×20÷2=260(m2)
答:这个花坛的面积是260 m2。
20 m
2.已知一个梯形的面积是15 cm2。它的上底是4.5 cm,高是3 cm,下底是多少厘米?(列方程解决。)
(教材P96练习二十一 第7题)
当堂检测
解:设下底是xcm。
(4.5+x)×3÷2=15
x=5.5
答:下底是5.5 cm。
3.生活中圆木、钢管等经常像下图这样堆放,这样就可以用下面的方法求总根数: (教材P96练习二十一 第7题)
当堂检测
(顶层根数+底层根数)×层数÷2
计算图中圆木的总根数。
(2+6)×5÷2 =20(根)
答:图中圆木的总根数是20根。
4.(易错题)一个梯形的高扩大到原来的3倍,上底和下底都扩大到原来的3倍,它的面积扩大到原来的( )倍。
A. 3 B. 6 C. 9 D. 27
当堂检测
C
反思:高不变,梯形的上底和下底都扩大到原来的
m倍,面积就扩大到原来的m倍;
如果高也同时扩大到原来n倍,面积扩大到原来的mn倍。
5.填空:
(1)一个梯形的面积是45 cm2,上底与下底的和是9 cm,那么它的高是( )cm。
(2)一个梯形的面积是28 dm2,如果上底增加3 dm,下底减少3 dm,高扩大到原来的2.3倍,那么新梯形的面积是( )dm2。
当堂检测
10
6.44
学习完本节课,你有什么收获?
课堂小结
课堂小结
1.梯形面积=(上底+下底)×高÷2。 S=(a+b)h÷2
2.梯形的上底=梯形的面积×2÷高-下底 a=2S÷h-b
梯形的下底=梯形的面积×2÷高-上底 b=2S÷h-a
梯形的高=梯形的面积×2÷(上底+下底)
h=2S÷(a+b)
3.堆成梯形形状的圆木总根数的计算方法:
(顶层根数+底层根数)×层数÷2
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
2022秋 人教数学
五年级上册
6 多边形的面积
6.3 梯形的面积
1.掌握梯形的面积计算公式,并能正确计算梯形的面积。(重点)
2.通过类比和转化的方法,自主探究梯形的面积计算公式。(难点)
3.通过操作、观察和比较,培养想象力和思考力,发展空间观念,感受数学与生活的紧密联系,提高学习数学的兴趣。
学习目标
情境导入
一堆圆木的横截面如图所示,可以看作一个什么图形?拿下最上层的一根后,可以看作一个什么图形?
三角形
梯形
(教材P93)
探索新知
梯形的面积
车窗玻璃的形状是梯形,怎样计算它的面积?
你能用学过的方法推导出梯形的面积计算公式吗?
(教材P93)
探索新知
梯形的面积
我把一个梯形剪成了两个三角形。
可以剪出一个平行四边形和一个三角形。
两个同样的梯形可以拼成一个平行四边形。
探索新知
探索新知
高
下底
观察拼成的平行四边形和原来的梯形,你发现了什么?
平行四边形的底相当于梯形的( ),平行四边形的高相当于梯形的( )。
上底与下底之和
高
上底
如果用S表示梯形的面积,
用a、b和h分别表示梯形的上底、下底和高,
那么梯形的面积计算公式可以写成:
__________________
探索新知
梯形的面积=________________________
(上底+下底)×高÷2
S=(a+b)h÷2
h
a
b
探索新知
我国三峡水电站大坝的横截面是梯形(如下图),求它的面积。
S=(a+b)h÷2
=(36+120)×135÷2
=156×135÷2
=10530(m2)
3
(教材P94)
120 m
36 m
135 m
探索新知
归纳总结:
梯形面积=(上底+下底)×高÷2,
用字母表示梯形的面积计算公式为:
S=(a+b)h÷2
1.一辆汽车侧面的两块玻璃的形状是梯形(如下图),它们的面积分别是多少?(教材P94做一做 )
(40+71)×40÷2=2220(cm2)
随堂小练
做一做
71 cm
40 cm
65 cm
40 cm
45 cm
(45+65)×40÷2=2200(cm2)
2.一条新挖的水渠,横截面是梯形(如图)。渠口宽2.8 m,渠底宽1.4 m,渠深1.2 m。横截面的面积是多少平方米?(教材P95练习二十一 第1题)
随堂小练
答:横截面的面积是2.52 m2。
2.8 m
1.4 m
1.2 m
(1.4+2.8)×1.2÷2
=2.52(m2)
3.寻找合适的条件,计算出下图中涂色梯形的面积。(单位:cm)(教材P95练习二十一 第5题)
随堂小练
18
9
12
2.3
5
3.4
2.2
4.8
7.2
1.6
3.寻找合适的条件,计算出下图中涂色梯形的面积。(单位:cm)(教材P95练习二十一 第5题)
随堂小练
18
9
12
(18+12)×9÷2=135(cm2)
3.寻找合适的条件,计算出下图中涂色梯形的面积。(单位:cm)(教材P95练习二十一 第5题)
随堂小练
2.3
5
3.4
(5-2.3+5)×3.4÷2=13.09(cm2)
5×3.4-2.3×3.4÷2=13.09(cm2)
3.寻找合适的条件,计算出下图中涂色梯形的面积。(单位:cm)(教材P95练习二十一 第5题)
随堂小练
2.2
4.8
7.2
1.6
(7.2-1.6-2.2+7.2)×4.8÷2
=25.44(cm2)
7.2×4.8-1.6×4.8÷2-2.2×4.8÷2
=13.09(cm2)
1.靠墙边围成一个梯形花坛,围花坛的篱笆长46 m,求这个花坛的面积。(教材P96练习二十一 第6题)
当堂检测
(46-20)×20÷2=260(m2)
答:这个花坛的面积是260 m2。
20 m
2.已知一个梯形的面积是15 cm2。它的上底是4.5 cm,高是3 cm,下底是多少厘米?(列方程解决。)
(教材P96练习二十一 第7题)
当堂检测
解:设下底是xcm。
(4.5+x)×3÷2=15
x=5.5
答:下底是5.5 cm。
3.生活中圆木、钢管等经常像下图这样堆放,这样就可以用下面的方法求总根数: (教材P96练习二十一 第7题)
当堂检测
(顶层根数+底层根数)×层数÷2
计算图中圆木的总根数。
(2+6)×5÷2 =20(根)
答:图中圆木的总根数是20根。
4.(易错题)一个梯形的高扩大到原来的3倍,上底和下底都扩大到原来的3倍,它的面积扩大到原来的( )倍。
A. 3 B. 6 C. 9 D. 27
当堂检测
C
反思:高不变,梯形的上底和下底都扩大到原来的
m倍,面积就扩大到原来的m倍;
如果高也同时扩大到原来n倍,面积扩大到原来的mn倍。
5.填空:
(1)一个梯形的面积是45 cm2,上底与下底的和是9 cm,那么它的高是( )cm。
(2)一个梯形的面积是28 dm2,如果上底增加3 dm,下底减少3 dm,高扩大到原来的2.3倍,那么新梯形的面积是( )dm2。
当堂检测
10
6.44
学习完本节课,你有什么收获?
课堂小结
课堂小结
1.梯形面积=(上底+下底)×高÷2。 S=(a+b)h÷2
2.梯形的上底=梯形的面积×2÷高-下底 a=2S÷h-b
梯形的下底=梯形的面积×2÷高-上底 b=2S÷h-a
梯形的高=梯形的面积×2÷(上底+下底)
h=2S÷(a+b)
3.堆成梯形形状的圆木总根数的计算方法:
(顶层根数+底层根数)×层数÷2
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
