(2022新课标新教材)人教版五年级数学上册5.14 实际问题与方程(5) 课件(共23张PPT)
文档属性
| 名称 | (2022新课标新教材)人教版五年级数学上册5.14 实际问题与方程(5) 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 11.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-24 15:12:41 | ||
图片预览







文档简介
(共23张PPT)
2022秋 人教数学
五年级上册
5 简易方程
5.14 实际问题与方程(5)
1.学会用画线段图等方法直观、清晰地分析数量关系,结合具体情境列方程解决相遇问题。(重点)
2.培养初步的逻辑推理能力和解决稍复杂的行程问题的能力,提高分析问题和解决问题的能力。(难点)
3.激发学习兴趣,培养抽象思维能力,体会数学的应用价值。
学习目标
回顾复习
路程公式:路程=速度×时间
相遇问题:
甲的速度×甲用的时间+乙的速度×乙用的时间=总路程
(甲的速度+乙的速度)×相遇时间=总路程
相离问题:
甲的速度×甲用的时间+乙的速度×乙用的时间=总路程
追及问题:
快的速度×对应时间-慢的速度×对应时间=相隔的距离
(教材P78 例10)
探索新知
小云家和小林家相距4.5 km。周日早上9:00两人分别从家骑自行车相向而行,两人何时相遇?
10
我每分钟骑200 m。
我每分钟骑250 m。
探索新知
阅读与理解
知道了……
要解决的问题是……
总路程是4.5 km,
小云的骑行速度每分钟200 m,
小林的骑行速度每分钟250 m。
两人何时相遇,
即求相遇时间。
探索新知
分析与解答
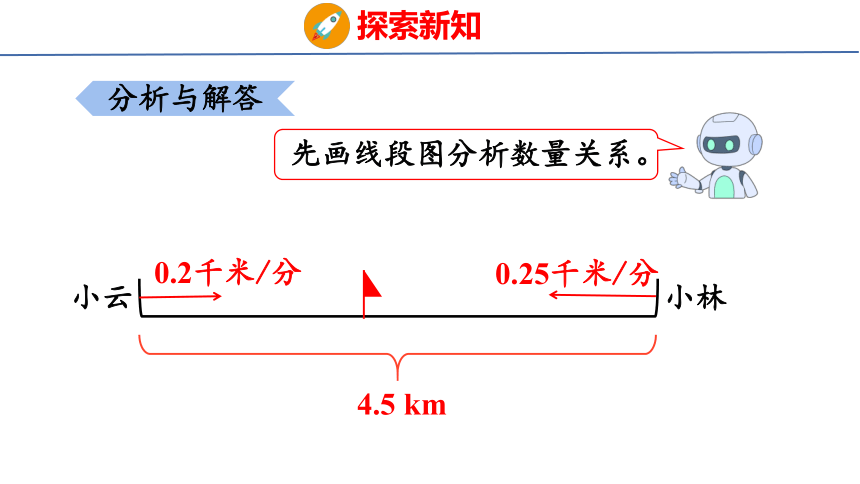
先画线段图分析数量关系。
4.5 km
0.2千米/分
小林
小云
0.25千米/分
探索新知
分析与解答
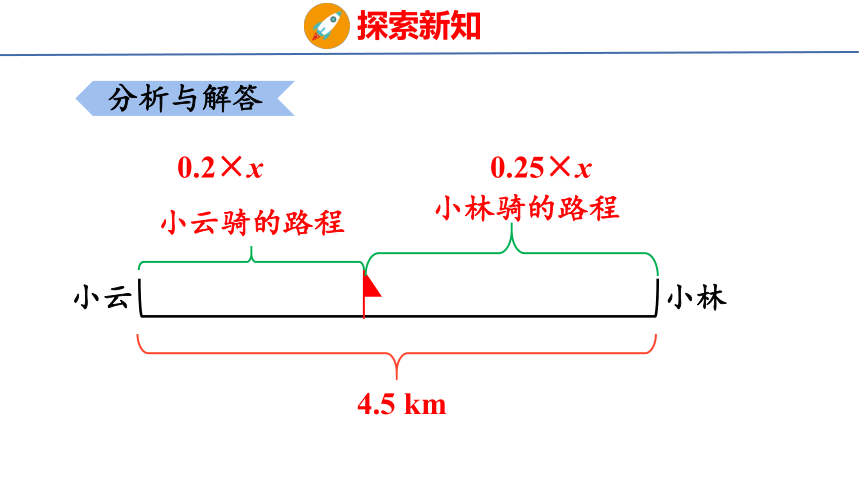
4.5 km
小林
小云
小林骑的路程
小云骑的路程
0.2×x
0.25×x
探索新知
分析与解答
解:设两人x分钟后相遇。
小云骑的路程+小林骑的路程=总路程
0.2x+0.25x=4.5
x=10
0.45x=4.5
0.45x÷0.45=4.5÷0.45
答:两人__________相遇。
10分钟后
还可以怎样列方程?
探索新知
分析与解答
解:设两人x分钟后相遇。
两人每分钟骑行的路程和×相遇时间=总路程
(0.2+0.25)x=4.5
x=10
0.45x=4.5
0.45x÷0.45=4.5÷0.45
答:两人10分钟后相遇。
探索新知
回顾与反思
这里要用到速度、时间和路程的数量关系来列方程。
通过画线段图可以清楚地分析数量之间的相等关系。
探索新知
归纳总结:
1.相遇问题的基本特征:
两个物体同时由两地出发,相向而行,在途中相遇。
2.相遇问题的基本关系:
甲行的路程+乙行的路程=总路程
或甲乙速度和×相遇时间=总路程
1. 两列火车从相距600 km的两地同时相向开出。甲车每小时行驶230 km,乙车每小时行驶170 km。经过几个小时两车相遇?(教材P80练习十七 第9题)
解:设经过x小时两车相遇。
答:经过1.5小时两车相遇。
(230+170)x=600
x=1.5
还可以怎样列方程?
230x+170x=600
x=1.5
随堂小练
2.两地间的路程是455 km。甲乙两辆汽车同时从两地开出,相向而行,经过3.5小时相遇。甲车每小时行驶68 km,乙车每小时行驶多少千米?(教材P80练习十七 第10题)
答:乙车每小时行驶62千米。
解:设乙车每小时行驶x千米。
(68+x)×3.5=455
x=62
68×3.5+3.5x=455
x=62
随堂小练
3.甲乙两艘轮船同时从A地出发开往B地。经过18小时后,甲船落后乙船57.6 km。甲船每小时行驶32.5 km,乙船每小时行驶多少千米?(教材P80练习十七 第11题)
A地
B地
A地
57.6 km
甲船
乙船
随堂小练
3.甲乙两艘轮船同时从A地出发开往B地。经过18小时后,甲船落后乙船57.6 km。甲船每小时行驶32.5 km,乙船每小时行驶多少千米?(教材P80练习十七 第11题)
答:乙船每小时行驶35.7千米。
解:设乙船每小时行驶x千米。
18x-32.5×18=57.6
x=35.7
(x-32.5)×18=57.6
x=35.7
随堂小练
当堂检测
1.在下面的两个 里填入相同的数,使等式成立。
(教材P80练习十七 第12题)
24× - ×15=18
2
2
2.一辆汽车和一辆货车同时从两地开出,相向而行。货车每小时行驶36 km,汽车每小时行驶40 km,x小时后相遇。两地相距( )km。
A.36x B.40x
C.(36+40)x D.40x-36x
当堂检测
C
3.甲、乙两村同时合挖一条1500 m长的水渠,分别从两端开始相向施工,20天完成。甲村每天挖的长度是乙村的1.5倍。甲、乙两村每天各挖多少米?
当堂检测
解:设乙村每天挖x m,那么甲村每天挖1.5x m。
答:甲村每天挖45 m,乙村每天挖30 m。
(1.5x+x)×20=1500
x=30
1.5x=1.5×30=45
4.两地相距280 km。甲、乙两车同时从两地出发,相向而行。甲车每小时行驶60 km,2.5小时后两车相距7.5 km。乙车每小时行驶多少千米?
当堂检测
解:设乙车每小时行驶x km。
x=49
(60+x)×2.5=280-7.5
情况一:
x=55
(60+x)×2.5=280+7.5
情况二:
答:乙车每小时行驶49 km或 55km。
学习完本节课,你有什么收获?
课堂小结
课堂小结
列方程解决相遇问题,可以根据“甲行驶的路程+乙行驶的路程=总路程”或“单位时间内甲乙共行驶的路程×相遇时间=总路程”列方程求解。
一般列形如ax+bx=c或(a+b)x=c的方程求解。
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
2022秋 人教数学
五年级上册
5 简易方程
5.14 实际问题与方程(5)
1.学会用画线段图等方法直观、清晰地分析数量关系,结合具体情境列方程解决相遇问题。(重点)
2.培养初步的逻辑推理能力和解决稍复杂的行程问题的能力,提高分析问题和解决问题的能力。(难点)
3.激发学习兴趣,培养抽象思维能力,体会数学的应用价值。
学习目标
回顾复习
路程公式:路程=速度×时间
相遇问题:
甲的速度×甲用的时间+乙的速度×乙用的时间=总路程
(甲的速度+乙的速度)×相遇时间=总路程
相离问题:
甲的速度×甲用的时间+乙的速度×乙用的时间=总路程
追及问题:
快的速度×对应时间-慢的速度×对应时间=相隔的距离
(教材P78 例10)
探索新知
小云家和小林家相距4.5 km。周日早上9:00两人分别从家骑自行车相向而行,两人何时相遇?
10
我每分钟骑200 m。
我每分钟骑250 m。
探索新知
阅读与理解
知道了……
要解决的问题是……
总路程是4.5 km,
小云的骑行速度每分钟200 m,
小林的骑行速度每分钟250 m。
两人何时相遇,
即求相遇时间。
探索新知
分析与解答
先画线段图分析数量关系。
4.5 km
0.2千米/分
小林
小云
0.25千米/分
探索新知
分析与解答
4.5 km
小林
小云
小林骑的路程
小云骑的路程
0.2×x
0.25×x
探索新知
分析与解答
解:设两人x分钟后相遇。
小云骑的路程+小林骑的路程=总路程
0.2x+0.25x=4.5
x=10
0.45x=4.5
0.45x÷0.45=4.5÷0.45
答:两人__________相遇。
10分钟后
还可以怎样列方程?
探索新知
分析与解答
解:设两人x分钟后相遇。
两人每分钟骑行的路程和×相遇时间=总路程
(0.2+0.25)x=4.5
x=10
0.45x=4.5
0.45x÷0.45=4.5÷0.45
答:两人10分钟后相遇。
探索新知
回顾与反思
这里要用到速度、时间和路程的数量关系来列方程。
通过画线段图可以清楚地分析数量之间的相等关系。
探索新知
归纳总结:
1.相遇问题的基本特征:
两个物体同时由两地出发,相向而行,在途中相遇。
2.相遇问题的基本关系:
甲行的路程+乙行的路程=总路程
或甲乙速度和×相遇时间=总路程
1. 两列火车从相距600 km的两地同时相向开出。甲车每小时行驶230 km,乙车每小时行驶170 km。经过几个小时两车相遇?(教材P80练习十七 第9题)
解:设经过x小时两车相遇。
答:经过1.5小时两车相遇。
(230+170)x=600
x=1.5
还可以怎样列方程?
230x+170x=600
x=1.5
随堂小练
2.两地间的路程是455 km。甲乙两辆汽车同时从两地开出,相向而行,经过3.5小时相遇。甲车每小时行驶68 km,乙车每小时行驶多少千米?(教材P80练习十七 第10题)
答:乙车每小时行驶62千米。
解:设乙车每小时行驶x千米。
(68+x)×3.5=455
x=62
68×3.5+3.5x=455
x=62
随堂小练
3.甲乙两艘轮船同时从A地出发开往B地。经过18小时后,甲船落后乙船57.6 km。甲船每小时行驶32.5 km,乙船每小时行驶多少千米?(教材P80练习十七 第11题)
A地
B地
A地
57.6 km
甲船
乙船
随堂小练
3.甲乙两艘轮船同时从A地出发开往B地。经过18小时后,甲船落后乙船57.6 km。甲船每小时行驶32.5 km,乙船每小时行驶多少千米?(教材P80练习十七 第11题)
答:乙船每小时行驶35.7千米。
解:设乙船每小时行驶x千米。
18x-32.5×18=57.6
x=35.7
(x-32.5)×18=57.6
x=35.7
随堂小练
当堂检测
1.在下面的两个 里填入相同的数,使等式成立。
(教材P80练习十七 第12题)
24× - ×15=18
2
2
2.一辆汽车和一辆货车同时从两地开出,相向而行。货车每小时行驶36 km,汽车每小时行驶40 km,x小时后相遇。两地相距( )km。
A.36x B.40x
C.(36+40)x D.40x-36x
当堂检测
C
3.甲、乙两村同时合挖一条1500 m长的水渠,分别从两端开始相向施工,20天完成。甲村每天挖的长度是乙村的1.5倍。甲、乙两村每天各挖多少米?
当堂检测
解:设乙村每天挖x m,那么甲村每天挖1.5x m。
答:甲村每天挖45 m,乙村每天挖30 m。
(1.5x+x)×20=1500
x=30
1.5x=1.5×30=45
4.两地相距280 km。甲、乙两车同时从两地出发,相向而行。甲车每小时行驶60 km,2.5小时后两车相距7.5 km。乙车每小时行驶多少千米?
当堂检测
解:设乙车每小时行驶x km。
x=49
(60+x)×2.5=280-7.5
情况一:
x=55
(60+x)×2.5=280+7.5
情况二:
答:乙车每小时行驶49 km或 55km。
学习完本节课,你有什么收获?
课堂小结
课堂小结
列方程解决相遇问题,可以根据“甲行驶的路程+乙行驶的路程=总路程”或“单位时间内甲乙共行驶的路程×相遇时间=总路程”列方程求解。
一般列形如ax+bx=c或(a+b)x=c的方程求解。
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
