安徽省滁州市定远县民族中学2022-2023学年高三上学期9月开学检测数学试题(Word版含答案)
文档属性
| 名称 | 安徽省滁州市定远县民族中学2022-2023学年高三上学期9月开学检测数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 656.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 12:52:43 | ||
图片预览




文档简介
定远县民族中学2022-2023学年高三上学期9月开学检测
数学试题
第I卷 选择题(共60分)
一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.已知集合,,则( )
A. B. C. D.
2.已知为的共轭复数,若,则
A. B. C. D.
3.已知等比数列满足: ,且是的等差中项.则
A.或 B. C.或 D.
4.不等式组所表示的平面区域的面积为
A. B. C. D.
5.y1=40.9,y2=log4.3,y3=()1.5,则( )
A.y3>y1>y2 B.y2>y1>y3
C.y1>y2>y3 D.y1>y3>y2
6.“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.已知是的内角,且,则的值为( )
A.-1或7 B.或1 C.-1 D.
8.如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )
A. B. C. D.4
9.若,,则( )
A. B. C. D.
10.《九章算术·商功》:“斜解立方,得两堑堵,斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以基,其形露矣.”文中“阳马”是底面为长方形且有一条侧棱与底面垂直的四棱锥.在阳马中,侧棱底面,且,,则点到平面的距离为( )
A. B. C. D.
11.角谷猜想,也叫猜想,是由日本数学家角谷静夫发现的,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2,如此循环最终都能够得到1,如:取,根据上述过程,得出10,5,16,8,4,2,1,共7个数.上述过程得到的7个整数中,随机选取两个不同的数,则两个数都是奇数的概率为( ).
A. B. C. D.
12.定义在上的函数满足,且当时,.若关于的方程在上至少有两个实数解,则实数的取值范围为
A. B. C. D.
第II卷 非选择题(共90分)
二、填空题(本大题共4小题,每小题5分,共20分)
13.直线,,若,则求_______________.
14.已知函数,若关于的不等式恒成立,则实数的取值范围是__________.
15.二项式展开式中的常数项为240,则实数的值为________.
16.已知函数,,若方程有三个不同实数解,,,且它们可以构成等差数列,则______.
三、解答题(本大题共6小题,共70分。其中22、23为选考题。解答应写出文字说明、证明过程或演算步骤。)
17.(12分)中,内角,,所对边分别为,,,且.
(1)求角的大小;
(2)若,且,求的面积.
18.(12分)为推动实施健康中国战略,树立国家大卫生 大健康概念,手机也推出了多款健康运动软件,如“微信运动”.张先生的微信朋友圈内有位好友参与了“微信运动”,他随机选取了位微信好友(女人,男人),统计其在某一天的走路步数.其中,女性好友的走路步数数据记录如下:
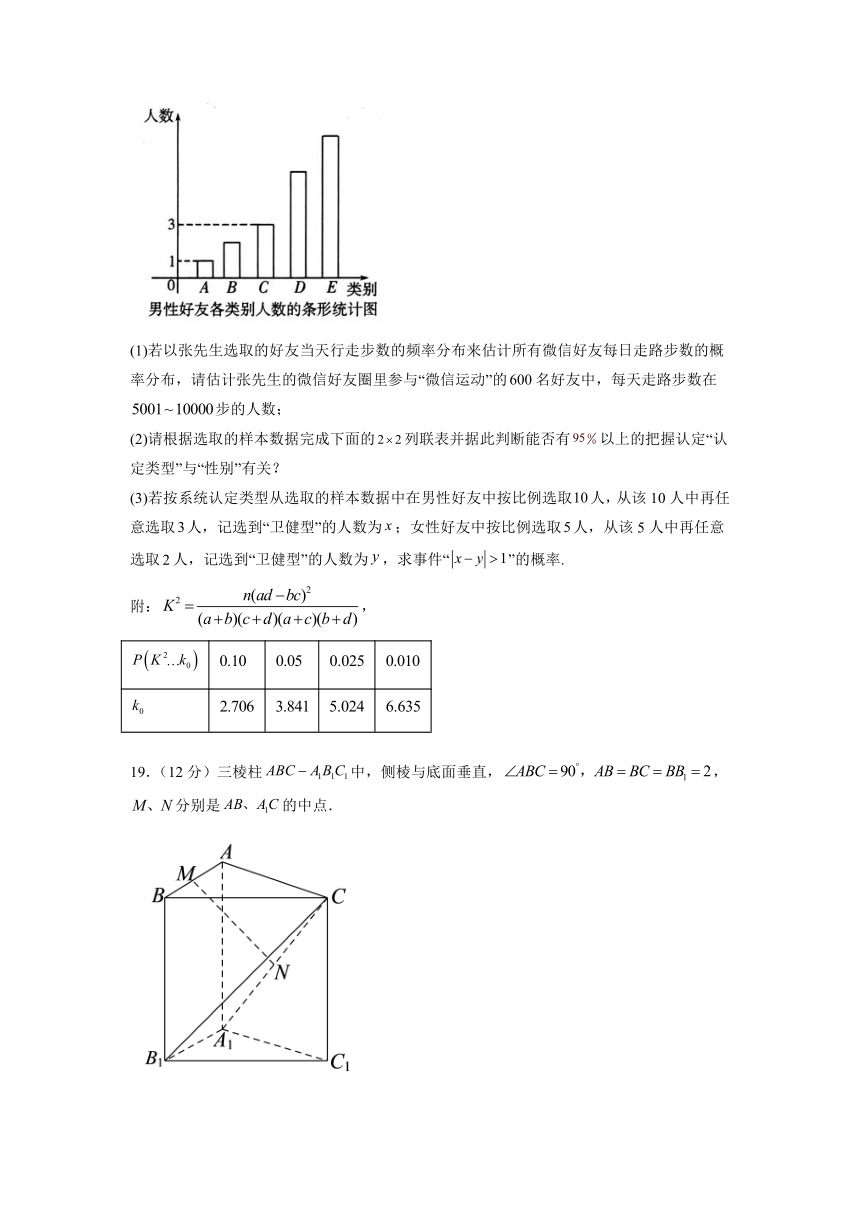
男性好友走路的步数情况可分为五个类别:(步(说明:“”表示大于等于0,小于等于2000,下同),(步),(步),(步),(步及以上),且三种类别入数比例为,将统计结果绘制如图所示的条形图.若某人一天的走路步数超过步被系统认定为“卫健型”,否则被系统认定为“进步型”.
卫健型 进步型 总计
男 20
女 20
总计 40
(1)若以张先生选取的好友当天行走步数的频率分布来估计所有微信好友每日走路步数的概率分布,请估计张先生的微信好友圈里参与“微信运动”的名好友中,每天走路步数在步的人数;
(2)请根据选取的样本数据完成下面的列联表并据此判断能否有以上的把握认定“认定类型”与“性别”有关?
(3)若按系统认定类型从选取的样本数据中在男性好友中按比例选取人,从该10人中再任意选取人,记选到“卫健型”的人数为;女性好友中按比例选取人,从该5人中再任意选取人,记选到“卫健型”的人数为,求事件“”的概率.
附:,
19.(12分)三棱柱中,侧棱与底面垂直,,分别是的中点.
(1)求证:平面;
(2)求证:平面;
(3)求三棱锥的体积.
20.(12分)已知函数.
(Ⅰ)若函数在处的切线方程为,求和的值;
(Ⅱ)讨论方程的解的个数,并说明理由.
21.(12分)已知离心率为的椭圆与x轴,y轴正半轴交于A,B两点,作直线AB的平行线交椭圆于C,D两点.
(1)若△AOB的面积为1,求椭圆的标准方程;
(2)在(1)的条件下,
(i)记直线AC,BD的斜率分别为,,求证:为定值;
(ii)求|CD|的最大值.
22.(10分)选修4 - 4:坐标系与参数方程
在平面直角坐标系xOy中,直线l的参数方程为(t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为.
(1)求直线l的一般式方程和曲线C的标准方程;
(2)若直线l与曲线C交于A,B两点,点,求的值.
23.(10分)选修4-5:不等式选讲
已知函数.
(1)当时,求不等式的解集;
(2)若(a,b,c均为正实数)的最小值为3,求的最小值.
参考答案
1.B 2.C 3.C 4.B 5.D 6.B 7.C 8.B 9.D 10.B 11.C 12.C
13.或
14.
15.
16.
17.(1);(2).
【解析】(1)
,
即,
∵,∴.
(2)由,可得,
由正弦定理,得,即.
由余弦定理及,
解得,,
∴的面积.
18.(1)人
(2)列联表答案见解析,没有95%以上的把握认为“认定类型”与“性别”有关
(3)
【解析】 (1)在样本数据中,男性好友B类别设为x人,则由题意可知:
,可知,故B类别有2人,D类别有6人,E类别有8人,走路步数在5001~10000步的包括C D类别两类别共计9人;女性好友走路步数在5001~10000步共有16人.
用样本数据估计所有微信好友每日走路步数的概率分布,则:人;
(2)根据题意选取的40个样本数据的列联表为:
卫健型 进步型 总计
男 14 6 20
女 8 12 20
总计 22 18 40
得:,
故没有95%以上的把握认为“认定类型”与“性别”有关;
(3)在男性好友那个“卫健型”与“进步型”的比为7:3,则选取10人,恰好选取“卫健型”7人,“进步型”3人;在女性好友中“卫健型”与“进步型”的比例为2:3,选取5人,恰好选取“卫健型”2人,“进步型”3人;
“”包含“,”,“,”,“,”,“,”,
,,
,,
故.
19.【解析】 (1)连接,∵在中,分别是的中点,
∴,又∵平面,平面,
∴平面;
(2)∵三棱柱中,侧棱与底面垂直,
∴四边形是正方形.∴,又,∴.
连接,.∴,又是的中点,
∴.又,、平面,
∴平面;
(3)由(2)知是三棱锥的高,
在直角中,,
.故.
20.(1) , .
(2)当时,方程无解;当或时,方程有唯一解;当时,方程有两解.
【解析】(Ⅰ)因为,又在处得切线方程为,
所以,解得.
(Ⅱ)当时,在定义域内恒大于0,此时方程无解.
当时,在区间内恒成立,
所以为定义域为增函数,因为,
所以方程有唯一解.
当时,.
当时,, 在区间内为减函数,
当时,,在区间内为增函数,
所以当时,取得最小值.
当时,,无方程解;
当时,,方程有唯一解.
当时,,
因为,且,所以方程在区间内有唯一解,
当时,设,所以在区间内为增函数,
又,所以,即,故.
因为,所以.
所以方程在区间内有唯一解,所以方程在区间内有两解,
综上所述,当时,方程无解.
21. 【解析】 (1)椭圆的离心率为,∴,即①.
又②,由①②解得,故椭圆的标准方程是
(2)
(i)设直线CD,代人得得,
设,
分子=
∴为定值
(ii)令直线AC:
∵
∴
∴
由韦达定理得,
故
由(1)知,直线
,故.,
从而,
记.当时,
当时,记,则
令
当时.于是.
此时,,
当且仅当即时,等号成立.
同理,当时,
此时
当且仅当即时,等号成立.
综上所述,当且仅当时,|CD|取得最大值,.
22.(1)直线l:,曲线C:
(2)
【解析】(1)直线l的参数方程为(t为参数),消去t化为一般式方程为;曲线C的极坐标方程为,由于,代入上式, 化为标准方程为;
(2)设直线l的参数方程为 (t为参数),则参数t表示直线l上的点到P点的带符号的几何距离,代入,得,由韦达定理得:,则;综上,直线l的一般方程为:,曲线C的标准方程为:,.
23.(1)或; (2)4.
【解析】
(1)当时,不等式即,
∴:,或,
∴,或,
故不等式的解集为或;
(2)由绝对值三角不等式可得:
,当且仅当时取等号,
∵均为正实数,∴,
∴根据柯西不等式可得,,
∴,当且仅当,即时等号成立,
∴的最小值是4.
数学试题
第I卷 选择题(共60分)
一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.已知集合,,则( )
A. B. C. D.
2.已知为的共轭复数,若,则
A. B. C. D.
3.已知等比数列满足: ,且是的等差中项.则
A.或 B. C.或 D.
4.不等式组所表示的平面区域的面积为
A. B. C. D.
5.y1=40.9,y2=log4.3,y3=()1.5,则( )
A.y3>y1>y2 B.y2>y1>y3
C.y1>y2>y3 D.y1>y3>y2
6.“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.已知是的内角,且,则的值为( )
A.-1或7 B.或1 C.-1 D.
8.如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )
A. B. C. D.4
9.若,,则( )
A. B. C. D.
10.《九章算术·商功》:“斜解立方,得两堑堵,斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以基,其形露矣.”文中“阳马”是底面为长方形且有一条侧棱与底面垂直的四棱锥.在阳马中,侧棱底面,且,,则点到平面的距离为( )
A. B. C. D.
11.角谷猜想,也叫猜想,是由日本数学家角谷静夫发现的,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2,如此循环最终都能够得到1,如:取,根据上述过程,得出10,5,16,8,4,2,1,共7个数.上述过程得到的7个整数中,随机选取两个不同的数,则两个数都是奇数的概率为( ).
A. B. C. D.
12.定义在上的函数满足,且当时,.若关于的方程在上至少有两个实数解,则实数的取值范围为
A. B. C. D.
第II卷 非选择题(共90分)
二、填空题(本大题共4小题,每小题5分,共20分)
13.直线,,若,则求_______________.
14.已知函数,若关于的不等式恒成立,则实数的取值范围是__________.
15.二项式展开式中的常数项为240,则实数的值为________.
16.已知函数,,若方程有三个不同实数解,,,且它们可以构成等差数列,则______.
三、解答题(本大题共6小题,共70分。其中22、23为选考题。解答应写出文字说明、证明过程或演算步骤。)
17.(12分)中,内角,,所对边分别为,,,且.
(1)求角的大小;
(2)若,且,求的面积.
18.(12分)为推动实施健康中国战略,树立国家大卫生 大健康概念,手机也推出了多款健康运动软件,如“微信运动”.张先生的微信朋友圈内有位好友参与了“微信运动”,他随机选取了位微信好友(女人,男人),统计其在某一天的走路步数.其中,女性好友的走路步数数据记录如下:
男性好友走路的步数情况可分为五个类别:(步(说明:“”表示大于等于0,小于等于2000,下同),(步),(步),(步),(步及以上),且三种类别入数比例为,将统计结果绘制如图所示的条形图.若某人一天的走路步数超过步被系统认定为“卫健型”,否则被系统认定为“进步型”.
卫健型 进步型 总计
男 20
女 20
总计 40
(1)若以张先生选取的好友当天行走步数的频率分布来估计所有微信好友每日走路步数的概率分布,请估计张先生的微信好友圈里参与“微信运动”的名好友中,每天走路步数在步的人数;
(2)请根据选取的样本数据完成下面的列联表并据此判断能否有以上的把握认定“认定类型”与“性别”有关?
(3)若按系统认定类型从选取的样本数据中在男性好友中按比例选取人,从该10人中再任意选取人,记选到“卫健型”的人数为;女性好友中按比例选取人,从该5人中再任意选取人,记选到“卫健型”的人数为,求事件“”的概率.
附:,
19.(12分)三棱柱中,侧棱与底面垂直,,分别是的中点.
(1)求证:平面;
(2)求证:平面;
(3)求三棱锥的体积.
20.(12分)已知函数.
(Ⅰ)若函数在处的切线方程为,求和的值;
(Ⅱ)讨论方程的解的个数,并说明理由.
21.(12分)已知离心率为的椭圆与x轴,y轴正半轴交于A,B两点,作直线AB的平行线交椭圆于C,D两点.
(1)若△AOB的面积为1,求椭圆的标准方程;
(2)在(1)的条件下,
(i)记直线AC,BD的斜率分别为,,求证:为定值;
(ii)求|CD|的最大值.
22.(10分)选修4 - 4:坐标系与参数方程
在平面直角坐标系xOy中,直线l的参数方程为(t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为.
(1)求直线l的一般式方程和曲线C的标准方程;
(2)若直线l与曲线C交于A,B两点,点,求的值.
23.(10分)选修4-5:不等式选讲
已知函数.
(1)当时,求不等式的解集;
(2)若(a,b,c均为正实数)的最小值为3,求的最小值.
参考答案
1.B 2.C 3.C 4.B 5.D 6.B 7.C 8.B 9.D 10.B 11.C 12.C
13.或
14.
15.
16.
17.(1);(2).
【解析】(1)
,
即,
∵,∴.
(2)由,可得,
由正弦定理,得,即.
由余弦定理及,
解得,,
∴的面积.
18.(1)人
(2)列联表答案见解析,没有95%以上的把握认为“认定类型”与“性别”有关
(3)
【解析】 (1)在样本数据中,男性好友B类别设为x人,则由题意可知:
,可知,故B类别有2人,D类别有6人,E类别有8人,走路步数在5001~10000步的包括C D类别两类别共计9人;女性好友走路步数在5001~10000步共有16人.
用样本数据估计所有微信好友每日走路步数的概率分布,则:人;
(2)根据题意选取的40个样本数据的列联表为:
卫健型 进步型 总计
男 14 6 20
女 8 12 20
总计 22 18 40
得:,
故没有95%以上的把握认为“认定类型”与“性别”有关;
(3)在男性好友那个“卫健型”与“进步型”的比为7:3,则选取10人,恰好选取“卫健型”7人,“进步型”3人;在女性好友中“卫健型”与“进步型”的比例为2:3,选取5人,恰好选取“卫健型”2人,“进步型”3人;
“”包含“,”,“,”,“,”,“,”,
,,
,,
故.
19.【解析】 (1)连接,∵在中,分别是的中点,
∴,又∵平面,平面,
∴平面;
(2)∵三棱柱中,侧棱与底面垂直,
∴四边形是正方形.∴,又,∴.
连接,.∴,又是的中点,
∴.又,、平面,
∴平面;
(3)由(2)知是三棱锥的高,
在直角中,,
.故.
20.(1) , .
(2)当时,方程无解;当或时,方程有唯一解;当时,方程有两解.
【解析】(Ⅰ)因为,又在处得切线方程为,
所以,解得.
(Ⅱ)当时,在定义域内恒大于0,此时方程无解.
当时,在区间内恒成立,
所以为定义域为增函数,因为,
所以方程有唯一解.
当时,.
当时,, 在区间内为减函数,
当时,,在区间内为增函数,
所以当时,取得最小值.
当时,,无方程解;
当时,,方程有唯一解.
当时,,
因为,且,所以方程在区间内有唯一解,
当时,设,所以在区间内为增函数,
又,所以,即,故.
因为,所以.
所以方程在区间内有唯一解,所以方程在区间内有两解,
综上所述,当时,方程无解.
21. 【解析】 (1)椭圆的离心率为,∴,即①.
又②,由①②解得,故椭圆的标准方程是
(2)
(i)设直线CD,代人得得,
设,
分子=
∴为定值
(ii)令直线AC:
∵
∴
∴
由韦达定理得,
故
由(1)知,直线
,故.,
从而,
记.当时,
当时,记,则
令
当时.于是.
此时,,
当且仅当即时,等号成立.
同理,当时,
此时
当且仅当即时,等号成立.
综上所述,当且仅当时,|CD|取得最大值,.
22.(1)直线l:,曲线C:
(2)
【解析】(1)直线l的参数方程为(t为参数),消去t化为一般式方程为;曲线C的极坐标方程为,由于,代入上式, 化为标准方程为;
(2)设直线l的参数方程为 (t为参数),则参数t表示直线l上的点到P点的带符号的几何距离,代入,得,由韦达定理得:,则;综上,直线l的一般方程为:,曲线C的标准方程为:,.
23.(1)或; (2)4.
【解析】
(1)当时,不等式即,
∴:,或,
∴,或,
故不等式的解集为或;
(2)由绝对值三角不等式可得:
,当且仅当时取等号,
∵均为正实数,∴,
∴根据柯西不等式可得,,
∴,当且仅当,即时等号成立,
∴的最小值是4.
同课章节目录
