鲁教版(五四学制)初中八年级下册8.2用配方法解一元二次方程(2) 课件(共19张PPT)
文档属性
| 名称 | 鲁教版(五四学制)初中八年级下册8.2用配方法解一元二次方程(2) 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 17:56:46 | ||
图片预览

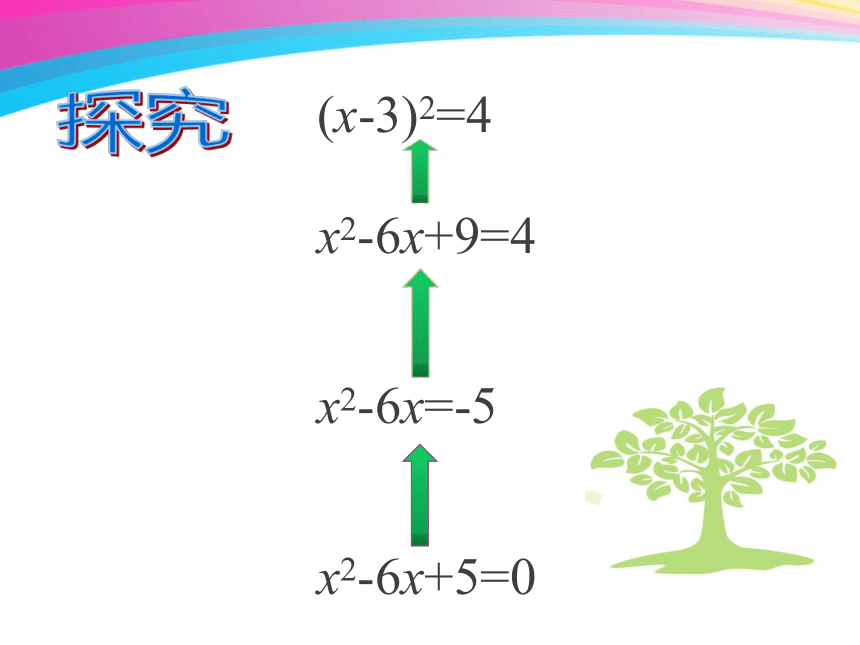
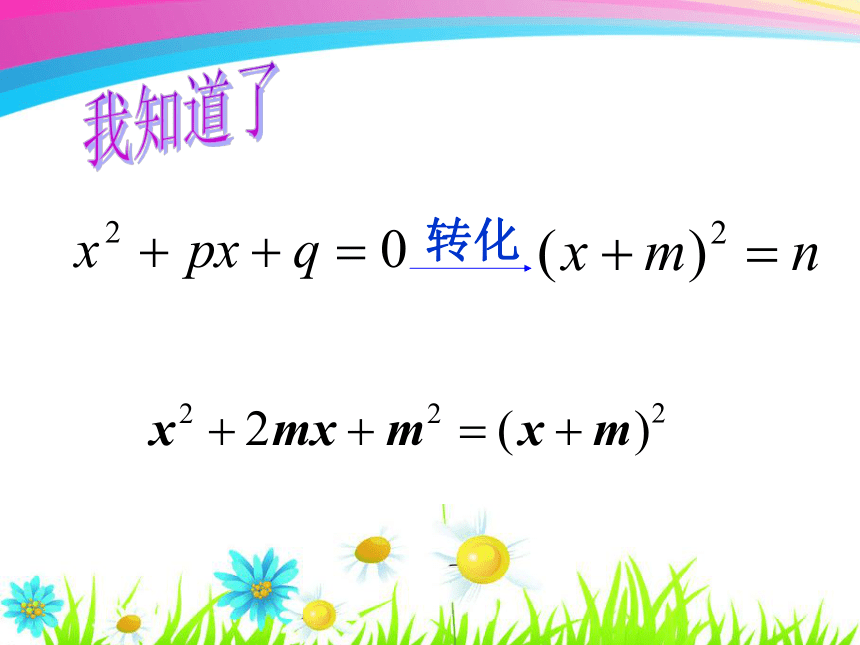



文档简介
(共19张PPT)
2 用配方法解一元二次方程(2)
五四制鲁教版八年级下册
x2-6x+9=4
x2-6x=-5
x2-6x+5=0
(x-3)2=4
探究
我知道了
转化
x2+12x+______=(x+6)2
x2+7x+______=(x+ )2
x2- x+______=(x- )2
x2-20x+______=(x- )2
思考:
常数项和一次项系数有什么关系?
我能行
62
102
10
填一填
1
4
总结:配方主要是加上
一次项系数的一半的平方
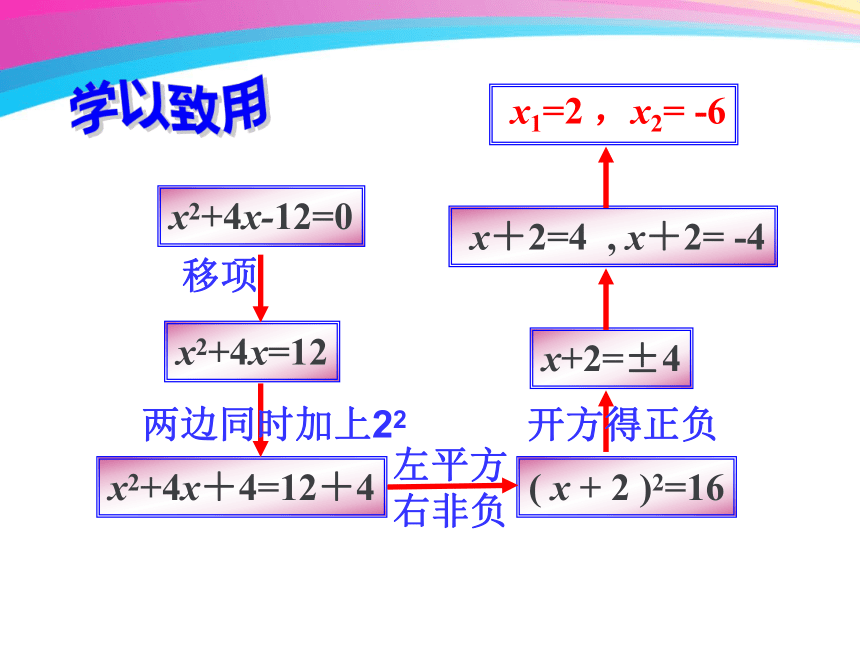
x2+4x-12=0
x2+4x=12
x2+4x+4=12+4
( x + 2 )2=16
x+2=±4
x+2=4 , x+2= -4
x1=2 ,x2= -6
学以致用
移项
两边同时加上22
左平方右非负
开方得正负
学以致用
x1,x2都是原问题的解吗?
x1=2 ,x2= -6
通过配成完全平方形式来解一元二次方程的方法,叫做配方法。
对二次项系数是1的一元二次方程,配方时要注意在方程两边同时加上一次项系数一半的平方。
我知道了
例2:用配方法解方程
解:
配方,得
开平方,得
移项,得
∴原方程的解为
心动 不如行动
解: x2+12x=15 ①
x2+12x+6=15+6 ②
(x+6)2=21 ③
x+6= ④
⑤
火眼金睛
1. x2+12x-15=0
找出下列解答过程中的错误
2. x2+12x-15=0
解: x2+12x=15 ①
x2+12x+62=15 ②
(x+6)2=15 ③
x+6= ④
⑤
火眼金睛
火眼金睛
解: ①
②
③
④
⑤
3.
火眼金睛
解: ①
②
③
④
⑤
4.
(1)
(2)
(3)
(4)
练一练
选做:
1.移项:常数项右移;
2.配方:方程两边同时加上一次项系数一半的平方;
3.变形: (x+m)2=n(n≥0)
4.开方:得正负
5.解一元一次方程:
6.写出原方程的解.
畅谈收获
当堂检测
1.一元二次方程x2-6x-5=0配方可变形为A.(x-3)2=14 B. (x-3)2=4
C.(x+3)2=14 D. (x+3)2=4
2.若x2-4x+5= (x-2)2+m,则m= .
3.解方程: x2-2x=4
选做1.已知等腰三角形的一边长为9,另一边长为方程x2-8x+15=0的根,则该等腰三角形的周长为 .
2.已知方程x2+4x+n=0可以配方成(x+m)2=3,则 (m-n)2016= .
A
1
19或21或23
1
作业:
必做:
课本P58 习题8.4
知识技能1
能力挑战一:
求
已知
如图,在一块长35m,宽26m矩形地面上,修建同样宽的两条互相垂直的道路,剩余部分栽种花草,在使剩余部分的面积为850m2,道路的宽应是多少?
解:设道路的宽为 x m,根据题意,得
(35-x) (26-x) =850.
化简:x2 - 61x+60 =0
35m
26m
解这个方程,得
x1 =1 x2 =60
答:道路的宽应为1m.
(不合题意,舍去)
能力挑战二:
2 用配方法解一元二次方程(2)
五四制鲁教版八年级下册
x2-6x+9=4
x2-6x=-5
x2-6x+5=0
(x-3)2=4
探究
我知道了
转化
x2+12x+______=(x+6)2
x2+7x+______=(x+ )2
x2- x+______=(x- )2
x2-20x+______=(x- )2
思考:
常数项和一次项系数有什么关系?
我能行
62
102
10
填一填
1
4
总结:配方主要是加上
一次项系数的一半的平方
x2+4x-12=0
x2+4x=12
x2+4x+4=12+4
( x + 2 )2=16
x+2=±4
x+2=4 , x+2= -4
x1=2 ,x2= -6
学以致用
移项
两边同时加上22
左平方右非负
开方得正负
学以致用
x1,x2都是原问题的解吗?
x1=2 ,x2= -6
通过配成完全平方形式来解一元二次方程的方法,叫做配方法。
对二次项系数是1的一元二次方程,配方时要注意在方程两边同时加上一次项系数一半的平方。
我知道了
例2:用配方法解方程
解:
配方,得
开平方,得
移项,得
∴原方程的解为
心动 不如行动
解: x2+12x=15 ①
x2+12x+6=15+6 ②
(x+6)2=21 ③
x+6= ④
⑤
火眼金睛
1. x2+12x-15=0
找出下列解答过程中的错误
2. x2+12x-15=0
解: x2+12x=15 ①
x2+12x+62=15 ②
(x+6)2=15 ③
x+6= ④
⑤
火眼金睛
火眼金睛
解: ①
②
③
④
⑤
3.
火眼金睛
解: ①
②
③
④
⑤
4.
(1)
(2)
(3)
(4)
练一练
选做:
1.移项:常数项右移;
2.配方:方程两边同时加上一次项系数一半的平方;
3.变形: (x+m)2=n(n≥0)
4.开方:得正负
5.解一元一次方程:
6.写出原方程的解.
畅谈收获
当堂检测
1.一元二次方程x2-6x-5=0配方可变形为A.(x-3)2=14 B. (x-3)2=4
C.(x+3)2=14 D. (x+3)2=4
2.若x2-4x+5= (x-2)2+m,则m= .
3.解方程: x2-2x=4
选做1.已知等腰三角形的一边长为9,另一边长为方程x2-8x+15=0的根,则该等腰三角形的周长为 .
2.已知方程x2+4x+n=0可以配方成(x+m)2=3,则 (m-n)2016= .
A
1
19或21或23
1
作业:
必做:
课本P58 习题8.4
知识技能1
能力挑战一:
求
已知
如图,在一块长35m,宽26m矩形地面上,修建同样宽的两条互相垂直的道路,剩余部分栽种花草,在使剩余部分的面积为850m2,道路的宽应是多少?
解:设道路的宽为 x m,根据题意,得
(35-x) (26-x) =850.
化简:x2 - 61x+60 =0
35m
26m
解这个方程,得
x1 =1 x2 =60
答:道路的宽应为1m.
(不合题意,舍去)
能力挑战二:
