4.2 平行线分线段成比例 课件(共27张PPT)
文档属性
| 名称 | 4.2 平行线分线段成比例 课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 746.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 00:00:00 | ||
图片预览

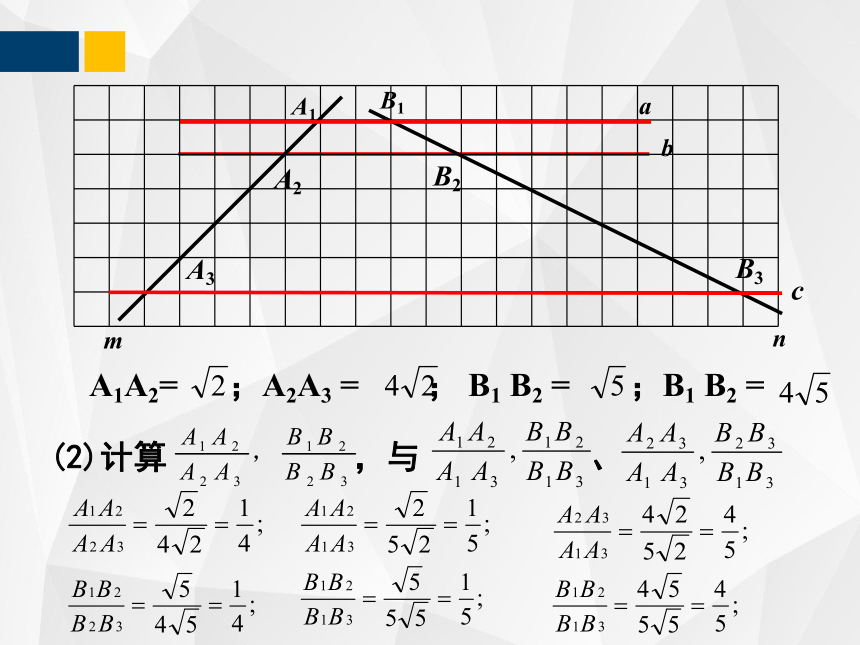

文档简介
(共27张PPT)
北师大版九年级上册
第四章
图形的相似
4.2 平行线分线段成比例
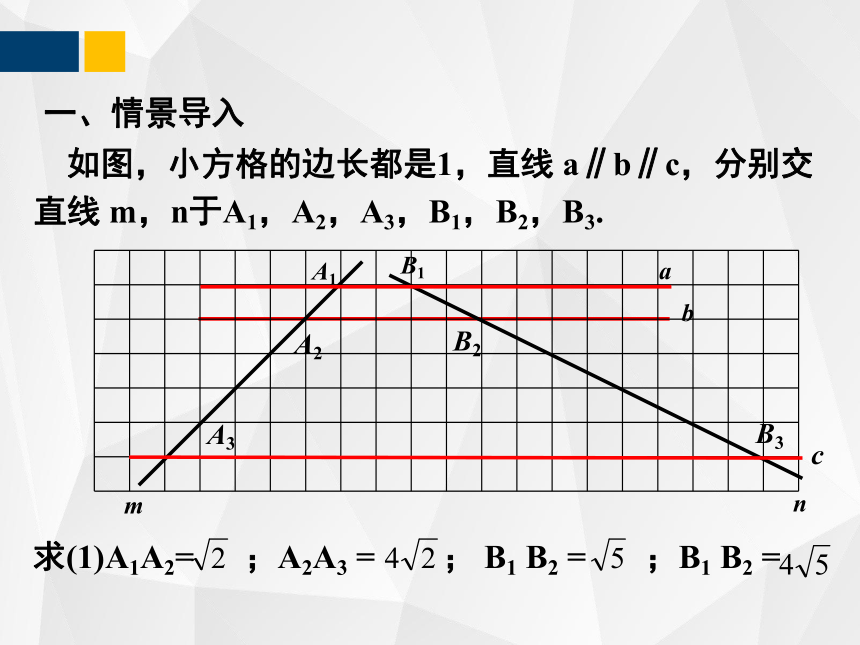
如图,小方格的边长都是1,直线 a∥b∥c,分别交直线 m,n于A1,A2,A3,B1,B2,B3.
A2
A3
A1
B1
B2
B3
b
m
n
a
c
一、情景导入
求(1)A1A2= ;A2A3 = ; B1 B2 = ;B1 B2 =
A2
A3
A1
B1
B2
B3
b
m
n
a
c
(2)计算 ,与 、
A1A2= ;A2A3 = ; B1 B2 = ;B1 B2 =
A2
A3
A1
B1
B2
B3
b
m
n
a
c
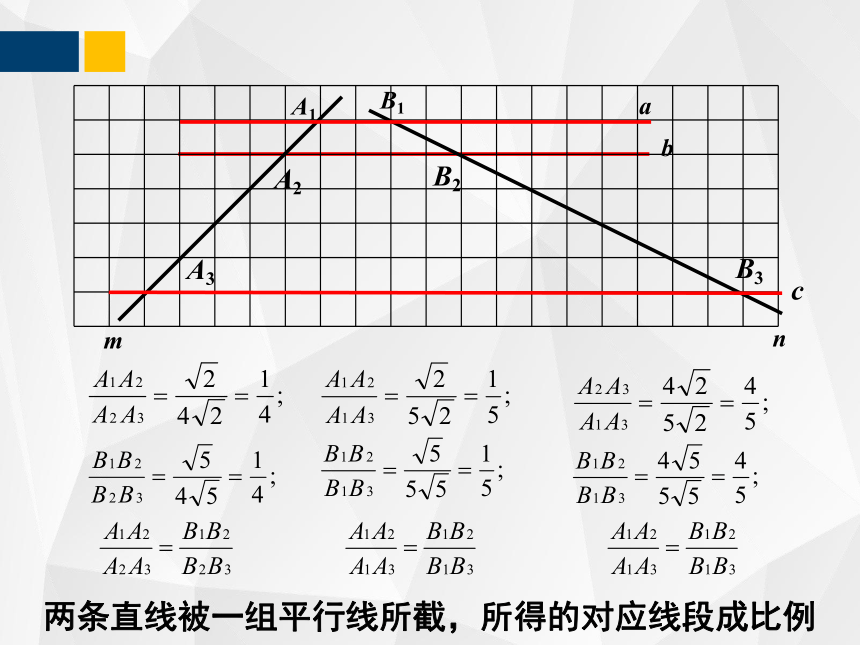
两条直线被一组平行线所截,所得的对应线段成比例
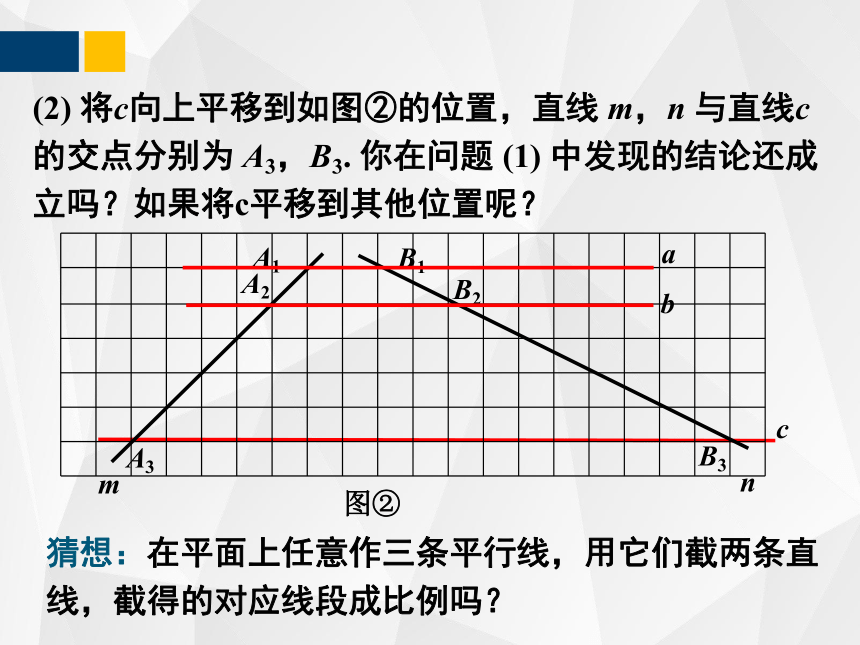
(2) 将c向上平移到如图②的位置,直线 m,n 与直线c的交点分别为 A3,B3. 你在问题 (1) 中发现的结论还成立吗?如果将c平移到其他位置呢?
A3
A2
A1
B1
B3
B2
c
m
n
a
b
图②
猜想:在平面上任意作三条平行线,用它们截两条直线,截得的对应线段成比例吗?
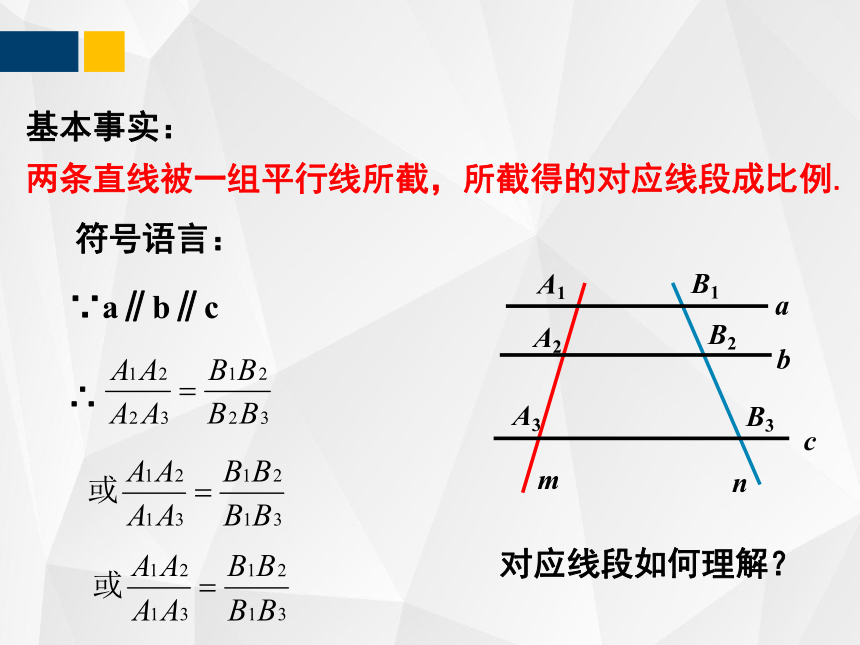
基本事实:
两条直线被一组平行线所截,所截得的对应线段成比例.
符号语言:
∵a∥b∥c
A1
A2
A3
B1
B2
B3
b
c
m
n
a
∴
对应线段如何理解?
如图,直线a∥b∥ c,由平行线分线段成比例的基本事实,我们可以得出图中对应成比例的线段,
A1
A2
A3
B1
B2
B3
b
c
m
n
a
思考:把直线 n 向左或向右任意平移,这些线段是否依然成比例呢?
活动探究
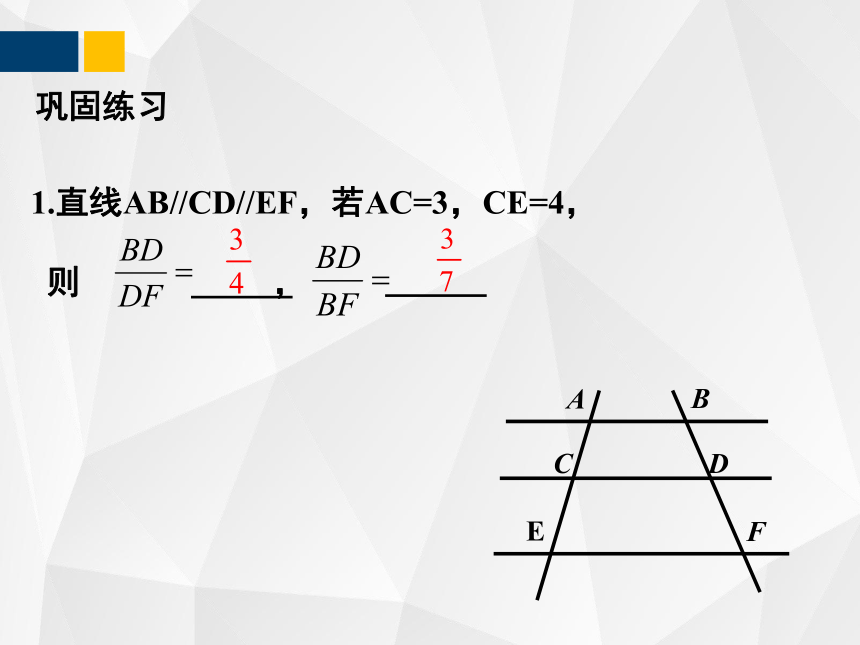
1.直线AB//CD//EF,若AC=3,CE=4,
则 ,
巩固练习
A
C
E
B
D
F
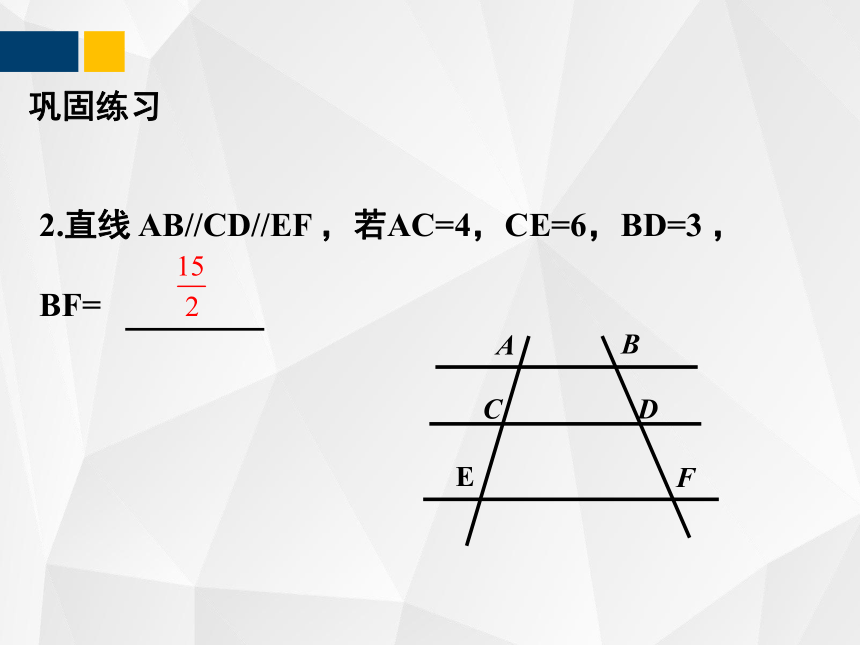
2.直线 AB//CD//EF ,若AC=4,CE=6,BD=3 ,BF=
巩固练习
A
C
E
B
D
F
A1
A2
A3
b
c
m
B1
B2
B3
n
a
在新的图形中,上面的线段是否仍然成比例?
A1(B1)
A2
A3
B2
B3
( )
“A”字型基本图形
直线 n 向左平移到 B1 与A1 重合的位置,图中有哪些成比例线段?
成立,平移时对应线段的长度不会改变
B1
B2
B3
n
A1
A2
A3
b
c
m
B1
B2
B3
n
a
直线 n 向左平移到 B2 与A2 重合的位置,图中有哪些成比例线段?
在新的图形中,上面的线段是否仍然成比例?
A2(B2)
A1
A3
B1
B3
( )
“X”字型基本图形
成立,平移时对应线段的长度不会改变
B1
B2
B3
n
平行线分线段成比例的推论:
平行于三角形一边的直线与其他两边(或其延长线)相交,截得的对应线段成比例.
例:如图,在△ABC中,E,F分别是AB和AC上的点,且EF∥BC.
(1)如果AE=7,EB=5,FC=4,那么AF的长是多少?
(2)如果AB=10,AE=6,AF=5,那么FC的长是多少?
A
B
C
E
F
解:(1)
∵ EF∥BC,
AE AF
EB FC
∴
——
——,
=
7 AF
5 4
——
——,
=
即
=
28
5
——.
∴
AF
三、典例讲解
例:如图,在△ABC中,E,F分别是AB和AC上的点,且EF∥BC.
(1)如果AE=7,EB=5,FC=4,那么AF的长是多少?
(2)如果AB=10,AE=6,AF=5,那么FC的长是多少?
A
B
C
E
F
解:(2)
AE AF
AB AC
∴
——
——,
=
6 5
10 AC
——
——.
=
即
=
25
3
——,
∴
AC
=
10
3
—.
∴
FC
三、典例讲解
2.如图,EG∥BC,GF∥DC,AE=3,EB=2,AF=6, 求AD的值.
解: ∵EG∥BC
∴ = =
又∵GF∥DC
∴ =
∴ =
∴FD= AF= ×6=4
∴AD=AF+FD=6+4=10
三、典例讲解
1.如图,已知l1∥l2∥l3,下列比例式错误的是( )
AC BD
CE DF
A.
——
——
=
CE DF
AE BF
C.
——
——
=
AC BD
AE BF
B.
——
——
=
AE BD
BF AC
D.
——
——
=
D
A
B
C
D
E
F
l1
l2
l3
四、课堂练习
2.如图,已知l1∥l2∥l3,下列比例式成立的是( )
AD CE
DF BC
A.
——
——
=
AF BE
DF CE
C.
——
——
=
AD BC
BE AF
B.
——
——
=
CE AD
DF BC
D.
——
——
=
C
A
B
C
D
E
F
l1
l2
l3
四、课堂练习
四、课堂练习
A
B
C
D
E
F
l1
l2
l3
3.如图,l1∥l2∥l3,其中AC=2,BD=3,CE=4,
则DF=________.
6
4.如图,BC∥DE,AB=15,AC=9,BD = 10,则
AE=______.
15
A
D
E
B
C
四、课堂练习
5.如图,DE∥BC,AB=6,AC=9,AD=2,则
EC=______.
12
A
B
C
E
D
四、课堂练习
6.如图,直线a∥b∥c,直线l1、l2与这三条平行线分别交于点A,B,C和点D,E,F.若AB∶BC=1∶2,
EF=6,则DE的长为________.
3
四、课堂练习
7.如图,在△ABC中,D,E,F分别是AB,AC,BC上的点,且 DE∥BC,EF∥AB,AD∶DB=2∶3,BC=20 cm,求BF的长
四、课堂练习
解:∵DE∥BC,EF∥AB,
∴四边形BDEF是平行四边形,∴BF=DE,
∵AD∶DB=2∶3,
∴AD∶AB=2∶5. ∵DE∥BC,
∴DE∶BC=AD∶AB=2∶5,
即DE∶20=2∶5,
∴DE=8,∴BF=8.
故BF的长为8 cm.
四、课堂练习
8.如图,在△ABC中,D是AB上的一点,过点D作DE∥BC交边AC于点E,过点E作EF∥DC交边AD于点F,AD=2 cm,AB=8 cm,求 及 的值.
解:∵DE∥BC
∴
又∵EF∥DC
∴
∴
平行线分线
段成比例
平行于三角形一边的直线与其他两边
相交,截得的对应线段成比例.
基本事实
推论
两条直线被一组平行线所截,所得
的对应线段成比例.
一、平行线分线段成比例定理:
二、要熟悉该定理的几种基本图形:
A
B
C
E
D
A
B
C
D
E
“A”字型基本图形
“X”字型基本图形
五、课堂小结
六、布置作业
课本P84 习题4.3 第1,2,3,4题
谢谢聆听
北师大版九年级上册
第四章
图形的相似
4.2 平行线分线段成比例
如图,小方格的边长都是1,直线 a∥b∥c,分别交直线 m,n于A1,A2,A3,B1,B2,B3.
A2
A3
A1
B1
B2
B3
b
m
n
a
c
一、情景导入
求(1)A1A2= ;A2A3 = ; B1 B2 = ;B1 B2 =
A2
A3
A1
B1
B2
B3
b
m
n
a
c
(2)计算 ,与 、
A1A2= ;A2A3 = ; B1 B2 = ;B1 B2 =
A2
A3
A1
B1
B2
B3
b
m
n
a
c
两条直线被一组平行线所截,所得的对应线段成比例
(2) 将c向上平移到如图②的位置,直线 m,n 与直线c的交点分别为 A3,B3. 你在问题 (1) 中发现的结论还成立吗?如果将c平移到其他位置呢?
A3
A2
A1
B1
B3
B2
c
m
n
a
b
图②
猜想:在平面上任意作三条平行线,用它们截两条直线,截得的对应线段成比例吗?
基本事实:
两条直线被一组平行线所截,所截得的对应线段成比例.
符号语言:
∵a∥b∥c
A1
A2
A3
B1
B2
B3
b
c
m
n
a
∴
对应线段如何理解?
如图,直线a∥b∥ c,由平行线分线段成比例的基本事实,我们可以得出图中对应成比例的线段,
A1
A2
A3
B1
B2
B3
b
c
m
n
a
思考:把直线 n 向左或向右任意平移,这些线段是否依然成比例呢?
活动探究
1.直线AB//CD//EF,若AC=3,CE=4,
则 ,
巩固练习
A
C
E
B
D
F
2.直线 AB//CD//EF ,若AC=4,CE=6,BD=3 ,BF=
巩固练习
A
C
E
B
D
F
A1
A2
A3
b
c
m
B1
B2
B3
n
a
在新的图形中,上面的线段是否仍然成比例?
A1(B1)
A2
A3
B2
B3
( )
“A”字型基本图形
直线 n 向左平移到 B1 与A1 重合的位置,图中有哪些成比例线段?
成立,平移时对应线段的长度不会改变
B1
B2
B3
n
A1
A2
A3
b
c
m
B1
B2
B3
n
a
直线 n 向左平移到 B2 与A2 重合的位置,图中有哪些成比例线段?
在新的图形中,上面的线段是否仍然成比例?
A2(B2)
A1
A3
B1
B3
( )
“X”字型基本图形
成立,平移时对应线段的长度不会改变
B1
B2
B3
n
平行线分线段成比例的推论:
平行于三角形一边的直线与其他两边(或其延长线)相交,截得的对应线段成比例.
例:如图,在△ABC中,E,F分别是AB和AC上的点,且EF∥BC.
(1)如果AE=7,EB=5,FC=4,那么AF的长是多少?
(2)如果AB=10,AE=6,AF=5,那么FC的长是多少?
A
B
C
E
F
解:(1)
∵ EF∥BC,
AE AF
EB FC
∴
——
——,
=
7 AF
5 4
——
——,
=
即
=
28
5
——.
∴
AF
三、典例讲解
例:如图,在△ABC中,E,F分别是AB和AC上的点,且EF∥BC.
(1)如果AE=7,EB=5,FC=4,那么AF的长是多少?
(2)如果AB=10,AE=6,AF=5,那么FC的长是多少?
A
B
C
E
F
解:(2)
AE AF
AB AC
∴
——
——,
=
6 5
10 AC
——
——.
=
即
=
25
3
——,
∴
AC
=
10
3
—.
∴
FC
三、典例讲解
2.如图,EG∥BC,GF∥DC,AE=3,EB=2,AF=6, 求AD的值.
解: ∵EG∥BC
∴ = =
又∵GF∥DC
∴ =
∴ =
∴FD= AF= ×6=4
∴AD=AF+FD=6+4=10
三、典例讲解
1.如图,已知l1∥l2∥l3,下列比例式错误的是( )
AC BD
CE DF
A.
——
——
=
CE DF
AE BF
C.
——
——
=
AC BD
AE BF
B.
——
——
=
AE BD
BF AC
D.
——
——
=
D
A
B
C
D
E
F
l1
l2
l3
四、课堂练习
2.如图,已知l1∥l2∥l3,下列比例式成立的是( )
AD CE
DF BC
A.
——
——
=
AF BE
DF CE
C.
——
——
=
AD BC
BE AF
B.
——
——
=
CE AD
DF BC
D.
——
——
=
C
A
B
C
D
E
F
l1
l2
l3
四、课堂练习
四、课堂练习
A
B
C
D
E
F
l1
l2
l3
3.如图,l1∥l2∥l3,其中AC=2,BD=3,CE=4,
则DF=________.
6
4.如图,BC∥DE,AB=15,AC=9,BD = 10,则
AE=______.
15
A
D
E
B
C
四、课堂练习
5.如图,DE∥BC,AB=6,AC=9,AD=2,则
EC=______.
12
A
B
C
E
D
四、课堂练习
6.如图,直线a∥b∥c,直线l1、l2与这三条平行线分别交于点A,B,C和点D,E,F.若AB∶BC=1∶2,
EF=6,则DE的长为________.
3
四、课堂练习
7.如图,在△ABC中,D,E,F分别是AB,AC,BC上的点,且 DE∥BC,EF∥AB,AD∶DB=2∶3,BC=20 cm,求BF的长
四、课堂练习
解:∵DE∥BC,EF∥AB,
∴四边形BDEF是平行四边形,∴BF=DE,
∵AD∶DB=2∶3,
∴AD∶AB=2∶5. ∵DE∥BC,
∴DE∶BC=AD∶AB=2∶5,
即DE∶20=2∶5,
∴DE=8,∴BF=8.
故BF的长为8 cm.
四、课堂练习
8.如图,在△ABC中,D是AB上的一点,过点D作DE∥BC交边AC于点E,过点E作EF∥DC交边AD于点F,AD=2 cm,AB=8 cm,求 及 的值.
解:∵DE∥BC
∴
又∵EF∥DC
∴
∴
平行线分线
段成比例
平行于三角形一边的直线与其他两边
相交,截得的对应线段成比例.
基本事实
推论
两条直线被一组平行线所截,所得
的对应线段成比例.
一、平行线分线段成比例定理:
二、要熟悉该定理的几种基本图形:
A
B
C
E
D
A
B
C
D
E
“A”字型基本图形
“X”字型基本图形
五、课堂小结
六、布置作业
课本P84 习题4.3 第1,2,3,4题
谢谢聆听
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
