圆锥的体积(例2)(课件) 六年级下册数学人教版(共51张PPT)
文档属性
| 名称 | 圆锥的体积(例2)(课件) 六年级下册数学人教版(共51张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 16:26:44 | ||
图片预览



文档简介
(共51张PPT)
圆锥的体积
(例2)
RJ·六年级下册
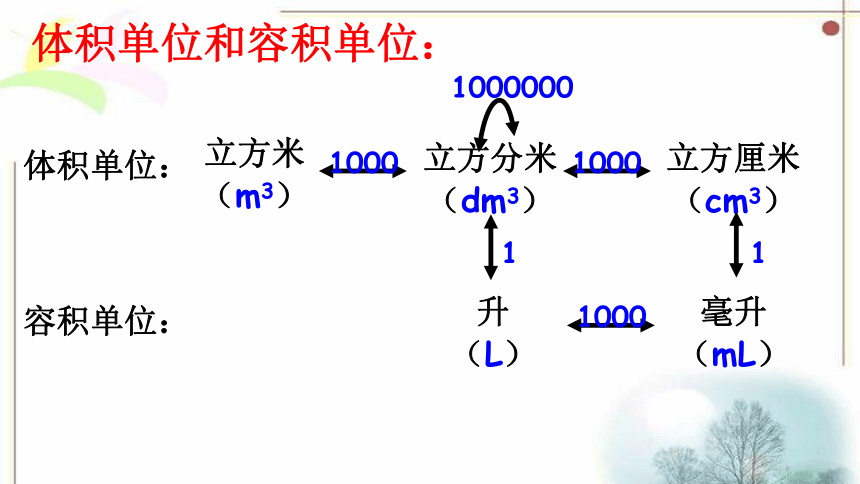
体积单位和容积单位:
立方米
(m3)
立方分米
(dm3)
立方厘米
(cm3)
升
(L)
1000
1000
1
毫升
(mL)
1000
体积单位:
容积单位:
1
1000000
上节课,我们认识了圆锥,你们知道圆锥有哪些特征吗?
复习导入
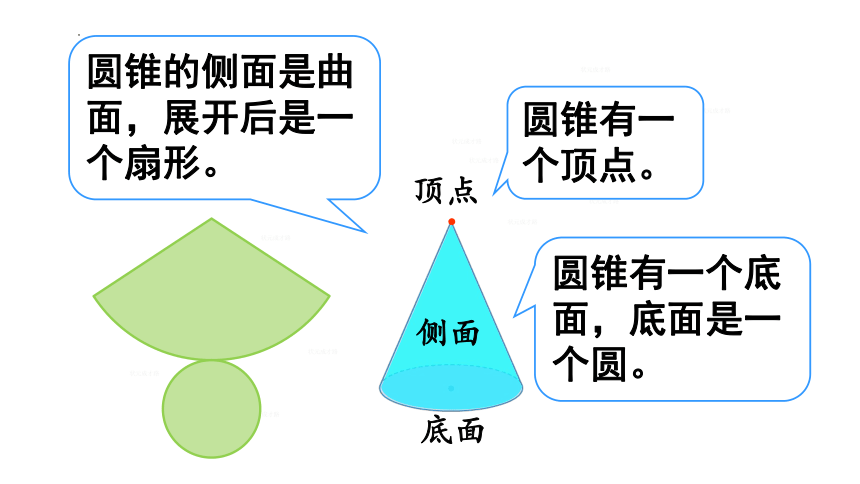
顶点
底面
圆锥有一个顶点。
圆锥有一个底面,底面是一个圆。
侧面
圆锥的侧面是曲面,展开后是一个扇形。
高
顶点到底面的距离是圆锥的高。
圆锥只有一条高。
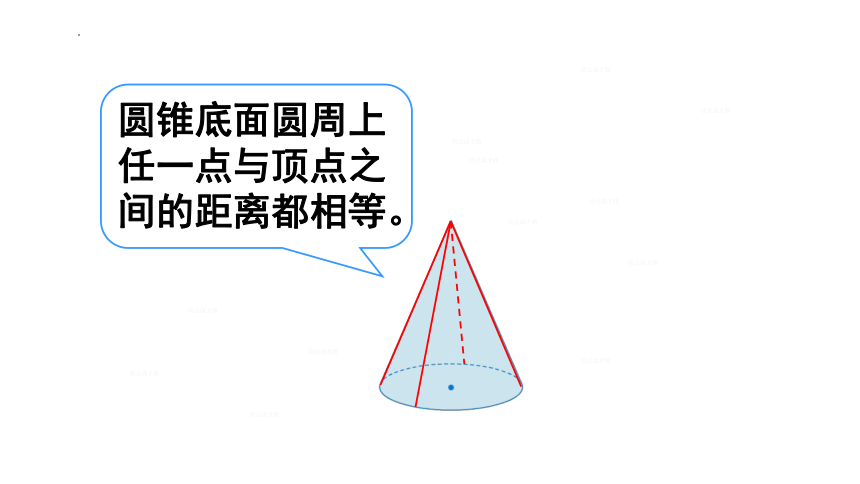
圆锥底面圆周上任一点与顶点之间的距离都相等。
今天,我们来学习圆锥的体积。
探索新知
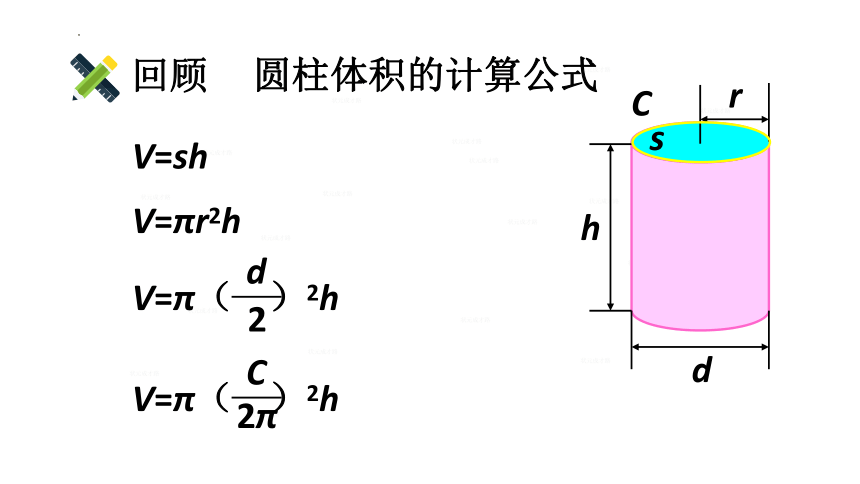
回顾
圆柱体积的计算公式
V=sh
h
d
s
V=πr2h
r
V=π( )2h
2
d
V=π( )2h
2π
C
C
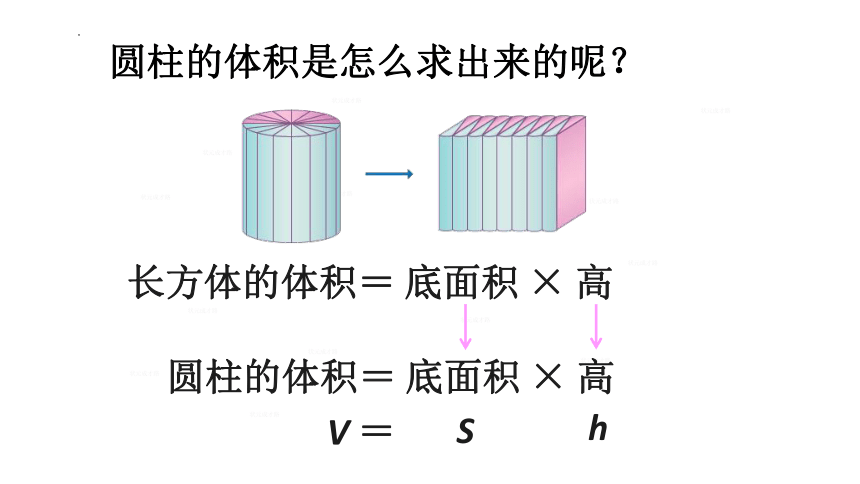
圆柱的体积= 底面积 × 高
长方体的体积= 底面积 × 高
V =
S
h
圆柱的体积是怎么求出来的呢?
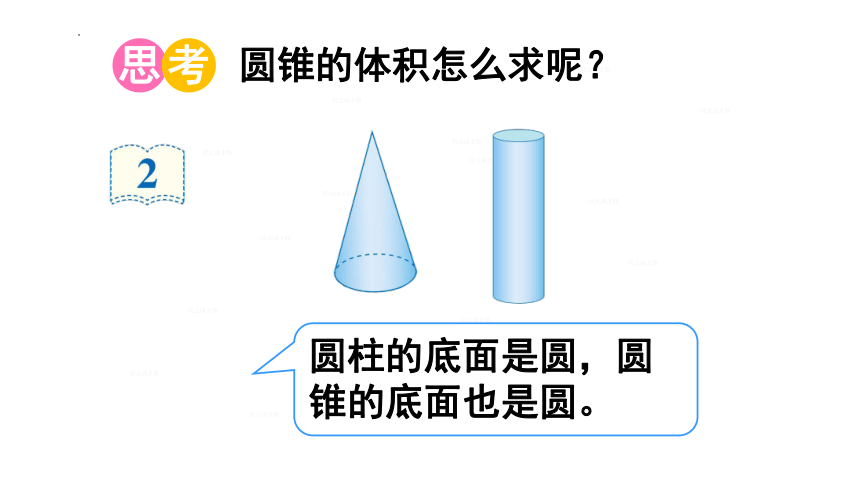
圆柱的底面是圆,圆锥的底面也是圆。
思
考
圆锥的体积怎么求呢?
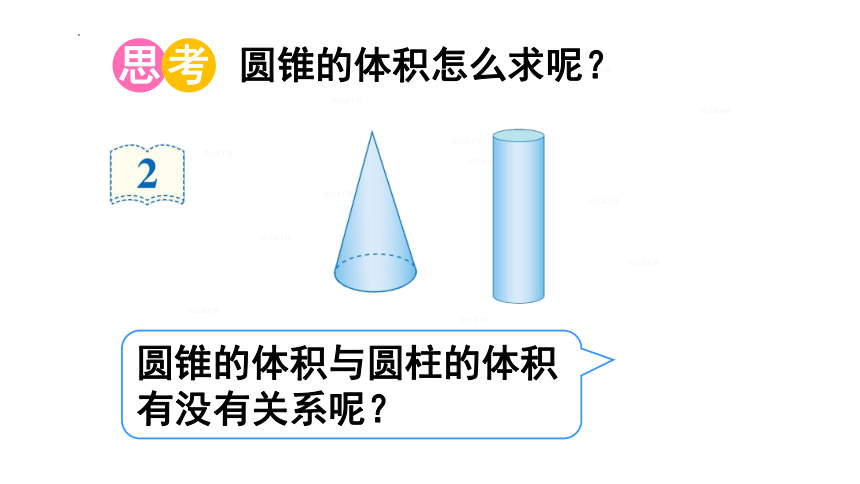
圆锥的体积与圆柱的体积有没有关系呢?
思
考
圆锥的体积怎么求呢?
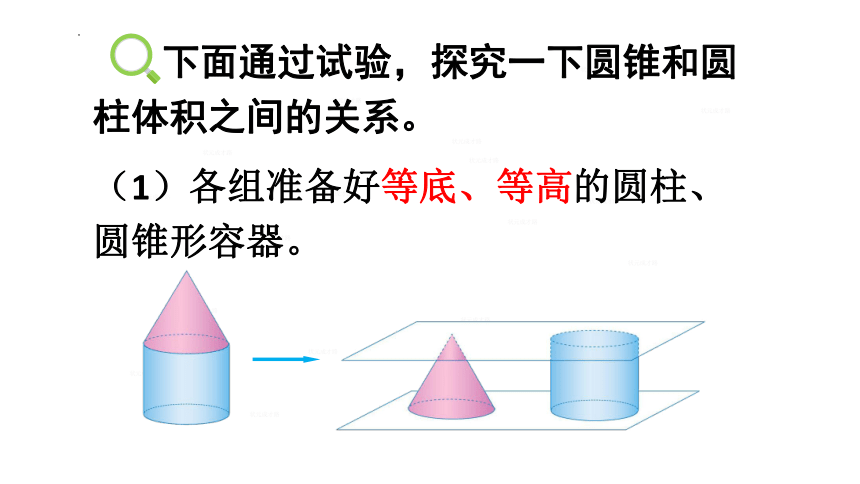
下面通过试验,探究一下圆锥和圆柱体积之间的关系。
(1)各组准备好等底、等高的圆柱、圆锥形容器。
(2)用倒沙子或水的方法试一试。
三次正好装满。
我把圆柱装满水,再往圆锥里倒。
正好倒了三次。
等高
等底
(3)通过实验,你发现圆锥的体积与同它等底、等高的圆柱的体积之间的关系了吗?
V圆锥= V圆柱= Sh
h
s
r
d
C
圆锥已知底面积、体积,求高:
体积×3÷底面积=高
h
s
圆锥已知高、体积,求底面积:
体积×3÷高=底面积
圆锥已知底面积、高,求体积:
底面积×高÷3=体积
1. 一个圆锥形的零件,底面积是19cm2,高是12cm,这个零件的体积是多少?
答:这个零件的体积是76cm 。
×19 ×12=76(cm )
做一做
圆柱体积(cm3) 3 9
圆锥体积(cm3) 15
2.
1
45
3
3. 一个圆锥形的底面周长是31.4cm,高是12cm,这个零件的体积是多少?
4. 一个圆锥形的体积是314cm3,高是12cm,这个零件的底面积是多少?
314×3=942( cm )
942÷12=78.5(cm2)
答:这个零件的底面积是78.5平方厘米。
5. 一个圆锥形的体积是314cm3,底面积是78.5cm2,这个零件的高是多少?
314×3=942( cm )
942÷78.5=12(cm)
答:这个零件的底面积是12厘米。
已知一个圆柱体和一个圆锥体的底面积相等, 高也相等,圆柱的体积和圆锥体积的关系是:
A. 圆柱的体积是圆锥体积的 。
B. 圆锥的体积是圆柱体积的 。
C. 圆柱的体积比圆锥体积多 。
D. 圆锥的体积比圆柱体积少 。
E. 圆柱与圆锥体积之比是 。
F. 圆锥与圆柱体积之比是 。
3倍
1:3
3:1
2倍
总结
一个圆柱和一个圆锥的体积相等,它们不可能( )。
A、等底不等高 B、等高不等底
C、等底等高 D、不等底不等高
×
√
×
随堂演练
√
5、圆柱的体积是圆锥体积的3倍。 ( )
6、圆锥的底面积越大,体积就越大。 ( )
7、圆锥的高越大,体积就越大。 ( )
8、圆锥的体积与底面积和高都有关系。 ( )
9、等底等高的圆柱和圆锥的体积比是3:1。 ( )
10、等底等高的圆锥和圆柱的体积比是1:3. ( )
√
×
√
√
×
×
1.等底等高的圆柱和圆锥,圆柱的体积是12立方分米,圆锥的体积是( )立方分米。
2.用15个同样的圆锥铝坯,可以铸造成( )个与它等底等高的圆柱体铝坯。
4
5
3.一个圆锥的高不变,底面半径扩大到原来的2倍,它的体积就扩大到原来的( )倍。
4
填空
思 考:
1、一个圆锥与一个圆柱等底等高,
已知圆锥的体积是 8 立方米,
圆柱的体积是( )。
2、一个圆锥与一个圆柱等底等体积,
已知圆柱的高是 2 厘米, 圆锥的
高是( )。
3、一个圆锥与一个圆柱等高等体积,
已知圆柱的底面积是 6平方米,
圆锥的底面积是( )。
24立方米
6 厘米
18平方米
1、在一个圆柱体内削一个最大的圆锥,他们的体积比是( ):( )
2、将一个圆柱体铝块熔铸成圆锥体,他们的体积比是( ):( )
区别:“熔”与“削”
V= sh
h
s
V= πr2h
r
V= π( )2h
2
d
d
C
V= π( )2h
2π
C
课堂小结
圆锥的体积
(例2)
RJ·六年级下册
体积单位和容积单位:
立方米
(m3)
立方分米
(dm3)
立方厘米
(cm3)
升
(L)
1000
1000
1
毫升
(mL)
1000
体积单位:
容积单位:
1
1000000
上节课,我们认识了圆锥,你们知道圆锥有哪些特征吗?
复习导入
顶点
底面
圆锥有一个顶点。
圆锥有一个底面,底面是一个圆。
侧面
圆锥的侧面是曲面,展开后是一个扇形。
高
顶点到底面的距离是圆锥的高。
圆锥只有一条高。
圆锥底面圆周上任一点与顶点之间的距离都相等。
今天,我们来学习圆锥的体积。
探索新知
回顾
圆柱体积的计算公式
V=sh
h
d
s
V=πr2h
r
V=π( )2h
2
d
V=π( )2h
2π
C
C
圆柱的体积= 底面积 × 高
长方体的体积= 底面积 × 高
V =
S
h
圆柱的体积是怎么求出来的呢?
圆柱的底面是圆,圆锥的底面也是圆。
思
考
圆锥的体积怎么求呢?
圆锥的体积与圆柱的体积有没有关系呢?
思
考
圆锥的体积怎么求呢?
下面通过试验,探究一下圆锥和圆柱体积之间的关系。
(1)各组准备好等底、等高的圆柱、圆锥形容器。
(2)用倒沙子或水的方法试一试。
三次正好装满。
我把圆柱装满水,再往圆锥里倒。
正好倒了三次。
等高
等底
(3)通过实验,你发现圆锥的体积与同它等底、等高的圆柱的体积之间的关系了吗?
V圆锥= V圆柱= Sh
h
s
r
d
C
圆锥已知底面积、体积,求高:
体积×3÷底面积=高
h
s
圆锥已知高、体积,求底面积:
体积×3÷高=底面积
圆锥已知底面积、高,求体积:
底面积×高÷3=体积
1. 一个圆锥形的零件,底面积是19cm2,高是12cm,这个零件的体积是多少?
答:这个零件的体积是76cm 。
×19 ×12=76(cm )
做一做
圆柱体积(cm3) 3 9
圆锥体积(cm3) 15
2.
1
45
3
3. 一个圆锥形的底面周长是31.4cm,高是12cm,这个零件的体积是多少?
4. 一个圆锥形的体积是314cm3,高是12cm,这个零件的底面积是多少?
314×3=942( cm )
942÷12=78.5(cm2)
答:这个零件的底面积是78.5平方厘米。
5. 一个圆锥形的体积是314cm3,底面积是78.5cm2,这个零件的高是多少?
314×3=942( cm )
942÷78.5=12(cm)
答:这个零件的底面积是12厘米。
已知一个圆柱体和一个圆锥体的底面积相等, 高也相等,圆柱的体积和圆锥体积的关系是:
A. 圆柱的体积是圆锥体积的 。
B. 圆锥的体积是圆柱体积的 。
C. 圆柱的体积比圆锥体积多 。
D. 圆锥的体积比圆柱体积少 。
E. 圆柱与圆锥体积之比是 。
F. 圆锥与圆柱体积之比是 。
3倍
1:3
3:1
2倍
总结
一个圆柱和一个圆锥的体积相等,它们不可能( )。
A、等底不等高 B、等高不等底
C、等底等高 D、不等底不等高
×
√
×
随堂演练
√
5、圆柱的体积是圆锥体积的3倍。 ( )
6、圆锥的底面积越大,体积就越大。 ( )
7、圆锥的高越大,体积就越大。 ( )
8、圆锥的体积与底面积和高都有关系。 ( )
9、等底等高的圆柱和圆锥的体积比是3:1。 ( )
10、等底等高的圆锥和圆柱的体积比是1:3. ( )
√
×
√
√
×
×
1.等底等高的圆柱和圆锥,圆柱的体积是12立方分米,圆锥的体积是( )立方分米。
2.用15个同样的圆锥铝坯,可以铸造成( )个与它等底等高的圆柱体铝坯。
4
5
3.一个圆锥的高不变,底面半径扩大到原来的2倍,它的体积就扩大到原来的( )倍。
4
填空
思 考:
1、一个圆锥与一个圆柱等底等高,
已知圆锥的体积是 8 立方米,
圆柱的体积是( )。
2、一个圆锥与一个圆柱等底等体积,
已知圆柱的高是 2 厘米, 圆锥的
高是( )。
3、一个圆锥与一个圆柱等高等体积,
已知圆柱的底面积是 6平方米,
圆锥的底面积是( )。
24立方米
6 厘米
18平方米
1、在一个圆柱体内削一个最大的圆锥,他们的体积比是( ):( )
2、将一个圆柱体铝块熔铸成圆锥体,他们的体积比是( ):( )
区别:“熔”与“削”
V= sh
h
s
V= πr2h
r
V= π( )2h
2
d
d
C
V= π( )2h
2π
C
课堂小结
