13.1.2线段的垂直平分线的性质(1) 课件(22张ppt)
文档属性
| 名称 | 13.1.2线段的垂直平分线的性质(1) 课件(22张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 18:12:14 | ||
图片预览






文档简介
(共22张PPT)
13.1.2线段的垂直平分线的性质(1)
人教版八年级上册
教学目标
1、理解线段垂直平分线的性质和判定.能够证明线段垂直平分线的性质定理、判定定理及进行应用;能够利用尺规过直线外一点作该直线的垂线.
2、经历探索、猜测、证明的过程,进一步发展学生的推理证明意识和能力.
3、在数学活动中体会获得成功的体验,锻炼克服困难的意志,建立学习的自信心.
复习回顾
如果一个平面图形沿一条直线 .直线两旁的部分能够 ,这个图形就叫做轴对称图形.折痕所在的这条直线叫做_________.
对称轴
折叠
互相重合
忆一忆
把一个图形沿着某一条直线_______,如果它能够______________________,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做_______________.
折叠
与另一个图形重合
对称点
新知讲解
知识点1
线段垂直平分线的性质
探究
如图,直线 l 垂直平分线段 AB,P1,P2,P3,…是 l 上的点,分别量一量点 P1,P2,P3,… 到点 A 与点 B 的距离,你有什么发现?
A
B
l
P1
P2
P3
你能用不同的方法验证这一结论吗?
相等.
新知讲解
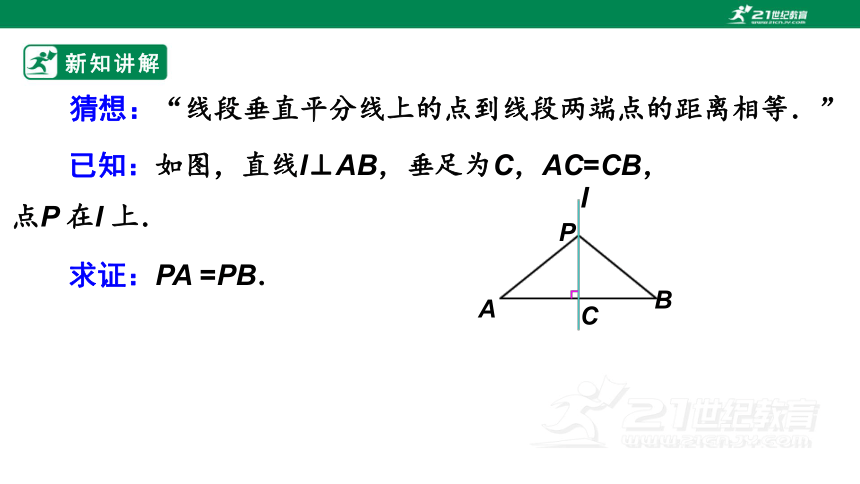
猜想:“线段垂直平分线上的点到线段两端点的距离相等.”
已知:如图,直线l⊥AB,垂足为C,AC=CB,点P 在l 上.
求证:PA =PB.
A
B
P
C
l
新知讲解
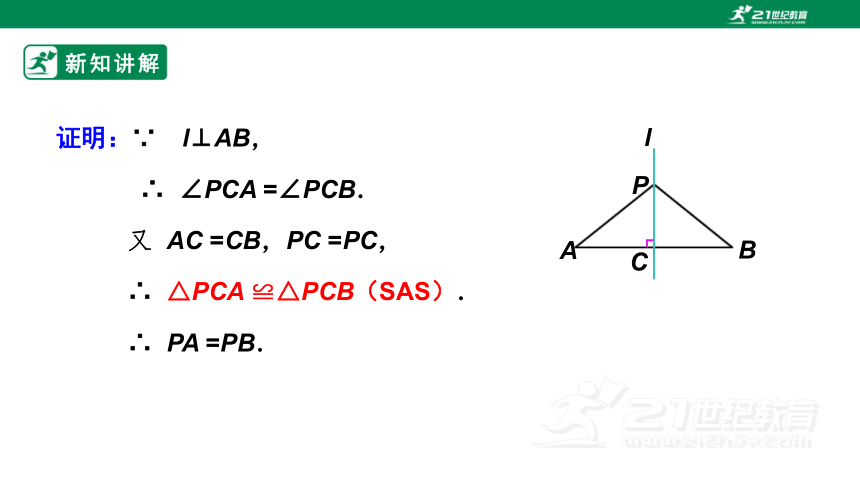
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
A
B
P
C
l
新知讲解
线段垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离相等.
用符号语言表示为:
∵ CA =CB,l⊥AB,∴ PA =PB.
A
B
P
C
l
巩固练习
1.如图,NM是线段AB的垂直平分线,下列说
法正确的有: .
①AB⊥MN,②AD=DB, ③MN⊥AB,
④MD=DN,⑤AB是MN的垂直平分线.
A
B
M
N
D
①②③
巩固练习
解:∵ AD⊥BC,BD =DC,
∴ AD 是BC 的垂直平分线,
∴ AB =AC.
2、如图,AD⊥BC,BD =DC,点C 在AE 的垂直平分线上,AB,AC,CE 的长度有什么关系?AB+BD与DE 有什么关系?
∴ AB =AC =CE.
∵ AB =CE,BD =DC,
∴ AB +BD =CD +CE.
即 AB +BD =DE .
∵ 点C 在AE 的垂直平分线上,
∴ AC =CE.
A
B
C
D
E
巩固练习
3.在△ABC中,∠ACB=90°,AB=8cm,BC的垂直平分线DE交AB于D点,则CD=_____ .
4cm
4.在△ABC,PM,QN分别垂直平分AB,AC,则:
(1)若BC=10cm则△APQ的周长=_____cm;
(2)若∠BAC=100°则∠PAQ=______.
10
20°
新知讲解
反过来,如果PA =PB,那么点P 是否在线段AB 的垂直平分线上呢?
点P 在线段AB 的垂直平分线上.
知识点2
线段垂直平分线的判定
新知讲解
已知:如图,在△ABP中,PA =PB.
求证:点P 在线段AB 的垂直平分线上.
P
A
B
C
证明:过点P 作线段AB 的垂线PC,垂足为C.
则∠PCA =∠PCB=90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,∴ 点P 在线段AB 的垂直平分线上.
新知讲解
用数学符号表示为:
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上.
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
P
A
B
C
典例讲解
例1、如图,已知在△ABC中,ON是AB的垂直平分线,并且OA=OC.
求证:点O在 BC的垂直平分线上.
A
B
C
O
N
∴点O在BC的垂直平分线上.(到一条线段的两个端点距离相等的点,在这条线段的垂直平分线上)
证明:连接OB.
∵ ON是AB的垂直平分线,(已知)
∴ OA=OB.(线段的垂直平分线上的点到这条线段的两个端点的距离相等)
∵ OA=OC,(已知)
∴ OB=OC.(等量代换)
巩固练习
A
B
M
N
D
4.下列说法正确的个数有( )
①若直线PE是线段AB的垂直平分线,则EA=EB,PA=PB;
②若PA=PB,EA=EB,则直线PE垂直平分线段AB;
③若PA=PB,则点P必是线段AB的垂直平分线上的点;
④若EA=EB,则过点E的直线垂直平分线段AB.
A.1个 B.2个 C.3个 D.4个
C
巩固练习
解:∵ AB =AC,
∴ 点A 在BC 的垂直平分线上.
∵ MB =MC,
∵ 点M 在BC 的垂直平分线上,
∴ 直线AM 是线段BC 的垂直
平分线.
5.如图,AB =AC,MB =MC.直线AM 是线段BC 的垂直平分线吗?
A
B
C
D
M
典例讲解
例2、如何用尺规作图的方法经过直线外一点作已知直线的垂线?
C
A
B
D
K
F
E
作法:
(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C为圆心,CK长为半径作弧,交AB于点
D和E.
(3)分别以点D和点E为圆心,大于 的长
为半径作弧,两弧相交于点F.
(4)作直线CF.
直线CF就是所求作的垂线.
(1)为什么任意取一点K ,使点K与点C 在直线两旁?
(2)为什么要以大于 的长为半径作弧?
(3)为什么直线CF 就是所求作的垂线?
想一想
课堂总结
线段的垂直平分线
性质
线段垂直平分线上的点与这条线段两个端点的距离相等
判定
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上
集合
定义
线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是与线段两个端点距离相等的所有点的集合
关系
PA=PB
点P在线段AB的垂直平分线上
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上
线段垂直平分线上的点与这条线段两个端点的距离相等
拓展提高
1. 如图,点A,B,C表示某公司三个车间的位置,现要建一个仓库,要求它到三个车间的距离相等,则仓库应建在什么位置?
答:△ABC 三边垂直平分线的交点上.
拓展提高
2.如图,已知AB比AC长2 cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是14 cm,求AB和AC的长.
解:∵DE垂直平分BC,
∴DB=DC.
∵AC+AD+DC=14 cm,
∴AC+AD+BD=14 cm.
即AC+AB=14 cm.
设AB=x cm,AC=y cm.
根据题意,得 解得
∴AB长为8 cm,AC长为6 cm.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
13.1.2线段的垂直平分线的性质(1)
人教版八年级上册
教学目标
1、理解线段垂直平分线的性质和判定.能够证明线段垂直平分线的性质定理、判定定理及进行应用;能够利用尺规过直线外一点作该直线的垂线.
2、经历探索、猜测、证明的过程,进一步发展学生的推理证明意识和能力.
3、在数学活动中体会获得成功的体验,锻炼克服困难的意志,建立学习的自信心.
复习回顾
如果一个平面图形沿一条直线 .直线两旁的部分能够 ,这个图形就叫做轴对称图形.折痕所在的这条直线叫做_________.
对称轴
折叠
互相重合
忆一忆
把一个图形沿着某一条直线_______,如果它能够______________________,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做_______________.
折叠
与另一个图形重合
对称点
新知讲解
知识点1
线段垂直平分线的性质
探究
如图,直线 l 垂直平分线段 AB,P1,P2,P3,…是 l 上的点,分别量一量点 P1,P2,P3,… 到点 A 与点 B 的距离,你有什么发现?
A
B
l
P1
P2
P3
你能用不同的方法验证这一结论吗?
相等.
新知讲解
猜想:“线段垂直平分线上的点到线段两端点的距离相等.”
已知:如图,直线l⊥AB,垂足为C,AC=CB,点P 在l 上.
求证:PA =PB.
A
B
P
C
l
新知讲解
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
A
B
P
C
l
新知讲解
线段垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离相等.
用符号语言表示为:
∵ CA =CB,l⊥AB,∴ PA =PB.
A
B
P
C
l
巩固练习
1.如图,NM是线段AB的垂直平分线,下列说
法正确的有: .
①AB⊥MN,②AD=DB, ③MN⊥AB,
④MD=DN,⑤AB是MN的垂直平分线.
A
B
M
N
D
①②③
巩固练习
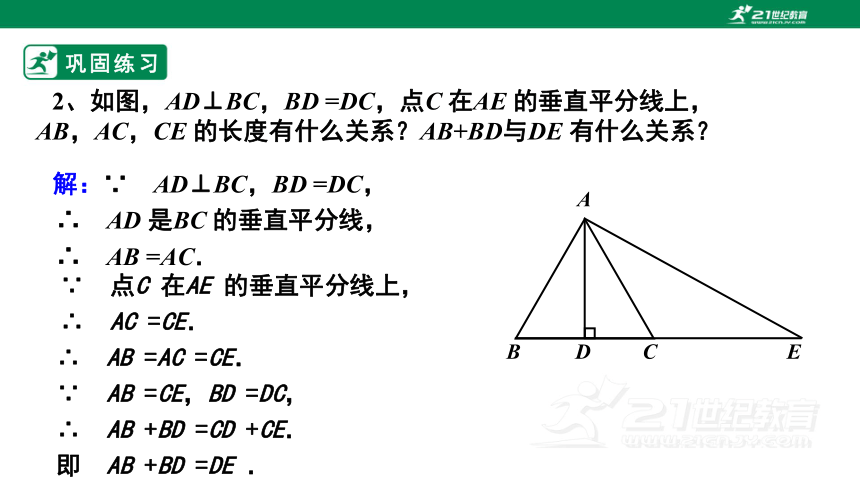
解:∵ AD⊥BC,BD =DC,
∴ AD 是BC 的垂直平分线,
∴ AB =AC.
2、如图,AD⊥BC,BD =DC,点C 在AE 的垂直平分线上,AB,AC,CE 的长度有什么关系?AB+BD与DE 有什么关系?
∴ AB =AC =CE.
∵ AB =CE,BD =DC,
∴ AB +BD =CD +CE.
即 AB +BD =DE .
∵ 点C 在AE 的垂直平分线上,
∴ AC =CE.
A
B
C
D
E
巩固练习
3.在△ABC中,∠ACB=90°,AB=8cm,BC的垂直平分线DE交AB于D点,则CD=_____ .
4cm
4.在△ABC,PM,QN分别垂直平分AB,AC,则:
(1)若BC=10cm则△APQ的周长=_____cm;
(2)若∠BAC=100°则∠PAQ=______.
10
20°
新知讲解
反过来,如果PA =PB,那么点P 是否在线段AB 的垂直平分线上呢?
点P 在线段AB 的垂直平分线上.
知识点2
线段垂直平分线的判定
新知讲解
已知:如图,在△ABP中,PA =PB.
求证:点P 在线段AB 的垂直平分线上.
P
A
B
C
证明:过点P 作线段AB 的垂线PC,垂足为C.
则∠PCA =∠PCB=90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,∴ 点P 在线段AB 的垂直平分线上.
新知讲解
用数学符号表示为:
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上.
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
P
A
B
C
典例讲解
例1、如图,已知在△ABC中,ON是AB的垂直平分线,并且OA=OC.
求证:点O在 BC的垂直平分线上.
A
B
C
O
N
∴点O在BC的垂直平分线上.(到一条线段的两个端点距离相等的点,在这条线段的垂直平分线上)
证明:连接OB.
∵ ON是AB的垂直平分线,(已知)
∴ OA=OB.(线段的垂直平分线上的点到这条线段的两个端点的距离相等)
∵ OA=OC,(已知)
∴ OB=OC.(等量代换)
巩固练习
A
B
M
N
D
4.下列说法正确的个数有( )
①若直线PE是线段AB的垂直平分线,则EA=EB,PA=PB;
②若PA=PB,EA=EB,则直线PE垂直平分线段AB;
③若PA=PB,则点P必是线段AB的垂直平分线上的点;
④若EA=EB,则过点E的直线垂直平分线段AB.
A.1个 B.2个 C.3个 D.4个
C
巩固练习
解:∵ AB =AC,
∴ 点A 在BC 的垂直平分线上.
∵ MB =MC,
∵ 点M 在BC 的垂直平分线上,
∴ 直线AM 是线段BC 的垂直
平分线.
5.如图,AB =AC,MB =MC.直线AM 是线段BC 的垂直平分线吗?
A
B
C
D
M
典例讲解
例2、如何用尺规作图的方法经过直线外一点作已知直线的垂线?
C
A
B
D
K
F
E
作法:
(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C为圆心,CK长为半径作弧,交AB于点
D和E.
(3)分别以点D和点E为圆心,大于 的长
为半径作弧,两弧相交于点F.
(4)作直线CF.
直线CF就是所求作的垂线.
(1)为什么任意取一点K ,使点K与点C 在直线两旁?
(2)为什么要以大于 的长为半径作弧?
(3)为什么直线CF 就是所求作的垂线?
想一想
课堂总结
线段的垂直平分线
性质
线段垂直平分线上的点与这条线段两个端点的距离相等
判定
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上
集合
定义
线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是与线段两个端点距离相等的所有点的集合
关系
PA=PB
点P在线段AB的垂直平分线上
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上
线段垂直平分线上的点与这条线段两个端点的距离相等
拓展提高
1. 如图,点A,B,C表示某公司三个车间的位置,现要建一个仓库,要求它到三个车间的距离相等,则仓库应建在什么位置?
答:△ABC 三边垂直平分线的交点上.
拓展提高
2.如图,已知AB比AC长2 cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是14 cm,求AB和AC的长.
解:∵DE垂直平分BC,
∴DB=DC.
∵AC+AD+DC=14 cm,
∴AC+AD+BD=14 cm.
即AC+AB=14 cm.
设AB=x cm,AC=y cm.
根据题意,得 解得
∴AB长为8 cm,AC长为6 cm.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
