12.2.2正比例函数的图象与性质 课件(共22张PPT)
文档属性
| 名称 | 12.2.2正比例函数的图象与性质 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 17:29:22 | ||
图片预览



文档简介
(共22张PPT)
1.正比例函数的定义
一般地,形如 y=kx(k为常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数
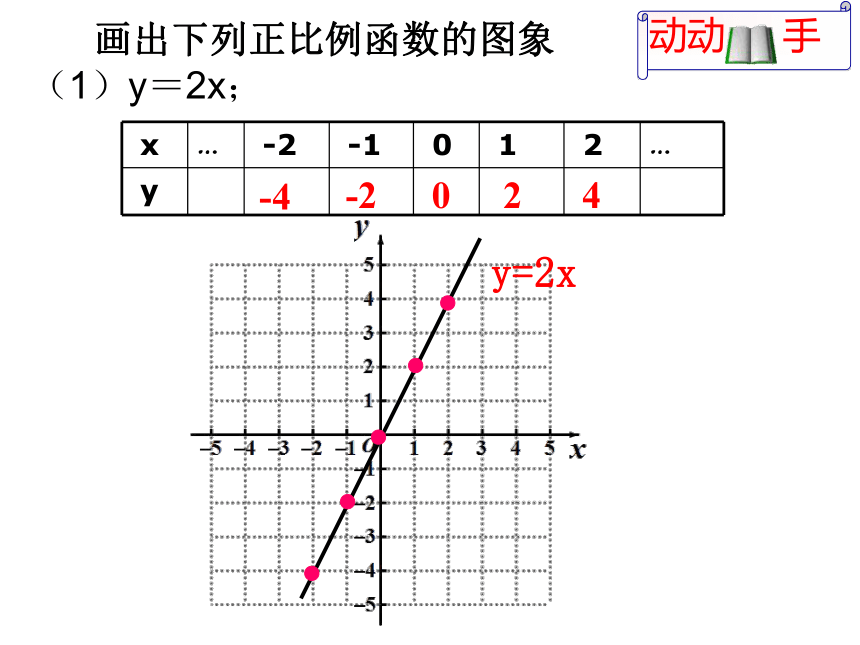
2.画函数图象的步骤有哪些?
列表、描点、连线
温故知新
12.2.2正比例函数的
图象与性质
-4
-2
0
2
4
x … -2 -1 0 1 2 …
y
动动 手
y=2x
画出下列正比例函数的图象 (1)y=2x;
动动 手
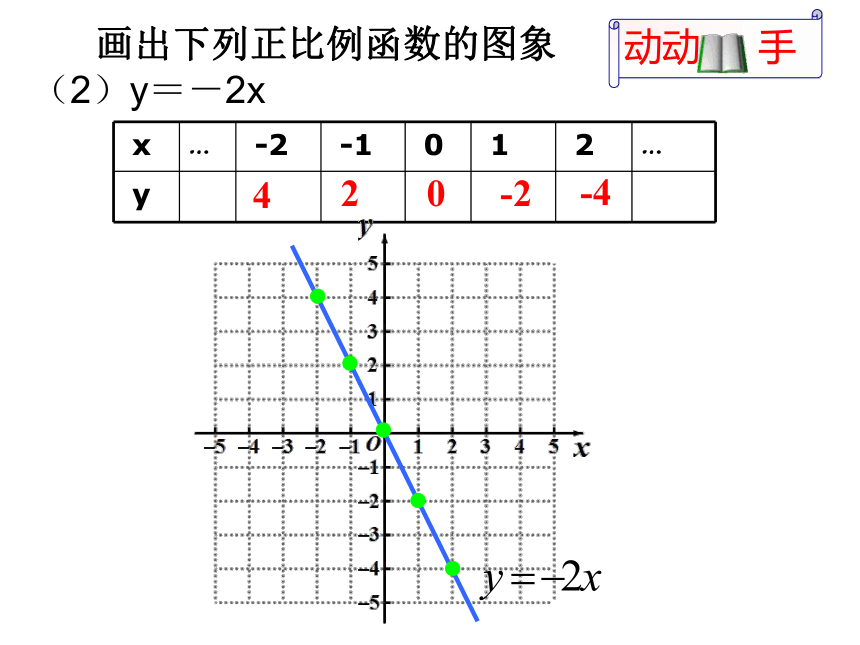
画出下列正比例函数的图象 (2)y=-2x
4
2
0
-2
-4
x … -2 -1 0 1 2 …
y
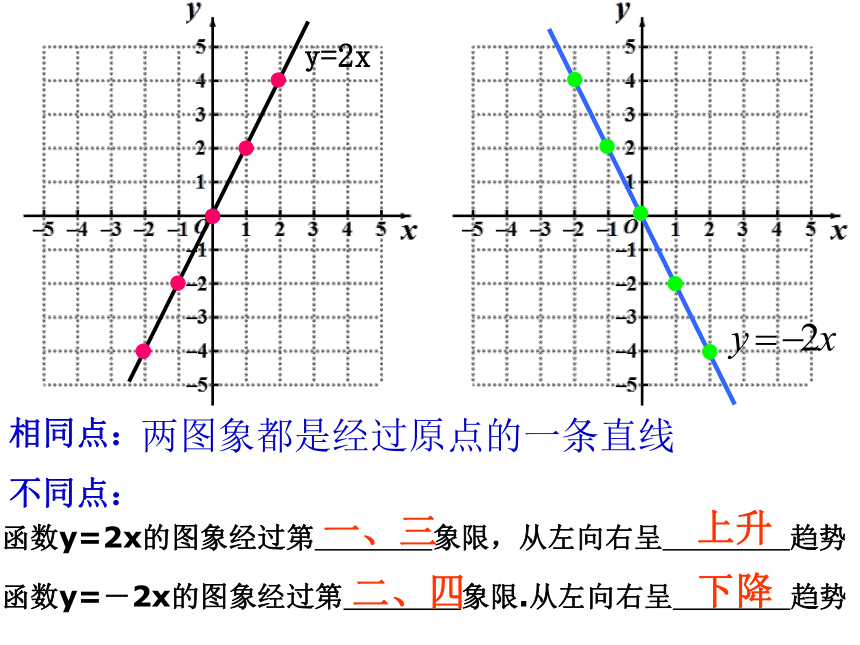
函数y=-2x的图象经过第 象限.从左向右呈 趋势
函数y=2x的图象经过第 象限,从左向右呈 趋势
相同点:
不同点:
上升
一、三
下降
二、四
两图象都是经过原点的一条直线
y=2x
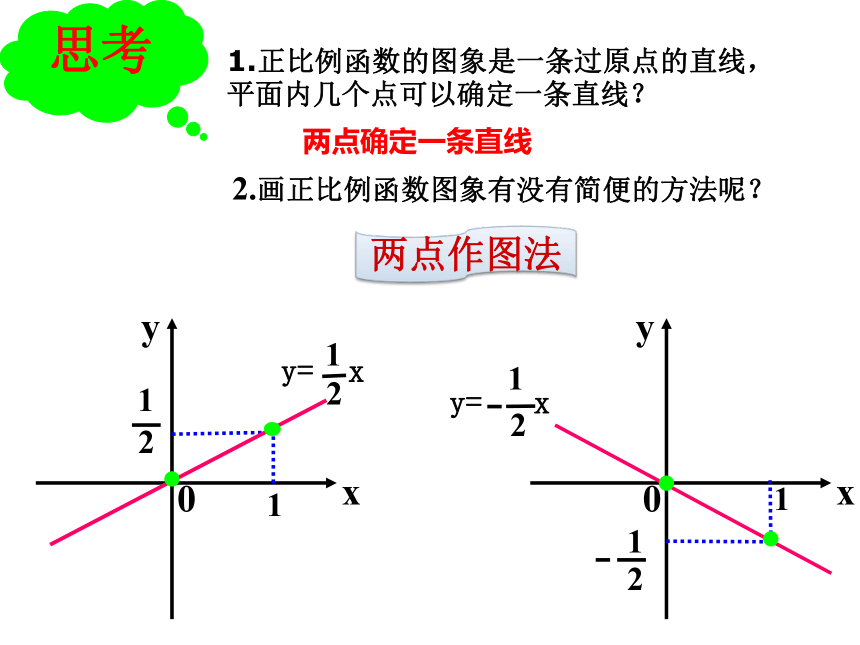
2.画正比例函数图象有没有简便的方法呢?
思考
1.正比例函数的图象是一条过原点的直线,平面内几个点可以确定一条直线?
x
y
0
x
y
0
1
1
y= x
y= x
2
1
2
1
2
1
2
1
两点作图法
两点确定一条直线
分别在同一平面直角坐标系中,画出下列函数的图象 (同桌合作5分钟内完成)
数形结合 动手画图
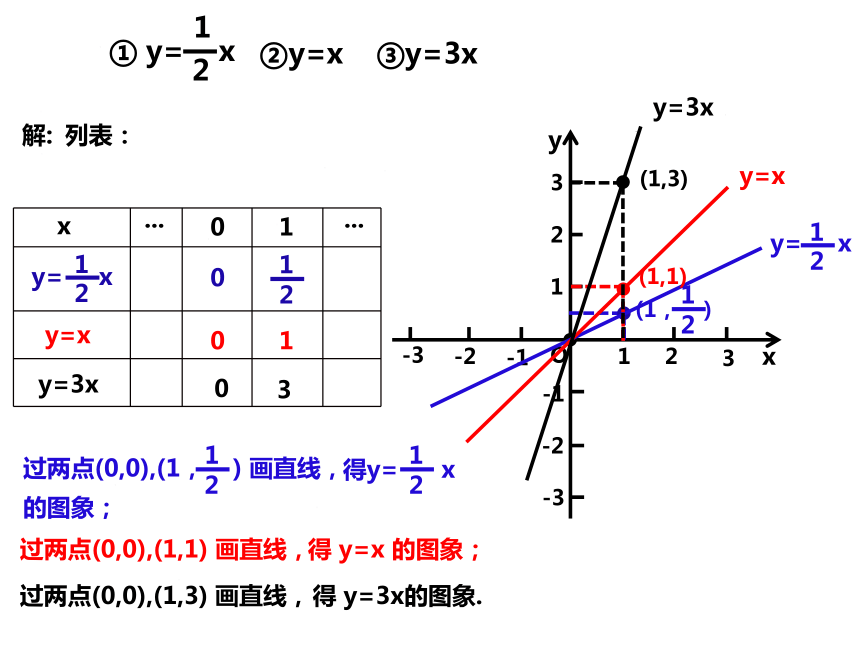
①y= x
②y=x
③y=3x
探究1
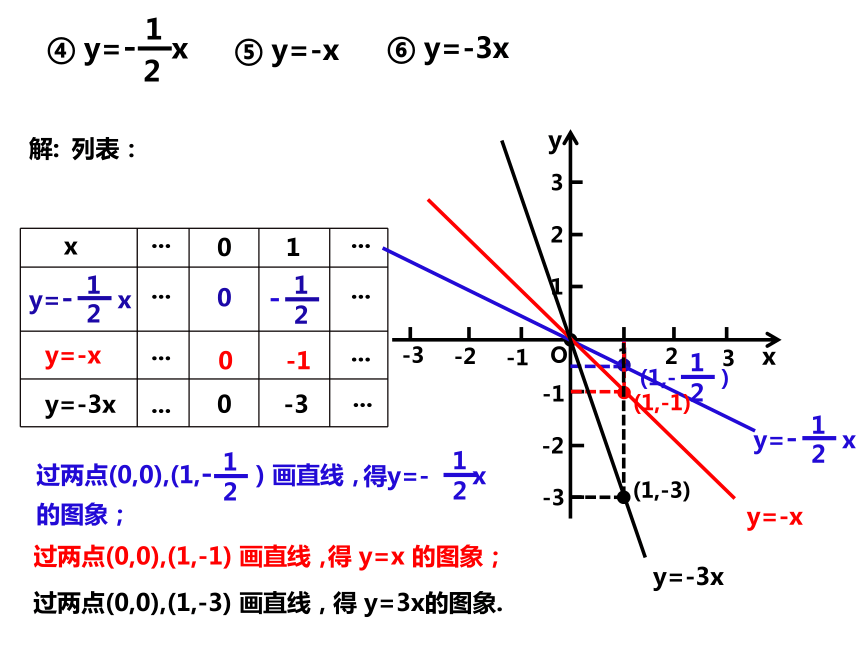
④y= -x
⑤y=-x
⑥y=-3x
得y= x的图象;
O
-1
y
x
1
2
3
3
2
1
-3
-2
-1
-2
-3
① y= x
1
2
②y=x
③y=3x
解:
列表:
...
...
0
1
x
y= x
1
2
y=x
y=3x
0
0
0
1
2
1
3
过两点(0,0),(1, ) 画直线,
1
2
1
2
过两点(0,0),(1,1) 画直线,
得 y=x 的图象;
过两点(0,0),(1,3) 画直线,
得 y=3x的图象.
y= x
1
2
y=x
y=3x
(1, )
1
2
(1,1)
(1,3)
-1
解:
列表:
...
...
...
...
...
...
...
...
0
1
x
y=- x
1
2
y=-x
y=-3x
0
0
0
1
2
-1
-3
-
得y=- x的图象;
过两点(0,0),(1,- ) 画直线,
1
2
1
2
过两点(0,0),(1,-1) 画直线,
得 y=x 的图象;
过两点(0,0),(1,-3) 画直线,
得 y=3x的图象.
O
y
x
1
2
3
3
2
1
-3
-2
-1
-2
-3
(1,- )
1
2
y=- x
1
2
(1,-1)
y=-x
(1,-3)
y=-3x
④ y=- x
1
2
⑤ y=-x
⑥ y=-3x
观察图象,就下面问题思考后回答:
O
-1
y
x
1
2
3
3
2
1
-3
-2
-1
-2
-3
y= x
1
2
y=x
y=3x
(1, )
1
2
(1,1)
(1,3)
-1
O
y
x
1
2
3
3
2
1
-3
-2
-1
-2
-3
(1,- )
1
2
y=- x
1
2
(1,-1)
y=-x
(1,-3)
y=-3x
探究2
O
-1
y
x
1
2
3
3
2
1
-3
-2
-1
-2
-3
y= x
1
2
y=x
y=3x
(1, )
1
2
(1,1)
(1,3)
-1
O
y
x
1
2
3
3
2
1
-3
-2
-1
-2
-3
(1,- )
1
2
y=- x
1
2
(1,-1)
y=-x
(1,-3)
y=-3x
(1) k>0 与k<0时,y=kx 的图象各有什么特点?
k>0
k<0
y=kx 的图象在二、四象限
当k>0时 ,
y=kx 的图象在一、三象限
当k<0时,
O
-1
y
x
1
2
3
3
2
1
-3
-2
-1
-2
-3
y= x
1
2
-1
O
y
x
1
2
3
3
2
1
-3
-2
-1
-2
-3
y=- x
1
2
k>0
k<0
y=kx 的图像在二、四象限;
当k>0时 ,
y=kx 的图像在一、三象限;
y随 x的 增大而增大;
当k<0时,
y随 x 的增大而减小.
(图象是自左向右上升的)
(图象是自左向右下降的)
3
2
1
2
1
2
-
3
2
-
(2) 下列函数中,随着 x 的增大,y 的值分别如何变化
O
-1
y
x
1
2
3
3
2
1
-3
-2
-1
-2
-3
y= x
1
2
y=x
y=3x
(1, )
1
2
(1,1)
(1,3)
-1
O
y
x
1
2
3
3
2
1
-3
-2
-1
-2
-3
(1,- )
1
2
y=- x
1
2
(1,-1)
y=-x
(1,-3)
y=-3x
3
1
1
2
3
1
1
2
(3)│k│的大小不同,对 y=kx 的图象有什么影响?
│k│越大,
│k│越小,
y=kx的图象就越靠近x轴 .
y=kx 的图象就越靠近y轴;
(2) 当k>0时,y=kx的图象经过一、三象限,从左向右呈上升趋势, y随着自变量x的增大 而增大。
(3) 当k<0时,y=kx的图象过经过第二、四象限,从左向右呈下降趋势, y随x的增大而减小。
O
1
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
x
y
O
1
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
x
y
总结
(1)图象经过原点
1.由正比例函数解析式(根据k的正、负),来判断其函数图像分布在哪些象限
一、三象限
一、三象限
二、四象限
1.由函数解析式,请你说出下列函数的变化情况
y随x的增大而增大
y随x的增大而增大
y随x的增大而减小
看谁反应快
(1) 若函数图象经过第一、三象限,则 k 的取值范围是 .
2. 已知正比例函数 y=(k+1)x.
(2) 若函数值 y 随 x 的增大而减小,则 k 的取值范围是 .
基础闯关
K>-1
K<-1
3.函数 y=(k2+3)x 的图象经过第 象限内,经过点(0, )与点 (1, ),y 随 x 的增大而 .
一、三
增大
0
k2+3
变式 若图像经过点(x1,y1)和(x2,y2), 若 x1则 y1 y2.
小试身手
<
4、已知直线 y=(2-3m)x 经过点 A(x1,y1) 和点 B(x2,y2),当 x1y2,则该直线经过第 象限,m 的取值范围是 .
二、四
举一反三
m>
5.如图,三个正比例函数的图像分别对应的解析式是 ①y=ax;② y=bx;③ y=cx; ④y=dx.则a,b,c,d的大小关系是( )
A. aB. bC. bD. ax
y
①
②
③
B
活学活用
④
挑战一下
1、正比例函数y=kx的图象是经过(0,0)(1,k)的一条直线,
我们把正比例函数y=kx的图象叫做直线y=kx;
2、正比例函数y=kx的图象的画法;
3、正比例函数的性质:
(1)图象都经过原点;
(2)当k>0时,它的图象从左向右上升,经过第一、二象限,y随x的增大而增大;
当k<0时,它的图象从左向右下降,经过第二、四象限,y随x的增大而减少。
分享收获 课堂小结
1.正比例函数的定义
一般地,形如 y=kx(k为常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数
2.画函数图象的步骤有哪些?
列表、描点、连线
温故知新
12.2.2正比例函数的
图象与性质
-4
-2
0
2
4
x … -2 -1 0 1 2 …
y
动动 手
y=2x
画出下列正比例函数的图象 (1)y=2x;
动动 手
画出下列正比例函数的图象 (2)y=-2x
4
2
0
-2
-4
x … -2 -1 0 1 2 …
y
函数y=-2x的图象经过第 象限.从左向右呈 趋势
函数y=2x的图象经过第 象限,从左向右呈 趋势
相同点:
不同点:
上升
一、三
下降
二、四
两图象都是经过原点的一条直线
y=2x
2.画正比例函数图象有没有简便的方法呢?
思考
1.正比例函数的图象是一条过原点的直线,平面内几个点可以确定一条直线?
x
y
0
x
y
0
1
1
y= x
y= x
2
1
2
1
2
1
2
1
两点作图法
两点确定一条直线
分别在同一平面直角坐标系中,画出下列函数的图象 (同桌合作5分钟内完成)
数形结合 动手画图
①y= x
②y=x
③y=3x
探究1
④y= -x
⑤y=-x
⑥y=-3x
得y= x的图象;
O
-1
y
x
1
2
3
3
2
1
-3
-2
-1
-2
-3
① y= x
1
2
②y=x
③y=3x
解:
列表:
...
...
0
1
x
y= x
1
2
y=x
y=3x
0
0
0
1
2
1
3
过两点(0,0),(1, ) 画直线,
1
2
1
2
过两点(0,0),(1,1) 画直线,
得 y=x 的图象;
过两点(0,0),(1,3) 画直线,
得 y=3x的图象.
y= x
1
2
y=x
y=3x
(1, )
1
2
(1,1)
(1,3)
-1
解:
列表:
...
...
...
...
...
...
...
...
0
1
x
y=- x
1
2
y=-x
y=-3x
0
0
0
1
2
-1
-3
-
得y=- x的图象;
过两点(0,0),(1,- ) 画直线,
1
2
1
2
过两点(0,0),(1,-1) 画直线,
得 y=x 的图象;
过两点(0,0),(1,-3) 画直线,
得 y=3x的图象.
O
y
x
1
2
3
3
2
1
-3
-2
-1
-2
-3
(1,- )
1
2
y=- x
1
2
(1,-1)
y=-x
(1,-3)
y=-3x
④ y=- x
1
2
⑤ y=-x
⑥ y=-3x
观察图象,就下面问题思考后回答:
O
-1
y
x
1
2
3
3
2
1
-3
-2
-1
-2
-3
y= x
1
2
y=x
y=3x
(1, )
1
2
(1,1)
(1,3)
-1
O
y
x
1
2
3
3
2
1
-3
-2
-1
-2
-3
(1,- )
1
2
y=- x
1
2
(1,-1)
y=-x
(1,-3)
y=-3x
探究2
O
-1
y
x
1
2
3
3
2
1
-3
-2
-1
-2
-3
y= x
1
2
y=x
y=3x
(1, )
1
2
(1,1)
(1,3)
-1
O
y
x
1
2
3
3
2
1
-3
-2
-1
-2
-3
(1,- )
1
2
y=- x
1
2
(1,-1)
y=-x
(1,-3)
y=-3x
(1) k>0 与k<0时,y=kx 的图象各有什么特点?
k>0
k<0
y=kx 的图象在二、四象限
当k>0时 ,
y=kx 的图象在一、三象限
当k<0时,
O
-1
y
x
1
2
3
3
2
1
-3
-2
-1
-2
-3
y= x
1
2
-1
O
y
x
1
2
3
3
2
1
-3
-2
-1
-2
-3
y=- x
1
2
k>0
k<0
y=kx 的图像在二、四象限;
当k>0时 ,
y=kx 的图像在一、三象限;
y随 x的 增大而增大;
当k<0时,
y随 x 的增大而减小.
(图象是自左向右上升的)
(图象是自左向右下降的)
3
2
1
2
1
2
-
3
2
-
(2) 下列函数中,随着 x 的增大,y 的值分别如何变化
O
-1
y
x
1
2
3
3
2
1
-3
-2
-1
-2
-3
y= x
1
2
y=x
y=3x
(1, )
1
2
(1,1)
(1,3)
-1
O
y
x
1
2
3
3
2
1
-3
-2
-1
-2
-3
(1,- )
1
2
y=- x
1
2
(1,-1)
y=-x
(1,-3)
y=-3x
3
1
1
2
3
1
1
2
(3)│k│的大小不同,对 y=kx 的图象有什么影响?
│k│越大,
│k│越小,
y=kx的图象就越靠近x轴 .
y=kx 的图象就越靠近y轴;
(2) 当k>0时,y=kx的图象经过一、三象限,从左向右呈上升趋势, y随着自变量x的增大 而增大。
(3) 当k<0时,y=kx的图象过经过第二、四象限,从左向右呈下降趋势, y随x的增大而减小。
O
1
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
x
y
O
1
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
1
2
3
4
x
y
总结
(1)图象经过原点
1.由正比例函数解析式(根据k的正、负),来判断其函数图像分布在哪些象限
一、三象限
一、三象限
二、四象限
1.由函数解析式,请你说出下列函数的变化情况
y随x的增大而增大
y随x的增大而增大
y随x的增大而减小
看谁反应快
(1) 若函数图象经过第一、三象限,则 k 的取值范围是 .
2. 已知正比例函数 y=(k+1)x.
(2) 若函数值 y 随 x 的增大而减小,则 k 的取值范围是 .
基础闯关
K>-1
K<-1
3.函数 y=(k2+3)x 的图象经过第 象限内,经过点(0, )与点 (1, ),y 随 x 的增大而 .
一、三
增大
0
k2+3
变式 若图像经过点(x1,y1)和(x2,y2), 若 x1
小试身手
<
4、已知直线 y=(2-3m)x 经过点 A(x1,y1) 和点 B(x2,y2),当 x1
二、四
举一反三
m>
5.如图,三个正比例函数的图像分别对应的解析式是 ①y=ax;② y=bx;③ y=cx; ④y=dx.则a,b,c,d的大小关系是( )
A. a
y
①
②
③
B
活学活用
④
挑战一下
1、正比例函数y=kx的图象是经过(0,0)(1,k)的一条直线,
我们把正比例函数y=kx的图象叫做直线y=kx;
2、正比例函数y=kx的图象的画法;
3、正比例函数的性质:
(1)图象都经过原点;
(2)当k>0时,它的图象从左向右上升,经过第一、二象限,y随x的增大而增大;
当k<0时,它的图象从左向右下降,经过第二、四象限,y随x的增大而减少。
分享收获 课堂小结
