19.2.1矩形的性质
图片预览





文档简介
课件39张PPT。19.2 特殊的平行四边形两组对边
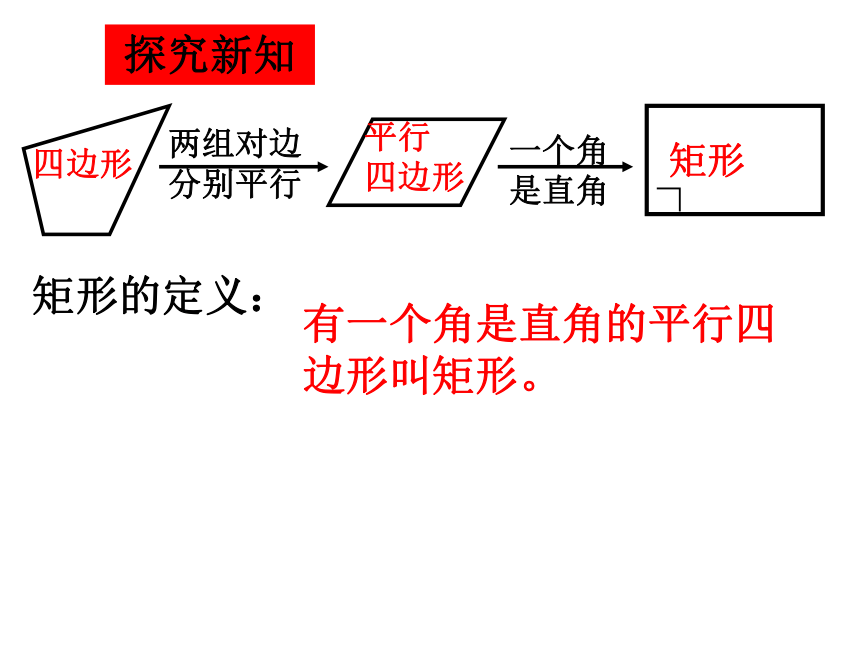
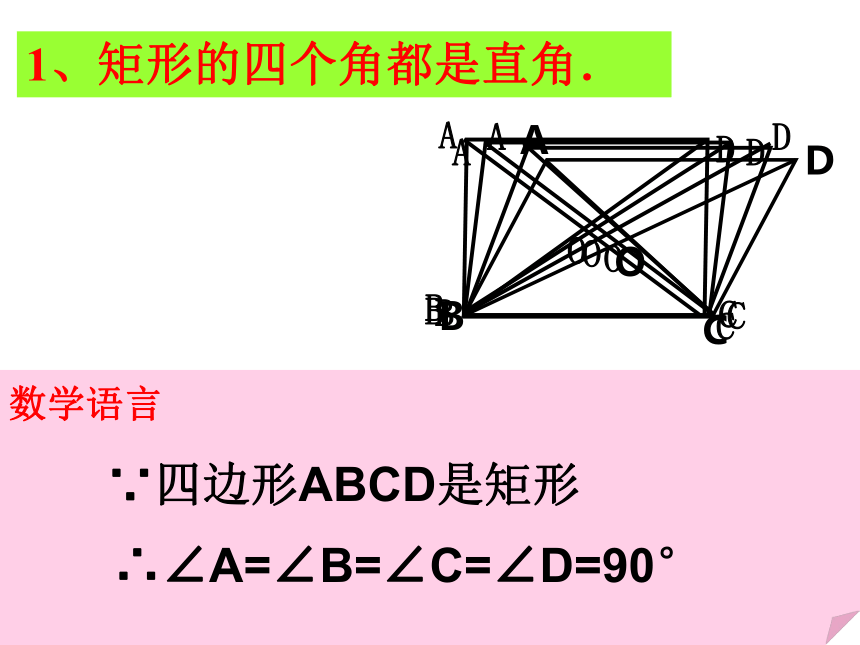
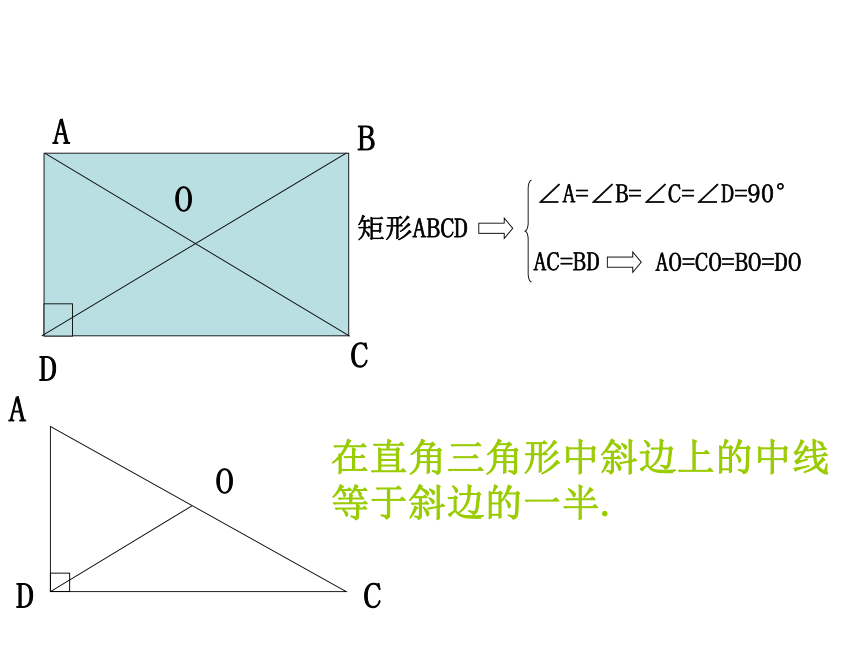
分别平行四边形平行四边形的性质有:边: 对边平行且相等角:对角相等;邻角互补对角线:对角线互相平分回忆 19.2.1 矩形有一个角是直角的平行四边形叫矩形。探究新知矩形的定义:1、矩形的四个角都是直角.数学语言∵四边形ABCD是矩形 ∴∠A=∠B=∠C=∠D=90°已知:四边形ABCD是矩形
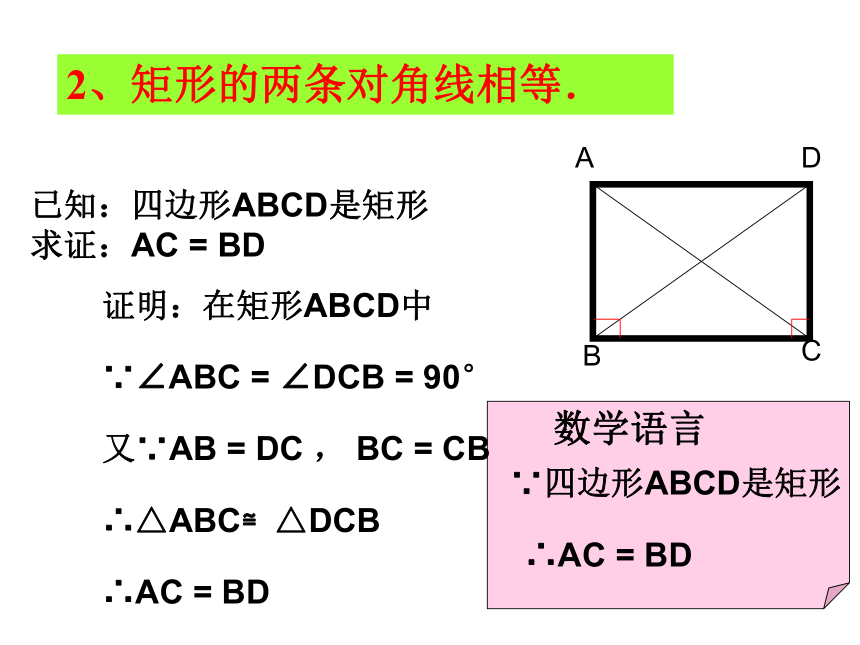
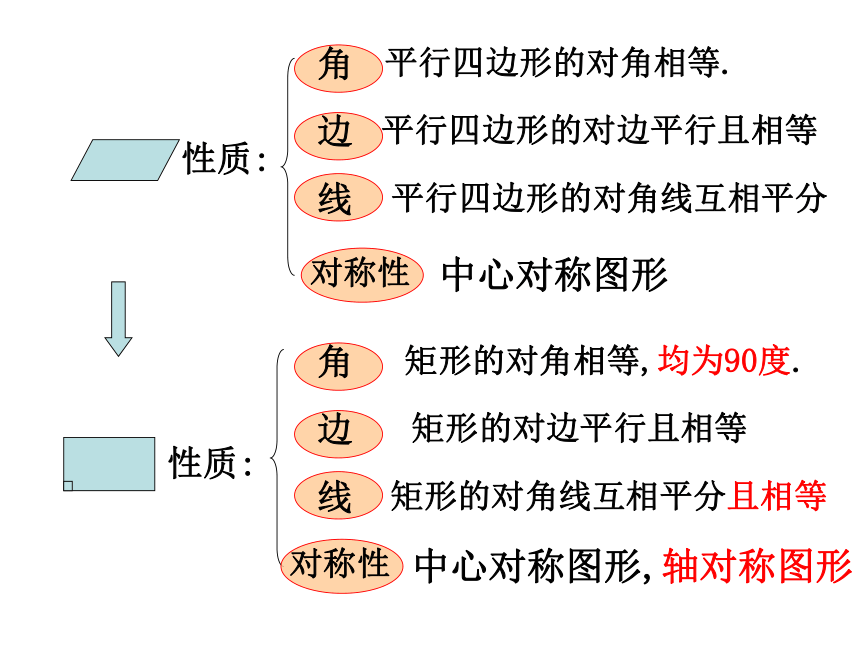
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD2、矩形的两条对角线相等.数学语言∵四边形ABCD是矩形 ∴AC = BD请你总结矩形的有关性质矩形的四个角都是直角.矩形的两条对角线相等.从角上看:从对角线上看:角边线平行四边形的对角相等.平行四边形的对边平行且相等平行四边形的对角线互相平分矩形的对角相等,均为90度.矩形的对边平行且相等矩形的对角线互相平分且相等对称性中心对称图形角边线对称性中心对称图形,轴对称图形矩形ABCD∠A=∠B=∠C=∠D=90°AC=BDAO=CO=BO=DO在直角三角形中斜边上的中线
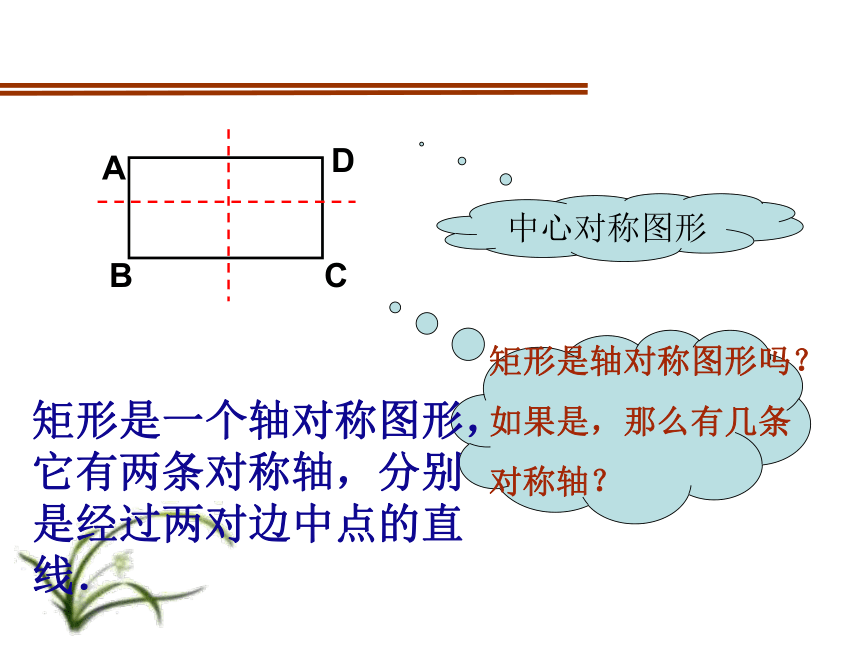
等于斜边的一半.矩形是轴对称图形吗?
如果是,那么有几条
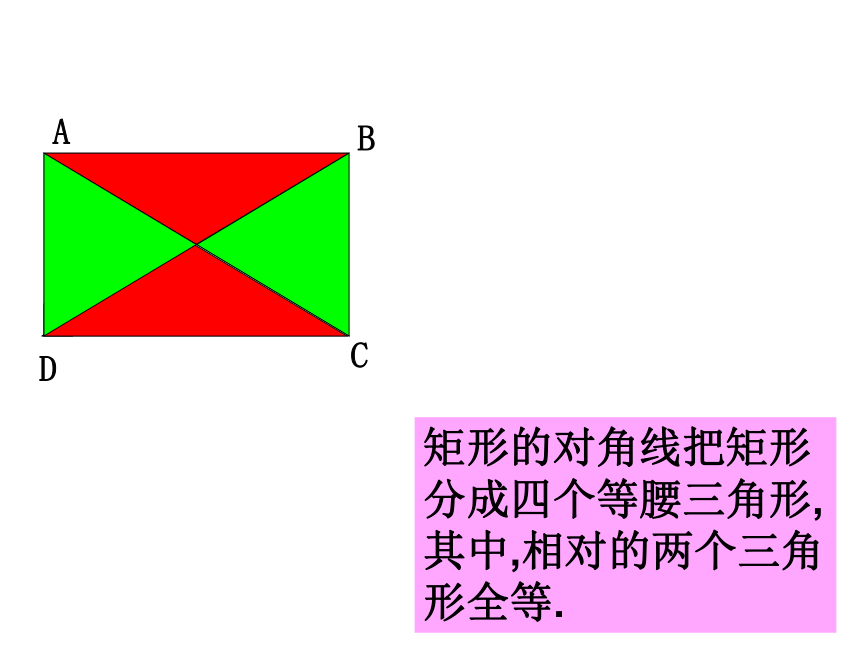
对称轴?矩形是一个轴对称图形,它有两条对称轴,分别是经过两对边中点的直线.中心对称图形ABCDO矩形的对角线把矩形分成四个等腰三角形,其中,相对的两个三角形全等.(1)矩形具有而平行四边形不具有的性质( )
(A)内角和是360度(B)对角相等
(C)对边平行且相等(D)对角线相等 (2)下面性质中,矩形不一定具有的是( )
(A)对角线相等(B)四个角相等
(C)是轴对称图形(D)对角线垂直(3)由已知矩形的一个顶点向其所对的对角线引垂线,该垂线分直角为3:1两部分,则垂线与另一条对角线的夹角是( )
(A)50度(B)45度(C)30度(D)22.5度DDB如图,在矩形ABCD中,AC与BD相交于点O,AB=3cm,BC=4cm 则AC= cm,
AO= cm,BO= cm. 52.5 2.54A开动脑筋 如图,在△ABC中,D,E,F,分别是BC、AC、AB边的中点,AH⊥BC于H,FD=8㎝,则HE=8㎝已知:在△ABC中∠ACB=90°,AD = BD证明:延长CD到E使DE=CD,连 结AE、BE.∵AD = BD ,CD = EDE∴ACBE是平行四边形又∵∠ACB = 90∴CE = AB由于CD= CE
∴ CD = AB求证:CD = AB3.矩形是轴对称图形.1.直角三角形斜边上的中线等于斜边的一半再探新知DOCBA2.矩形的对角线把矩形分成两对全等的等腰三角形有一个角是直角的
平行四边形叫矩形2.矩形的性质:对边平行且相等四个角都是直角对角线互相平分 且相等1.矩形的定义:5.矩形是轴对称图形.3.直角三角形斜边上的中线等于斜边的一半4. 矩形的对角线把矩形分成两对全等的
等腰三角形总结归纳你还知道矩形的其他性质吗?例: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长? 解:∵ 四边形ABCD是矩形
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形
∴ OA=AB=4(㎝)
∴ 矩形的对角线长 AC=BD=2OA=8(㎝)O已知对角线长是8cm,两对角线的一个夹角是120°, 求矩形的边长.变式:如果矩形两对角线的夹角是60°或120°,则其中必有等边三角形. 学海 无涯1.矩形具有而一般平行四边形不具有的性质是( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分2.下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角相等
C.是轴对称图形 D.对角线互相垂直AD四边形ABCD是矩形
2.若已知AB=8㎝,AD=6㎝,
则AC= _____㎝ OB=____ ㎝
3.若已知∠CAB=40°,则∠OCB=____
∠OBA=____ ∠AOB=_____ ∠AOD=____
4.若已知AC=10㎝,BC=6㎝,则矩形的周长=____㎝矩形的面积=____ ㎝2
5. 若已知 ∠DOC=120°,AD=6㎝.则AC= ___ ㎝550°10100°40°12482880°练一练6.如图:在矩形ABCD中,两条对角线AC、BD相交于点O, AB=OA=4cm.
则BD=____,AD=_____
ABOCD7.如图,用8块相同的长方形地砖拼成一个矩形地面,则每块长方形地砖的长和宽分别是( )
(A)48cm,12cm; (B)48cm,16cm;
(C)44cm,16cm; (D)45cm,15cm.D(1)矩形具有而平行四边形不具有的性质( )
(A)内角和是360度(B)对角相等(C)对边平行且相等(D)对角线相等 (2)下面性质中,矩形不一定具有的是( )
(A)对角线相等(B)四个角相等(C)是轴对称图形(D)对角线垂直
(3)由已知矩形的一个顶点向其所对的对角线引垂线,该垂线分直角为3:1两部分,则垂线与另一条对角线的夹角是( )
(A)50度(B)45度(C)30度(D)22.5度
DDB课堂练习 4. 过四边形的各个顶点分别作对角线的平行线,若这四
条平行线围成一个矩形,则原四边形一定是 课堂练习A.对角线相等的四边形 B.对角线互相平分且相等的四边形
C.对角线互垂直平分的四边形 D.对角线垂直的四边形5. 已知矩形的一条对角线与一边的夹角是40°,则两
条对角线所夹锐角的度数为 A.50° B.60° C.70° D.80°6. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,
则∠BAE等于 A.30° B.45° C.60° D.120°[ ][ ][ ]DDA 学海 无涯A3.在 中,斜边AC上的中线
和高分别是6cm和5cm,则 的
面积S=( )。 A
BCDE30cm2600如图,矩形ABCD的两条对角线相交于点O,AB=4cm,∠AOB=60°,求矩形对角线的长。解:∵四边形ABCD是矩形,∴AC与BD相等且互相平分。又 ∠AOB=60°,∴ ΔOAB是等边三角形∴OA=AB=4(cm)∴ AC=BD = 2OA=2×4=8(cm)
∴ OA = OB。变式:若BD=8cm,∠AOD=120°,求边AB的长。
O1200例1:如图:在矩形ABCD中,两条对角线AC、BD相交于点O, AB=OA=4cm.
求:BD与AD的长
ABOCD例2:已知:如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AB=4cm,求矩形对角线的长.ABOCD随堂练习1. 矩形具有而一般平行四边形不具有的性质是( ).
A 对角线相等 B 对边相等
C 对角相等 D 对角线互相平分 A2.在矩形ABCD中,
AE⊥BD于E,若
BE=OE=1,则
AC= , AB=---BCDEAO423.如图,用8块相同的长方形地砖拼成一个矩形地面,则每块长方形地砖的长和宽分别是( )
(A)48cm,12cm; (B)48cm,16cm;
(C)44cm,16cm; (D)45cm,15cm.D(2).矩形的两条对角线将矩形分成四个面积
相等的等腰三角形( )(1).矩形是平行四边形( )4.矩形的短边长为3cm,两对角线所成的角是60 °,则它的另一边长是_______.5. 已知矩形对角线长为4cm,一边长为 cm,
则矩形的面积是________.6.判断题拓展与应用例. 如图,在矩形ABCD中,DE平分∠ADC交AC于E,交BC于F,若∠BDF=150,求∠COF的度数.ABOCDEF拓展与应用练习如图:在ABCD矩形中AB=6cm,BC=8cm,
将矩形折叠,
使B点与点D重合,
求折痕EF的长。ABOCDA/EF有一个角是直角的
平行四边形叫矩形2.矩形的性质:对边平行且相等四个角都是直角对角线互相平分 且相等1.矩形的定义:5.矩形是轴对称图形.3.直角三角形斜边上的中线等于斜边的一半4. 矩形的对角线把矩形分成两对全等的
等腰三角形总结矩形与平行四边形的性质对比两对角线相等且互相平分两条对角线互相平分对角线对角相等,都是90°对角相等角两组对边平行且相等两组对边平行且相等边矩形平行四边形性质2013年6月
分别平行四边形平行四边形的性质有:边: 对边平行且相等角:对角相等;邻角互补对角线:对角线互相平分回忆 19.2.1 矩形有一个角是直角的平行四边形叫矩形。探究新知矩形的定义:1、矩形的四个角都是直角.数学语言∵四边形ABCD是矩形 ∴∠A=∠B=∠C=∠D=90°已知:四边形ABCD是矩形
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD2、矩形的两条对角线相等.数学语言∵四边形ABCD是矩形 ∴AC = BD请你总结矩形的有关性质矩形的四个角都是直角.矩形的两条对角线相等.从角上看:从对角线上看:角边线平行四边形的对角相等.平行四边形的对边平行且相等平行四边形的对角线互相平分矩形的对角相等,均为90度.矩形的对边平行且相等矩形的对角线互相平分且相等对称性中心对称图形角边线对称性中心对称图形,轴对称图形矩形ABCD∠A=∠B=∠C=∠D=90°AC=BDAO=CO=BO=DO在直角三角形中斜边上的中线
等于斜边的一半.矩形是轴对称图形吗?
如果是,那么有几条
对称轴?矩形是一个轴对称图形,它有两条对称轴,分别是经过两对边中点的直线.中心对称图形ABCDO矩形的对角线把矩形分成四个等腰三角形,其中,相对的两个三角形全等.(1)矩形具有而平行四边形不具有的性质( )
(A)内角和是360度(B)对角相等
(C)对边平行且相等(D)对角线相等 (2)下面性质中,矩形不一定具有的是( )
(A)对角线相等(B)四个角相等
(C)是轴对称图形(D)对角线垂直(3)由已知矩形的一个顶点向其所对的对角线引垂线,该垂线分直角为3:1两部分,则垂线与另一条对角线的夹角是( )
(A)50度(B)45度(C)30度(D)22.5度DDB如图,在矩形ABCD中,AC与BD相交于点O,AB=3cm,BC=4cm 则AC= cm,
AO= cm,BO= cm. 52.5 2.54A开动脑筋 如图,在△ABC中,D,E,F,分别是BC、AC、AB边的中点,AH⊥BC于H,FD=8㎝,则HE=8㎝已知:在△ABC中∠ACB=90°,AD = BD证明:延长CD到E使DE=CD,连 结AE、BE.∵AD = BD ,CD = EDE∴ACBE是平行四边形又∵∠ACB = 90∴CE = AB由于CD= CE
∴ CD = AB求证:CD = AB3.矩形是轴对称图形.1.直角三角形斜边上的中线等于斜边的一半再探新知DOCBA2.矩形的对角线把矩形分成两对全等的等腰三角形有一个角是直角的
平行四边形叫矩形2.矩形的性质:对边平行且相等四个角都是直角对角线互相平分 且相等1.矩形的定义:5.矩形是轴对称图形.3.直角三角形斜边上的中线等于斜边的一半4. 矩形的对角线把矩形分成两对全等的
等腰三角形总结归纳你还知道矩形的其他性质吗?例: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长? 解:∵ 四边形ABCD是矩形
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形
∴ OA=AB=4(㎝)
∴ 矩形的对角线长 AC=BD=2OA=8(㎝)O已知对角线长是8cm,两对角线的一个夹角是120°, 求矩形的边长.变式:如果矩形两对角线的夹角是60°或120°,则其中必有等边三角形. 学海 无涯1.矩形具有而一般平行四边形不具有的性质是( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分2.下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角相等
C.是轴对称图形 D.对角线互相垂直AD四边形ABCD是矩形
2.若已知AB=8㎝,AD=6㎝,
则AC= _____㎝ OB=____ ㎝
3.若已知∠CAB=40°,则∠OCB=____
∠OBA=____ ∠AOB=_____ ∠AOD=____
4.若已知AC=10㎝,BC=6㎝,则矩形的周长=____㎝矩形的面积=____ ㎝2
5. 若已知 ∠DOC=120°,AD=6㎝.则AC= ___ ㎝550°10100°40°12482880°练一练6.如图:在矩形ABCD中,两条对角线AC、BD相交于点O, AB=OA=4cm.
则BD=____,AD=_____
ABOCD7.如图,用8块相同的长方形地砖拼成一个矩形地面,则每块长方形地砖的长和宽分别是( )
(A)48cm,12cm; (B)48cm,16cm;
(C)44cm,16cm; (D)45cm,15cm.D(1)矩形具有而平行四边形不具有的性质( )
(A)内角和是360度(B)对角相等(C)对边平行且相等(D)对角线相等 (2)下面性质中,矩形不一定具有的是( )
(A)对角线相等(B)四个角相等(C)是轴对称图形(D)对角线垂直
(3)由已知矩形的一个顶点向其所对的对角线引垂线,该垂线分直角为3:1两部分,则垂线与另一条对角线的夹角是( )
(A)50度(B)45度(C)30度(D)22.5度
DDB课堂练习 4. 过四边形的各个顶点分别作对角线的平行线,若这四
条平行线围成一个矩形,则原四边形一定是 课堂练习A.对角线相等的四边形 B.对角线互相平分且相等的四边形
C.对角线互垂直平分的四边形 D.对角线垂直的四边形5. 已知矩形的一条对角线与一边的夹角是40°,则两
条对角线所夹锐角的度数为 A.50° B.60° C.70° D.80°6. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,
则∠BAE等于 A.30° B.45° C.60° D.120°[ ][ ][ ]DDA 学海 无涯A3.在 中,斜边AC上的中线
和高分别是6cm和5cm,则 的
面积S=( )。 A
BCDE30cm2600如图,矩形ABCD的两条对角线相交于点O,AB=4cm,∠AOB=60°,求矩形对角线的长。解:∵四边形ABCD是矩形,∴AC与BD相等且互相平分。又 ∠AOB=60°,∴ ΔOAB是等边三角形∴OA=AB=4(cm)∴ AC=BD = 2OA=2×4=8(cm)
∴ OA = OB。变式:若BD=8cm,∠AOD=120°,求边AB的长。
O1200例1:如图:在矩形ABCD中,两条对角线AC、BD相交于点O, AB=OA=4cm.
求:BD与AD的长
ABOCD例2:已知:如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AB=4cm,求矩形对角线的长.ABOCD随堂练习1. 矩形具有而一般平行四边形不具有的性质是( ).
A 对角线相等 B 对边相等
C 对角相等 D 对角线互相平分 A2.在矩形ABCD中,
AE⊥BD于E,若
BE=OE=1,则
AC= , AB=---BCDEAO423.如图,用8块相同的长方形地砖拼成一个矩形地面,则每块长方形地砖的长和宽分别是( )
(A)48cm,12cm; (B)48cm,16cm;
(C)44cm,16cm; (D)45cm,15cm.D(2).矩形的两条对角线将矩形分成四个面积
相等的等腰三角形( )(1).矩形是平行四边形( )4.矩形的短边长为3cm,两对角线所成的角是60 °,则它的另一边长是_______.5. 已知矩形对角线长为4cm,一边长为 cm,
则矩形的面积是________.6.判断题拓展与应用例. 如图,在矩形ABCD中,DE平分∠ADC交AC于E,交BC于F,若∠BDF=150,求∠COF的度数.ABOCDEF拓展与应用练习如图:在ABCD矩形中AB=6cm,BC=8cm,
将矩形折叠,
使B点与点D重合,
求折痕EF的长。ABOCDA/EF有一个角是直角的
平行四边形叫矩形2.矩形的性质:对边平行且相等四个角都是直角对角线互相平分 且相等1.矩形的定义:5.矩形是轴对称图形.3.直角三角形斜边上的中线等于斜边的一半4. 矩形的对角线把矩形分成两对全等的
等腰三角形总结矩形与平行四边形的性质对比两对角线相等且互相平分两条对角线互相平分对角线对角相等,都是90°对角相等角两组对边平行且相等两组对边平行且相等边矩形平行四边形性质2013年6月
