1.2.3 直线与平面的夹角 教学设计(表格式)
文档属性
| 名称 | 1.2.3 直线与平面的夹角 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 668.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 17:45:36 | ||
图片预览



文档简介
课程基本信息
课题 直线与平面的夹角
教科书 书名:数学 选择性必修 第一册 出版社:人民教育出版社 出版日期: 2019年 7 月
教学目标
教学目标: 理解直线与平面所成的角的概念,会作出斜线与平面所成的角; 了解直线与平面所成的角的性质,能够利用性质处理简单的线面角问题; 培养读图、作图能力,培养空间想象力。 教学重点:斜线与平面所成的角的概念与性质 教学难点:斜线与平面所成的角的概念,最小角定理
教学过程
时间 教学环节 主要师生活动
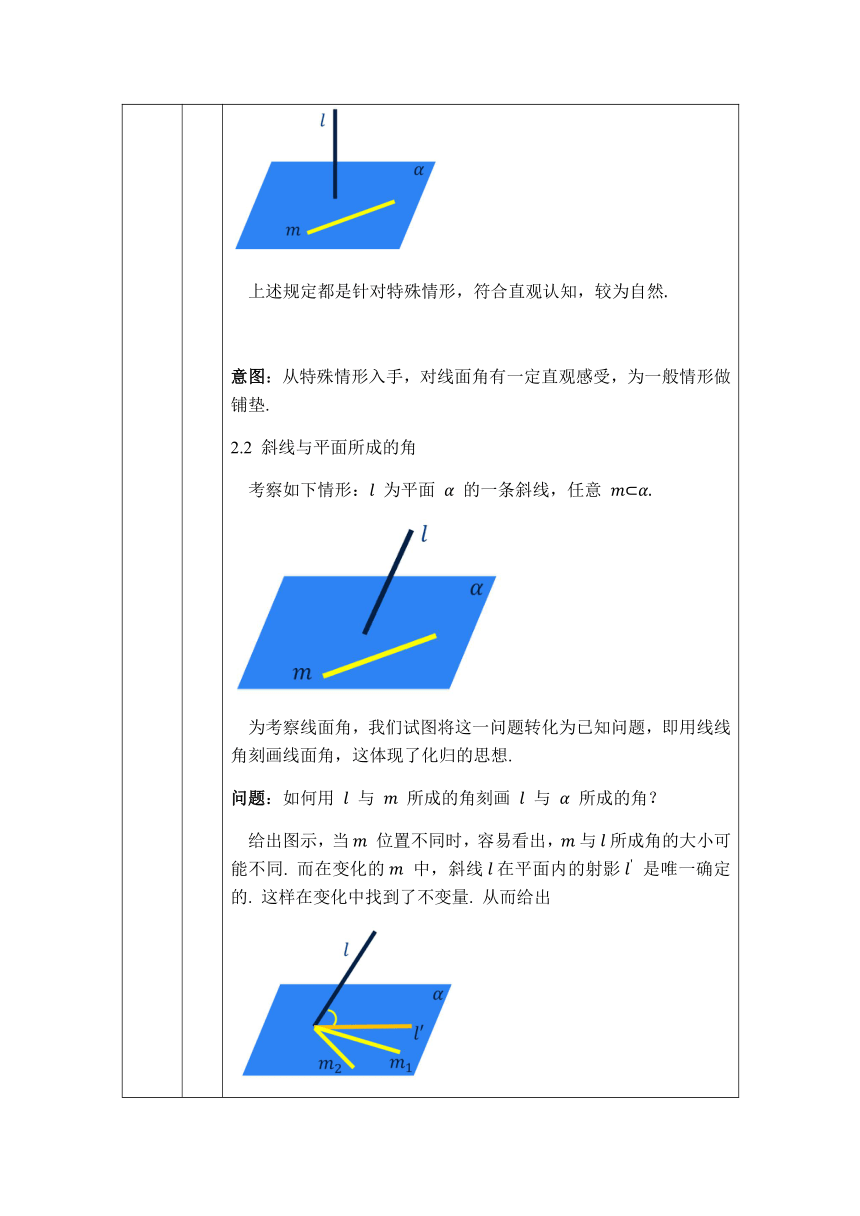
2min O. 复习回顾 I. 情境导入 O. 复习回顾 回忆:直线与平面的位置关系 根据直线与平面公共点的个数分为: 意图 为新知学习做好铺垫. I. 情境导入 日常生活中,很多情境都有直线与平面成一定角度的形象. 如握笔写字时,笔抽象成直线,纸面抽象成平面,则直线与平面成一定角度;地球仪的旋转轴与赤道所在平面垂直,与水平桌面成一定角度。 问题:如何刻画直线与平面所成的角? 意图:情境导入,引入问题、激发兴趣。
18min II. 新知 II. 新知 2.1 特殊情形的讨论 先考虑特殊情形. 当 或 ∥ 时,直观感受线面所成的角度为0°. 此时,规定: 与 所成的角为 0°. 当 时,我们知道,对任意,都有. 此时,规定: 与 所成的角为 90°. 上述规定都是针对特殊情形,符合直观认知,较为自然. 意图:从特殊情形入手,对线面角有一定直观感受,为一般情形做铺垫. 2.2 斜线与平面所成的角 考察如下情形: 为平面 的一条斜线,任意 . 为考察线面角,我们试图将这一问题转化为已知问题,即用线线角刻画线面角,这体现了化归的思想. 问题:如何用 与 所成的角刻画 与 所成的角? 给出图示,当 位置不同时,容易看出,与所成角的大小可能不同. 而在变化的 中,斜线在平面内的射影 是唯一确定的. 这样在变化中找到了不变量. 从而给出 定义:平面的斜线与它在平面内的射影所成的锐角,称为这条斜线与平面所成的角. 结合图示,进一步解释: 思考 线面角的取值范围. 设 是直线与平面所成的角(也称为直线与平面的夹角),则 0°≤ ≤90°. 意图:化归思想的体现;变化中寻找不变量;自然语言、图形语言与符号语言的统一. 2.3 例 正方体 ′ ′ ′ ′ 中,分析 (1) 体对角线 ′ 与底面 所成的角; (2) 体对角线与侧面所成的角. 分析 进一步求得, 意图:通过作图,加深对概念的理解. 2.4 直线与平面所成角的性质 性质1 射影长度与斜线段长度 线段 所在直线与 所成的角为 , 在平面 内的射影为 ′ ′. 则,射影长度 ′ ′= cos . 这条性质揭示了斜线段长度、射影长度、斜线段所在直线与平面夹角三者之间的数量关系. 例 设线段在平面内的射影为,直线与的夹角为. 分析 直接利用性质1,结合图示分析: 性质2 最小角定理 如图,斜线段 ∩ = , ′ 为 在 内的射影, , ′ ⊥ 于 . 记. 探索 之间的等量关系. 分析 借助三角函数寻求角度之间的关系. 因,故为直角三角形,且为在内的射影. 又,结合三垂线定理,有, 故为直角三角形. 设. 中,, 中,, 中,. 因此 . 这条性质说明:平面的斜线与平面所成的角,是斜线和这个平面内所有直线所成角中最小的角. 例 在平面内.过引的斜线,使, 为在内的射影. 求证:平分. 分析 结论的意义: 斜线和角的两边所成的角相等,从而射影和角的两边所成的角相等. 欲证角度相等,去寻求角度的三角函数值的等量关系. 利用性质2. 解答 根据性质2, 性质3 为平面外一点,在内的射影为. 过作的斜线段,斜足为. 设与所成角分别为. 则根据三角形全等容易得到: 这条性质说明:经过平面外一点所作的平面的多条斜线中,斜线段长、射影长、斜线与平面所成的角,三者其一相等,另外两个也相等. 意图:通过性质的刻画,进一步深化线面角的概念,加强理解.
2min III. 小结 III. 小结 基本想法:利用线线角刻画线面角 基本思路: 找射影——依靠垂直关系 定夹角——平面角 性质: 把握斜线、射影、线面角之间的关系
作业 教材 46页 A组 1,2,B组 2;59页 A组 6
课题 直线与平面的夹角
教科书 书名:数学 选择性必修 第一册 出版社:人民教育出版社 出版日期: 2019年 7 月
教学目标
教学目标: 理解直线与平面所成的角的概念,会作出斜线与平面所成的角; 了解直线与平面所成的角的性质,能够利用性质处理简单的线面角问题; 培养读图、作图能力,培养空间想象力。 教学重点:斜线与平面所成的角的概念与性质 教学难点:斜线与平面所成的角的概念,最小角定理
教学过程
时间 教学环节 主要师生活动
2min O. 复习回顾 I. 情境导入 O. 复习回顾 回忆:直线与平面的位置关系 根据直线与平面公共点的个数分为: 意图 为新知学习做好铺垫. I. 情境导入 日常生活中,很多情境都有直线与平面成一定角度的形象. 如握笔写字时,笔抽象成直线,纸面抽象成平面,则直线与平面成一定角度;地球仪的旋转轴与赤道所在平面垂直,与水平桌面成一定角度。 问题:如何刻画直线与平面所成的角? 意图:情境导入,引入问题、激发兴趣。
18min II. 新知 II. 新知 2.1 特殊情形的讨论 先考虑特殊情形. 当 或 ∥ 时,直观感受线面所成的角度为0°. 此时,规定: 与 所成的角为 0°. 当 时,我们知道,对任意,都有. 此时,规定: 与 所成的角为 90°. 上述规定都是针对特殊情形,符合直观认知,较为自然. 意图:从特殊情形入手,对线面角有一定直观感受,为一般情形做铺垫. 2.2 斜线与平面所成的角 考察如下情形: 为平面 的一条斜线,任意 . 为考察线面角,我们试图将这一问题转化为已知问题,即用线线角刻画线面角,这体现了化归的思想. 问题:如何用 与 所成的角刻画 与 所成的角? 给出图示,当 位置不同时,容易看出,与所成角的大小可能不同. 而在变化的 中,斜线在平面内的射影 是唯一确定的. 这样在变化中找到了不变量. 从而给出 定义:平面的斜线与它在平面内的射影所成的锐角,称为这条斜线与平面所成的角. 结合图示,进一步解释: 思考 线面角的取值范围. 设 是直线与平面所成的角(也称为直线与平面的夹角),则 0°≤ ≤90°. 意图:化归思想的体现;变化中寻找不变量;自然语言、图形语言与符号语言的统一. 2.3 例 正方体 ′ ′ ′ ′ 中,分析 (1) 体对角线 ′ 与底面 所成的角; (2) 体对角线与侧面所成的角. 分析 进一步求得, 意图:通过作图,加深对概念的理解. 2.4 直线与平面所成角的性质 性质1 射影长度与斜线段长度 线段 所在直线与 所成的角为 , 在平面 内的射影为 ′ ′. 则,射影长度 ′ ′= cos . 这条性质揭示了斜线段长度、射影长度、斜线段所在直线与平面夹角三者之间的数量关系. 例 设线段在平面内的射影为,直线与的夹角为. 分析 直接利用性质1,结合图示分析: 性质2 最小角定理 如图,斜线段 ∩ = , ′ 为 在 内的射影, , ′ ⊥ 于 . 记. 探索 之间的等量关系. 分析 借助三角函数寻求角度之间的关系. 因,故为直角三角形,且为在内的射影. 又,结合三垂线定理,有, 故为直角三角形. 设. 中,, 中,, 中,. 因此 . 这条性质说明:平面的斜线与平面所成的角,是斜线和这个平面内所有直线所成角中最小的角. 例 在平面内.过引的斜线,使, 为在内的射影. 求证:平分. 分析 结论的意义: 斜线和角的两边所成的角相等,从而射影和角的两边所成的角相等. 欲证角度相等,去寻求角度的三角函数值的等量关系. 利用性质2. 解答 根据性质2, 性质3 为平面外一点,在内的射影为. 过作的斜线段,斜足为. 设与所成角分别为. 则根据三角形全等容易得到: 这条性质说明:经过平面外一点所作的平面的多条斜线中,斜线段长、射影长、斜线与平面所成的角,三者其一相等,另外两个也相等. 意图:通过性质的刻画,进一步深化线面角的概念,加强理解.
2min III. 小结 III. 小结 基本想法:利用线线角刻画线面角 基本思路: 找射影——依靠垂直关系 定夹角——平面角 性质: 把握斜线、射影、线面角之间的关系
作业 教材 46页 A组 1,2,B组 2;59页 A组 6
