2.5 椭圆及其方程小结 教学设计(表格式)
文档属性
| 名称 | 2.5 椭圆及其方程小结 教学设计(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 134.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 17:45:36 | ||
图片预览

文档简介
课程基本信息
课题 2.5 椭圆及其方程小结
教科书 书名: 《普通高中教科书·数学(B版)·选择性必修·第一册》 出版社:人民教育出版社 出版日期: 2020 年 6 月
教学目标
教学目标:进一步巩固椭圆的定义和标准方程,熟练椭圆的几何性质,在此基础上,根据题目条件合理地选择椭圆定义和标准方程去解决有关问题. 教学重点:椭圆上点的几何特征和代数特征以及这些特征的应用. 教学难点:椭圆上点的几何特征和代数特征的合理应用.
教学过程
时间 教学环节 主要师生活动
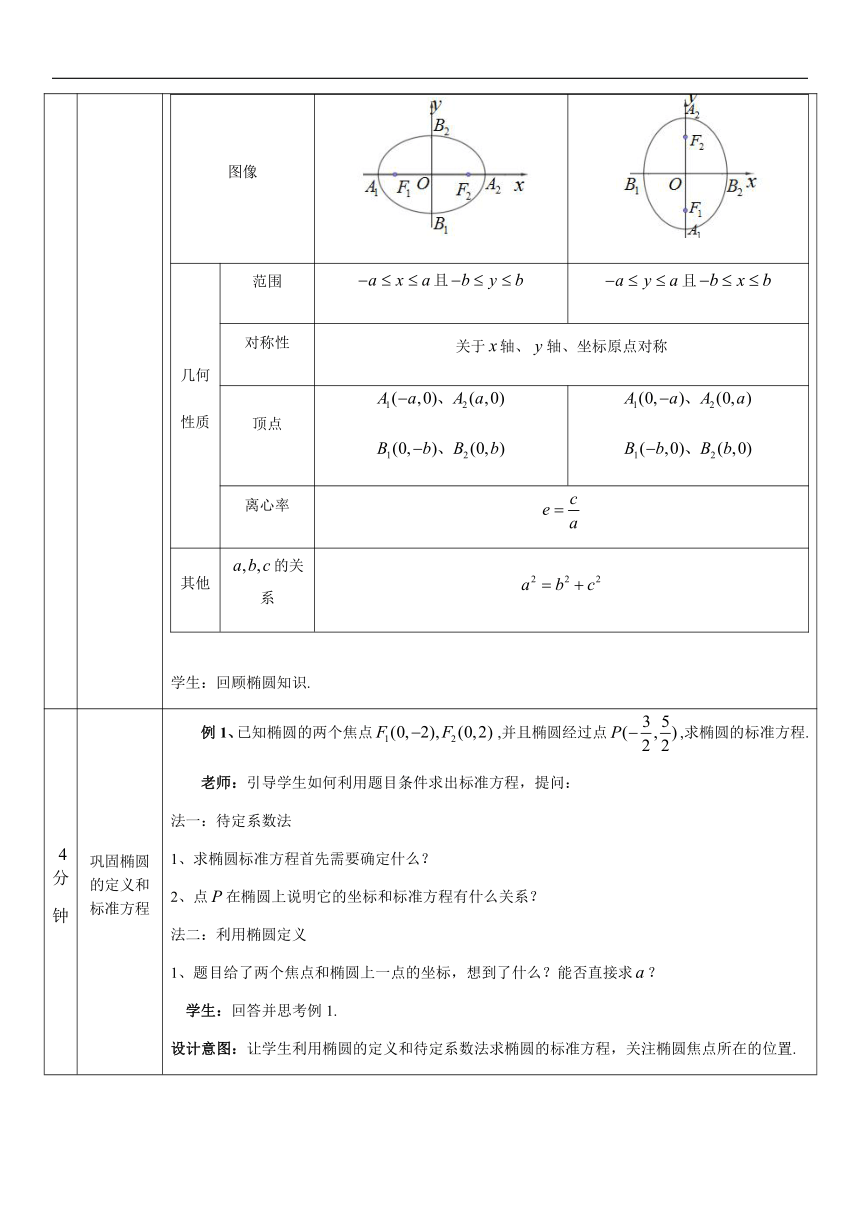
2 分 钟 梳理椭圆知识 老师:梳理椭圆的知识,强调椭圆定义和标准方程中要注意的点,如下表: 名称椭圆定义如果是平面内的两个定点,是一个常数,且,则平面内满足的动点的轨迹称为椭圆。焦点标准方程图像几何性质范围且且对称性关于轴、轴、坐标原点对称顶点 离心率其他的关系
学生:回顾椭圆知识.
4分 钟 巩固椭圆的定义和标准方程 例1、已知椭圆的两个焦点,并且椭圆经过点,求椭圆的标准方程. 老师:引导学生如何利用题目条件求出标准方程,提问: 法一:待定系数法 求椭圆标准方程首先需要确定什么? 点在椭圆上说明它的坐标和标准方程有什么关系? 法二:利用椭圆定义 1、题目给了两个焦点和椭圆上一点的坐标,想到了什么?能否直接求? 学生:回答并思考例1. 设计意图:让学生利用椭圆的定义和待定系数法求椭圆的标准方程,关注椭圆焦点所在的位置.
9分 钟 提炼解决椭圆有关问题的一般方法 活动1、体会椭圆上的点的几何特征和代数特征. 例2、已知椭圆的两个焦点,过点且与坐标轴不平行的直线与椭圆相交于两点,如果的周长等于12,求这个椭圆的标准方程. 老师:引导学生如何利用题目周长条件求出标准方程,提问: 在周长公式中出现了和这两个量,想到了什么? 两点在椭圆上说明什么? 学生:回答并思考例2. 设计意图:让学生分析题目条件利用椭圆的定义去求椭圆的标准方程. 例3、已知椭圆上一点与两个焦点的连线互相垂直,求的面积. 老师:讲解例3,引导学生尝试用椭圆的定义和标准方程两个角度去思考问题,总结一般方法.提问: 法一:设点坐标利用椭圆的标准方程 公式中,我们要想得到点的坐标,但又无法直接求,我们可以先怎么做? 设点的坐标为,怎样利用坐标刻画? 除了利用向量刻画,还可以转化为什么? 法二:利用椭圆的定义 面积公式我们自然想到,那之间有什么关系? 说明之间有什么关系? 学生:回答并思考例3. 设计意图:让学生利用椭圆的定义和标准方程解决问题,体会椭圆上的点的几何特征和代数特征. 活动2、总结刻画点在椭圆上的两种方法. 老师提问:点在椭圆上可以从哪两个角度刻画? 设计意图:让学生总结解决椭圆有关问题的一般方法.
8分 钟 辨析方法 活动1、利用椭圆上的点的代数特征解决问题. 例4、已知点是椭圆的长轴的左端点,以点为直角顶点作一个内接于椭圆的等腰直角三角形,求斜边的长. 老师:讲解例4,引导学生用椭圆上的点的代数特征来解决问题.提问: 利用等腰直角三角形这个条件如何求斜边的长,和什么有关? 怎样用坐标刻画为等腰直角三角形? 例4可以用椭圆的定义解决吗?为什么不行? 学生:回答并思考例4. 活动2、利用椭圆上的点的几何特征解决问题. 例5、过椭圆的左焦点作轴的垂线交椭圆于点,为右焦点,若,求椭圆的离心率. 老师:讲解例5,引导学生用椭圆上的点的几何特征来解决问题.提问: 1、是边和边的夹角,涉及到、这两个量,这两个量有什么关系? 2、由对称性可知直线垂直于轴,说明点和点的横坐标一样,如果我们设点的坐标为,点的坐标是什么?点在椭圆上说明什么? 3、对比此题的两种方法,此题你觉得哪种方法好?什么情况下我们优先考虑椭圆的定义? 学生:回答并思考例5,体会当题目涉及椭圆上一点到两焦点的距离时,我们优先考虑椭圆的定义. 设计意图:通过对比例4和例5的解决方法,让学生进一步思考如何合理选用椭圆的定义和标准方法解决问题?
1分 钟 课堂总结 活动:老师引导学生总结点在椭圆上可以从点的几何特征和代数特征两个角度思考问题,并引导学生比较两种方法.
课题 2.5 椭圆及其方程小结
教科书 书名: 《普通高中教科书·数学(B版)·选择性必修·第一册》 出版社:人民教育出版社 出版日期: 2020 年 6 月
教学目标
教学目标:进一步巩固椭圆的定义和标准方程,熟练椭圆的几何性质,在此基础上,根据题目条件合理地选择椭圆定义和标准方程去解决有关问题. 教学重点:椭圆上点的几何特征和代数特征以及这些特征的应用. 教学难点:椭圆上点的几何特征和代数特征的合理应用.
教学过程
时间 教学环节 主要师生活动
2 分 钟 梳理椭圆知识 老师:梳理椭圆的知识,强调椭圆定义和标准方程中要注意的点,如下表: 名称椭圆定义如果是平面内的两个定点,是一个常数,且,则平面内满足的动点的轨迹称为椭圆。焦点标准方程图像几何性质范围且且对称性关于轴、轴、坐标原点对称顶点 离心率其他的关系
学生:回顾椭圆知识.
4分 钟 巩固椭圆的定义和标准方程 例1、已知椭圆的两个焦点,并且椭圆经过点,求椭圆的标准方程. 老师:引导学生如何利用题目条件求出标准方程,提问: 法一:待定系数法 求椭圆标准方程首先需要确定什么? 点在椭圆上说明它的坐标和标准方程有什么关系? 法二:利用椭圆定义 1、题目给了两个焦点和椭圆上一点的坐标,想到了什么?能否直接求? 学生:回答并思考例1. 设计意图:让学生利用椭圆的定义和待定系数法求椭圆的标准方程,关注椭圆焦点所在的位置.
9分 钟 提炼解决椭圆有关问题的一般方法 活动1、体会椭圆上的点的几何特征和代数特征. 例2、已知椭圆的两个焦点,过点且与坐标轴不平行的直线与椭圆相交于两点,如果的周长等于12,求这个椭圆的标准方程. 老师:引导学生如何利用题目周长条件求出标准方程,提问: 在周长公式中出现了和这两个量,想到了什么? 两点在椭圆上说明什么? 学生:回答并思考例2. 设计意图:让学生分析题目条件利用椭圆的定义去求椭圆的标准方程. 例3、已知椭圆上一点与两个焦点的连线互相垂直,求的面积. 老师:讲解例3,引导学生尝试用椭圆的定义和标准方程两个角度去思考问题,总结一般方法.提问: 法一:设点坐标利用椭圆的标准方程 公式中,我们要想得到点的坐标,但又无法直接求,我们可以先怎么做? 设点的坐标为,怎样利用坐标刻画? 除了利用向量刻画,还可以转化为什么? 法二:利用椭圆的定义 面积公式我们自然想到,那之间有什么关系? 说明之间有什么关系? 学生:回答并思考例3. 设计意图:让学生利用椭圆的定义和标准方程解决问题,体会椭圆上的点的几何特征和代数特征. 活动2、总结刻画点在椭圆上的两种方法. 老师提问:点在椭圆上可以从哪两个角度刻画? 设计意图:让学生总结解决椭圆有关问题的一般方法.
8分 钟 辨析方法 活动1、利用椭圆上的点的代数特征解决问题. 例4、已知点是椭圆的长轴的左端点,以点为直角顶点作一个内接于椭圆的等腰直角三角形,求斜边的长. 老师:讲解例4,引导学生用椭圆上的点的代数特征来解决问题.提问: 利用等腰直角三角形这个条件如何求斜边的长,和什么有关? 怎样用坐标刻画为等腰直角三角形? 例4可以用椭圆的定义解决吗?为什么不行? 学生:回答并思考例4. 活动2、利用椭圆上的点的几何特征解决问题. 例5、过椭圆的左焦点作轴的垂线交椭圆于点,为右焦点,若,求椭圆的离心率. 老师:讲解例5,引导学生用椭圆上的点的几何特征来解决问题.提问: 1、是边和边的夹角,涉及到、这两个量,这两个量有什么关系? 2、由对称性可知直线垂直于轴,说明点和点的横坐标一样,如果我们设点的坐标为,点的坐标是什么?点在椭圆上说明什么? 3、对比此题的两种方法,此题你觉得哪种方法好?什么情况下我们优先考虑椭圆的定义? 学生:回答并思考例5,体会当题目涉及椭圆上一点到两焦点的距离时,我们优先考虑椭圆的定义. 设计意图:通过对比例4和例5的解决方法,让学生进一步思考如何合理选用椭圆的定义和标准方法解决问题?
1分 钟 课堂总结 活动:老师引导学生总结点在椭圆上可以从点的几何特征和代数特征两个角度思考问题,并引导学生比较两种方法.
