2.6 双曲线及其方程小结 教学设计(表格式)
文档属性
| 名称 | 2.6 双曲线及其方程小结 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 27.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 17:45:36 | ||
图片预览



文档简介
课程基本信息
课题 双曲线及其方程小结
教科书 书名:普通高中教科书数学选择性必修第一册(B版) 出版社:人民教育出版社 出版日期:2020年 6月
教学目标
教学目标: 会求双曲线的标准方程,能关注到焦点位置; 能正确处理有关离心率和渐近线的问题. 教学重点:正确处理双曲线标准方程、离心率等问题. 教学难点:涉及渐近线的处理.
教学过程
时间 教学环节 主要师生活动
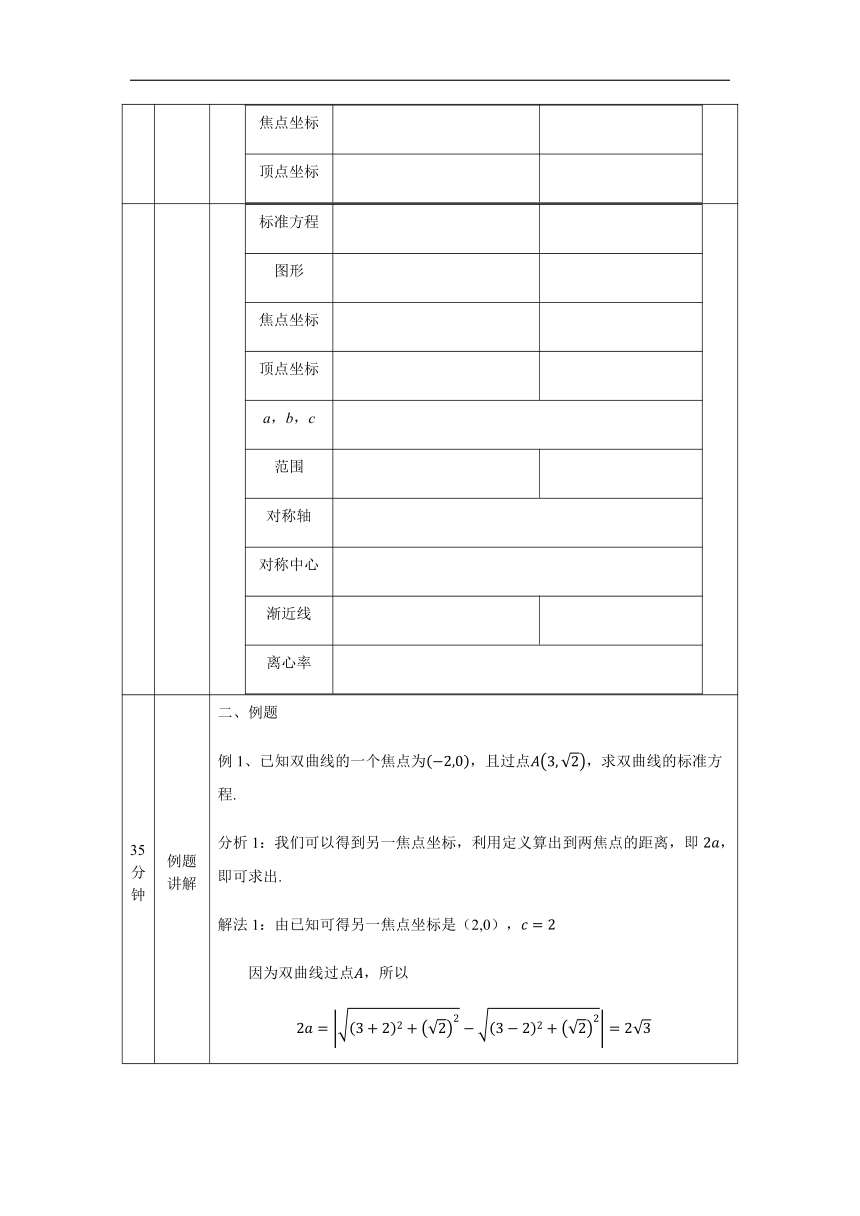
3分钟 复习回顾 一、复习回顾 1、双曲线的定义 F1,F2是平面内的两个定点,a是一个正常数,且2a<|F1F2|,则平面上满足| |PF1|-|PF2 | |=2a的动点P的轨迹称为双曲线. 2、双曲线的方程、图形和性质 请完成下列表格: 标准方程图形焦点坐标顶点坐标
标准方程图形焦点坐标顶点坐标a,b,c范围对称轴对称中心渐近线离心率
35分钟 例题讲解 二、例题 例1、已知双曲线的一个焦点为,且过点,求双曲线的标准方程. 分析1:我们可以得到另一焦点坐标,利用定义算出到两焦点的距离,即,即可求出. 解法1:由已知可得另一焦点坐标是(2,0), 因为双曲线过点,所以 所以, 又因为焦点在轴上,所以所求双曲线方程为: 分析2:我们还可以设出方程,将,代入点坐标即可,这是待定系数法. 解法2:由已知可得,所以,且焦点在轴上,所以设所求双曲线方程为: 因为双曲线过点,所以
解得:, 所求双曲线方程为: 例2、已知双曲线经过点,,求双曲线的标准方程. 分析1:不能直接得到a,b,c,的值,考虑用待定系数法设出双曲线的方程,但是焦点在什么位置,该用哪个标准方程呢?可以讨论试试. 解法1:当焦点在x轴上时,设双曲线方程为: 因为双曲线经过点,,所以 解得 ,舍去; 所以焦点在x轴的情况不存在. 当焦点在y轴上时,设双曲线方程为: 因为双曲线经过点,,所以 解得 , 所求双曲线方程为: 分析2:其实这两个方程:和从方程形式来看其实是一样的,都可以用:m,椭圆标准方程也是这样的,再代入点的坐标,求出即可. 解:设双曲线的方程为:,因为双曲线经过点,,所以 解得:, 所求双曲线方程为: 另外:还可以利用对称性,把M,N关于x轴、y轴、原点对称,把两点变成八个点,在坐标系中描出来,也能判断焦点位置,课后可以试试. 例3、已知双曲线的一条渐近线方程为,且双曲线过点,求双曲线的标准方程. 分析1:渐近线方程写成,但是还是,还需要判断焦点在x轴还是y轴上,因为有渐近线,可以画图试试,可以计算当时,对应的渐近线上的点的纵坐标比4大还是比4小,判断A点在渐近线的哪个区域中,从而判断焦点的位置. 解法1:当时,,所以可以判断点A在两条渐近线相交所成的四个区域中的右边区域里,所以焦点在x轴上,所以有,设a=2k,b=3k,k>0, 则设所求双曲线方程为:因为双曲线过点所以有 解得:,所以所求双曲线的方程为: 分析2:我们来看看渐近线方程和双曲线方程之间的关系. 对于焦点在x轴上的情况: 我们将这两个式子相乘的话那就是: 和双曲线方程比差别就是等式右边1变成0,也就是只需将双曲线方程右边1变成0,就可得到渐近线方程. 通过举例让学生来体会: 再到:. 明白对于方程为:的一类双曲线,其渐近线方程是相同的,都是,反之,如果知道渐近线方程为:,那就可以设双曲线方程为:,再加一个条件就能求出双曲线方程了. 解法2:由题可知,设双曲线方程为: 因为点在双曲线上,所以有 所以 所以所求双曲线的方程为: 例4、已知双曲线的顶点为,虚轴的一个端点为,且是一个等边三角形,求双曲线的离心率. 分析:离心率是比值,需要得到a,b,c的关系式来导出比值. 画图试试就能得到关系式了. 解:作于,则, 因为是等边三角形,所以 所以 所以,从而 例5、已知双曲线的渐近线方程为:,求双曲线的离心率. 分析:渐近线的斜率是a和b的比值,因此可以得到c与a的比值,但是双曲线焦点位置不确定,因此和都有可能. 解:当双曲线焦点在x轴上时,有,设a=4m,b=3m,m>0, 可得c=5m,所以 当双曲线焦点在y轴上时,有,设a=3m,b=4m,m>0, 可得c=5m,所以 综上,离心率为或 .
课 堂 小 结 处理双曲线问题时,注意以下几点: 1、如果涉及到双曲线两焦点距离时,可以考虑双曲线的定义; 2、要注意焦点的位置带来的影响; 3、求双曲线的标准方程时,要注意待定系数法的使用; 4、离心率是比值,求离心率时注意得到关于a,b,c的关系式; 5、已知双曲线的渐近线方程,可以使用来求解.
布 置 作 业 课本第149页,习题2-6A组第4题,B组第2题,第5题 A4:已知中心在原点的双曲线的一个焦点是F1,一条渐 近线方程是,求此双曲线的标准方程. B2:已知P是双曲线上一点,求的最小值. B5:已知F1,F2是双曲线的两个焦点,点M在双曲线上,如果 MF1⊥MF2,求△MF1F2的面积.
课题 双曲线及其方程小结
教科书 书名:普通高中教科书数学选择性必修第一册(B版) 出版社:人民教育出版社 出版日期:2020年 6月
教学目标
教学目标: 会求双曲线的标准方程,能关注到焦点位置; 能正确处理有关离心率和渐近线的问题. 教学重点:正确处理双曲线标准方程、离心率等问题. 教学难点:涉及渐近线的处理.
教学过程
时间 教学环节 主要师生活动
3分钟 复习回顾 一、复习回顾 1、双曲线的定义 F1,F2是平面内的两个定点,a是一个正常数,且2a<|F1F2|,则平面上满足| |PF1|-|PF2 | |=2a的动点P的轨迹称为双曲线. 2、双曲线的方程、图形和性质 请完成下列表格: 标准方程图形焦点坐标顶点坐标
标准方程图形焦点坐标顶点坐标a,b,c范围对称轴对称中心渐近线离心率
35分钟 例题讲解 二、例题 例1、已知双曲线的一个焦点为,且过点,求双曲线的标准方程. 分析1:我们可以得到另一焦点坐标,利用定义算出到两焦点的距离,即,即可求出. 解法1:由已知可得另一焦点坐标是(2,0), 因为双曲线过点,所以 所以, 又因为焦点在轴上,所以所求双曲线方程为: 分析2:我们还可以设出方程,将,代入点坐标即可,这是待定系数法. 解法2:由已知可得,所以,且焦点在轴上,所以设所求双曲线方程为: 因为双曲线过点,所以
解得:, 所求双曲线方程为: 例2、已知双曲线经过点,,求双曲线的标准方程. 分析1:不能直接得到a,b,c,的值,考虑用待定系数法设出双曲线的方程,但是焦点在什么位置,该用哪个标准方程呢?可以讨论试试. 解法1:当焦点在x轴上时,设双曲线方程为: 因为双曲线经过点,,所以 解得 ,舍去; 所以焦点在x轴的情况不存在. 当焦点在y轴上时,设双曲线方程为: 因为双曲线经过点,,所以 解得 , 所求双曲线方程为: 分析2:其实这两个方程:和从方程形式来看其实是一样的,都可以用:m,椭圆标准方程也是这样的,再代入点的坐标,求出即可. 解:设双曲线的方程为:,因为双曲线经过点,,所以 解得:, 所求双曲线方程为: 另外:还可以利用对称性,把M,N关于x轴、y轴、原点对称,把两点变成八个点,在坐标系中描出来,也能判断焦点位置,课后可以试试. 例3、已知双曲线的一条渐近线方程为,且双曲线过点,求双曲线的标准方程. 分析1:渐近线方程写成,但是还是,还需要判断焦点在x轴还是y轴上,因为有渐近线,可以画图试试,可以计算当时,对应的渐近线上的点的纵坐标比4大还是比4小,判断A点在渐近线的哪个区域中,从而判断焦点的位置. 解法1:当时,,所以可以判断点A在两条渐近线相交所成的四个区域中的右边区域里,所以焦点在x轴上,所以有,设a=2k,b=3k,k>0, 则设所求双曲线方程为:因为双曲线过点所以有 解得:,所以所求双曲线的方程为: 分析2:我们来看看渐近线方程和双曲线方程之间的关系. 对于焦点在x轴上的情况: 我们将这两个式子相乘的话那就是: 和双曲线方程比差别就是等式右边1变成0,也就是只需将双曲线方程右边1变成0,就可得到渐近线方程. 通过举例让学生来体会: 再到:. 明白对于方程为:的一类双曲线,其渐近线方程是相同的,都是,反之,如果知道渐近线方程为:,那就可以设双曲线方程为:,再加一个条件就能求出双曲线方程了. 解法2:由题可知,设双曲线方程为: 因为点在双曲线上,所以有 所以 所以所求双曲线的方程为: 例4、已知双曲线的顶点为,虚轴的一个端点为,且是一个等边三角形,求双曲线的离心率. 分析:离心率是比值,需要得到a,b,c的关系式来导出比值. 画图试试就能得到关系式了. 解:作于,则, 因为是等边三角形,所以 所以 所以,从而 例5、已知双曲线的渐近线方程为:,求双曲线的离心率. 分析:渐近线的斜率是a和b的比值,因此可以得到c与a的比值,但是双曲线焦点位置不确定,因此和都有可能. 解:当双曲线焦点在x轴上时,有,设a=4m,b=3m,m>0, 可得c=5m,所以 当双曲线焦点在y轴上时,有,设a=3m,b=4m,m>0, 可得c=5m,所以 综上,离心率为或 .
课 堂 小 结 处理双曲线问题时,注意以下几点: 1、如果涉及到双曲线两焦点距离时,可以考虑双曲线的定义; 2、要注意焦点的位置带来的影响; 3、求双曲线的标准方程时,要注意待定系数法的使用; 4、离心率是比值,求离心率时注意得到关于a,b,c的关系式; 5、已知双曲线的渐近线方程,可以使用来求解.
布 置 作 业 课本第149页,习题2-6A组第4题,B组第2题,第5题 A4:已知中心在原点的双曲线的一个焦点是F1,一条渐 近线方程是,求此双曲线的标准方程. B2:已知P是双曲线上一点,求的最小值. B5:已知F1,F2是双曲线的两个焦点,点M在双曲线上,如果 MF1⊥MF2,求△MF1F2的面积.
