2.6.2 双曲线的几何性质 教学设计(表格式)
文档属性
| 名称 | 2.6.2 双曲线的几何性质 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 310.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 00:00:00 | ||
图片预览


文档简介
课程基本信息
课题 双曲线的几何性质
教科书 书名:普通高中教科书数学选择性必修第一册(B版) 出版社:人民教育出版社 出版日期:2020年 6月
教学目标
教学目标: 1、能运用双曲线的标准方程讨论双曲线的范围、对称性、顶点、离心率、渐近线等几何性质,并掌握这些几何性质,理解双曲线的离心率的含义,从几何和代数两个角度来理解双曲线的渐近线; 2、进一步理解利用方程研究曲线性质的思想和方法. 教学重点: 1、双曲线的几何性质及简单应用. 2、进一步理解、运用和感悟从代数角度研究几何的思想和方法. 教学难点:双曲线的渐近线的发现、认识和从几何代数两个角度理解.
教学过程
时间 教学环节 主要师生活动
3分钟 复 习 回 顾 1、回顾椭圆性质的学习过程,回答以下两个问题: 问题1:我们是借助什么来研究椭圆的几何性质的? 答:借助椭圆的标准方程. 问题2:从哪些方面研究了椭圆的几何性质? 答:范围、对称性、顶点、离心率等. 2、回顾上节课的内容,回答问题: 问题3: 双曲线的标准方程是什么? 答:焦点在轴上的双曲线的标准方程是: 焦点在轴上的双曲线的标准方程:
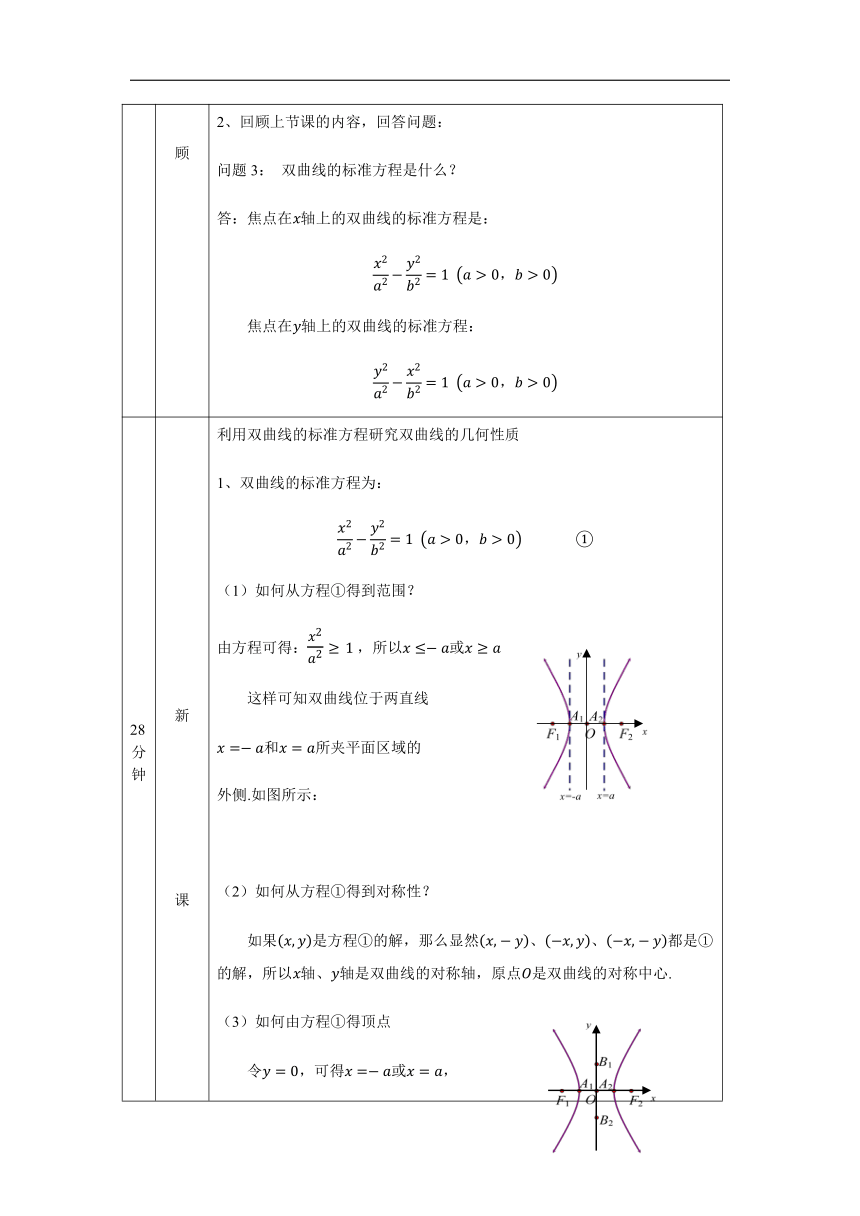
28分钟 新 课 利用双曲线的标准方程研究双曲线的几何性质 1、双曲线的标准方程为: (1)如何从方程①得到范围? 由方程可得:,所以 这样可知双曲线位于两直线 所夹平面区域的 外侧.如图所示: (2)如何从方程①得到对称性? 如果是方程①的解,那么显然都是①的解,所以轴、轴是双曲线的对称轴,原点是双曲线的对称中心. (3)如何由方程①得顶点 令,可得, 而令,方程无解,所以双曲线 与轴有两交点、, 与轴无交点. 、就是双曲线顶点,线段称为双曲线的实轴. 记,称线段为双曲线的虚轴. 等轴双曲线:实轴长等于虚轴长 (4)渐近线 观察双曲线上一点的横纵坐标的变化情况: 当增大时,也增大 根据对称性,先考虑第一象限情况: 将方程①改写成:这样便于考察y随x的变化是如何变化的. 当时, 从图形看,双曲线始终在直线下方,不会与之相交 而且,当越来越大时: 这样点越来越接近直线. 因此,从几何直观看,双曲线在第一象限随着x的增加,越来越接近直线但又始终不相交.根据对称性,在其他几个象限也是这样的,双曲线在四个方向上越来越接近这两条直线,但不会与这条直线相交. 换个角度来看上述情形,仍以第一象限为例, 计算点到直线(即)的距离,当时,,但d≠0 当时,,所以在第一象限内,随着的增大点会越来越接近直线,但不会与这条直线相交. 直线称之为该双曲线的渐近线. 问题4:如何才能把双曲线的图像画得比较好点? 先画出矩形和渐近线,再来画双曲线. 5、离心率 同椭圆一样,定义双曲线的半焦距与半实轴之比为离心率,即: 问题5:的范围是什么? 答: 问题6:逐渐增大时,双曲线会怎么变化? 答:开口越来越大. 先通过3个具体例子比较来看: 然后分析渐近线的斜率的绝对值: e 越趋近于1 ,则 越小,双曲线的渐近线所夹的双曲线区域越狭窄; e 越来越大时,则 越大,双曲线的渐近线所夹的双曲线区域越开阔. 2、双曲线的标准方程为: 请大家类比椭圆写出方程②,即焦点在轴上的双曲线的几何性质: (1)范围: (2)对称性: 对称轴:轴和轴 对称中心:原点 (3)顶点坐标: 实轴:线段 虚轴:线段 (4)渐近线方程: (5)离心率:
6分钟 例 题 例 求下列方程表示的双曲线的实轴长、焦点坐标、离心率及渐近线方程. 解:(1)由方程可知,焦点在轴上,且, 所以 所以实轴长,焦点坐标为: 离心率: 渐近线方程为: (2)将双曲线方程化成标准方程形式: 可知焦点在轴上,且, 所以,即 所以实轴长,焦点坐标为: 离心率: 渐近线方程为:
2分钟 课 堂 小 结 1、利用双曲线的标准方程来研究双曲线的几何性质,再次体会用代数方程研究曲线性质的思想和方法; 2、双曲线的几何性质和椭圆类似,注意它们的不同,尤其要重视对渐近线的认识,要从几何和代数两个角度加以理解; 3、在具体表示几何性质时,要区分焦点在x轴或y轴.
1分钟 课 后 作 业 课本P148,练习A第1题,练习B第1题. A1:写出的实轴长、虚轴长、焦点坐标、渐近线方程. B1:求双曲线实轴长、虚轴长、焦点坐标、离心率及渐近线方程.
课题 双曲线的几何性质
教科书 书名:普通高中教科书数学选择性必修第一册(B版) 出版社:人民教育出版社 出版日期:2020年 6月
教学目标
教学目标: 1、能运用双曲线的标准方程讨论双曲线的范围、对称性、顶点、离心率、渐近线等几何性质,并掌握这些几何性质,理解双曲线的离心率的含义,从几何和代数两个角度来理解双曲线的渐近线; 2、进一步理解利用方程研究曲线性质的思想和方法. 教学重点: 1、双曲线的几何性质及简单应用. 2、进一步理解、运用和感悟从代数角度研究几何的思想和方法. 教学难点:双曲线的渐近线的发现、认识和从几何代数两个角度理解.
教学过程
时间 教学环节 主要师生活动
3分钟 复 习 回 顾 1、回顾椭圆性质的学习过程,回答以下两个问题: 问题1:我们是借助什么来研究椭圆的几何性质的? 答:借助椭圆的标准方程. 问题2:从哪些方面研究了椭圆的几何性质? 答:范围、对称性、顶点、离心率等. 2、回顾上节课的内容,回答问题: 问题3: 双曲线的标准方程是什么? 答:焦点在轴上的双曲线的标准方程是: 焦点在轴上的双曲线的标准方程:
28分钟 新 课 利用双曲线的标准方程研究双曲线的几何性质 1、双曲线的标准方程为: (1)如何从方程①得到范围? 由方程可得:,所以 这样可知双曲线位于两直线 所夹平面区域的 外侧.如图所示: (2)如何从方程①得到对称性? 如果是方程①的解,那么显然都是①的解,所以轴、轴是双曲线的对称轴,原点是双曲线的对称中心. (3)如何由方程①得顶点 令,可得, 而令,方程无解,所以双曲线 与轴有两交点、, 与轴无交点. 、就是双曲线顶点,线段称为双曲线的实轴. 记,称线段为双曲线的虚轴. 等轴双曲线:实轴长等于虚轴长 (4)渐近线 观察双曲线上一点的横纵坐标的变化情况: 当增大时,也增大 根据对称性,先考虑第一象限情况: 将方程①改写成:这样便于考察y随x的变化是如何变化的. 当时, 从图形看,双曲线始终在直线下方,不会与之相交 而且,当越来越大时: 这样点越来越接近直线. 因此,从几何直观看,双曲线在第一象限随着x的增加,越来越接近直线但又始终不相交.根据对称性,在其他几个象限也是这样的,双曲线在四个方向上越来越接近这两条直线,但不会与这条直线相交. 换个角度来看上述情形,仍以第一象限为例, 计算点到直线(即)的距离,当时,,但d≠0 当时,,所以在第一象限内,随着的增大点会越来越接近直线,但不会与这条直线相交. 直线称之为该双曲线的渐近线. 问题4:如何才能把双曲线的图像画得比较好点? 先画出矩形和渐近线,再来画双曲线. 5、离心率 同椭圆一样,定义双曲线的半焦距与半实轴之比为离心率,即: 问题5:的范围是什么? 答: 问题6:逐渐增大时,双曲线会怎么变化? 答:开口越来越大. 先通过3个具体例子比较来看: 然后分析渐近线的斜率的绝对值: e 越趋近于1 ,则 越小,双曲线的渐近线所夹的双曲线区域越狭窄; e 越来越大时,则 越大,双曲线的渐近线所夹的双曲线区域越开阔. 2、双曲线的标准方程为: 请大家类比椭圆写出方程②,即焦点在轴上的双曲线的几何性质: (1)范围: (2)对称性: 对称轴:轴和轴 对称中心:原点 (3)顶点坐标: 实轴:线段 虚轴:线段 (4)渐近线方程: (5)离心率:
6分钟 例 题 例 求下列方程表示的双曲线的实轴长、焦点坐标、离心率及渐近线方程. 解:(1)由方程可知,焦点在轴上,且, 所以 所以实轴长,焦点坐标为: 离心率: 渐近线方程为: (2)将双曲线方程化成标准方程形式: 可知焦点在轴上,且, 所以,即 所以实轴长,焦点坐标为: 离心率: 渐近线方程为:
2分钟 课 堂 小 结 1、利用双曲线的标准方程来研究双曲线的几何性质,再次体会用代数方程研究曲线性质的思想和方法; 2、双曲线的几何性质和椭圆类似,注意它们的不同,尤其要重视对渐近线的认识,要从几何和代数两个角度加以理解; 3、在具体表示几何性质时,要区分焦点在x轴或y轴.
1分钟 课 后 作 业 课本P148,练习A第1题,练习B第1题. A1:写出的实轴长、虚轴长、焦点坐标、渐近线方程. B1:求双曲线实轴长、虚轴长、焦点坐标、离心率及渐近线方程.
