1.2 空间向量在立体几何中的应用小结 教学设计(表格式)
文档属性
| 名称 | 1.2 空间向量在立体几何中的应用小结 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 424.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 17:45:36 | ||
图片预览

文档简介
教学设计
教学基本信息
课题 空间向量在立体几何中的应用
学科 数学 学段: 第四学段 年级 高二
教材 书名: 普通高中教科书数学选择性必修第一册B版 出版社:人民教育出版社 出版日期: 2019 年 8 月
教学目标及教学重点、难点
复习用空间向量刻画空间中的直线和平面的方法,掌握对空间中线与线、线与面、面与面的平行和垂直关系的向量表示; 复习用空间向量求解空间中的角和距离的方法 着重培养学生的观察能力、抽象概括能力、逻辑推理能力和空间想象能力,建立正确的空间直角坐标系,熟练掌握直线的方向向量、平面的法向量的求解方法,并会用直线的方向向量、平面的法向量表达平行、垂直等位置关系,会求解空间中的角和距离. 共设计1道例题,体会空间向量在问题求解、求证中的使用方法,并熟悉它们的计算要求,让学生能够通过解法比较,在题目中灵活选择传统几何法或空间向量法.
教学过程(表格描述)
教学环节 主要教学活动 设置意图
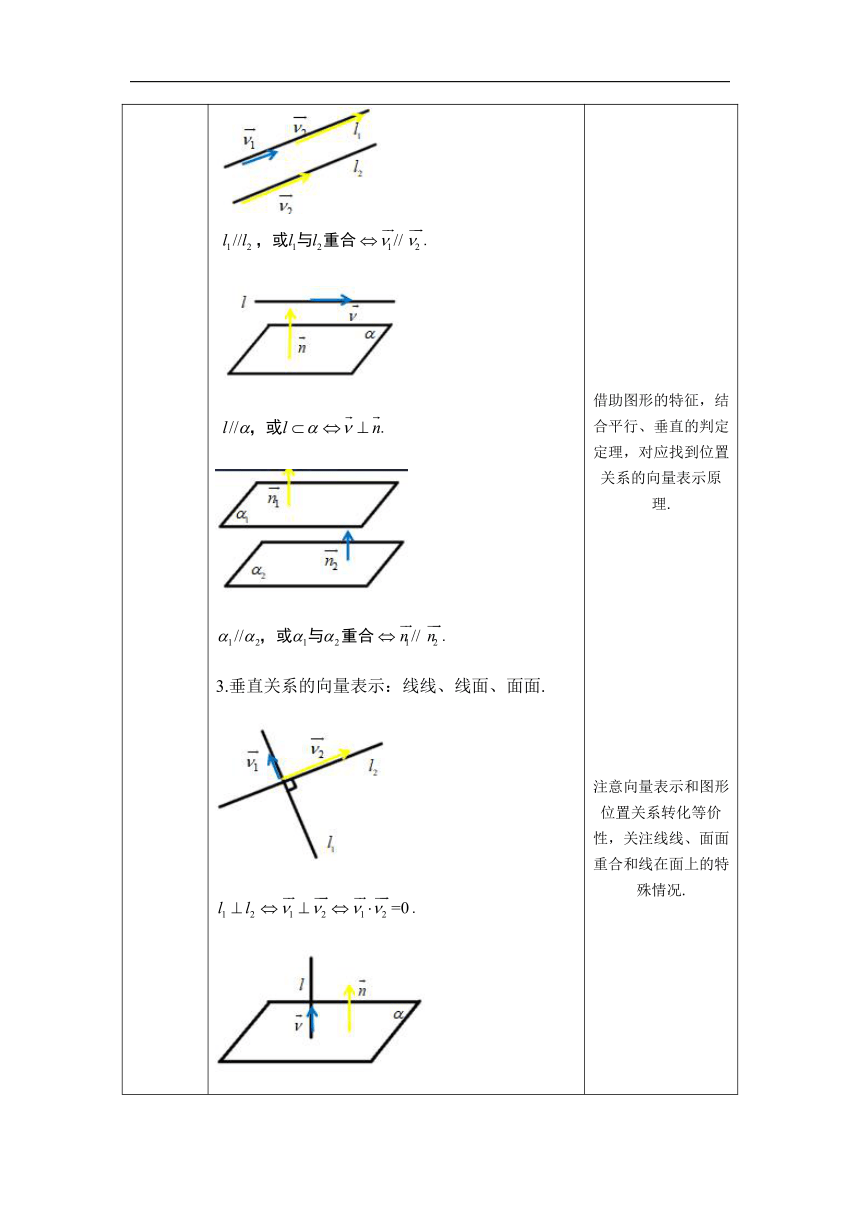
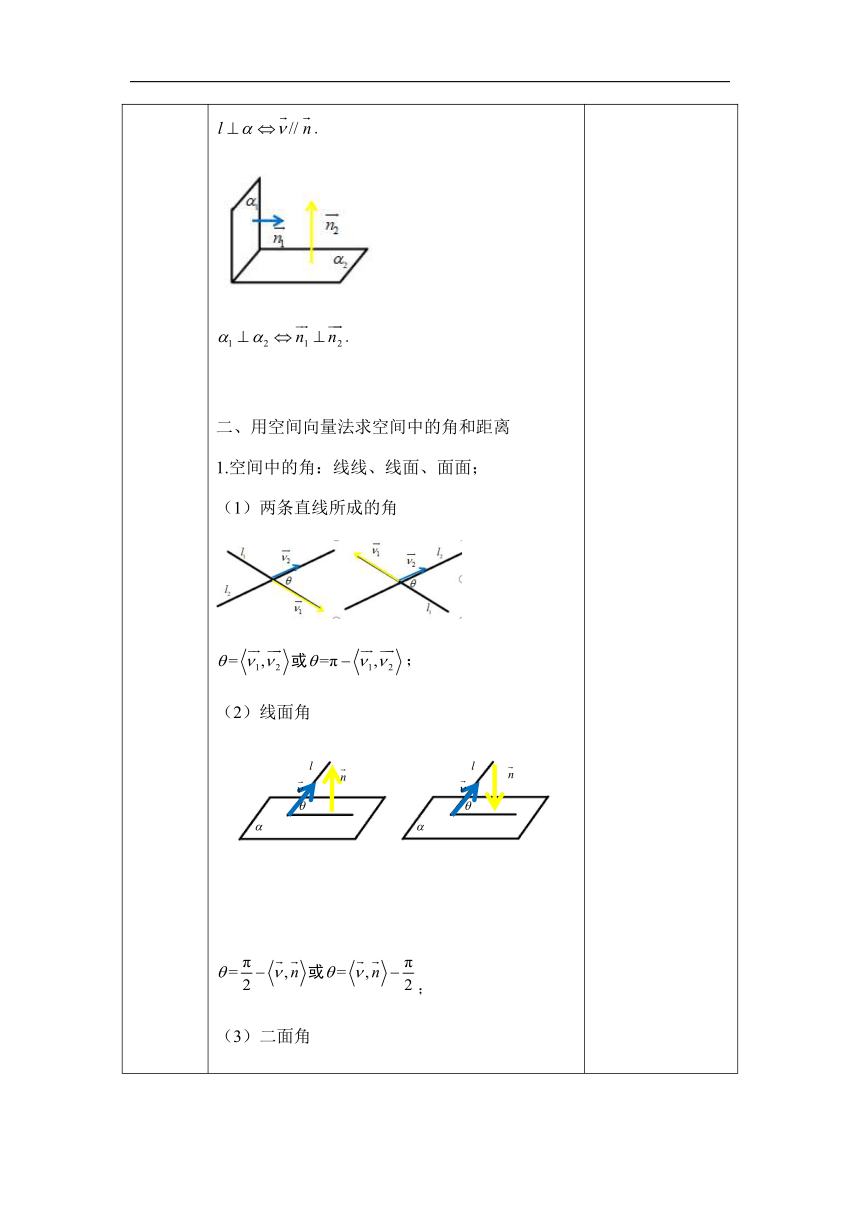
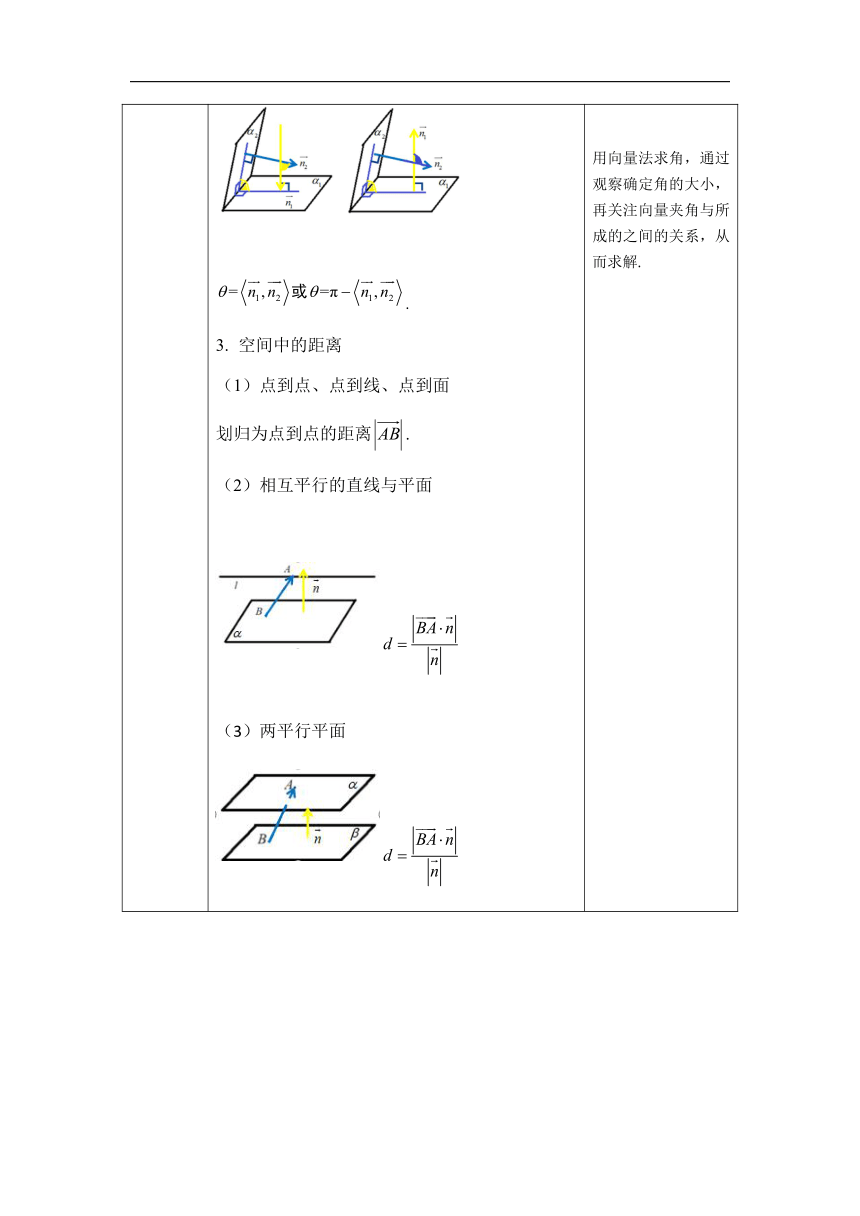
复习总结 用空间向量法刻画空间中的直线与平面 直线的方向向量与平面的法向量; 平行关系的向量表示:线线、线面、面面; 3.垂直关系的向量表示:线线、线面、面面. 二、用空间向量法求空间中的角和距离 1.空间中的角:线线、线面、面面; (1)两条直线所成的角 ; (2)线面角 (2) ; 二面角 . 空间中的距离 点到点、点到线、点到面 划归为点到点的距离. 相互平行的直线与平面 两平行平面 复习回顾梳理直线方向向量与平面的法向量在表示位置关系中的方法. 借助图形的特征,结合平行、垂直的判定定理,对应找到位置关系的向量表示原理. 注意向量表示和图形位置关系转化等价性,关注线线、面面重合和线在面上的特殊情况. 用向量法求角,通过观察确定角的大小,再关注向量夹角与所成的之间的关系,从而求解.
例题 (1) (3) 用空间向量的方法求解,关键在建系(右手系),找到线面垂直确立z轴. 用向量法求解二面角关键两个步骤:(1)求解或找到两平面的法向量;(2)计算两个法向量的夹角. 做立体几何的题目要重视观察法,通过确定二面角的大小,确定二面角的大小和两平面法向量夹角的关系. 第(3)问中判断直线与平面是否相交,是运用了位置关系的排除法,先判断线不在面内,再证明线面不平行,划归为直线方向向量与平面法向量是否垂直的判断,通过向量的内积计算来完成,比较简便.
总结 用空间向量法表示直线与平面的位置关系 用空间向量法求角 用空间向量法求距离 学习通过表格的形式梳理知识点,注意公式之间的区别和联系.
作业 教材第63页复习题B组 第10题 如图,三棱锥中,面ABC与面DBC互相垂直,且,.求: AD所在直线和平面BCD所成角的大小; AD所在直线与直线BC所成角的大小; 二面角的正弦值. 教材第64页复习题C组 第6题 如图,四棱锥的底面是正方形,每条侧棱的长都是底面边长的倍,为侧棱上的点. 求证:; 若,求二面角的大小; 在(2)的条件下,侧棱上是否存在一点,使得. 若存在,求的值;若不存在,试说明理由. 复习本节课的学习内容,体会用空间向量法求二面角的原理和作法.
教学基本信息
课题 空间向量在立体几何中的应用
学科 数学 学段: 第四学段 年级 高二
教材 书名: 普通高中教科书数学选择性必修第一册B版 出版社:人民教育出版社 出版日期: 2019 年 8 月
教学目标及教学重点、难点
复习用空间向量刻画空间中的直线和平面的方法,掌握对空间中线与线、线与面、面与面的平行和垂直关系的向量表示; 复习用空间向量求解空间中的角和距离的方法 着重培养学生的观察能力、抽象概括能力、逻辑推理能力和空间想象能力,建立正确的空间直角坐标系,熟练掌握直线的方向向量、平面的法向量的求解方法,并会用直线的方向向量、平面的法向量表达平行、垂直等位置关系,会求解空间中的角和距离. 共设计1道例题,体会空间向量在问题求解、求证中的使用方法,并熟悉它们的计算要求,让学生能够通过解法比较,在题目中灵活选择传统几何法或空间向量法.
教学过程(表格描述)
教学环节 主要教学活动 设置意图
复习总结 用空间向量法刻画空间中的直线与平面 直线的方向向量与平面的法向量; 平行关系的向量表示:线线、线面、面面; 3.垂直关系的向量表示:线线、线面、面面. 二、用空间向量法求空间中的角和距离 1.空间中的角:线线、线面、面面; (1)两条直线所成的角 ; (2)线面角 (2) ; 二面角 . 空间中的距离 点到点、点到线、点到面 划归为点到点的距离. 相互平行的直线与平面 两平行平面 复习回顾梳理直线方向向量与平面的法向量在表示位置关系中的方法. 借助图形的特征,结合平行、垂直的判定定理,对应找到位置关系的向量表示原理. 注意向量表示和图形位置关系转化等价性,关注线线、面面重合和线在面上的特殊情况. 用向量法求角,通过观察确定角的大小,再关注向量夹角与所成的之间的关系,从而求解.
例题 (1) (3) 用空间向量的方法求解,关键在建系(右手系),找到线面垂直确立z轴. 用向量法求解二面角关键两个步骤:(1)求解或找到两平面的法向量;(2)计算两个法向量的夹角. 做立体几何的题目要重视观察法,通过确定二面角的大小,确定二面角的大小和两平面法向量夹角的关系. 第(3)问中判断直线与平面是否相交,是运用了位置关系的排除法,先判断线不在面内,再证明线面不平行,划归为直线方向向量与平面法向量是否垂直的判断,通过向量的内积计算来完成,比较简便.
总结 用空间向量法表示直线与平面的位置关系 用空间向量法求角 用空间向量法求距离 学习通过表格的形式梳理知识点,注意公式之间的区别和联系.
作业 教材第63页复习题B组 第10题 如图,三棱锥中,面ABC与面DBC互相垂直,且,.求: AD所在直线和平面BCD所成角的大小; AD所在直线与直线BC所成角的大小; 二面角的正弦值. 教材第64页复习题C组 第6题 如图,四棱锥的底面是正方形,每条侧棱的长都是底面边长的倍,为侧棱上的点. 求证:; 若,求二面角的大小; 在(2)的条件下,侧棱上是否存在一点,使得. 若存在,求的值;若不存在,试说明理由. 复习本节课的学习内容,体会用空间向量法求二面角的原理和作法.
