1.2.1 空间中的点、直线与空间向量 教学设计(表格式)
文档属性
| 名称 | 1.2.1 空间中的点、直线与空间向量 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 581.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 00:00:00 | ||
图片预览



文档简介
《空间中的点、直线与空间向量》教学设计
本节主要学空间中的点、直线与空间向量.在向量坐标化的基础上,将空间中点、直线的位置关系,转化为向量语言,进而运用向量的坐标表示,从而实现运用空间向量解决立体几何问题,为学生学习立体几何提供了新的方法和新的观点,为培养学生思维提供了更广阔的空间.
课程目标 学科素养
A.理解位置向量、方向向量的概念 B.能利用直线的方向向量解决两条直线所成的角问题. C.初步了解两条异面直线的距离的定义. 1.数学抽象:点的位置向量、直线的方向向量 2.逻辑推理:用直线的方向向量解决两条直线所成的角 3.直观想象:点的位置向量、直线的方向向量 4.数学运算:求解异面直线所成的角,直线的平行与垂直判断
1.教学重点:点的位置向量与直线的方向向量的概念及其应用
2.教学难点:用直线的方向向量解决两条直线所成的角,判断两直线平行与垂直
多媒体
教学过程 教学设计意图 核心素养目标
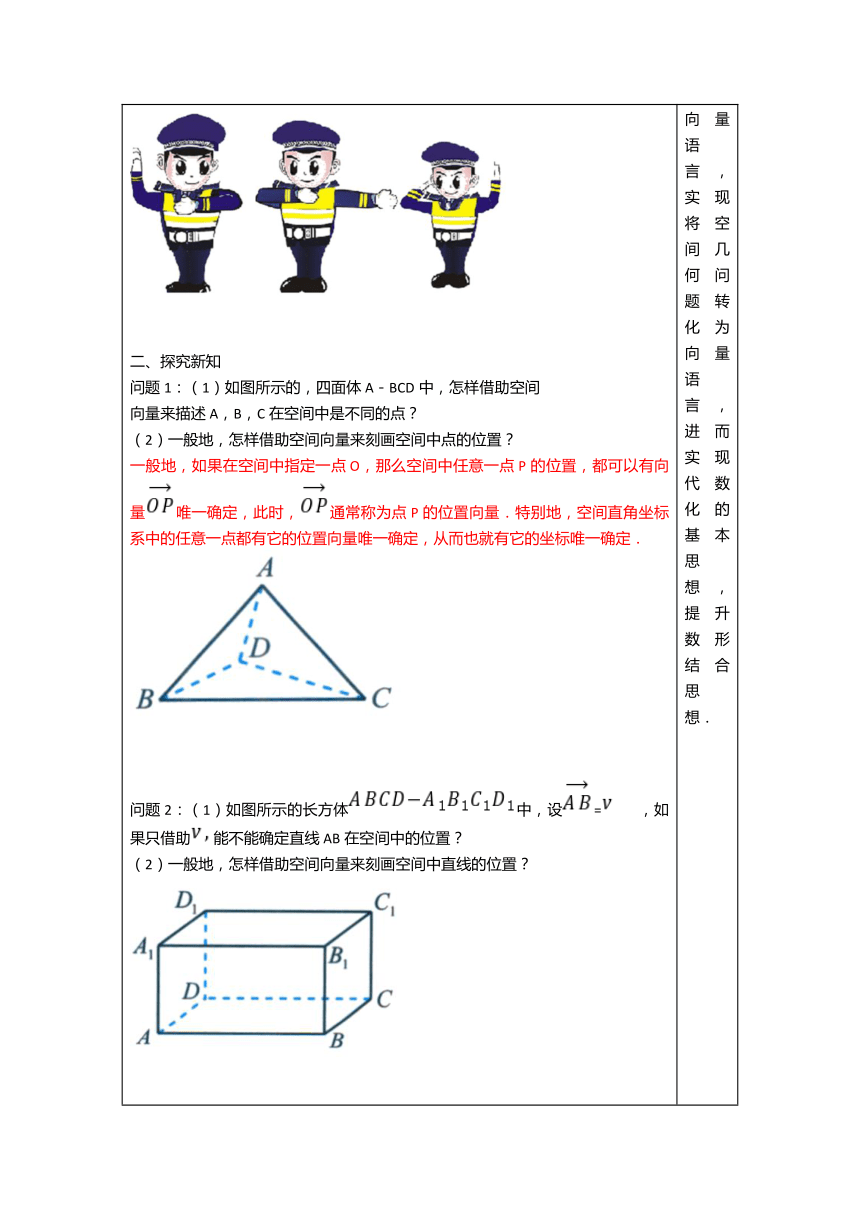
一、情境导学 在交通繁忙的路口,交警常常借助专用的手势,作为 “语言” 来指挥交通.在不同领域有不同的“语言”,研究空间中的直线及其夹角也可以先提炼出与之有关联的“向量语言”来进行.同学们,你们知道是如何提炼的吗?提炼出来后又将如何运用呢?
二、探究新知 问题1:(1)如图所示的,四面体A-BCD中,怎样借助空间 向量来描述A,B,C在空间中是不同的点? (2)一般地,怎样借助空间向量来刻画空间中点的位置? 一般地,如果在空间中指定一点O,那么空间中任意一点P的位置,都可以有向量唯一确定,此时,通常称为点P的位置向量.特别地,空间直角坐标系中的任意一点都有它的位置向量唯一确定,从而也就有它的坐标唯一确定.
问题2:(1)如图所示的长方体中,设=,如果只借助能不能确定直线AB在空间中的位置? (2)一般地,怎样借助空间向量来刻画空间中直线的位置?
一般地如果是空间中的一条直线,空间中的一个非零向量,且表示的有向线段所在的直线与平行或重合,则称为直线L的一个方向向量,此时也称与直线平行,记作
1.点的位置向量、直线的方向向量
位置向量 一般地,如果在空间中指定一点O,那么空间中任意一点P的位置,都可以由向量唯一确定,此时,通常称为点P的位置向量 方向向量 一般地,如果l是空间中的一条直线,v是空间中的一个非零向量,且表示v的有向线段所在的直线与l平行或重合,则称v为直线l的一个方向向量.此时,也称向量v与直线l平行,记作v∥l
思考:空间一条直线的方向向量唯一吗? 提示:不唯一. 2.空间中两条直线所成的角 设v,v分别是空间中直线l,l的方向向量,且l与l所成角的大小为θ. 则θ=或θ=π-. 特别地,sinθ=sin,cosθ=|cos|;l⊥l = v·v=0.
1.已知直线a,b的方向向量分别是m=(1,k,1),n=(k,k+2,2),若a⊥b. 则k= . 解析:∵a⊥b,∴m⊥n,即m·n=0.∴k+k+2k+2=0. 即k+3k+2=0,∴k=-2或k=-1. 答案:-1或-2 3.两条异面直线的距离 一般地,如果l与l是空间中两条异面直线,A∈l,B∈l,AB⊥l,AB⊥l,则称AB为l与l的公垂线段.并且空间中任意两条异面直线的公垂线段都存在并且唯一.两条异面直线的公垂线段的长,称为这两条异面直线之间的距离. 思考:怎样在空间直角坐标系中求两条异面直线的公垂线段的长度? 提示:利用向量共线、向量垂直的条件建立方程组,求出公垂线段对应的向量,准确找出公垂线段在图中的位置,运用向量求出公垂线段的长度.
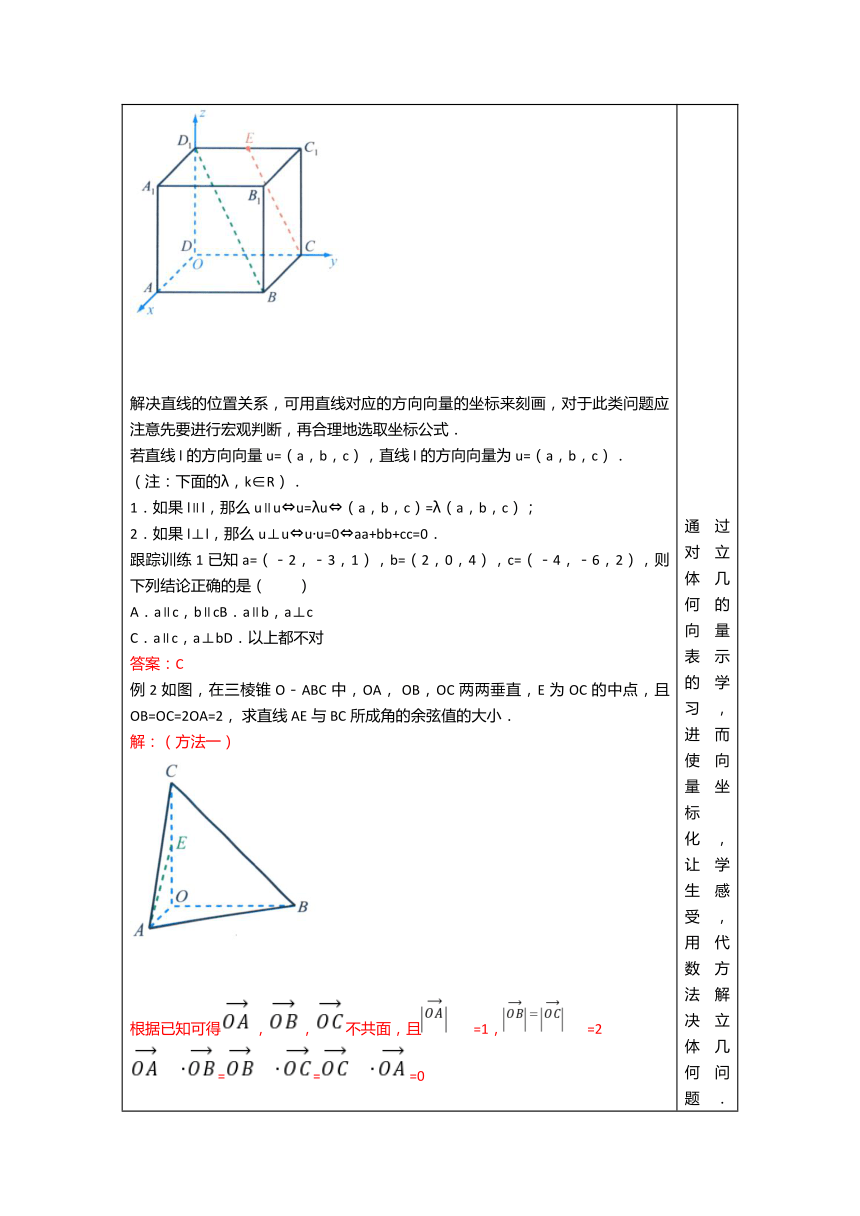
例1.已知正方体中,E为的中点. 求证:直线与直线不平行 证明:以为原点,,,的方向分别为轴正方向,正方体的棱长为单位长度,建立如图所示的空间直角坐标系,则(0,0,1), 所以== 又因为所以与不平行. 因为为直线的一个方向,向量为直线的一个方向,向量,当时必有由上可知直线与直线不平行
解决直线的位置关系,可用直线对应的方向向量的坐标来刻画,对于此类问题应注意先要进行宏观判断,再合理地选取坐标公式. 若直线l的方向向量u=(a,b,c),直线l的方向向量为u=(a,b,c). (注:下面的λ,k∈R). 1.如果l∥l,那么u∥u u=λu (a,b,c)=λ(a,b,c); 2.如果l⊥l,那么u⊥u u·u=0 aa+bb+cc=0. 跟踪训练1已知a=(-2,-3,1),b=(2,0,4),c=(-4,-6,2),则下列结论正确的是( ) A.a∥c,b∥cB.a∥b,a⊥c C.a∥c,a⊥bD.以上都不对 答案:C 例2如图,在三棱锥O-ABC中,OA, OB,OC两两垂直,E为OC的中点,且OB=OC=2OA=2, 求直线AE与BC所成角的余弦值的大小. 解:(方法一)
根据已知可得,,不共面,且=1,=2 ===0 又因为==,= 所以=()()=2,=()()=8,所以== 因此直线AE与BC所成角的余弦值的大小为. 解:(方法二)因为OA,OB,OC两两互相垂直. 所以能以O为原点,,,的方向分别 为轴正方向,建立如图所示直角坐标 系,由OB=OC=2OA=2.
可知A(0,0,1),. 所以=(-1,0,1),=(0,0,1) , 因此 所以=== 因此直线AE与BC所成角的余弦值的大小为. 解:(方法三)设OB的中点为F,连接EF,AF.由E,F分别为OC,OB中点可知EF为OBC的中位线,从而EFBC.
因此直线AE与BC所成角的大小等于直线AE与EF所成角的大小.又易知OA=OE=OF=1,而且OA,OE,OF两两垂直. 因此AE=EF=AF= 所以是等边三角形,从而. 因此直线AE与BC所成角的大小为 求解异面直线夹角方法,常用的就是建系后利用向量的坐标处理,除此之外还要注意其他方法的要领. (1)传统法:作出与异面直线所成角相等的平面角,进而构造三角形求解.这种方法灵活技巧性强,强调对夹角定义的挖掘.
(2)向量法:在两异面直线a与b上分别取点A,B和C,D,则可分别为a,b的方向向量,则cosθ=.这一方法思路简单,不需构造,但计算量一般较大. 运用向量法常用两种途径: ①基底法 在一些不适合建立坐标系的题型中,我们经常采用取定基底的方法,这是小技巧.在由公式cos=求向量a,b的夹角时,关键是求出a·b及|a|与|b|,一般是把a,b用基向量表示出来,再求有关的量. ②坐标法 根据题目条件建立恰当的空间直角坐标系,写出相关各点的坐标,利用坐标法求线线角,避免了传统找角或作角的步骤,使过程变得简单. 跟踪训练2如图,在三棱柱OAB-OAB中,平面OBBO⊥平面OAB,∠OOB=60°,∠AOB=90°,且OB=OO=2,OA=,求异面直线AB与AO所成角的余弦值的大小.
解:以O为坐标原点,的方向为x轴,y轴的正方向.建立如图所示的空间直角坐标系. 则O(0,0,0),O(0,1,),A(,0,0),A(,1,),B(0,2,0). ∴=(-,1,-),=(,-1,-). ∴|cos<>|==. ∴异面直线AB与AO所成角的余弦值为.
例3如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°. E,F分别为AC,DC的中点. 求证:EF⊥BC.
证明:由题意,以点B为坐标原点,在平面DBC内过点B作垂直于BC的直线为x轴,BC所在直线为y轴. 在平面ABC内过点B作垂直BC的直线为z轴,建立如图所示的空间直角坐标系. 易得B(0,0,0),A0,-1,,D(,-1,0),C(0,2,0). 因而E0,,F,0,,所以=,0,-,=(0,2,0). 则=0,所以,即EF⊥BC.
证明两直线垂直的基本步骤 建立空间直角坐标系→写出点的坐标→求直线的方向向量→证明向量垂直→得到两直线垂直.对于几何体为三棱锥的情况一定要注意建系的重要性,要使已知数据和所用的点更多地落在坐标平面或坐标轴上为标准.本例中要充分抓住平面ABC和平面BCD互相垂直这一条件. 跟踪训练3已知正三棱柱ABC-ABC的各棱长都为1,M是底面上BC边的中点,N是侧棱CC上的点,且CN=CC.求证:AB⊥MN.
证明:设AB中点为O,作OO∥AA.以O为坐标原点,OB所在直线为x轴,OC所在直线为y轴,OO所在直线为z轴建立如图所示的空间直角坐标系Oxyz.
由已知得A-,0,0,B,0,0,C0,,0,N0,,B,0,1. ∵M为BC中点,∴M,0. ∴=-,=(1,0,1),∴=-+0+=0. ∴,即AB⊥MN.
金题典例:如图,已知 ABCD中,AB=AC=1,∠ACD=90°,将它沿对角线AC折起,使AB与CD成60°角,求B,D间的距离.
错解:如图,因为∠ACD=90°. 所以=0,同理=0. 因为AB与CD的夹角为60°. 所以的夹角为60°. 因为. 所以||=||+||+||+2+2+2=3+2cos<>=4. 所以||=2,即B,D间的距离为2.
错因分析: 由异面直线AB与CD成60°角得到所成的角为60°,这是错误的.混淆了异面直线所成的角与向量的夹角的定义,从而致误. 向量的夹角与向量的方向有关系,且向量的夹角的范围为0≤θ≤π;异面直线的夹角与直线的方向没有关系,异面直线的夹角的范围是0<θ≤.两者的范围不一样. 正解:因为∠ACD=90°,所以=0,同理=0. 因为AB与CD的夹角为60°. 所以的夹角为60°或120°. 因为. 所以||=||+||+||+2+2+2=3+2cos<>. 当所成的角为60°时,||=3+2cos<>=4,所以||=2,即B、D间的距离为2;当所成的角为120°时,||=3+2cos<>=2,所以||=. 综上可得,B,D间的距离为2或.
创设问题情境,引导学生体会运用向量语言,实现将空间几何问题转化为向量语言,进而实现代数化的基本思想,提升数形结合思想.
由问题引导,让学生感受到运用向量语言表示立体几何要素,实现立体几何向量化.
通过对立体几何的向量表示的学习,进而使向量坐标化,让学生感受,用代数方法解决立体几何问题.发展学生逻辑推理,数学抽象和数学运算的核心素养.
通过典型例题的分析和解决,让学生感受空间向量坐标运算在解决空间几何中的应用.发展学生数学抽象、逻辑推理的核心素养.
通过典例解析,进一步让学生体会空间向量坐标在解决立体几何中的应用,提升推理论证能力,提高学生的数学运算及逻辑推理的核心素养.
三、达标检测 1.若A(1,0,-1),B(2,1,2)在直线l上,则直线l的一个方向向量是( ) A.(2,2,6) B.(-1,1,3) C.(3,1,1) D.(-3,0,1) 解析:∵A,B在直线l上,∴=(1,1,3),与共线的向量(2,2,6)可以是直线l的一个方向向量. 答案:A 2.设直线l,l的方向向量分别为a=(-2,2,1),b=(3,-2,m),若l⊥l,则m等于( ) A.-2 B.2 C.10 D.6 解析:因为a⊥b,故a·b=0,即-2×3+2×(-2)+m=0,解得m=10. 答案:C 3.已知a,b是异面直线,A,B∈a,C,D∈b,AC⊥b,BD⊥b,且AB=2,CD=1,则a,b所成的角是 . 解析:∵=()·=||=1. ∴cos<>=.所以<>=. 答案: 4.已知正方体ABCD-ABCD中,E是棱CC上的动点. 求证:AE⊥BD. 证明:以D为坐标原点,以DA,DC,DD所在直线分别为x轴、y轴、z轴建立空间直角坐标系.设正方体棱长为a,则A(a,0,0),B(a,a,0),C(0,a,0),A(a,0,a),C(0,a,a).
设E(0,a,b)(0≤b≤a),=(-a,a,b-a). =(-a,-a,0),=a-a+(b-a)·0=0. ∴,即AE⊥BD.
通过练习巩固本节所学知识,通过学生解决问题,发展学生的数学运算、逻辑推理、数学建模的核心素养.
四、小结
五、课时练
通过总结,让学生进一步巩固本节所学内容,提高概括能力.
教学中主要突出创设问题情景和问题引导,通过生活中的手势语言类比运用向量语言表示立体几何要素,进而在将向量坐标化,让学生初步体会空间向量坐标化的基本思想,并以此来激发学生的探究心理.教学设计尽量做到注意学生的心理特点和认知规律,触发学生的思维,使教学过程真正成为学生的学习过程,以思维教学代替单纯的记忆教学.注意在探究问题时留给学生充分的时间,使数学教学成为数学活动的教学.从而发展学生的直观想象、逻辑推理、数学建模的核心素养.
本节主要学空间中的点、直线与空间向量.在向量坐标化的基础上,将空间中点、直线的位置关系,转化为向量语言,进而运用向量的坐标表示,从而实现运用空间向量解决立体几何问题,为学生学习立体几何提供了新的方法和新的观点,为培养学生思维提供了更广阔的空间.
课程目标 学科素养
A.理解位置向量、方向向量的概念 B.能利用直线的方向向量解决两条直线所成的角问题. C.初步了解两条异面直线的距离的定义. 1.数学抽象:点的位置向量、直线的方向向量 2.逻辑推理:用直线的方向向量解决两条直线所成的角 3.直观想象:点的位置向量、直线的方向向量 4.数学运算:求解异面直线所成的角,直线的平行与垂直判断
1.教学重点:点的位置向量与直线的方向向量的概念及其应用
2.教学难点:用直线的方向向量解决两条直线所成的角,判断两直线平行与垂直
多媒体
教学过程 教学设计意图 核心素养目标
一、情境导学 在交通繁忙的路口,交警常常借助专用的手势,作为 “语言” 来指挥交通.在不同领域有不同的“语言”,研究空间中的直线及其夹角也可以先提炼出与之有关联的“向量语言”来进行.同学们,你们知道是如何提炼的吗?提炼出来后又将如何运用呢?
二、探究新知 问题1:(1)如图所示的,四面体A-BCD中,怎样借助空间 向量来描述A,B,C在空间中是不同的点? (2)一般地,怎样借助空间向量来刻画空间中点的位置? 一般地,如果在空间中指定一点O,那么空间中任意一点P的位置,都可以有向量唯一确定,此时,通常称为点P的位置向量.特别地,空间直角坐标系中的任意一点都有它的位置向量唯一确定,从而也就有它的坐标唯一确定.
问题2:(1)如图所示的长方体中,设=,如果只借助能不能确定直线AB在空间中的位置? (2)一般地,怎样借助空间向量来刻画空间中直线的位置?
一般地如果是空间中的一条直线,空间中的一个非零向量,且表示的有向线段所在的直线与平行或重合,则称为直线L的一个方向向量,此时也称与直线平行,记作
1.点的位置向量、直线的方向向量
位置向量 一般地,如果在空间中指定一点O,那么空间中任意一点P的位置,都可以由向量唯一确定,此时,通常称为点P的位置向量 方向向量 一般地,如果l是空间中的一条直线,v是空间中的一个非零向量,且表示v的有向线段所在的直线与l平行或重合,则称v为直线l的一个方向向量.此时,也称向量v与直线l平行,记作v∥l
思考:空间一条直线的方向向量唯一吗? 提示:不唯一. 2.空间中两条直线所成的角 设v,v分别是空间中直线l,l的方向向量,且l与l所成角的大小为θ. 则θ=
1.已知直线a,b的方向向量分别是m=(1,k,1),n=(k,k+2,2),若a⊥b. 则k= . 解析:∵a⊥b,∴m⊥n,即m·n=0.∴k+k+2k+2=0. 即k+3k+2=0,∴k=-2或k=-1. 答案:-1或-2 3.两条异面直线的距离 一般地,如果l与l是空间中两条异面直线,A∈l,B∈l,AB⊥l,AB⊥l,则称AB为l与l的公垂线段.并且空间中任意两条异面直线的公垂线段都存在并且唯一.两条异面直线的公垂线段的长,称为这两条异面直线之间的距离. 思考:怎样在空间直角坐标系中求两条异面直线的公垂线段的长度? 提示:利用向量共线、向量垂直的条件建立方程组,求出公垂线段对应的向量,准确找出公垂线段在图中的位置,运用向量求出公垂线段的长度.
例1.已知正方体中,E为的中点. 求证:直线与直线不平行 证明:以为原点,,,的方向分别为轴正方向,正方体的棱长为单位长度,建立如图所示的空间直角坐标系,则(0,0,1), 所以== 又因为所以与不平行. 因为为直线的一个方向,向量为直线的一个方向,向量,当时必有由上可知直线与直线不平行
解决直线的位置关系,可用直线对应的方向向量的坐标来刻画,对于此类问题应注意先要进行宏观判断,再合理地选取坐标公式. 若直线l的方向向量u=(a,b,c),直线l的方向向量为u=(a,b,c). (注:下面的λ,k∈R). 1.如果l∥l,那么u∥u u=λu (a,b,c)=λ(a,b,c); 2.如果l⊥l,那么u⊥u u·u=0 aa+bb+cc=0. 跟踪训练1已知a=(-2,-3,1),b=(2,0,4),c=(-4,-6,2),则下列结论正确的是( ) A.a∥c,b∥cB.a∥b,a⊥c C.a∥c,a⊥bD.以上都不对 答案:C 例2如图,在三棱锥O-ABC中,OA, OB,OC两两垂直,E为OC的中点,且OB=OC=2OA=2, 求直线AE与BC所成角的余弦值的大小. 解:(方法一)
根据已知可得,,不共面,且=1,=2 ===0 又因为==,= 所以=()()=2,=()()=8,所以== 因此直线AE与BC所成角的余弦值的大小为. 解:(方法二)因为OA,OB,OC两两互相垂直. 所以能以O为原点,,,的方向分别 为轴正方向,建立如图所示直角坐标 系,由OB=OC=2OA=2.
可知A(0,0,1),. 所以=(-1,0,1),=(0,0,1) , 因此 所以=== 因此直线AE与BC所成角的余弦值的大小为. 解:(方法三)设OB的中点为F,连接EF,AF.由E,F分别为OC,OB中点可知EF为OBC的中位线,从而EFBC.
因此直线AE与BC所成角的大小等于直线AE与EF所成角的大小.又易知OA=OE=OF=1,而且OA,OE,OF两两垂直. 因此AE=EF=AF= 所以是等边三角形,从而. 因此直线AE与BC所成角的大小为 求解异面直线夹角方法,常用的就是建系后利用向量的坐标处理,除此之外还要注意其他方法的要领. (1)传统法:作出与异面直线所成角相等的平面角,进而构造三角形求解.这种方法灵活技巧性强,强调对夹角定义的挖掘.
(2)向量法:在两异面直线a与b上分别取点A,B和C,D,则可分别为a,b的方向向量,则cosθ=.这一方法思路简单,不需构造,但计算量一般较大. 运用向量法常用两种途径: ①基底法 在一些不适合建立坐标系的题型中,我们经常采用取定基底的方法,这是小技巧.在由公式cos
解:以O为坐标原点,的方向为x轴,y轴的正方向.建立如图所示的空间直角坐标系. 则O(0,0,0),O(0,1,),A(,0,0),A(,1,),B(0,2,0). ∴=(-,1,-),=(,-1,-). ∴|cos<>|==. ∴异面直线AB与AO所成角的余弦值为.
例3如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°. E,F分别为AC,DC的中点. 求证:EF⊥BC.
证明:由题意,以点B为坐标原点,在平面DBC内过点B作垂直于BC的直线为x轴,BC所在直线为y轴. 在平面ABC内过点B作垂直BC的直线为z轴,建立如图所示的空间直角坐标系. 易得B(0,0,0),A0,-1,,D(,-1,0),C(0,2,0). 因而E0,,F,0,,所以=,0,-,=(0,2,0). 则=0,所以,即EF⊥BC.
证明两直线垂直的基本步骤 建立空间直角坐标系→写出点的坐标→求直线的方向向量→证明向量垂直→得到两直线垂直.对于几何体为三棱锥的情况一定要注意建系的重要性,要使已知数据和所用的点更多地落在坐标平面或坐标轴上为标准.本例中要充分抓住平面ABC和平面BCD互相垂直这一条件. 跟踪训练3已知正三棱柱ABC-ABC的各棱长都为1,M是底面上BC边的中点,N是侧棱CC上的点,且CN=CC.求证:AB⊥MN.
证明:设AB中点为O,作OO∥AA.以O为坐标原点,OB所在直线为x轴,OC所在直线为y轴,OO所在直线为z轴建立如图所示的空间直角坐标系Oxyz.
由已知得A-,0,0,B,0,0,C0,,0,N0,,B,0,1. ∵M为BC中点,∴M,0. ∴=-,=(1,0,1),∴=-+0+=0. ∴,即AB⊥MN.
金题典例:如图,已知 ABCD中,AB=AC=1,∠ACD=90°,将它沿对角线AC折起,使AB与CD成60°角,求B,D间的距离.
错解:如图,因为∠ACD=90°. 所以=0,同理=0. 因为AB与CD的夹角为60°. 所以的夹角为60°. 因为. 所以||=||+||+||+2+2+2=3+2cos<>=4. 所以||=2,即B,D间的距离为2.
错因分析: 由异面直线AB与CD成60°角得到所成的角为60°,这是错误的.混淆了异面直线所成的角与向量的夹角的定义,从而致误. 向量的夹角与向量的方向有关系,且向量的夹角的范围为0≤θ≤π;异面直线的夹角与直线的方向没有关系,异面直线的夹角的范围是0<θ≤.两者的范围不一样. 正解:因为∠ACD=90°,所以=0,同理=0. 因为AB与CD的夹角为60°. 所以的夹角为60°或120°. 因为. 所以||=||+||+||+2+2+2=3+2cos<>. 当所成的角为60°时,||=3+2cos<>=4,所以||=2,即B、D间的距离为2;当所成的角为120°时,||=3+2cos<>=2,所以||=. 综上可得,B,D间的距离为2或.
创设问题情境,引导学生体会运用向量语言,实现将空间几何问题转化为向量语言,进而实现代数化的基本思想,提升数形结合思想.
由问题引导,让学生感受到运用向量语言表示立体几何要素,实现立体几何向量化.
通过对立体几何的向量表示的学习,进而使向量坐标化,让学生感受,用代数方法解决立体几何问题.发展学生逻辑推理,数学抽象和数学运算的核心素养.
通过典型例题的分析和解决,让学生感受空间向量坐标运算在解决空间几何中的应用.发展学生数学抽象、逻辑推理的核心素养.
通过典例解析,进一步让学生体会空间向量坐标在解决立体几何中的应用,提升推理论证能力,提高学生的数学运算及逻辑推理的核心素养.
三、达标检测 1.若A(1,0,-1),B(2,1,2)在直线l上,则直线l的一个方向向量是( ) A.(2,2,6) B.(-1,1,3) C.(3,1,1) D.(-3,0,1) 解析:∵A,B在直线l上,∴=(1,1,3),与共线的向量(2,2,6)可以是直线l的一个方向向量. 答案:A 2.设直线l,l的方向向量分别为a=(-2,2,1),b=(3,-2,m),若l⊥l,则m等于( ) A.-2 B.2 C.10 D.6 解析:因为a⊥b,故a·b=0,即-2×3+2×(-2)+m=0,解得m=10. 答案:C 3.已知a,b是异面直线,A,B∈a,C,D∈b,AC⊥b,BD⊥b,且AB=2,CD=1,则a,b所成的角是 . 解析:∵=()·=||=1. ∴cos<>=.所以<>=. 答案: 4.已知正方体ABCD-ABCD中,E是棱CC上的动点. 求证:AE⊥BD. 证明:以D为坐标原点,以DA,DC,DD所在直线分别为x轴、y轴、z轴建立空间直角坐标系.设正方体棱长为a,则A(a,0,0),B(a,a,0),C(0,a,0),A(a,0,a),C(0,a,a).
设E(0,a,b)(0≤b≤a),=(-a,a,b-a). =(-a,-a,0),=a-a+(b-a)·0=0. ∴,即AE⊥BD.
通过练习巩固本节所学知识,通过学生解决问题,发展学生的数学运算、逻辑推理、数学建模的核心素养.
四、小结
五、课时练
通过总结,让学生进一步巩固本节所学内容,提高概括能力.
教学中主要突出创设问题情景和问题引导,通过生活中的手势语言类比运用向量语言表示立体几何要素,进而在将向量坐标化,让学生初步体会空间向量坐标化的基本思想,并以此来激发学生的探究心理.教学设计尽量做到注意学生的心理特点和认知规律,触发学生的思维,使教学过程真正成为学生的学习过程,以思维教学代替单纯的记忆教学.注意在探究问题时留给学生充分的时间,使数学教学成为数学活动的教学.从而发展学生的直观想象、逻辑推理、数学建模的核心素养.
