2022--2023学年青岛版八年级数学上册第一章全等三角形 单元测试卷(含解析)
文档属性
| 名称 | 2022--2023学年青岛版八年级数学上册第一章全等三角形 单元测试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 151.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 00:00:00 | ||
图片预览



文档简介
八年级上册第一章全等三角形(单元测试卷)青岛版
一.选择题(共8小题)
1.以下列各组线段长为边能组成三角形的是( )
A.1cm,2cm,4cm B.2cm,4cm,6cm
C.4cm,6cm,8cm D.5cm,6cm,12cm
2.如图,在2×2的方格纸中,∠1+∠2等于( )
A.60° B.90° C.120° D.150°
3.小红家有一个小口瓶(如图所示),她很想知道它的内径是多少?但是尺子不能伸到里边直接测,于是她拿来了两根长度相同的细木条,并且把两根细木条的中点固定在一起,木条可以绕中点转动,这样只要量出AB的长,就可以知道玻璃瓶的内径是多少,那么△OAB≌△OCD理由是( )
A.边角边 B.角边角 C.边边边 D.角角边
4.如图,已知直角△ABC中,∠BAC=90°,∠B=56°,AD⊥BC,DE∥CA.∠ADE的度数为( )
A.56° B.34° C.44° D.46°
5.如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法中错误的是( )
A.BF=CF B.∠C+∠CAD=90°
C.∠BAF=∠CAF D.S△ABC=2S△ABF
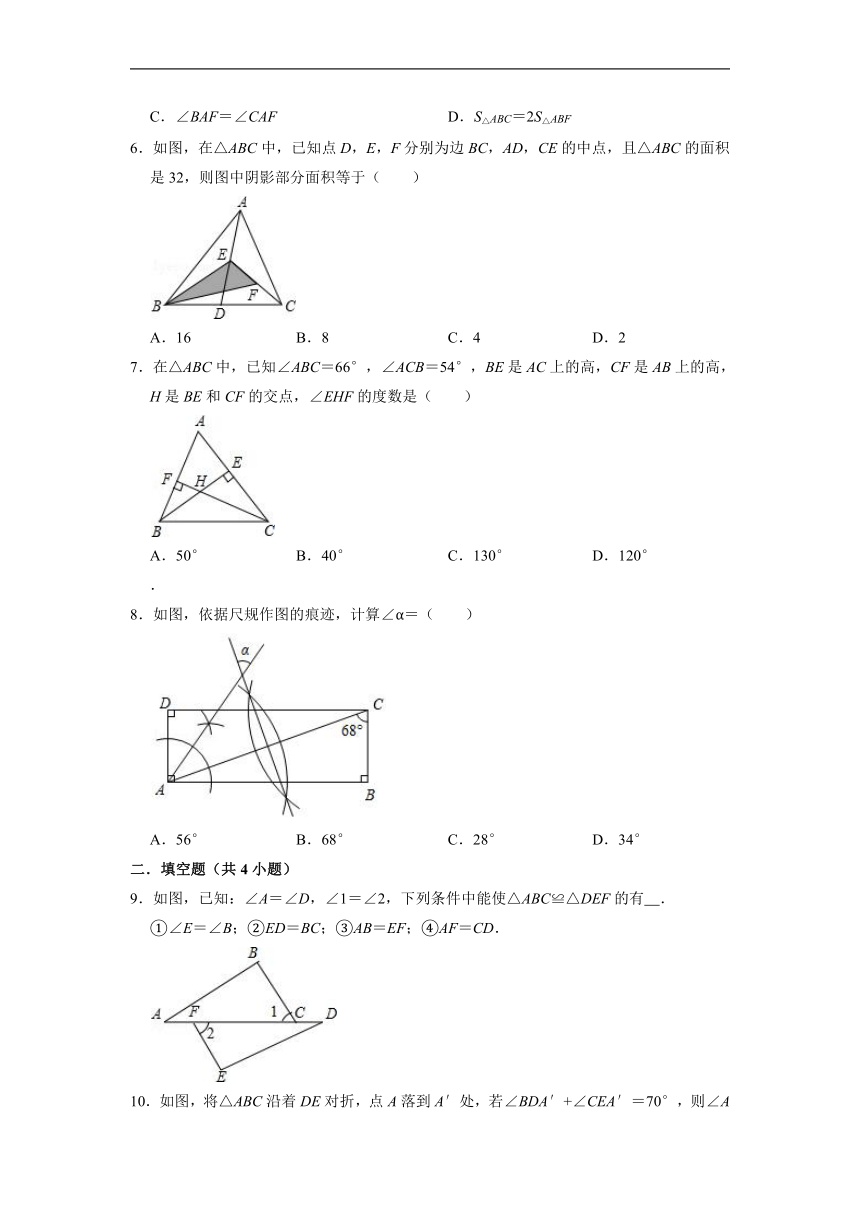
6.如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且△ABC的面积是32,则图中阴影部分面积等于( )
A.16 B.8 C.4 D.2
7.在△ABC中,已知∠ABC=66°,∠ACB=54°,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,∠EHF的度数是( )
A.50° B.40° C.130° D.120°
.
8.如图,依据尺规作图的痕迹,计算∠α=( )
A.56° B.68° C.28° D.34°
二.填空题(共4小题)
9.如图,已知:∠A=∠D,∠1=∠2,下列条件中能使△ABC≌△DEF的有 .
①∠E=∠B;②ED=BC;③AB=EF;④AF=CD.
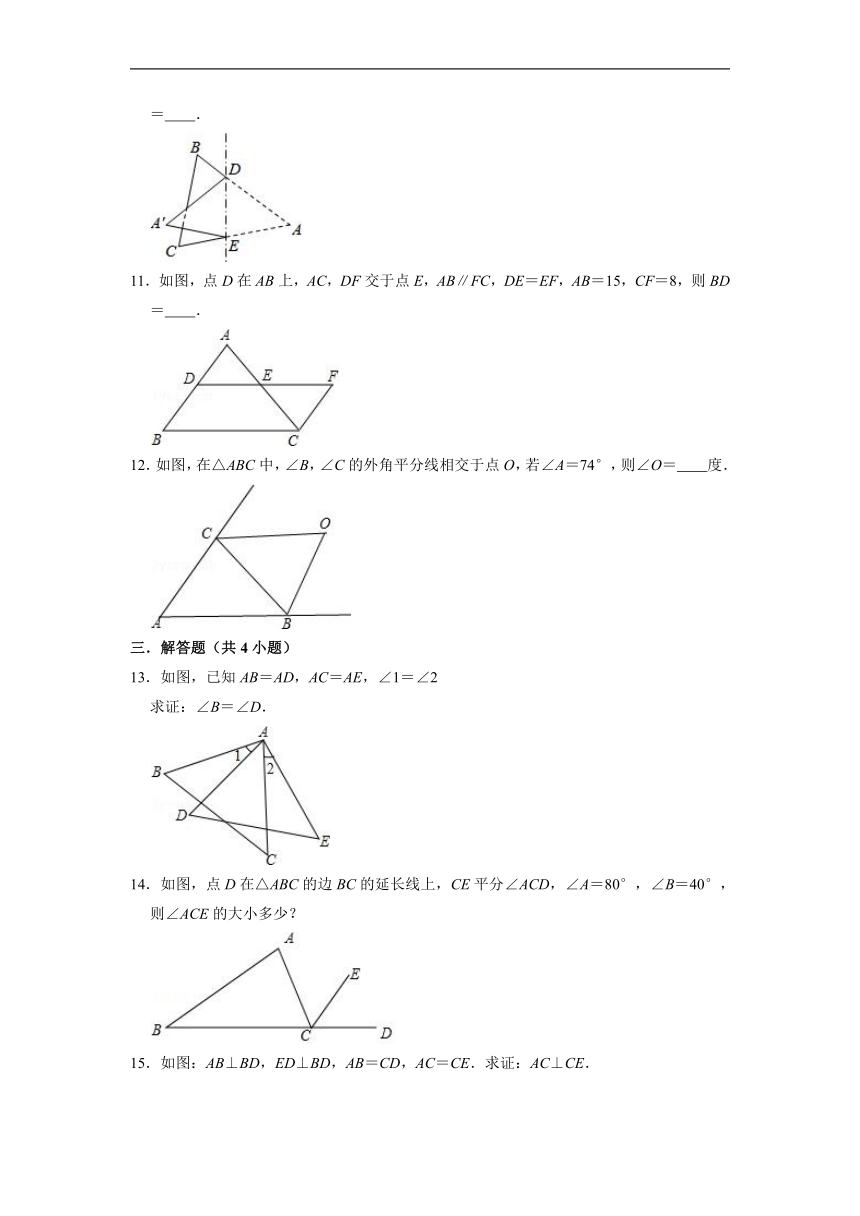
10.如图,将△ABC沿着DE对折,点A落到A′处,若∠BDA′+∠CEA′=70°,则∠A= .
11.如图,点D在AB上,AC,DF交于点E,AB∥FC,DE=EF,AB=15,CF=8,则BD= .
12.如图,在△ABC中,∠B,∠C的外角平分线相交于点O,若∠A=74°,则∠O= 度.
三.解答题(共4小题)
13.如图,已知AB=AD,AC=AE,∠1=∠2
求证:∠B=∠D.
14.如图,点D在△ABC的边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE的大小多少?
15.如图:AB⊥BD,ED⊥BD,AB=CD,AC=CE.求证:AC⊥CE.
16.如图,△ABC中,AB=BC=CA,∠A=∠ABC=∠ACB,在△ABC的顶点A,C处各有一只小蚂蚁,它们同时出发,分别以相同速度由A向B和由C向A爬行,经过t(s)后,它们分别爬行到了D,E处,设DC与BE的交点为F.
(1)证明△ACD≌△CBE;
(2)小蚂蚁在爬行过程中,DC与BE所成的∠BFC的大小有无变化?请说明理由.
参考答案与试题解析
1【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.
【解答】解:根据三角形的三边关系,知
A、1+2<4,不能组成三角形,故本选项错误;
B、2+4=6,不能够组成三角形,故本选项错误;
C、6﹣4<8<4+6,能组成三角形,故本选项正确;
D、5+6<12,不能组成三角形,故本选项错误;
故选:C.
【点评】此题考查了三角形的三边关系.判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数.
2【分析】标注字母,然后利用“边角边”求出△ABC和△DEA全等,根据全等三角形对应角相等可得∠2=∠3,再根据直角三角形两锐角互余求解.
【解答】解:如图,在△ABC和△DEA中,
,
∴△ABC≌△DEA(SAS),
∴∠2=∠3,
在Rt△ABC中,∠1+∠3=90°,
∴∠1+∠2=90°.
故选:B.
全等三角形是解题的关键.
3【分析】根据题干中给出描述可得AO=OD,BO=OC,再根据对顶角相等可得∠AOB=∠COD,即可解题.
【解答】证明:在△AOB和△COD中,
,
∴△AOB≌△COD(SAS),
∴AB=CD.
【点评】本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△AOB≌△COD是解题的关键.
4【分析】根据平行线的性质推知△AED是直角三角形;在直角△ABD中,利用“直角三角形的两个锐角互余的性质”求得∠BAD=34°;然后在直角△AED中,利用“直角三角形的两个锐角互余的性质”求得∠ADE的度数.
【解答】解:∵∠BAC=90°,DE∥AC(已知)
∴∠DEA=180°﹣∠BAC=90°(两直线平行,同旁内角互补).
∵AD⊥BC,∠B=56°,
∴∠BAD=34°,
在△ADE中,∵DE⊥AB,
∴∠ADE=56°.
故选:A.
【点评】本题考查了平行线的性质,直角三角形的性质.直角三角形的两个锐角互余.
5【分析】根据三角形的角平分线、中线和高的概念判断.
【解答】解:∵AF是△ABC的中线,
∴BF=CF,A说法正确,不符合题意;
∵AD是高,
∴∠ADC=90°,
∴∠C+∠CAD=90°,B说法正确,不符合题意;
∵AE是角平分线,
∴∠BAE=∠CAE,C说法错误,符合题意;
∵BF=CF,
∴S△ABC=2S△ABF,D说法正确,不符合题意;
故选:C.
【点评】本题考查的是三角形的角平分线、中线和高,掌握它们的概念是解题的关键 6【分析】首先根据D是BC的中点,可得:S△ABD=S△ACD=S△ABC,再根据E是AD的中点,可得:S△BDE=S△ABD,S△CDE=S△ACD,所以S△BCE=S△ABC;然后根据F是CE的中点,求出△BEF的面积是多少即可.
【解答】解:∵D是BC的中点,
∴S△ABD=S△ACD=S△ABC,
∵E是AD的中点,
∴S△BDE=S△ABD,S△CDE=S△ACD,
∴S△BCE=S△ABC=×32=16,
∵F是CE的中点,
∴S△BEF=S△BCE=×16=8.
答:图中阴影部分面积等于8.
故选:B.
【点评】此题主要考查了三角形的面积的求法,以及线段的中点的特征和应用,要熟练掌握.
7【分析】先根据三角形内角和定理求出∠A的度数,再根据CF是AB上的高得出∠ACF的度数,再由三角形外角的性质即可得出结论.
【解答】解:∵∠ABC=66°,∠ACB=54°,
∴∠A=60°,
∵CF是AB上的高,
∴在△ACF中,∠ACF=180°﹣∠AFC﹣∠A=30°,
在△CEH中,∠ACF=30°,∠CEH=90°,
∴∠EHF=∠ACF+∠CEH=30°+90°=120°.
故选:D.
【点评】本题考查的是三角形内角和定理及三角形外角的性质、三角形的高线等知识,难度适中
8【分析】先根据矩形的性质得出AD∥BC,故可得出∠DAC的度数,由角平分线的定义求出∠EAF的度数,再由EF是线段AC的垂直平分线得出∠AEF的度数,根据三角形内角和定理得出∠AFE的度数,进而可得出结论.
【解答】解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAC=∠ACB=68°.
∵由作法可知,AF是∠DAC的平分线,
∴∠EAF=∠DAC=34°.
∵由作法可知,EF是线段AC的垂直平分线,
∴∠AEF=90°,
∴∠AFE=90°﹣34°=56°,
∴∠α=56°.
故选:A.
点评】本题考查的是作图﹣基本作图,熟知角平分线及线段垂直平分线的作法是解答此题的关键.
二.填空题(共4小题
9【分析】全等三角形的判定定理有SAS,ASA,AAS,SSS,根据定理和已知条件逐个判断即可.
【解答】解:
①∠E=∠B,不符合全等三角形的判定定理,不能推出△ABC≌△DEF,∴①错误;
②ED=BC,不符合全等三角形的判定定理,不能推出△ABC≌△DEF,∴②错误;
③AB=EF,不符合全等三角形的判定定理,不能推出△ABC≌△DEF,∴③错误;
④∵AF=CD,
∴AF+FC=CD+FC,
∴AC=DF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴④正确;
故答案为:④.
【点评】本题考查了全等三角形的判定定理的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.
10【分析】根据折叠的性质得到∠A′DE=∠ADE,∠A′ED=∠AED,由平角的定义得到∠BDA′+2∠ADE=180°,∠A′EC+2∠AED=180°,根据已知条件得到∠ADE+∠AED=140°,由三角形的内角和即可得到结论.
【解答】解:∵将△ABC沿着DE对折,A落到A′,
∴∠A′DE=∠ADE,∠A′ED=∠AED,
∴∠BDA′+2∠ADE=180°,∠A′EC+2∠AED=180°,
∴∠BDA′+2∠ADE+∠A′EC+2∠AED=360°,
∵∠BDA′+∠CEA′=70°,
∴∠ADE+∠AED=145°,
∴∠A=35°.
故答案为:35°.
【点评】本题考查图形的折叠变化及三角形的内角和定理.关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.
11【分析】利用AB∥FC,可得一组内错角相等,即∠ADE=∠F,又DE=EF,再加一组对顶角,利用ASA可证△ADE≌△CFE,利用全等三角形的性质可得AD=CF,利用等量代换可求BD.
【解答】解:∵AB∥FC,
∴∠ADE=∠F
又∵DE=EF,∠AED=∠CEF,
∴△ADE≌△CFE,
∴AD=CF,
∵AB=15,CF=8,
∴BD=AB﹣AD=15﹣8=7.
故答案是:7.
【点评】本题考查了全等三角形的判定及性质,利用了平行线的性质、全等三角形的判定和性质,要熟练掌握并灵活运用.
12【分析】根据三角形的内角和定理,得∠ACB+∠ABC=180°﹣74°=106°;再根据邻补角的定义,得两个角的邻补角的和是360°﹣106°=254°;再根据角平分线的定义,得∠OCB+∠OBC=127°;最后根据三角形的内角和定理,得∠O=53°.
【解答】解:∵∠A=74°,
∴∠ACB+∠ABC=180°﹣74°=106°,
∴∠BOC=180°﹣(360°﹣106°)=180°﹣127°=53°.
【点评】此题综合运用了三角形的内角和定理以及角平分线定义.注意此题中可以总结结论:三角形的相邻两个外角的角平分线所成的锐角等于90°减去第三个内角的一半,即∠BOC=90°﹣∠A.
三.解答题(共4小题)
13【分析】根据等式的性质,可得∠BAC与∠CAE的关系,根据SAS,可得三角形全等,再根据全等三角形的性质,可得答案.
【解答】证明:∵∠1=∠2,
∴∠BAC=∠DAE,
在△BAC和△DAE中,,
∴△BAC≌△DAE (SAS),
∴∠B=∠D.
【点评】本题考查了全等三角的判定与性质,先利用了等式的性质,有利用了SAS证明三角形全等,最后利用了全等三角型的性质.
14【分析】由∠A=80°,∠B=40°,根据三角形任意一个外角等于与之不相邻的两内角的和得到∠ACD=∠B+∠A=120°,然后利用角平分线的定义计算即可.
【解答】解:∵∠ACD是△ABC的外角,
∴∠ACD=∠B+∠A=80°+40°=120°.
∵CE平分∠ACD,
∴∠ACE=∠ACD=60°.
【点评】本题考查了三角形的外角定理,关键是掌握三角形任意一个外角等于与之不相邻的两内角的和.
15【分析】由条件可证明Rt△ABC≌Rt△CDE,得到∠ECD=∠A,进一步可得∠ECA=90°,可证得结论.
【解答】证明:∵AB⊥BD,ED⊥BD,
∴∠ABC=∠CDE=90°,
在Rt△ABC和Rt△CDE中,
,
∴Rt△ABC≌Rt△CDE(HL),
∴∠A=∠ECD,
∵∠A+∠ACB=90°,
∴∠ECD+∠ACB=90°,
∴∠ACE=90°,
∴AC⊥CE.
【点评】本题主要考查直角三角形全等的判定,掌握直角三角形全等的判定方法HL定理是解题的关键
16【分析】(1)根据小蚂蚁的速度相同求出AD=CE,再利用“边角边”证明△ACD和△CBE全等即可;
(2)根据全等三角形对应角相等可得∠EBC=∠ACD,然后表示出∠BFC,再根据等边三角形的性质求出∠ACB,从而得到∠BFC.
【解答】(1)证明:∵小蚂蚁同时从A、C出发,速度相同,
∴t(s)后两只小蚂蚁爬行的路程AD=CE,
∵在△ACD和△CBE中,
,
∴△ACD≌△CBE(SAS);
(2)解:∵△ACD≌△CBE,
∴∠EBC=∠ACD,
∵∠BFC=180°﹣∠EBC﹣∠BCD,
∴∠BFC=180°﹣∠ACD﹣∠BCD,
=180°﹣∠ACB,
∵∠A=∠ABC=∠ACB,
∴∠ACB=60°,
∴∠BFC=180°﹣60°=120°,
∴∠BFC无变化.
【点评】本题考查了全等三角形的应用,主要利用了全等三角形对应角相等的性质,等边三角形的性质,根据小蚂蚁的速度相同求出AD=CE是证明三角形全等的关键.
一.选择题(共8小题)
1.以下列各组线段长为边能组成三角形的是( )
A.1cm,2cm,4cm B.2cm,4cm,6cm
C.4cm,6cm,8cm D.5cm,6cm,12cm
2.如图,在2×2的方格纸中,∠1+∠2等于( )
A.60° B.90° C.120° D.150°
3.小红家有一个小口瓶(如图所示),她很想知道它的内径是多少?但是尺子不能伸到里边直接测,于是她拿来了两根长度相同的细木条,并且把两根细木条的中点固定在一起,木条可以绕中点转动,这样只要量出AB的长,就可以知道玻璃瓶的内径是多少,那么△OAB≌△OCD理由是( )
A.边角边 B.角边角 C.边边边 D.角角边
4.如图,已知直角△ABC中,∠BAC=90°,∠B=56°,AD⊥BC,DE∥CA.∠ADE的度数为( )
A.56° B.34° C.44° D.46°
5.如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法中错误的是( )
A.BF=CF B.∠C+∠CAD=90°
C.∠BAF=∠CAF D.S△ABC=2S△ABF
6.如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且△ABC的面积是32,则图中阴影部分面积等于( )
A.16 B.8 C.4 D.2
7.在△ABC中,已知∠ABC=66°,∠ACB=54°,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,∠EHF的度数是( )
A.50° B.40° C.130° D.120°
.
8.如图,依据尺规作图的痕迹,计算∠α=( )
A.56° B.68° C.28° D.34°
二.填空题(共4小题)
9.如图,已知:∠A=∠D,∠1=∠2,下列条件中能使△ABC≌△DEF的有 .
①∠E=∠B;②ED=BC;③AB=EF;④AF=CD.
10.如图,将△ABC沿着DE对折,点A落到A′处,若∠BDA′+∠CEA′=70°,则∠A= .
11.如图,点D在AB上,AC,DF交于点E,AB∥FC,DE=EF,AB=15,CF=8,则BD= .
12.如图,在△ABC中,∠B,∠C的外角平分线相交于点O,若∠A=74°,则∠O= 度.
三.解答题(共4小题)
13.如图,已知AB=AD,AC=AE,∠1=∠2
求证:∠B=∠D.
14.如图,点D在△ABC的边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE的大小多少?
15.如图:AB⊥BD,ED⊥BD,AB=CD,AC=CE.求证:AC⊥CE.
16.如图,△ABC中,AB=BC=CA,∠A=∠ABC=∠ACB,在△ABC的顶点A,C处各有一只小蚂蚁,它们同时出发,分别以相同速度由A向B和由C向A爬行,经过t(s)后,它们分别爬行到了D,E处,设DC与BE的交点为F.
(1)证明△ACD≌△CBE;
(2)小蚂蚁在爬行过程中,DC与BE所成的∠BFC的大小有无变化?请说明理由.
参考答案与试题解析
1【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.
【解答】解:根据三角形的三边关系,知
A、1+2<4,不能组成三角形,故本选项错误;
B、2+4=6,不能够组成三角形,故本选项错误;
C、6﹣4<8<4+6,能组成三角形,故本选项正确;
D、5+6<12,不能组成三角形,故本选项错误;
故选:C.
【点评】此题考查了三角形的三边关系.判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数.
2【分析】标注字母,然后利用“边角边”求出△ABC和△DEA全等,根据全等三角形对应角相等可得∠2=∠3,再根据直角三角形两锐角互余求解.
【解答】解:如图,在△ABC和△DEA中,
,
∴△ABC≌△DEA(SAS),
∴∠2=∠3,
在Rt△ABC中,∠1+∠3=90°,
∴∠1+∠2=90°.
故选:B.
全等三角形是解题的关键.
3【分析】根据题干中给出描述可得AO=OD,BO=OC,再根据对顶角相等可得∠AOB=∠COD,即可解题.
【解答】证明:在△AOB和△COD中,
,
∴△AOB≌△COD(SAS),
∴AB=CD.
【点评】本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△AOB≌△COD是解题的关键.
4【分析】根据平行线的性质推知△AED是直角三角形;在直角△ABD中,利用“直角三角形的两个锐角互余的性质”求得∠BAD=34°;然后在直角△AED中,利用“直角三角形的两个锐角互余的性质”求得∠ADE的度数.
【解答】解:∵∠BAC=90°,DE∥AC(已知)
∴∠DEA=180°﹣∠BAC=90°(两直线平行,同旁内角互补).
∵AD⊥BC,∠B=56°,
∴∠BAD=34°,
在△ADE中,∵DE⊥AB,
∴∠ADE=56°.
故选:A.
【点评】本题考查了平行线的性质,直角三角形的性质.直角三角形的两个锐角互余.
5【分析】根据三角形的角平分线、中线和高的概念判断.
【解答】解:∵AF是△ABC的中线,
∴BF=CF,A说法正确,不符合题意;
∵AD是高,
∴∠ADC=90°,
∴∠C+∠CAD=90°,B说法正确,不符合题意;
∵AE是角平分线,
∴∠BAE=∠CAE,C说法错误,符合题意;
∵BF=CF,
∴S△ABC=2S△ABF,D说法正确,不符合题意;
故选:C.
【点评】本题考查的是三角形的角平分线、中线和高,掌握它们的概念是解题的关键 6【分析】首先根据D是BC的中点,可得:S△ABD=S△ACD=S△ABC,再根据E是AD的中点,可得:S△BDE=S△ABD,S△CDE=S△ACD,所以S△BCE=S△ABC;然后根据F是CE的中点,求出△BEF的面积是多少即可.
【解答】解:∵D是BC的中点,
∴S△ABD=S△ACD=S△ABC,
∵E是AD的中点,
∴S△BDE=S△ABD,S△CDE=S△ACD,
∴S△BCE=S△ABC=×32=16,
∵F是CE的中点,
∴S△BEF=S△BCE=×16=8.
答:图中阴影部分面积等于8.
故选:B.
【点评】此题主要考查了三角形的面积的求法,以及线段的中点的特征和应用,要熟练掌握.
7【分析】先根据三角形内角和定理求出∠A的度数,再根据CF是AB上的高得出∠ACF的度数,再由三角形外角的性质即可得出结论.
【解答】解:∵∠ABC=66°,∠ACB=54°,
∴∠A=60°,
∵CF是AB上的高,
∴在△ACF中,∠ACF=180°﹣∠AFC﹣∠A=30°,
在△CEH中,∠ACF=30°,∠CEH=90°,
∴∠EHF=∠ACF+∠CEH=30°+90°=120°.
故选:D.
【点评】本题考查的是三角形内角和定理及三角形外角的性质、三角形的高线等知识,难度适中
8【分析】先根据矩形的性质得出AD∥BC,故可得出∠DAC的度数,由角平分线的定义求出∠EAF的度数,再由EF是线段AC的垂直平分线得出∠AEF的度数,根据三角形内角和定理得出∠AFE的度数,进而可得出结论.
【解答】解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAC=∠ACB=68°.
∵由作法可知,AF是∠DAC的平分线,
∴∠EAF=∠DAC=34°.
∵由作法可知,EF是线段AC的垂直平分线,
∴∠AEF=90°,
∴∠AFE=90°﹣34°=56°,
∴∠α=56°.
故选:A.
点评】本题考查的是作图﹣基本作图,熟知角平分线及线段垂直平分线的作法是解答此题的关键.
二.填空题(共4小题
9【分析】全等三角形的判定定理有SAS,ASA,AAS,SSS,根据定理和已知条件逐个判断即可.
【解答】解:
①∠E=∠B,不符合全等三角形的判定定理,不能推出△ABC≌△DEF,∴①错误;
②ED=BC,不符合全等三角形的判定定理,不能推出△ABC≌△DEF,∴②错误;
③AB=EF,不符合全等三角形的判定定理,不能推出△ABC≌△DEF,∴③错误;
④∵AF=CD,
∴AF+FC=CD+FC,
∴AC=DF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴④正确;
故答案为:④.
【点评】本题考查了全等三角形的判定定理的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.
10【分析】根据折叠的性质得到∠A′DE=∠ADE,∠A′ED=∠AED,由平角的定义得到∠BDA′+2∠ADE=180°,∠A′EC+2∠AED=180°,根据已知条件得到∠ADE+∠AED=140°,由三角形的内角和即可得到结论.
【解答】解:∵将△ABC沿着DE对折,A落到A′,
∴∠A′DE=∠ADE,∠A′ED=∠AED,
∴∠BDA′+2∠ADE=180°,∠A′EC+2∠AED=180°,
∴∠BDA′+2∠ADE+∠A′EC+2∠AED=360°,
∵∠BDA′+∠CEA′=70°,
∴∠ADE+∠AED=145°,
∴∠A=35°.
故答案为:35°.
【点评】本题考查图形的折叠变化及三角形的内角和定理.关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.
11【分析】利用AB∥FC,可得一组内错角相等,即∠ADE=∠F,又DE=EF,再加一组对顶角,利用ASA可证△ADE≌△CFE,利用全等三角形的性质可得AD=CF,利用等量代换可求BD.
【解答】解:∵AB∥FC,
∴∠ADE=∠F
又∵DE=EF,∠AED=∠CEF,
∴△ADE≌△CFE,
∴AD=CF,
∵AB=15,CF=8,
∴BD=AB﹣AD=15﹣8=7.
故答案是:7.
【点评】本题考查了全等三角形的判定及性质,利用了平行线的性质、全等三角形的判定和性质,要熟练掌握并灵活运用.
12【分析】根据三角形的内角和定理,得∠ACB+∠ABC=180°﹣74°=106°;再根据邻补角的定义,得两个角的邻补角的和是360°﹣106°=254°;再根据角平分线的定义,得∠OCB+∠OBC=127°;最后根据三角形的内角和定理,得∠O=53°.
【解答】解:∵∠A=74°,
∴∠ACB+∠ABC=180°﹣74°=106°,
∴∠BOC=180°﹣(360°﹣106°)=180°﹣127°=53°.
【点评】此题综合运用了三角形的内角和定理以及角平分线定义.注意此题中可以总结结论:三角形的相邻两个外角的角平分线所成的锐角等于90°减去第三个内角的一半,即∠BOC=90°﹣∠A.
三.解答题(共4小题)
13【分析】根据等式的性质,可得∠BAC与∠CAE的关系,根据SAS,可得三角形全等,再根据全等三角形的性质,可得答案.
【解答】证明:∵∠1=∠2,
∴∠BAC=∠DAE,
在△BAC和△DAE中,,
∴△BAC≌△DAE (SAS),
∴∠B=∠D.
【点评】本题考查了全等三角的判定与性质,先利用了等式的性质,有利用了SAS证明三角形全等,最后利用了全等三角型的性质.
14【分析】由∠A=80°,∠B=40°,根据三角形任意一个外角等于与之不相邻的两内角的和得到∠ACD=∠B+∠A=120°,然后利用角平分线的定义计算即可.
【解答】解:∵∠ACD是△ABC的外角,
∴∠ACD=∠B+∠A=80°+40°=120°.
∵CE平分∠ACD,
∴∠ACE=∠ACD=60°.
【点评】本题考查了三角形的外角定理,关键是掌握三角形任意一个外角等于与之不相邻的两内角的和.
15【分析】由条件可证明Rt△ABC≌Rt△CDE,得到∠ECD=∠A,进一步可得∠ECA=90°,可证得结论.
【解答】证明:∵AB⊥BD,ED⊥BD,
∴∠ABC=∠CDE=90°,
在Rt△ABC和Rt△CDE中,
,
∴Rt△ABC≌Rt△CDE(HL),
∴∠A=∠ECD,
∵∠A+∠ACB=90°,
∴∠ECD+∠ACB=90°,
∴∠ACE=90°,
∴AC⊥CE.
【点评】本题主要考查直角三角形全等的判定,掌握直角三角形全等的判定方法HL定理是解题的关键
16【分析】(1)根据小蚂蚁的速度相同求出AD=CE,再利用“边角边”证明△ACD和△CBE全等即可;
(2)根据全等三角形对应角相等可得∠EBC=∠ACD,然后表示出∠BFC,再根据等边三角形的性质求出∠ACB,从而得到∠BFC.
【解答】(1)证明:∵小蚂蚁同时从A、C出发,速度相同,
∴t(s)后两只小蚂蚁爬行的路程AD=CE,
∵在△ACD和△CBE中,
,
∴△ACD≌△CBE(SAS);
(2)解:∵△ACD≌△CBE,
∴∠EBC=∠ACD,
∵∠BFC=180°﹣∠EBC﹣∠BCD,
∴∠BFC=180°﹣∠ACD﹣∠BCD,
=180°﹣∠ACB,
∵∠A=∠ABC=∠ACB,
∴∠ACB=60°,
∴∠BFC=180°﹣60°=120°,
∴∠BFC无变化.
【点评】本题考查了全等三角形的应用,主要利用了全等三角形对应角相等的性质,等边三角形的性质,根据小蚂蚁的速度相同求出AD=CE是证明三角形全等的关键.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
