2022-2023学年北师大版数学九年级上册1.1菱形的性质与判定(第一课时)课后培优练习(含解析)
文档属性
| 名称 | 2022-2023学年北师大版数学九年级上册1.1菱形的性质与判定(第一课时)课后培优练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 20:37:51 | ||
图片预览



文档简介
菱形的性质与判定(第一课时)
一、单选题
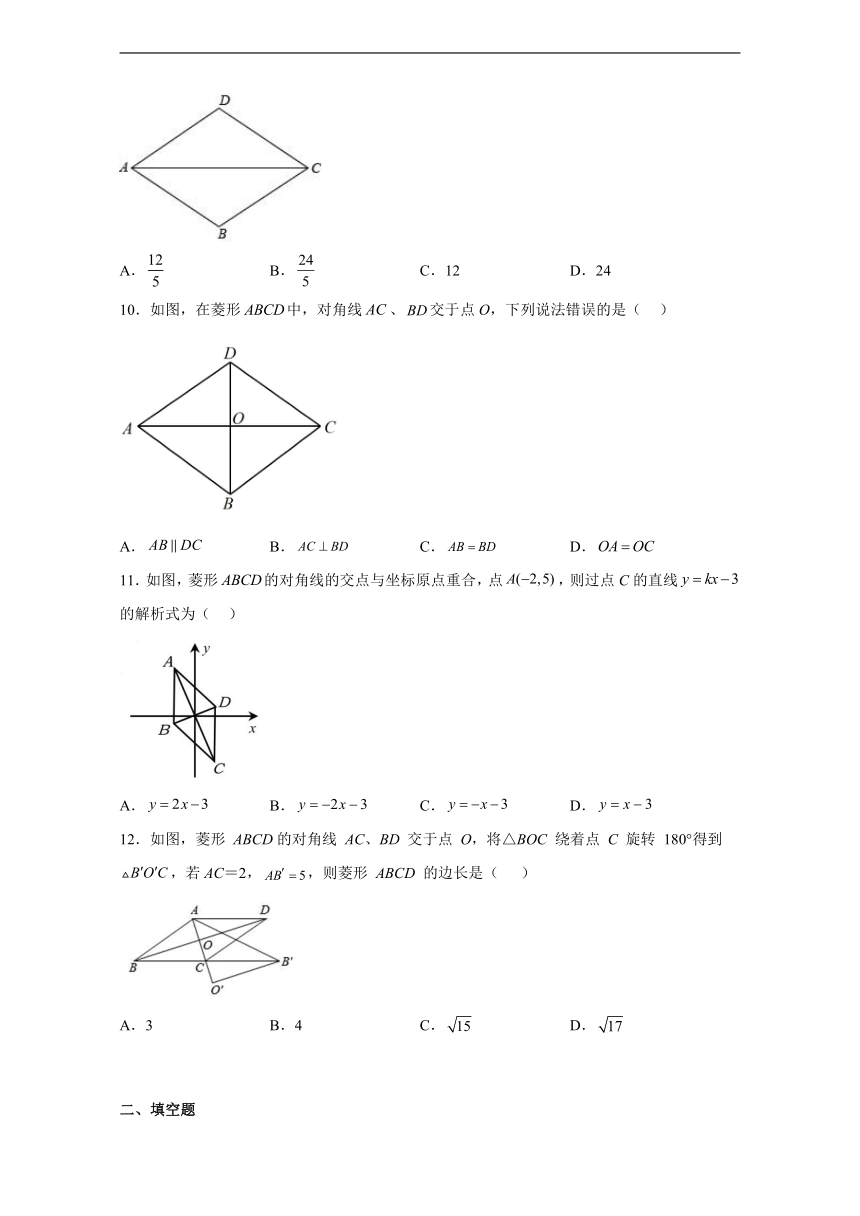
1.如图,在菱形ABCD中,对角线AC与BD.相交于点O,OE⊥AB,垂足为E,若∠ADC=130°,则∠AOE的大小为( )
A.21 B.65 C.42 D.56
2.如图,在菱形纸片ABCD中,E是BC边上一点,将△ABE沿直线AE翻折,使点B落在上,连接.已知∠C=120°,∠BAE=50°,则的度数为( )
A.50° B.60° C.80° D.90°
3.如图,平行四边形ABCD中,∠A=110°,AD=DC.E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠PEF=( )
A.35° B.45° C.50° D.55°
4.如图,菱形ABCD中,点E是AB的中点,对角线AC、BD相交于点F,连接EF,如果EF=4, 那么菱形的ABCD的周长为( )
A.4 B.8 C.16 D.32
5.如图,在平面直角坐标系中,O是菱形ABCD对角线BD的中点,ADx轴,AD=2,∠A=60°.将菱形ABCD绕点O旋转,使点D落在y轴上,则旋转后点A的对应点的坐标是( ).
A.或 B.
C. D.或
6.如图,菱形ABCD对角线AC、BD相交于点O,点E在AC上,,,,则DE的长为( )
A. B. C. D.
7.菱形的两条对角线分别是6cm,8 cm,则菱形面积为( )
A. B. C. D.
8.如图,菱形ABCD的对角线长分别为6和8,点P是对角线AC上任意一点(不与点A,C重合),PE//BC交AB于点E,PF//CD交AD于点F,则阴影部分的面积是( )
A.12 B.11 C.10 D.24
9.如图,在菱形ABCD中,AB=5,AC=8,则菱形的高为( )
A. B. C.12 D.24
10.如图,在菱形中,对角线、交于点O,下列说法错误的是( )
A. B. C. D.
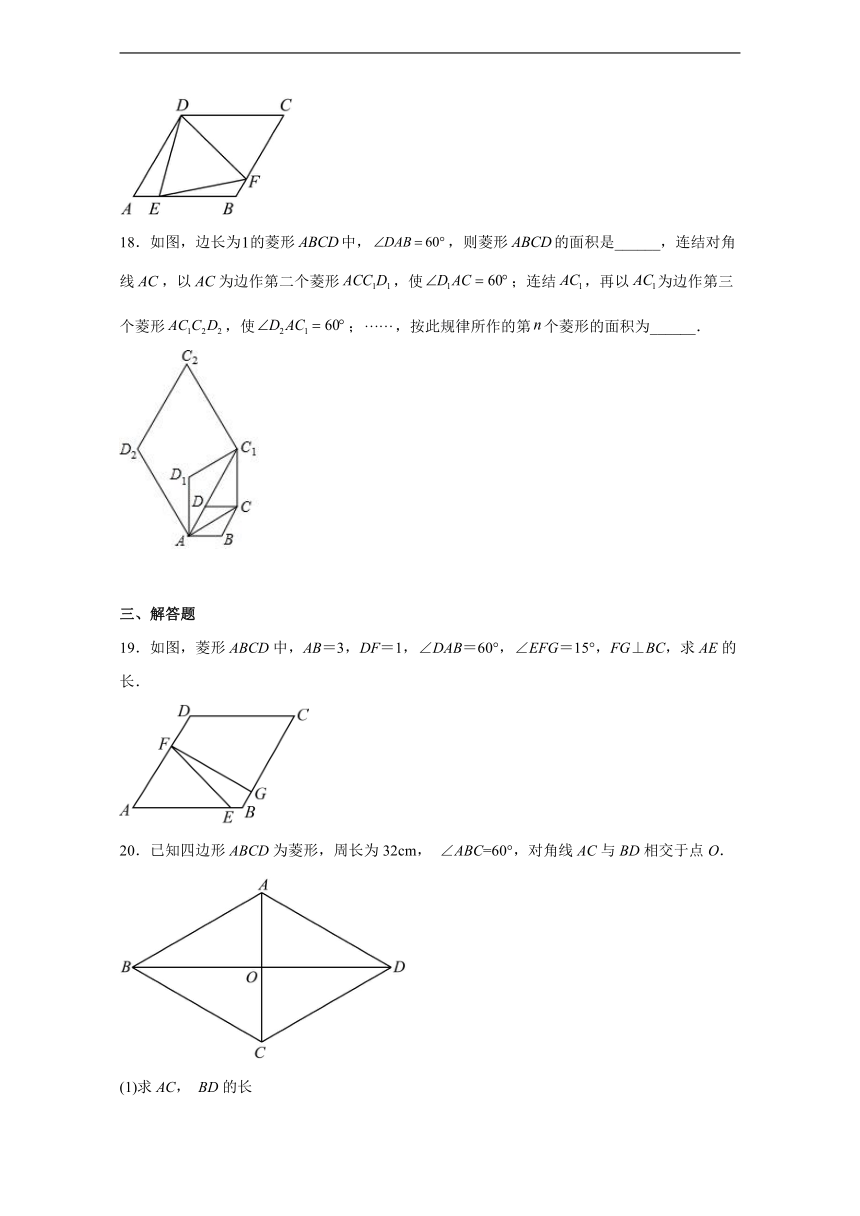
11.如图,菱形的对角线的交点与坐标原点重合,点,则过点C的直线的解析式为( )
A. B. C. D.
12.如图,菱形 ABCD的对角线 AC、BD 交于点 O,将△BOC 绕着点 C 旋转 180°得到,若AC=2,,则菱形 ABCD 的边长是( )
A.3 B.4 C. D.
二、填空题
13.在菱形ABCD中,∠C=120°,点E是AD边的中点,点P是对角线BD上的动点,则当PA+PE的值最小时,∠APB=_____.
14.如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=35°,则∠OBC的大小为_____度.
15.如图,在菱形ABCD中,AB的垂直平分线EF交对角线AC于点F,垂足为点E,连接DF,且∠CDF=18°,则∠DAF=___ 度.
16.如图,菱形的一边中点到对角线交点的距离为,则菱形周长为______.
17.如图所示,在菱形中,,E,F两点分别从A,B两点同时出发,以相同的速度分别向终点B,C移动,连接,在移动的过程中,的最小值为____________.
18.如图,边长为的菱形中,,则菱形的面积是______,连结对角线,以为边作第二个菱形,使;连结,再以为边作第三个菱形,使;,按此规律所作的第个菱形的面积为______.
三、解答题
19.如图,菱形ABCD中,AB=3,DF=1,∠DAB=60°,∠EFG=15°,FG⊥BC,求AE的长.
20.已知四边形ABCD为菱形,周长为32cm, ∠ABC=60°,对角线AC与BD相交于点O.
(1)求AC, BD的长
(2)求菱形ABCD的面积
21.如图,在菱形ABCD中,AB的垂直平分线交对角线AC于点F,交AB于点E,连接DF,BF.
(1)求证:;
(2)若∠ADC=110°,求的度数.
22.在菱形中,,点是射线上一动点,以为边向右侧作等边,点的位置随着点的位置变化而变化.
(1)问题发现如图,当点在菱形内部或边上时,连接,与的数量关系是______;与的位置关系是______;
(2)拓展探究
如图,当点在菱形外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由;
(3)解决问题
如图,若,,请直接写出四边形的面积.
参考答案:
1.B
解:在菱形ABCD中,∠ADC=130°,
∴∠BAD=180°﹣130°=50°,
∴∠BAO=∠BAD=×50°=25°,
∵OE⊥AB,
∴∠AOE=90°﹣∠BAO=90°﹣25°=65°.
故选:B.
2.C
解:∵四边形ABCD是菱形,∠C=120°,
∴∠BAD=∠C=120°,AB=AD,
∵将△ABE沿直线AE翻折,使点B落在上,
∴∠BAE==50°,=AB,
∴=100°,=AD,
∴=20°,
∴==(180°-20°)÷2=80°,
故选:C.
3.A
解:∵平行四边形ABCD中,AD=DC,
∴四边形ABCD为菱形,
∴AB=BC,∠ABC=180°-∠A=70°,
∵E,F分别为AB,BC的中点,
∴BE=BF,
∴ ,
∵PE⊥CD,AB∥CD,
∴PE⊥AB,
∴∠PEB=90°,
∴ ,
故选:A.
4.D
解:∵菱形ABCD中,对角线AC和BD交于点F,
∴AF=CF,
∵E是AB的中点,
∴EF是三角形ABC的中位线,
∴EF=BC,
∴BC=2EF=2×4=8.即AB=BC=CD=AD=8.
故菱形的周长为4BC=4×8=32.
故选:D.
5.A
解:根据菱形的对称性可得:当点D旋转到y轴正半轴时,
A、B、C均在坐标轴上,如下图,
∵∠BAD=60°,AD=2,
∴∠OAD=30°,
∴OD=1,
∴AO=OD==OC,
∴点A的坐标为(,0);
同理:当点D旋转到y轴负半轴时,此时点A旋转到x轴正半轴,
点A的坐标为(,0),
∴点A的坐标为(,0)或(-,0),
故选:A.
6.A
解:∵四边形ABCD为菱形,
∴,,
在中,,
∵,
∴,
在中,,
故选:A.
7.B
解:∵菱形的两条对角线分别是6cm,8 cm,
∴菱形面积为.
故选:B
8.A
解:设AP与EF相交于O点.
∵四边形ABCD为菱形,
∴BC//AD,AB//CD.
∵PE//BC,PF//CD,
∴PE//AF,PF//AE.
∴四边形AEPF是平行四边形.
∴S△POF=S△AOE.
∴阴影部分的面积就是△ABC的面积,
∴△ABC的面积=菱形的面积=×(×6×8)=12,
则阴影部分的面积是12.
故选:A.
9.B
解:设AC与BD交于点O,作出BC边的高h,
∵四边形ABCD是菱形,
∴AO⊥BO,且AC=2AO,BD=2BO.
在Rt△AOB中利用勾股定理可得BO==3.
∴BD=2BO=6.
∴菱形的面积为BD×AC=×6×8=24.
设BC变上的高为h,则BC×h=24,
即5h=24,
解得:h=,
故选:B.
10.C
解:A、菱形的对边平行且相等,所以,故该选项正确;
B、菱形的对角线一定垂直,所以AC⊥BD,故该选项正确;
C、菱形的对角线不一定与边相等,所以AB与BD不一定相等,故该选项错误;
D、菱形的对角线互相平分,所以OA=OC,故该选项正确.
故选:C.
11.C
解:菱形的对角线的交点与坐标原点重合,点
由直线过点C,
,故C正确,符合题意,
故选:C
12.D
解:∵四边形ABCD是菱形,且△BOC绕着点C旋转180°得到,,
∴,,,
∴,,
∵,
∴,
∴,
∴,即菱形 ABCD 的边长是.
故选:D.
13.60°##60度
解:如图,连接AC,CE,AC交BD于点O,
∵四边形ABCD是菱形,
∴,AO=CO,,AB=BC=CD=AD,,
∴AP=CP,
∵∠BCD=120°,
∴∠ADC=∠ABC=60°,
∴△ABC和△ACD都是等边三角形,
又∵点E为AD的中点,
∴CE⊥AD,
∵CP+PE≥CE,AP=CP,
∴当C,P,E三点共线时,PA+PE的值最小,等于CE的长,
此时,∠ADP=∠DAP=30°,
∴∠APB=30°+30°=60°.
故答案为:60°.
14.55°
解:∵四边形ABCD是菱形,
∴∠BAC=∠DAC=∠DCA=∠BCA=35°,AB=BC,
在△AOM和△CON中,
,
∴△AOM≌△CON,
∴OA=OC,
∵AB=BC,
∴OB⊥AC,
∴∠OBC=90°-∠BCA=90°-35°=55°,
故答案为:55°.
15.54
解:连接BD,BF,
∵四边形ABCD是菱形,
∴AD=CD,
∴∠DAC=∠DCA.
∵EF垂直平分AB,AC垂直平分BD,
∴AF=BF,BF=DF,
∴AF=DF,
∴∠DAF=∠FDA,
∵∠DAF+∠ADF+∠DCA+∠CDF=180°,
∴3∠DAF+∠CDF=180°,
∵∠CDF=18°,
∴3∠DAF+18°=180°,
则∠DAF=54°,
故答案为:54.
16.
解:点菱形的边的中点,点是的中点,且,
∴在中,,
∴,
故菱形的周长是.
故答案为:12.
17.
解:连接DB,作DH⊥AB于H,如图,
∵四边形ABCD为菱形,
∴AD=AB=BC=CD,
而∠A=60°,
∴△ABD和△BCD都是等边三角形,
∴∠ADB=∠DBC=60°,AD=BD,
在Rt△ADH中,AH=1,AD=2,
∴DH==,
在△ADE和△BDF中,
∴△ADE≌△BDF,
∴∠2=∠1,DE=DF,
∴∠1+∠BDE=∠2+∠BDE=∠EDF=60°,
∴△DEF为等边三角形,
∴EF=DE,
而当E点运动到H点时,DE的值最小,其最小值为,
∴EF的最小值为,
故答案为:.
18.
解:如图,连接BD,交AC与点O,
∵四边形ABCD为菱形,且∠DAB=60°,
∴△ABD为等边三角形,
∴AD=BD=AB=1,
∴BO,AO,
∴S△ABD,
∴S菱形ABCD=2.
∵AO,
∴AC,
∵四边形ACC1D1为菱形,∠D1AC=60°,
∴可得AC,
同理可得AC2AC1,
以此类推,可得出所作的第n个菱形的边长为,
∴第n个菱形的面积为2.
故答案为:;.
19.1+
解:过FH⊥AB,垂足为H.
∵四边形ABCD是菱形,
∴AD=AB=3,
∵DF=1,
∴AF=AD-FD=2,
∵∠DAB=60°,
∴∠AFH=30°,
∴AH=1,FH=,
又∵∠EFG=15°,
∴∠EFH=∠AFG-∠AFH-∠EFG=90°-30°-15°=45°,
∴△FHE是等腰直角三角形,
∴HE=FH=,
∴AE=AH+HE=1+.
20.(1)AC=8cm,BD=8cm;
(2)菱形ABCD的面积为32.
(1)
解:∵菱形ABCD的周长为32cm,∠ABC=60°,
∴AB=BC=8cm,△ABC是等边三角形,AC、BD互相垂直平分,
∴AC=AB=8cm,OA=AC=4cm,OB=OD,
∴OB=(cm),
∴BD=8cm;
(2)
解:菱形ABCD的面积=AC BD=×8×8=32().
21.(1)见解析
(2)∠FDC=75°.
(1)
证明:连接BF,如图所示:
∵EF是线段AB的垂直平分线,
∴AF=BF,
∵四边形ABCD是菱形,
∴BC=DC,∠BCF=∠DCF,
在△BCF和△DCF中,
,
∴△BCF≌△DCF(SAS),
∴BF=DF,
∴AF=DF;
(2)
解:∵四边形ABCD是菱形,∠ADC=110°,
∴AD=DC,∠DCA=∠DAC=(180°-∠ADC)=×70°=35°,
∵AF=DF,
∴∠FDA=∠DAC=35°,
∴∠DFC=∠FDA+∠DAC=70°,
∴∠FDC=180°-∠DFC-∠DCA=180°-70°-35°=75°.
22.(1);
(2)成立,证明见解析
(3)
(1)
解:如图,连接,延长交于,
菱形中,,
,,
、是等边三角形,
,,,
是等边三角形,
,,
,即,
在与中,,
,
,,
平分,
,
,
,
.
故答案为:,.
(2)
解:成立,,,证明如下:
如图,连接,
菱形中,,
,,
、是等边三角形,
,,,
是等边三角形,
,,
,即,
在与中,,
,
,,
平分,
,
平分,
.
(3)
解:由(2)知,,,
,,
,
四边形的面积为.
一、单选题
1.如图,在菱形ABCD中,对角线AC与BD.相交于点O,OE⊥AB,垂足为E,若∠ADC=130°,则∠AOE的大小为( )
A.21 B.65 C.42 D.56
2.如图,在菱形纸片ABCD中,E是BC边上一点,将△ABE沿直线AE翻折,使点B落在上,连接.已知∠C=120°,∠BAE=50°,则的度数为( )
A.50° B.60° C.80° D.90°
3.如图,平行四边形ABCD中,∠A=110°,AD=DC.E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠PEF=( )
A.35° B.45° C.50° D.55°
4.如图,菱形ABCD中,点E是AB的中点,对角线AC、BD相交于点F,连接EF,如果EF=4, 那么菱形的ABCD的周长为( )
A.4 B.8 C.16 D.32
5.如图,在平面直角坐标系中,O是菱形ABCD对角线BD的中点,ADx轴,AD=2,∠A=60°.将菱形ABCD绕点O旋转,使点D落在y轴上,则旋转后点A的对应点的坐标是( ).
A.或 B.
C. D.或
6.如图,菱形ABCD对角线AC、BD相交于点O,点E在AC上,,,,则DE的长为( )
A. B. C. D.
7.菱形的两条对角线分别是6cm,8 cm,则菱形面积为( )
A. B. C. D.
8.如图,菱形ABCD的对角线长分别为6和8,点P是对角线AC上任意一点(不与点A,C重合),PE//BC交AB于点E,PF//CD交AD于点F,则阴影部分的面积是( )
A.12 B.11 C.10 D.24
9.如图,在菱形ABCD中,AB=5,AC=8,则菱形的高为( )
A. B. C.12 D.24
10.如图,在菱形中,对角线、交于点O,下列说法错误的是( )
A. B. C. D.
11.如图,菱形的对角线的交点与坐标原点重合,点,则过点C的直线的解析式为( )
A. B. C. D.
12.如图,菱形 ABCD的对角线 AC、BD 交于点 O,将△BOC 绕着点 C 旋转 180°得到,若AC=2,,则菱形 ABCD 的边长是( )
A.3 B.4 C. D.
二、填空题
13.在菱形ABCD中,∠C=120°,点E是AD边的中点,点P是对角线BD上的动点,则当PA+PE的值最小时,∠APB=_____.
14.如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=35°,则∠OBC的大小为_____度.
15.如图,在菱形ABCD中,AB的垂直平分线EF交对角线AC于点F,垂足为点E,连接DF,且∠CDF=18°,则∠DAF=___ 度.
16.如图,菱形的一边中点到对角线交点的距离为,则菱形周长为______.
17.如图所示,在菱形中,,E,F两点分别从A,B两点同时出发,以相同的速度分别向终点B,C移动,连接,在移动的过程中,的最小值为____________.
18.如图,边长为的菱形中,,则菱形的面积是______,连结对角线,以为边作第二个菱形,使;连结,再以为边作第三个菱形,使;,按此规律所作的第个菱形的面积为______.
三、解答题
19.如图,菱形ABCD中,AB=3,DF=1,∠DAB=60°,∠EFG=15°,FG⊥BC,求AE的长.
20.已知四边形ABCD为菱形,周长为32cm, ∠ABC=60°,对角线AC与BD相交于点O.
(1)求AC, BD的长
(2)求菱形ABCD的面积
21.如图,在菱形ABCD中,AB的垂直平分线交对角线AC于点F,交AB于点E,连接DF,BF.
(1)求证:;
(2)若∠ADC=110°,求的度数.
22.在菱形中,,点是射线上一动点,以为边向右侧作等边,点的位置随着点的位置变化而变化.
(1)问题发现如图,当点在菱形内部或边上时,连接,与的数量关系是______;与的位置关系是______;
(2)拓展探究
如图,当点在菱形外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由;
(3)解决问题
如图,若,,请直接写出四边形的面积.
参考答案:
1.B
解:在菱形ABCD中,∠ADC=130°,
∴∠BAD=180°﹣130°=50°,
∴∠BAO=∠BAD=×50°=25°,
∵OE⊥AB,
∴∠AOE=90°﹣∠BAO=90°﹣25°=65°.
故选:B.
2.C
解:∵四边形ABCD是菱形,∠C=120°,
∴∠BAD=∠C=120°,AB=AD,
∵将△ABE沿直线AE翻折,使点B落在上,
∴∠BAE==50°,=AB,
∴=100°,=AD,
∴=20°,
∴==(180°-20°)÷2=80°,
故选:C.
3.A
解:∵平行四边形ABCD中,AD=DC,
∴四边形ABCD为菱形,
∴AB=BC,∠ABC=180°-∠A=70°,
∵E,F分别为AB,BC的中点,
∴BE=BF,
∴ ,
∵PE⊥CD,AB∥CD,
∴PE⊥AB,
∴∠PEB=90°,
∴ ,
故选:A.
4.D
解:∵菱形ABCD中,对角线AC和BD交于点F,
∴AF=CF,
∵E是AB的中点,
∴EF是三角形ABC的中位线,
∴EF=BC,
∴BC=2EF=2×4=8.即AB=BC=CD=AD=8.
故菱形的周长为4BC=4×8=32.
故选:D.
5.A
解:根据菱形的对称性可得:当点D旋转到y轴正半轴时,
A、B、C均在坐标轴上,如下图,
∵∠BAD=60°,AD=2,
∴∠OAD=30°,
∴OD=1,
∴AO=OD==OC,
∴点A的坐标为(,0);
同理:当点D旋转到y轴负半轴时,此时点A旋转到x轴正半轴,
点A的坐标为(,0),
∴点A的坐标为(,0)或(-,0),
故选:A.
6.A
解:∵四边形ABCD为菱形,
∴,,
在中,,
∵,
∴,
在中,,
故选:A.
7.B
解:∵菱形的两条对角线分别是6cm,8 cm,
∴菱形面积为.
故选:B
8.A
解:设AP与EF相交于O点.
∵四边形ABCD为菱形,
∴BC//AD,AB//CD.
∵PE//BC,PF//CD,
∴PE//AF,PF//AE.
∴四边形AEPF是平行四边形.
∴S△POF=S△AOE.
∴阴影部分的面积就是△ABC的面积,
∴△ABC的面积=菱形的面积=×(×6×8)=12,
则阴影部分的面积是12.
故选:A.
9.B
解:设AC与BD交于点O,作出BC边的高h,
∵四边形ABCD是菱形,
∴AO⊥BO,且AC=2AO,BD=2BO.
在Rt△AOB中利用勾股定理可得BO==3.
∴BD=2BO=6.
∴菱形的面积为BD×AC=×6×8=24.
设BC变上的高为h,则BC×h=24,
即5h=24,
解得:h=,
故选:B.
10.C
解:A、菱形的对边平行且相等,所以,故该选项正确;
B、菱形的对角线一定垂直,所以AC⊥BD,故该选项正确;
C、菱形的对角线不一定与边相等,所以AB与BD不一定相等,故该选项错误;
D、菱形的对角线互相平分,所以OA=OC,故该选项正确.
故选:C.
11.C
解:菱形的对角线的交点与坐标原点重合,点
由直线过点C,
,故C正确,符合题意,
故选:C
12.D
解:∵四边形ABCD是菱形,且△BOC绕着点C旋转180°得到,,
∴,,,
∴,,
∵,
∴,
∴,
∴,即菱形 ABCD 的边长是.
故选:D.
13.60°##60度
解:如图,连接AC,CE,AC交BD于点O,
∵四边形ABCD是菱形,
∴,AO=CO,,AB=BC=CD=AD,,
∴AP=CP,
∵∠BCD=120°,
∴∠ADC=∠ABC=60°,
∴△ABC和△ACD都是等边三角形,
又∵点E为AD的中点,
∴CE⊥AD,
∵CP+PE≥CE,AP=CP,
∴当C,P,E三点共线时,PA+PE的值最小,等于CE的长,
此时,∠ADP=∠DAP=30°,
∴∠APB=30°+30°=60°.
故答案为:60°.
14.55°
解:∵四边形ABCD是菱形,
∴∠BAC=∠DAC=∠DCA=∠BCA=35°,AB=BC,
在△AOM和△CON中,
,
∴△AOM≌△CON,
∴OA=OC,
∵AB=BC,
∴OB⊥AC,
∴∠OBC=90°-∠BCA=90°-35°=55°,
故答案为:55°.
15.54
解:连接BD,BF,
∵四边形ABCD是菱形,
∴AD=CD,
∴∠DAC=∠DCA.
∵EF垂直平分AB,AC垂直平分BD,
∴AF=BF,BF=DF,
∴AF=DF,
∴∠DAF=∠FDA,
∵∠DAF+∠ADF+∠DCA+∠CDF=180°,
∴3∠DAF+∠CDF=180°,
∵∠CDF=18°,
∴3∠DAF+18°=180°,
则∠DAF=54°,
故答案为:54.
16.
解:点菱形的边的中点,点是的中点,且,
∴在中,,
∴,
故菱形的周长是.
故答案为:12.
17.
解:连接DB,作DH⊥AB于H,如图,
∵四边形ABCD为菱形,
∴AD=AB=BC=CD,
而∠A=60°,
∴△ABD和△BCD都是等边三角形,
∴∠ADB=∠DBC=60°,AD=BD,
在Rt△ADH中,AH=1,AD=2,
∴DH==,
在△ADE和△BDF中,
∴△ADE≌△BDF,
∴∠2=∠1,DE=DF,
∴∠1+∠BDE=∠2+∠BDE=∠EDF=60°,
∴△DEF为等边三角形,
∴EF=DE,
而当E点运动到H点时,DE的值最小,其最小值为,
∴EF的最小值为,
故答案为:.
18.
解:如图,连接BD,交AC与点O,
∵四边形ABCD为菱形,且∠DAB=60°,
∴△ABD为等边三角形,
∴AD=BD=AB=1,
∴BO,AO,
∴S△ABD,
∴S菱形ABCD=2.
∵AO,
∴AC,
∵四边形ACC1D1为菱形,∠D1AC=60°,
∴可得AC,
同理可得AC2AC1,
以此类推,可得出所作的第n个菱形的边长为,
∴第n个菱形的面积为2.
故答案为:;.
19.1+
解:过FH⊥AB,垂足为H.
∵四边形ABCD是菱形,
∴AD=AB=3,
∵DF=1,
∴AF=AD-FD=2,
∵∠DAB=60°,
∴∠AFH=30°,
∴AH=1,FH=,
又∵∠EFG=15°,
∴∠EFH=∠AFG-∠AFH-∠EFG=90°-30°-15°=45°,
∴△FHE是等腰直角三角形,
∴HE=FH=,
∴AE=AH+HE=1+.
20.(1)AC=8cm,BD=8cm;
(2)菱形ABCD的面积为32.
(1)
解:∵菱形ABCD的周长为32cm,∠ABC=60°,
∴AB=BC=8cm,△ABC是等边三角形,AC、BD互相垂直平分,
∴AC=AB=8cm,OA=AC=4cm,OB=OD,
∴OB=(cm),
∴BD=8cm;
(2)
解:菱形ABCD的面积=AC BD=×8×8=32().
21.(1)见解析
(2)∠FDC=75°.
(1)
证明:连接BF,如图所示:
∵EF是线段AB的垂直平分线,
∴AF=BF,
∵四边形ABCD是菱形,
∴BC=DC,∠BCF=∠DCF,
在△BCF和△DCF中,
,
∴△BCF≌△DCF(SAS),
∴BF=DF,
∴AF=DF;
(2)
解:∵四边形ABCD是菱形,∠ADC=110°,
∴AD=DC,∠DCA=∠DAC=(180°-∠ADC)=×70°=35°,
∵AF=DF,
∴∠FDA=∠DAC=35°,
∴∠DFC=∠FDA+∠DAC=70°,
∴∠FDC=180°-∠DFC-∠DCA=180°-70°-35°=75°.
22.(1);
(2)成立,证明见解析
(3)
(1)
解:如图,连接,延长交于,
菱形中,,
,,
、是等边三角形,
,,,
是等边三角形,
,,
,即,
在与中,,
,
,,
平分,
,
,
,
.
故答案为:,.
(2)
解:成立,,,证明如下:
如图,连接,
菱形中,,
,,
、是等边三角形,
,,,
是等边三角形,
,,
,即,
在与中,,
,
,,
平分,
,
平分,
.
(3)
解:由(2)知,,,
,,
,
四边形的面积为.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
