2022-2023学年北师大版数学九年级上册1.2矩形的性质与判定(第一课时)课后培优练习(含解析)
文档属性
| 名称 | 2022-2023学年北师大版数学九年级上册1.2矩形的性质与判定(第一课时)课后培优练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 20:35:47 | ||
图片预览


文档简介
矩形的性质与判定(第一课时)
一、单选题
1.如图是叠放在一起的两张长方形卡片,则图中相等的是( )
A.∠1与∠2 B.∠2与∠3 C.∠1与∠3 D.三个角都相等
2.下列性质中,矩形具有而菱形不一定具有的是( )
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.邻边相等
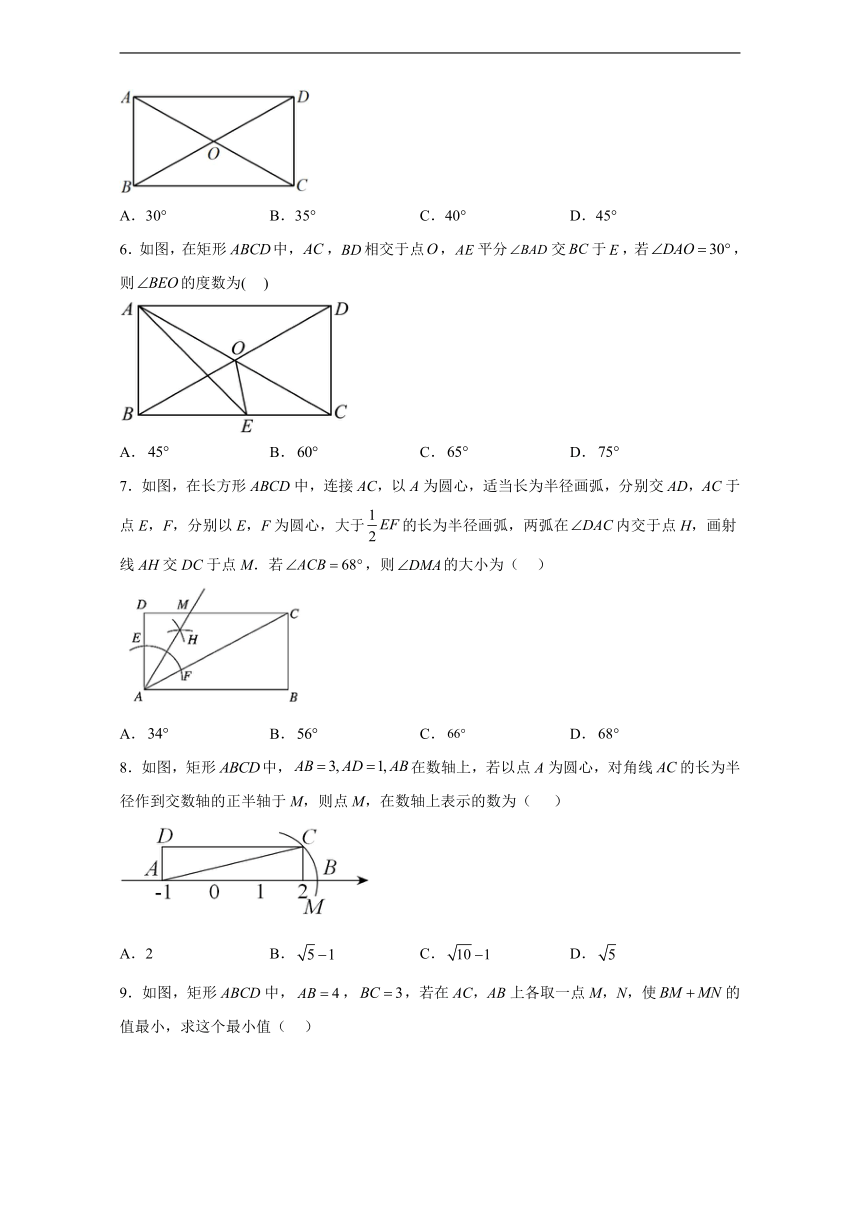
3.如图,在矩形中,,,过对角线交点作交于点,交于点,则的长是( )
A. B. C.1 D.
4.如图,在长方形ABCD中AB=CD=4,AD=BC=5.延长BC到E,使CE=2,连接DE,动点P从点B出发,以每秒4个单位的速度沿BC-CD-DA向终点A运动,设点P运动的时间为t秒,存在这样的t,使△ABP和△DCE全等,则t的值为( )
A.t= B.t=2 C.t=或t=2 D.t=或t=3
5.如图,在矩形中,对角线,交于点O.若,则的度数为( )
A.30° B.35° C.40° D.45°
6.如图,在矩形中,,相交于点,平分交于,若,则的度数为( )
A. B. C. D.
7.如图,在长方形ABCD中,连接AC,以A为圆心,适当长为半径画弧,分别交AD,AC于点E,F,分别以E,F为圆心,大于的长为半径画弧,两弧在内交于点H,画射线AH交DC于点M.若,则的大小为( )
A. B. C. D.
8.如图,矩形中,在数轴上,若以点A为圆心,对角线的长为半径作到交数轴的正半轴于M,则点M,在数轴上表示的数为( )
A.2 B. C. D.
9.如图,矩形ABCD中,,,若在AC,AB上各取一点M,N,使的值最小,求这个最小值( )
A. B. C. D.
10.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD面积的( )
A. B. C. D.
11.如图,矩形的面积为5,它的两条对角线交于点,以为两邻边作平行四边形,平行四边形的对角线交于点,同样以为两邻边作平行四边形,…,依此类推,则平行四边形的面积为( )
A. B. C. D.
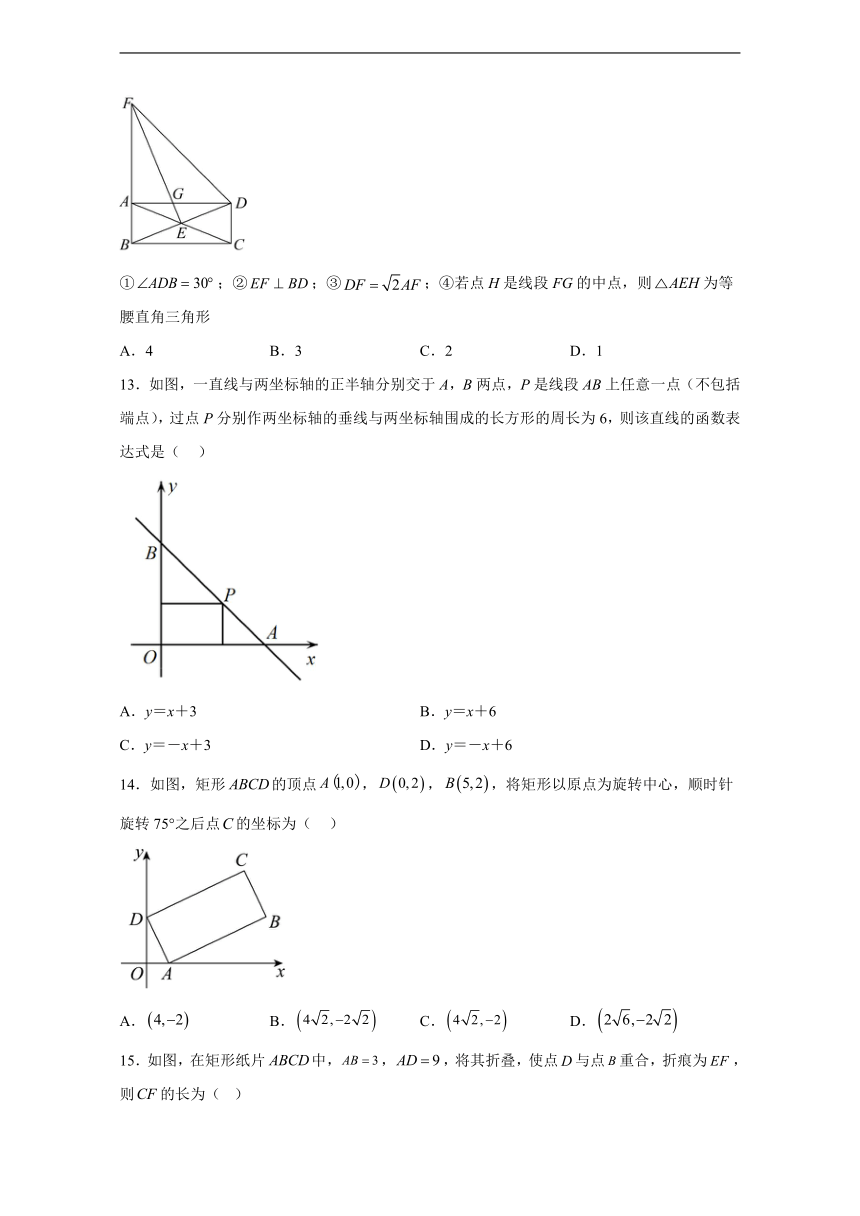
12.如图,矩形ABCD的对角线相交于点E,延长BA至点F,使.此时,连接EF,交AD于点G,则下列结论中正确的个数是( )
①;②;③;④若点H是线段FG的中点,则为等腰直角三角形
A.4 B.3 C.2 D.1
13.如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线与两坐标轴围成的长方形的周长为6,则该直线的函数表达式是( )
A.y=x+3 B.y=x+6
C.y=-x+3 D.y=-x+6
14.如图,矩形的顶点,,,将矩形以原点为旋转中心,顺时针旋转75°之后点的坐标为( )
A. B. C. D.
15.如图,在矩形纸片中,,,将其折叠,使点与点重合,折痕为,则的长为( )
A.4 B.5 C. D.3.5
二、填空题
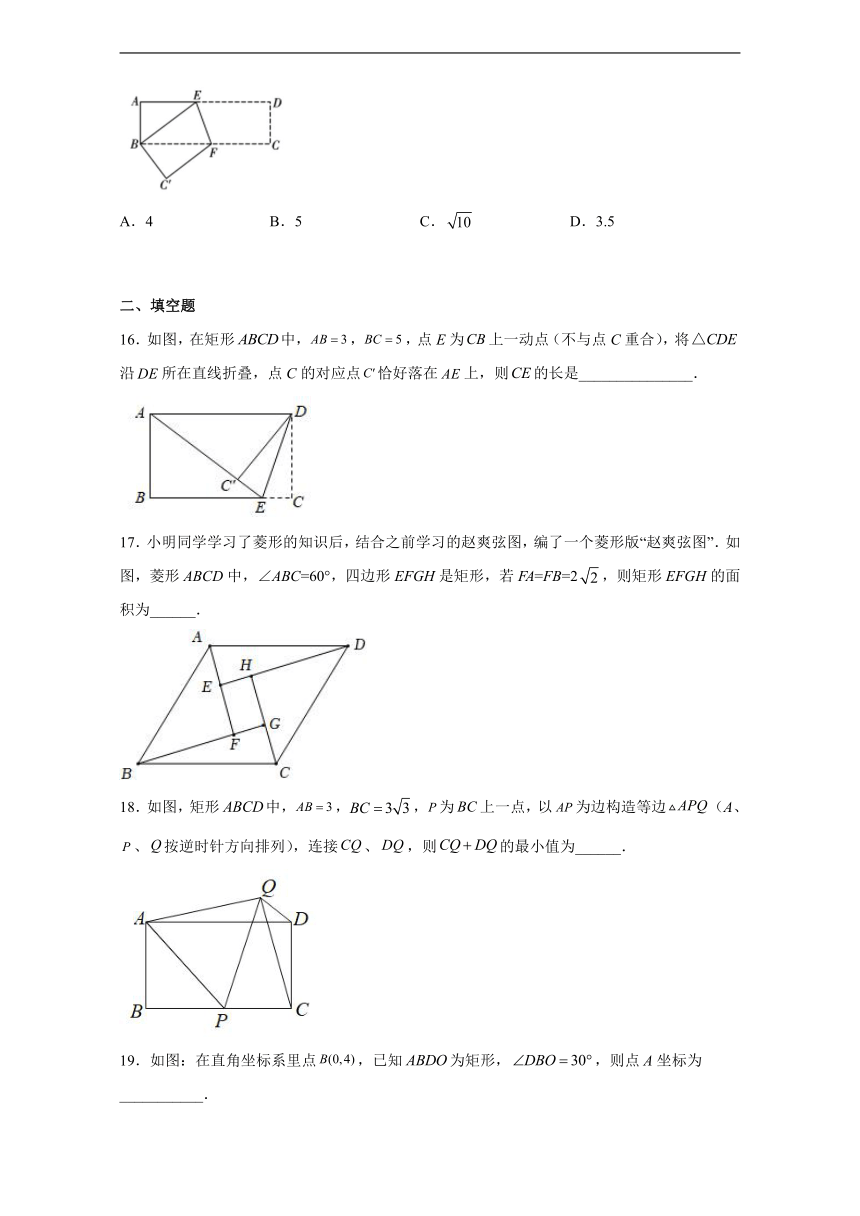
16.如图,在矩形中,,,点E为上一动点(不与点C重合),将沿所在直线折叠,点C的对应点恰好落在上,则的长是_______________.
17.小明同学学习了菱形的知识后,结合之前学习的赵爽弦图,编了一个菱形版“赵爽弦图”.如图,菱形ABCD中,∠ABC=60°,四边形EFGH是矩形,若FA=FB=2,则矩形EFGH的面积为______.
18.如图,矩形中,,,为上一点,以为边构造等边(A、、按逆时针方向排列),连接、,则的最小值为______.
19.如图:在直角坐标系里点,已知为矩形,,则点A坐标为___________.
20.在研究平面图形的面积时,我们经常用到割补法.割补法在我国古代数学著作中称为“出入相补”,刘徽称之为“以盈补虚”,即以多余补不足,是数量的平均思想在几何上的体现.九章算术已经能十分灵活地应用“出入相补”原理解决平面图形的面积问题.下面举例说明:在九章算术中,三角形被称为圭田.圭田术曰:“半广以乘正纵”,也就是说三角形的面积等于底的一半乘高.刘徽注为:“半广者,以盈补虚,为直田也”,说明三角形的面积是应用出入相补原理,由长方形面积导出的.如图中的三角形下盈上虚,以下补上.如果图中阴影部分的面积为,那么图中长方形的面积是______.
21.如图,在矩形ABCD中,对角线AC、BD相交于点O,点F为BC上一点,将沿DF翻折,点C的对应点恰好是点O,连接AF,若,则AF的长为______.
三、解答题
22.如图,在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,求DE的长
23.如图,四边形ABCD是矩形,AB=2,AD=4,点E、F分别在AD、BC上,且AE=CF,连接BD、EF.
(1)求证:四边形BFDE是平行四边形;
(2)若EF⊥BD,求AE的长度.
24.如图,在矩形ABCD中,对角线AC的垂直平分线分别与边AB和边CD的延长线交于点M,N,与边AD交于点E,垂足为点O.
(1)求证:△AOM≌△CON;
(2)若AB=4,AD=8,求AE的长.
25.已知矩形ABCD中,AB=3,BC=4,E为直线BC上一点.
(1)如图1,当E在线段BC上,且DE=AD时,求BE的长;
(2)如图2,点E为BC边延长线上一点,若BD=BE,连接DE,M为DE的中点,连接AM、CM,求证:AM⊥CM.
26.如图,在矩形ABCD中,AE平分∠BAD交BC于点E,点F为AE上一点,连接BF,CF,满足BF=CF,AE=AD,延长BF交DE于点G,连接DF.
(1)求证:AB=AF.
(2)求证:EG=DG.
(3)若EG=2,求矩形ABCD的面积.
27.在□ABCD中,∠ADC的平分线交BC于点E,交AB的延长线于点F,以BE,BF为邻边作.
(1)如图1,求证:是菱形;
(2)如图2,若,连接BG,交EF于点O,连接OA,OC,AC,求OA的长;
(3)如图3,若,连接AC,AG,求∠GAC的度数.
参考答案:
1.B
解:连接GH,如图所示:
∵两张长方形卡片叠放在一起,
∴∠C=∠D=∠A=∠B=∠AEF,
∵∠CEG+∠DEF=90°,∠CEG+∠CGE=90°,
∴∠CGE=∠DEF,
∵∠3+∠CGE=180°,∠1+∠DFE=180°,
∴∠1与∠3的大小无法判定;
∵∠AHG=∠BHK,∠AGH+∠AHG=90°,∠BHK+∠BKH=90°,
∴∠AGH=∠BKH,
∵∠3+∠AGH=180°,∠2+∠BKH=180°,
∴∠2=∠3.
故选:B.
2.A
解:矩形的性质有:①矩形的对边平行且相等,②矩形的四个角都是直角,③矩形的对角线互相平分且相等;
菱形的性质有:①菱形的对边平行,菱形的四条边都相等,②菱形的对角相等,③菱形的对角线互相平分且垂直,并且每一条对角线平分一组对角,
所以矩形具有而菱形不一定具有的性质是对角线相等,
故选:A.
3.A
解:如图,连接,
∵四边形是矩形,
∴,,,,
又∵,
∴线段是线段的垂直平分线,
∴,
设,则,
在中,
∵,
∴,
解得:,
∴.
故选:A
4.D
解:∵四边形ABCD是矩形,
∴∠ABP=∠BAD=∠BCD=90°,
∴∠DCE=90°,
分两种情况:
①点P在BC上时,
∵AB=CD,
∴当BP=CE=2时,△ABP≌△DCE(SAS),
由题意得:BP=4t=2,
∴t=;
②点P在AD上时,
∵AB=CD,
∴当AP=CE=2时,△BAP≌△DCE(SAS),
由题意得:AP=5+4+5-4t=2,
解得:t=3;
综上所述,当t的值为或3时,△ABP和△DCE全等,
故选:D.
5.A
解:∵四边形ABCD是矩,∠AOB=60°,
∴∠BCD=90°,∠COD=60°,OC=OD=,
∴△COD是等边三角形,
∴∠OCD=60°,
∴∠OCB=90°﹣∠OCD=30°,
故选:A.
6.D
解:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,OA=AC,OB=BD,AC=BD,
∴OA=OB,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵∠DAO=30°,
∴∠EAO=15°,
∴∠BAO=45°+15°=60°,
∴△AOB是等边三角形,
∴∠ABO=60°,OB=AB,
∴∠OBE=90°-60°=30°,OB=BE,
∴∠BEO=×(180°-30°)=75°.
故选:D.
7.B
解:四边形是长方形,
,
,
由题意可知,平分,
,
,
故选:B.
8.C
解:∵矩形中,,,
∴,,
∴,
∴,
∵A点表示-1,
∴M点表示的数为:
故选:C.
9.D
解:如图,作点B关于AC的对称点H,连接HB,交AC于O,连接AH,HM,连接HN,
∴AB=AH=4,HM=BM,BO=HO,
∴MN+BM=HM+MN,
∴当点H,点M,点N共线且HN⊥AB时,MN+BM的最小值为HN,
∵AB=4,BC=3,
∴AC=,
∵S△ABC=×AB×BC=AC×BO,
∴BO=,
∴BH=,
在中,
,
∵HN⊥AB,
S△ABH=×AB×HN=BH×AO,
∴MN+BM的最小值为.
故选:D.
10.C
解:∵四边形为矩形,
∴OB=OD=OA=OC,
在△EBO与△FDO中,
∵,
∴△EBO≌△FDO(ASA),
∴阴影部分的面积=,
∵△AOB与△ABC同底且△AOB的高是△ABC高的一半,
∴ .
故选:C.
11.B
解:矩形的面积为5,
的面积为,
四边形是平行四边形,
平行四边形的面积为,
同理可得:平行四边形的面积为,
平行四边形的面积为,
归纳类推得:平行四边形的面积为,其中为正整数,
故选:B.
12.B
解:①∵四边形ABCD是矩形,
∴∠BAD=90°,
∴∠FAD=90°,
∵AF=AD,
∴∠AFD=∠FDA=45°,
∵FB=FD,
∴∠FBD=∠FDB=67.5°,
∴∠ADB=67.5﹣45=22.5°,故①错误;
②∵四边形ABCD是矩形,
∴BE=DE,
∵BF=FD,
∴FE⊥BD,故②正确;
③∵四边形ABCD是矩形,
∴∠FAD=90°,
∵AF=AD,
∴∠AFD=∠FDA=45°,
∴,
∴DF=AF,故③正确;
④如图,
∵H是FG的中点,∠FAG=90°,
∴FH=GH=AH,
∴∠AFH=∠FAH.
∵∠AFD=45°,FE平分∠AFD,
∴∠AFH=∠FAH=22.5°,
∴∠AHG=45°,
∵四边形ABCD是矩形,
∴EA=ED,
∴∠EAD=∠EDA=22.5°,
∴∠AEB=45°,
∴∠AEG=45°,
∴∠AEG=∠AHG=45°,
∴△AEG为等腰直角三角形,故④正确.
故选:B.
13.C
解:设过点P的垂线在x轴、y轴上垂足分别是D、C,如图:
设P点坐标为(x,y),
∵P点在第一象限,
∴PD=y,PC=x,
∵矩形PDOC的周长为6,
∴2(x+y)=6,
∴x+y=3,
即该直线的函数表达式是y=﹣x+3,
故选:C.
14.D
解:过点B作BG⊥x轴于G,过点C作CH⊥y轴于H,
∵四边形ABCD是矩形,
∴AD=BC,AB=CD,ADBC,∠CDA=∠DAB=90°,
∴∠HCD=∠ADO=∠BAG,
∵∠CHD=∠BGA=90°,
∴△CHD≌△AGB(AAS),
∵,,,
∴CH=AG=5-1=4,DH=BG=2,
∴OH=2+2=4,
∴C(4,4),
∴OE=CE=4,
∴∠COE=45°,OC=4,
如图,过点C作CE⊥x轴于E,过点C1作C1F⊥x轴于F,
由旋转得∠COC1=75°,
∴∠C1OF=30°,
∴C1F=OC1=OC=2,
∴OF=,
∴点C1的坐标为,
故选:D.
15.A
解:∵四边形ABCD是矩形,
∴∠A=90°,
由翻折的性质可知,、、=90°
设=,则BF=9-x,
∵在Rt△中,
∴解得,
∴CF=4.
故选:A.
16.1
解:∵四边形ABCD是矩形,
∴∠B=∠C=90°,AD=BC=5,CD=AB=3,
由折叠的性质得:,,,
∴,
∴,
设,
在Rt△ABE中,BE=5-x,AE=x+4,
由勾股定理得:,
解得:x=1,
故答案为:1.
17.##
解:过点A作AM⊥BC于M,过点G作GN⊥BC于N,连接GM,
∵四边形EFGH是矩形,
∴∠AFB=∠AED=∠BGC=∠CHD=90°,
∵FA=FB=2,
∴AB==4,∠ABF=∠BAF=45°,
∵四边形ABCD是菱形,∠ABC=60°,
∴AB=BC=CD=AD,∠ABC=∠ADC=60°,∠BAD=∠BCD=120°,
∴∠CBG=15°,∠DAF=75°,
∴∠CDH=∠DCH=45°,∠ADE=15°,∠BCG=75°,
∴∠BAF=∠DCH=∠ABF=∠CDH,∠ADE=∠CBG,∠DAE=∠BCG,
在△ABF和△CDH中,
,
∴△ABF≌△CDH(ASA),
同理:△BCG≌△DAE(ASA),
∵AM⊥BC,∠ABC=60°,
∴∠BAM=30°,
∴BM=AB=2,
∴AM=BM=2,BC=2BM,
∵∠BGC=90°,
∴BM=CM=GM=2,
∴∠CMG=2∠CBG=30°,
∵GN⊥BC,
∴GN=GM=1,
∴S菱形ABCD=BC AM=4×2=8,
S△ABF=AF BF=×2×2=4,
S△BCG=BC GN=×4×1=2,
∴S矩形EFGH=S菱形ABCD-2S△ABF-2S△BCG=8-12.
故答案为:8-12.
18.
解:如图,连接AC,取AC的中点O,连接BO,OQ,
∵矩形ABCD中,AB=3,AD=BC=,
∴,
∵点O是AC的中点,∠ABC=90°,
∴AO=BO=CO=3,
∴AB=AO=BO=3,
∴△ABO是等边三角形,
∴∠BAO=60°,
∵△APQ是等边三角形,
∴AP=AQ,∠PAQ=∠BAO=60°,
∴∠BAP=∠QAC,
在△ABP和△AOQ中,
∴△ABP≌△AOQ(SAS),
∴∠ABP=∠AOQ=90°,
∴OQ是AC的垂直平分线,
∴AQ=CQ,
∵CQ+DQ=AQ+QD,
∴当点A,点Q,点D三点共线时,CQ+DQ的最小值为AD长,
∴CQ+DQ的最小值为,
故答案为:.
19.
解:过点A作AC⊥y轴于点C,
∵,
∴.
∵四边形为矩形
∴AM=BM=DM=,
∴,,
∴
∴△ABM是等边三角形.
又∵AC⊥y轴,
∴CM,
∴,
∴点A坐标为.
故答案为:.
20.16
解:如图,连接,
则阴影部分的面积,
图中长方形的面积是,
故答案为:.
21.
解:由翻折可得CD=OD,∠CDF=∠BDF,
∵四边形ABCD为矩形,
∴OC=OD,AB=CD,AD=BC=3,∠BCD=∠ABC=90°,
∴OC=OD=CD,
即△OCD为等边三角形,
∴∠BDC=60°,
∴CDBC,∠CDF=∠BDF=30°,
∴CFCD=1,
∴BF=BC﹣CF=2,
在Rt△ABF中,由勾股定理可得,
AF.
故答案为:.
22.3
解:如图,连接,
四边形是矩形,且,
,
,
垂直平分,
,
设,则,
在中,,即,
解得,
即.
23.(1)见解析 (2)
(1)
证明:∵四边形ABCD是矩形,
∴AD=BC,ADBC,
∵AE=CF,
∴DE=BF,DEBF,
∴四边形BFDE是平行四边形;
(2)
解:∵四边形BFDE是平行四边形,EF⊥BD,
∴四边形BFDE是菱形,
∴DE=BE,
∵四边形ABCD是矩形,
∴∠A=90°,
在Rt△ABE中,BE=DE=AD-AE=4-AE,AB=2,
根据勾股定理得:BE2=AE2+AB2,
∴(4-AE)2=AE2+22,
解得AE=.
24.(1)见解析 (2)5
(1)
证明:∵四边形ABCD是矩形,
∴ABCD,
∴∠M=∠N,
∵AC的垂直平分线是MN,
∴AO=CO,
在△AOM和△CON中,
,
∴△AOM≌△CON(AAS);
(2)
解:连接CE,设AE=x,则DE=8﹣x,
∵AC的垂直平分线是MN,
∴AE=CE=x,
∵四边形ABCD是矩形,AB=4,
∴DC=AB=4,∠ADC=90°,
由勾股定理得:,
∴,
解得:x=5,
即AE=5.
25.(1) (2)见解析
(1)
解:如图1所示,
∵四边形ABCD是矩形,
∴∠C=90°,CD=AB=3,AD=BC=4,
∴DE=AD=4,
在Rt△CDE中,CE,
∴BE=BC﹣CE=4;
(2)
如图2,连接BM,
∵点M是DE的中点,
∴DM=EM,
∵BD=BE,
∴△BDE是等腰三角形,
∴BM⊥DE,
∴∠BMD=90°,
∵四边形ABCD是矩形,
∴∠BCD=∠ADC=90°,AD=BC,
∴∠DCE=180°-∠BCD=90°,
∴△CDE是直角三角形,
∵M为DE的中点,
∴DM=CM,
∴∠CDM=∠DCM,
∴∠BCD+∠DCM=∠CDM+∠ADC,
∴∠ADM=∠BCM,
在△ADM和△BCM中,
,
∴△ADM≌△BCM(SAS).
∴∠AMD=∠BMC,
∴∠AMC=∠AMB+∠BMC=∠AMB+∠AMD=∠BMD=90°,
∴AM⊥CM;
26.(1)见解析
(2)见解析
(3)8+8
(1)
证明:∵四边形ABCD为矩形,
∴ADBC,∠DAB=∠ABE=90°,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴∠BAE=∠AEB=45°,
∴AB=EB,
∵四边形ABCD为矩形,
∴∠ABC=∠BCD=90°,AB=CD,
∵BF=CF,
∴∠FBC=∠FCB,
∴∠ABF=∠DCF,
在△ABF和△AFD中,
∴△ABF≌△AFD(SAS),
∴AF=DF,
∴∠ADF=∠DAE=45°,
∴∠AFD=90°,
∴∠ABE=∠AFD=90°,
∵AE=AD,
在△ABE和△AFD中,
∴△ABE≌△AFD(AAS),
∴AB=AF;
(2)
证明:∵AE=AD,∠EAD=45°,
∴∠AED=∠ADE=67.5°,
∴∠FDG=22.5°,
∵AB=AF,∠BAF=45°,
∴∠AFB=67.5°,
∴∠EFG=67.5°,
∴∠EFG=∠AED,
∴FG=EG,
∵∠AFD=90°,
∴∠DFE=90°,
∵∠EFG=67.5°,
∴∠DFG=∠DFE-∠EFG =22.5°,
∴∠DFG=∠FDG,
∴FG=DG,
∴EG=DG;
(3)
解:∵EG=2,
∴ED=4,
设AB=BE=x,
则AD=AE=x,DF=AF=AB=x,
∴EF=x﹣x,
∴,
∴x2=8+4,
∴.
27.(1)证明见解析
(2)
(3)∠CAG=60°
(1)
证明:四边形是平行四边形,
,,
,,
平分,
,
,
,
又四边形是平行四边形,
是菱形;
(2)
解:,
四边形是矩形,
,
,
,
菱形是正方形,
,,,
,
,
,
,
,
,
,,
,
,
;
(3)
解:如图3,延长,,交于点,连接,
四边形是平行四边形,,
,,,
四边形是菱形,
,,,
,,
四边形是平行四边形,四边形是平行四边形,,
,
,
,
四边形是菱形,
,,
是等边三角形,是等边三角形,
,,
,
,
.
一、单选题
1.如图是叠放在一起的两张长方形卡片,则图中相等的是( )
A.∠1与∠2 B.∠2与∠3 C.∠1与∠3 D.三个角都相等
2.下列性质中,矩形具有而菱形不一定具有的是( )
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.邻边相等
3.如图,在矩形中,,,过对角线交点作交于点,交于点,则的长是( )
A. B. C.1 D.
4.如图,在长方形ABCD中AB=CD=4,AD=BC=5.延长BC到E,使CE=2,连接DE,动点P从点B出发,以每秒4个单位的速度沿BC-CD-DA向终点A运动,设点P运动的时间为t秒,存在这样的t,使△ABP和△DCE全等,则t的值为( )
A.t= B.t=2 C.t=或t=2 D.t=或t=3
5.如图,在矩形中,对角线,交于点O.若,则的度数为( )
A.30° B.35° C.40° D.45°
6.如图,在矩形中,,相交于点,平分交于,若,则的度数为( )
A. B. C. D.
7.如图,在长方形ABCD中,连接AC,以A为圆心,适当长为半径画弧,分别交AD,AC于点E,F,分别以E,F为圆心,大于的长为半径画弧,两弧在内交于点H,画射线AH交DC于点M.若,则的大小为( )
A. B. C. D.
8.如图,矩形中,在数轴上,若以点A为圆心,对角线的长为半径作到交数轴的正半轴于M,则点M,在数轴上表示的数为( )
A.2 B. C. D.
9.如图,矩形ABCD中,,,若在AC,AB上各取一点M,N,使的值最小,求这个最小值( )
A. B. C. D.
10.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD面积的( )
A. B. C. D.
11.如图,矩形的面积为5,它的两条对角线交于点,以为两邻边作平行四边形,平行四边形的对角线交于点,同样以为两邻边作平行四边形,…,依此类推,则平行四边形的面积为( )
A. B. C. D.
12.如图,矩形ABCD的对角线相交于点E,延长BA至点F,使.此时,连接EF,交AD于点G,则下列结论中正确的个数是( )
①;②;③;④若点H是线段FG的中点,则为等腰直角三角形
A.4 B.3 C.2 D.1
13.如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线与两坐标轴围成的长方形的周长为6,则该直线的函数表达式是( )
A.y=x+3 B.y=x+6
C.y=-x+3 D.y=-x+6
14.如图,矩形的顶点,,,将矩形以原点为旋转中心,顺时针旋转75°之后点的坐标为( )
A. B. C. D.
15.如图,在矩形纸片中,,,将其折叠,使点与点重合,折痕为,则的长为( )
A.4 B.5 C. D.3.5
二、填空题
16.如图,在矩形中,,,点E为上一动点(不与点C重合),将沿所在直线折叠,点C的对应点恰好落在上,则的长是_______________.
17.小明同学学习了菱形的知识后,结合之前学习的赵爽弦图,编了一个菱形版“赵爽弦图”.如图,菱形ABCD中,∠ABC=60°,四边形EFGH是矩形,若FA=FB=2,则矩形EFGH的面积为______.
18.如图,矩形中,,,为上一点,以为边构造等边(A、、按逆时针方向排列),连接、,则的最小值为______.
19.如图:在直角坐标系里点,已知为矩形,,则点A坐标为___________.
20.在研究平面图形的面积时,我们经常用到割补法.割补法在我国古代数学著作中称为“出入相补”,刘徽称之为“以盈补虚”,即以多余补不足,是数量的平均思想在几何上的体现.九章算术已经能十分灵活地应用“出入相补”原理解决平面图形的面积问题.下面举例说明:在九章算术中,三角形被称为圭田.圭田术曰:“半广以乘正纵”,也就是说三角形的面积等于底的一半乘高.刘徽注为:“半广者,以盈补虚,为直田也”,说明三角形的面积是应用出入相补原理,由长方形面积导出的.如图中的三角形下盈上虚,以下补上.如果图中阴影部分的面积为,那么图中长方形的面积是______.
21.如图,在矩形ABCD中,对角线AC、BD相交于点O,点F为BC上一点,将沿DF翻折,点C的对应点恰好是点O,连接AF,若,则AF的长为______.
三、解答题
22.如图,在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,求DE的长
23.如图,四边形ABCD是矩形,AB=2,AD=4,点E、F分别在AD、BC上,且AE=CF,连接BD、EF.
(1)求证:四边形BFDE是平行四边形;
(2)若EF⊥BD,求AE的长度.
24.如图,在矩形ABCD中,对角线AC的垂直平分线分别与边AB和边CD的延长线交于点M,N,与边AD交于点E,垂足为点O.
(1)求证:△AOM≌△CON;
(2)若AB=4,AD=8,求AE的长.
25.已知矩形ABCD中,AB=3,BC=4,E为直线BC上一点.
(1)如图1,当E在线段BC上,且DE=AD时,求BE的长;
(2)如图2,点E为BC边延长线上一点,若BD=BE,连接DE,M为DE的中点,连接AM、CM,求证:AM⊥CM.
26.如图,在矩形ABCD中,AE平分∠BAD交BC于点E,点F为AE上一点,连接BF,CF,满足BF=CF,AE=AD,延长BF交DE于点G,连接DF.
(1)求证:AB=AF.
(2)求证:EG=DG.
(3)若EG=2,求矩形ABCD的面积.
27.在□ABCD中,∠ADC的平分线交BC于点E,交AB的延长线于点F,以BE,BF为邻边作.
(1)如图1,求证:是菱形;
(2)如图2,若,连接BG,交EF于点O,连接OA,OC,AC,求OA的长;
(3)如图3,若,连接AC,AG,求∠GAC的度数.
参考答案:
1.B
解:连接GH,如图所示:
∵两张长方形卡片叠放在一起,
∴∠C=∠D=∠A=∠B=∠AEF,
∵∠CEG+∠DEF=90°,∠CEG+∠CGE=90°,
∴∠CGE=∠DEF,
∵∠3+∠CGE=180°,∠1+∠DFE=180°,
∴∠1与∠3的大小无法判定;
∵∠AHG=∠BHK,∠AGH+∠AHG=90°,∠BHK+∠BKH=90°,
∴∠AGH=∠BKH,
∵∠3+∠AGH=180°,∠2+∠BKH=180°,
∴∠2=∠3.
故选:B.
2.A
解:矩形的性质有:①矩形的对边平行且相等,②矩形的四个角都是直角,③矩形的对角线互相平分且相等;
菱形的性质有:①菱形的对边平行,菱形的四条边都相等,②菱形的对角相等,③菱形的对角线互相平分且垂直,并且每一条对角线平分一组对角,
所以矩形具有而菱形不一定具有的性质是对角线相等,
故选:A.
3.A
解:如图,连接,
∵四边形是矩形,
∴,,,,
又∵,
∴线段是线段的垂直平分线,
∴,
设,则,
在中,
∵,
∴,
解得:,
∴.
故选:A
4.D
解:∵四边形ABCD是矩形,
∴∠ABP=∠BAD=∠BCD=90°,
∴∠DCE=90°,
分两种情况:
①点P在BC上时,
∵AB=CD,
∴当BP=CE=2时,△ABP≌△DCE(SAS),
由题意得:BP=4t=2,
∴t=;
②点P在AD上时,
∵AB=CD,
∴当AP=CE=2时,△BAP≌△DCE(SAS),
由题意得:AP=5+4+5-4t=2,
解得:t=3;
综上所述,当t的值为或3时,△ABP和△DCE全等,
故选:D.
5.A
解:∵四边形ABCD是矩,∠AOB=60°,
∴∠BCD=90°,∠COD=60°,OC=OD=,
∴△COD是等边三角形,
∴∠OCD=60°,
∴∠OCB=90°﹣∠OCD=30°,
故选:A.
6.D
解:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,OA=AC,OB=BD,AC=BD,
∴OA=OB,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵∠DAO=30°,
∴∠EAO=15°,
∴∠BAO=45°+15°=60°,
∴△AOB是等边三角形,
∴∠ABO=60°,OB=AB,
∴∠OBE=90°-60°=30°,OB=BE,
∴∠BEO=×(180°-30°)=75°.
故选:D.
7.B
解:四边形是长方形,
,
,
由题意可知,平分,
,
,
故选:B.
8.C
解:∵矩形中,,,
∴,,
∴,
∴,
∵A点表示-1,
∴M点表示的数为:
故选:C.
9.D
解:如图,作点B关于AC的对称点H,连接HB,交AC于O,连接AH,HM,连接HN,
∴AB=AH=4,HM=BM,BO=HO,
∴MN+BM=HM+MN,
∴当点H,点M,点N共线且HN⊥AB时,MN+BM的最小值为HN,
∵AB=4,BC=3,
∴AC=,
∵S△ABC=×AB×BC=AC×BO,
∴BO=,
∴BH=,
在中,
,
∵HN⊥AB,
S△ABH=×AB×HN=BH×AO,
∴MN+BM的最小值为.
故选:D.
10.C
解:∵四边形为矩形,
∴OB=OD=OA=OC,
在△EBO与△FDO中,
∵,
∴△EBO≌△FDO(ASA),
∴阴影部分的面积=,
∵△AOB与△ABC同底且△AOB的高是△ABC高的一半,
∴ .
故选:C.
11.B
解:矩形的面积为5,
的面积为,
四边形是平行四边形,
平行四边形的面积为,
同理可得:平行四边形的面积为,
平行四边形的面积为,
归纳类推得:平行四边形的面积为,其中为正整数,
故选:B.
12.B
解:①∵四边形ABCD是矩形,
∴∠BAD=90°,
∴∠FAD=90°,
∵AF=AD,
∴∠AFD=∠FDA=45°,
∵FB=FD,
∴∠FBD=∠FDB=67.5°,
∴∠ADB=67.5﹣45=22.5°,故①错误;
②∵四边形ABCD是矩形,
∴BE=DE,
∵BF=FD,
∴FE⊥BD,故②正确;
③∵四边形ABCD是矩形,
∴∠FAD=90°,
∵AF=AD,
∴∠AFD=∠FDA=45°,
∴,
∴DF=AF,故③正确;
④如图,
∵H是FG的中点,∠FAG=90°,
∴FH=GH=AH,
∴∠AFH=∠FAH.
∵∠AFD=45°,FE平分∠AFD,
∴∠AFH=∠FAH=22.5°,
∴∠AHG=45°,
∵四边形ABCD是矩形,
∴EA=ED,
∴∠EAD=∠EDA=22.5°,
∴∠AEB=45°,
∴∠AEG=45°,
∴∠AEG=∠AHG=45°,
∴△AEG为等腰直角三角形,故④正确.
故选:B.
13.C
解:设过点P的垂线在x轴、y轴上垂足分别是D、C,如图:
设P点坐标为(x,y),
∵P点在第一象限,
∴PD=y,PC=x,
∵矩形PDOC的周长为6,
∴2(x+y)=6,
∴x+y=3,
即该直线的函数表达式是y=﹣x+3,
故选:C.
14.D
解:过点B作BG⊥x轴于G,过点C作CH⊥y轴于H,
∵四边形ABCD是矩形,
∴AD=BC,AB=CD,ADBC,∠CDA=∠DAB=90°,
∴∠HCD=∠ADO=∠BAG,
∵∠CHD=∠BGA=90°,
∴△CHD≌△AGB(AAS),
∵,,,
∴CH=AG=5-1=4,DH=BG=2,
∴OH=2+2=4,
∴C(4,4),
∴OE=CE=4,
∴∠COE=45°,OC=4,
如图,过点C作CE⊥x轴于E,过点C1作C1F⊥x轴于F,
由旋转得∠COC1=75°,
∴∠C1OF=30°,
∴C1F=OC1=OC=2,
∴OF=,
∴点C1的坐标为,
故选:D.
15.A
解:∵四边形ABCD是矩形,
∴∠A=90°,
由翻折的性质可知,、、=90°
设=,则BF=9-x,
∵在Rt△中,
∴解得,
∴CF=4.
故选:A.
16.1
解:∵四边形ABCD是矩形,
∴∠B=∠C=90°,AD=BC=5,CD=AB=3,
由折叠的性质得:,,,
∴,
∴,
设,
在Rt△ABE中,BE=5-x,AE=x+4,
由勾股定理得:,
解得:x=1,
故答案为:1.
17.##
解:过点A作AM⊥BC于M,过点G作GN⊥BC于N,连接GM,
∵四边形EFGH是矩形,
∴∠AFB=∠AED=∠BGC=∠CHD=90°,
∵FA=FB=2,
∴AB==4,∠ABF=∠BAF=45°,
∵四边形ABCD是菱形,∠ABC=60°,
∴AB=BC=CD=AD,∠ABC=∠ADC=60°,∠BAD=∠BCD=120°,
∴∠CBG=15°,∠DAF=75°,
∴∠CDH=∠DCH=45°,∠ADE=15°,∠BCG=75°,
∴∠BAF=∠DCH=∠ABF=∠CDH,∠ADE=∠CBG,∠DAE=∠BCG,
在△ABF和△CDH中,
,
∴△ABF≌△CDH(ASA),
同理:△BCG≌△DAE(ASA),
∵AM⊥BC,∠ABC=60°,
∴∠BAM=30°,
∴BM=AB=2,
∴AM=BM=2,BC=2BM,
∵∠BGC=90°,
∴BM=CM=GM=2,
∴∠CMG=2∠CBG=30°,
∵GN⊥BC,
∴GN=GM=1,
∴S菱形ABCD=BC AM=4×2=8,
S△ABF=AF BF=×2×2=4,
S△BCG=BC GN=×4×1=2,
∴S矩形EFGH=S菱形ABCD-2S△ABF-2S△BCG=8-12.
故答案为:8-12.
18.
解:如图,连接AC,取AC的中点O,连接BO,OQ,
∵矩形ABCD中,AB=3,AD=BC=,
∴,
∵点O是AC的中点,∠ABC=90°,
∴AO=BO=CO=3,
∴AB=AO=BO=3,
∴△ABO是等边三角形,
∴∠BAO=60°,
∵△APQ是等边三角形,
∴AP=AQ,∠PAQ=∠BAO=60°,
∴∠BAP=∠QAC,
在△ABP和△AOQ中,
∴△ABP≌△AOQ(SAS),
∴∠ABP=∠AOQ=90°,
∴OQ是AC的垂直平分线,
∴AQ=CQ,
∵CQ+DQ=AQ+QD,
∴当点A,点Q,点D三点共线时,CQ+DQ的最小值为AD长,
∴CQ+DQ的最小值为,
故答案为:.
19.
解:过点A作AC⊥y轴于点C,
∵,
∴.
∵四边形为矩形
∴AM=BM=DM=,
∴,,
∴
∴△ABM是等边三角形.
又∵AC⊥y轴,
∴CM,
∴,
∴点A坐标为.
故答案为:.
20.16
解:如图,连接,
则阴影部分的面积,
图中长方形的面积是,
故答案为:.
21.
解:由翻折可得CD=OD,∠CDF=∠BDF,
∵四边形ABCD为矩形,
∴OC=OD,AB=CD,AD=BC=3,∠BCD=∠ABC=90°,
∴OC=OD=CD,
即△OCD为等边三角形,
∴∠BDC=60°,
∴CDBC,∠CDF=∠BDF=30°,
∴CFCD=1,
∴BF=BC﹣CF=2,
在Rt△ABF中,由勾股定理可得,
AF.
故答案为:.
22.3
解:如图,连接,
四边形是矩形,且,
,
,
垂直平分,
,
设,则,
在中,,即,
解得,
即.
23.(1)见解析 (2)
(1)
证明:∵四边形ABCD是矩形,
∴AD=BC,ADBC,
∵AE=CF,
∴DE=BF,DEBF,
∴四边形BFDE是平行四边形;
(2)
解:∵四边形BFDE是平行四边形,EF⊥BD,
∴四边形BFDE是菱形,
∴DE=BE,
∵四边形ABCD是矩形,
∴∠A=90°,
在Rt△ABE中,BE=DE=AD-AE=4-AE,AB=2,
根据勾股定理得:BE2=AE2+AB2,
∴(4-AE)2=AE2+22,
解得AE=.
24.(1)见解析 (2)5
(1)
证明:∵四边形ABCD是矩形,
∴ABCD,
∴∠M=∠N,
∵AC的垂直平分线是MN,
∴AO=CO,
在△AOM和△CON中,
,
∴△AOM≌△CON(AAS);
(2)
解:连接CE,设AE=x,则DE=8﹣x,
∵AC的垂直平分线是MN,
∴AE=CE=x,
∵四边形ABCD是矩形,AB=4,
∴DC=AB=4,∠ADC=90°,
由勾股定理得:,
∴,
解得:x=5,
即AE=5.
25.(1) (2)见解析
(1)
解:如图1所示,
∵四边形ABCD是矩形,
∴∠C=90°,CD=AB=3,AD=BC=4,
∴DE=AD=4,
在Rt△CDE中,CE,
∴BE=BC﹣CE=4;
(2)
如图2,连接BM,
∵点M是DE的中点,
∴DM=EM,
∵BD=BE,
∴△BDE是等腰三角形,
∴BM⊥DE,
∴∠BMD=90°,
∵四边形ABCD是矩形,
∴∠BCD=∠ADC=90°,AD=BC,
∴∠DCE=180°-∠BCD=90°,
∴△CDE是直角三角形,
∵M为DE的中点,
∴DM=CM,
∴∠CDM=∠DCM,
∴∠BCD+∠DCM=∠CDM+∠ADC,
∴∠ADM=∠BCM,
在△ADM和△BCM中,
,
∴△ADM≌△BCM(SAS).
∴∠AMD=∠BMC,
∴∠AMC=∠AMB+∠BMC=∠AMB+∠AMD=∠BMD=90°,
∴AM⊥CM;
26.(1)见解析
(2)见解析
(3)8+8
(1)
证明:∵四边形ABCD为矩形,
∴ADBC,∠DAB=∠ABE=90°,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴∠BAE=∠AEB=45°,
∴AB=EB,
∵四边形ABCD为矩形,
∴∠ABC=∠BCD=90°,AB=CD,
∵BF=CF,
∴∠FBC=∠FCB,
∴∠ABF=∠DCF,
在△ABF和△AFD中,
∴△ABF≌△AFD(SAS),
∴AF=DF,
∴∠ADF=∠DAE=45°,
∴∠AFD=90°,
∴∠ABE=∠AFD=90°,
∵AE=AD,
在△ABE和△AFD中,
∴△ABE≌△AFD(AAS),
∴AB=AF;
(2)
证明:∵AE=AD,∠EAD=45°,
∴∠AED=∠ADE=67.5°,
∴∠FDG=22.5°,
∵AB=AF,∠BAF=45°,
∴∠AFB=67.5°,
∴∠EFG=67.5°,
∴∠EFG=∠AED,
∴FG=EG,
∵∠AFD=90°,
∴∠DFE=90°,
∵∠EFG=67.5°,
∴∠DFG=∠DFE-∠EFG =22.5°,
∴∠DFG=∠FDG,
∴FG=DG,
∴EG=DG;
(3)
解:∵EG=2,
∴ED=4,
设AB=BE=x,
则AD=AE=x,DF=AF=AB=x,
∴EF=x﹣x,
∴,
∴x2=8+4,
∴.
27.(1)证明见解析
(2)
(3)∠CAG=60°
(1)
证明:四边形是平行四边形,
,,
,,
平分,
,
,
,
又四边形是平行四边形,
是菱形;
(2)
解:,
四边形是矩形,
,
,
,
菱形是正方形,
,,,
,
,
,
,
,
,
,,
,
,
;
(3)
解:如图3,延长,,交于点,连接,
四边形是平行四边形,,
,,,
四边形是菱形,
,,,
,,
四边形是平行四边形,四边形是平行四边形,,
,
,
,
四边形是菱形,
,,
是等边三角形,是等边三角形,
,,
,
,
.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
