11.2.1 第3课时 直角三角形的性质和判定 课件(共18张PPT)
文档属性
| 名称 | 11.2.1 第3课时 直角三角形的性质和判定 课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 07:49:35 | ||
图片预览


文档简介
(共18张PPT)
11.2 与三角形有关的角
11.2.1 三角形的内角
精品同步教学课件
第3课时 直角三角形的性质和判定
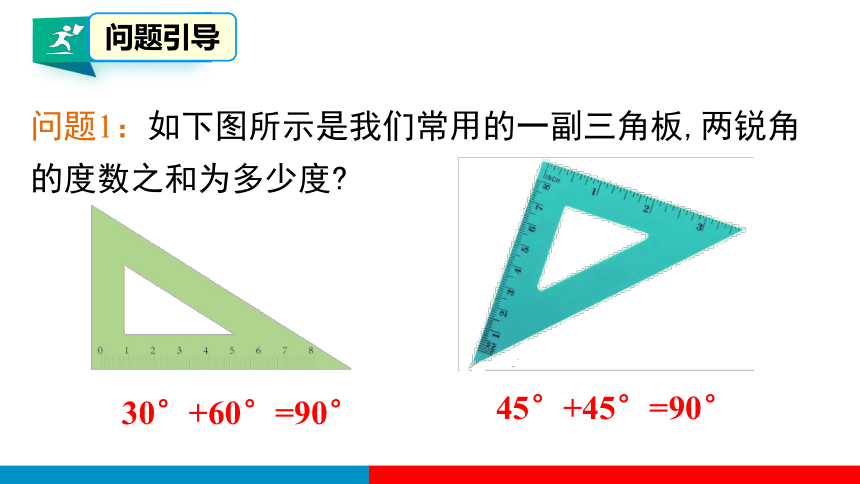
问题1:如下图所示是我们常用的一副三角板,两锐角的度数之和为多少度
30°+60°=90°
45°+45°=90°
讲授新课
问题引导
问题2:如图,在直角△ABC中, ∠C=90°,两锐角的和等于多少呢?
在直角△ABC中,因为 ∠C=90°,由三角形内角和定理,得∠A +∠B+∠C=180°,即
∠A +∠B=90°.
思考:由此,你可以得到直角三角形有什么性质呢?
A
B
C
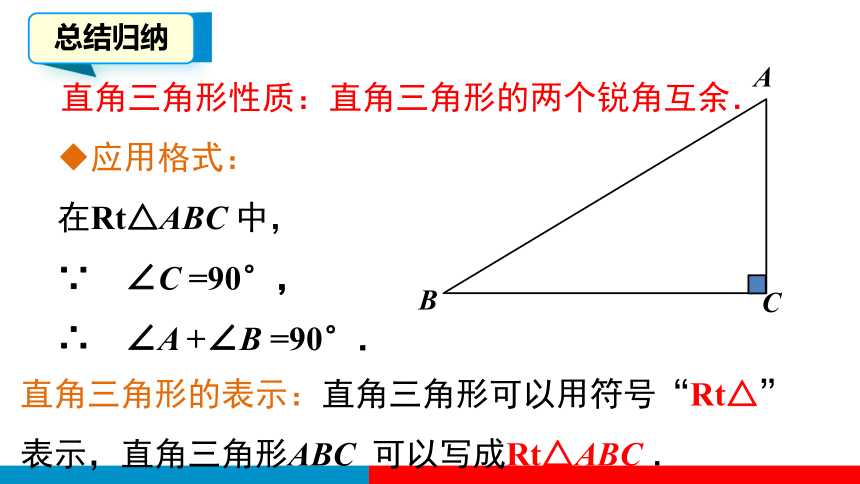
直角三角形性质:直角三角形的两个锐角互余.
应用格式:
在Rt△ABC 中,
∵ ∠C =90°,
∴ ∠A +∠B =90°.
直角三角形的表示:直角三角形可以用符号“Rt△”表示,直角三角形ABC 可以写成Rt△ABC .
总结归纳
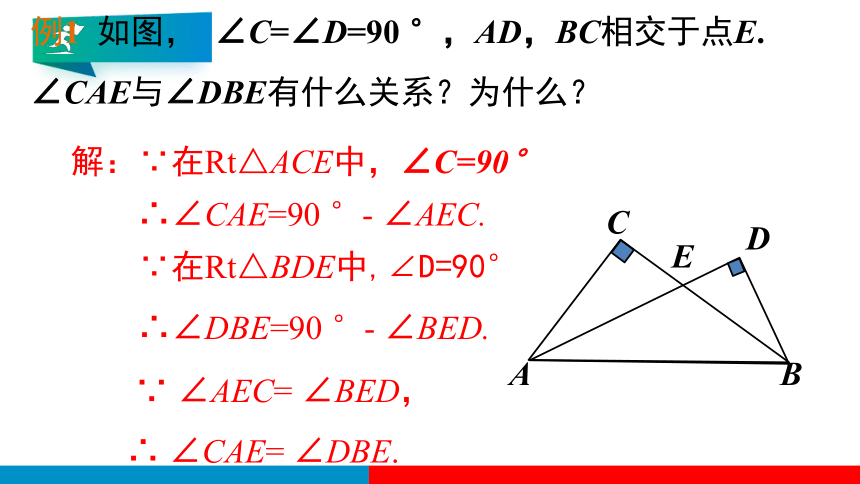
例1 如图, ∠C=∠D=90 °,AD,BC相交于点E. ∠CAE与∠DBE有什么关系?为什么?
A
B
C
D
E
解:∵在Rt△ACE中,∠C=90°
∴∠CAE=90 °- ∠AEC.
∵在Rt△BDE中,∠D=90°
∴∠DBE=90 °- ∠BED.
∵ ∠AEC= ∠BED,
∴ ∠CAE= ∠DBE.
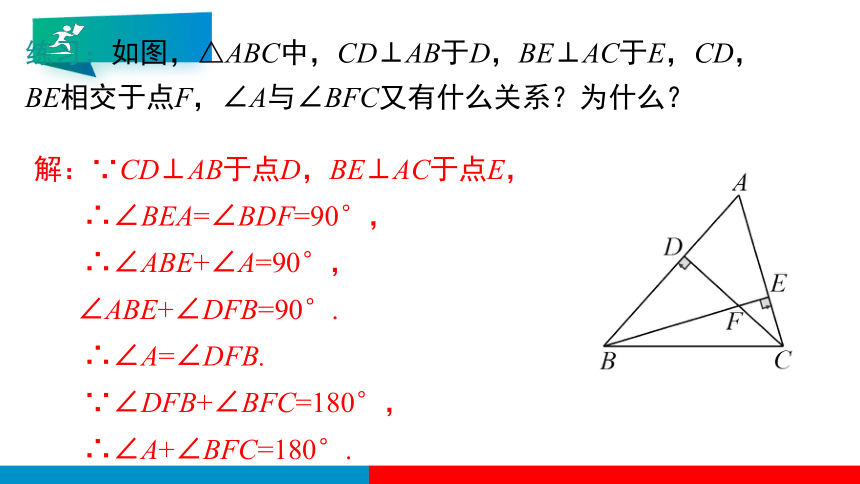
解:∵CD⊥AB于点D,BE⊥AC于点E,
∴∠BEA=∠BDF=90°,
∴∠ABE+∠A=90°,
∠ABE+∠DFB=90°.
∴∠A=∠DFB.
∵∠DFB+∠BFC=180°,
∴∠A+∠BFC=180°.
练习:如图,△ABC中,CD⊥AB于D,BE⊥AC于E,CD,BE相交于点F,∠A与∠BFC又有什么关系?为什么?
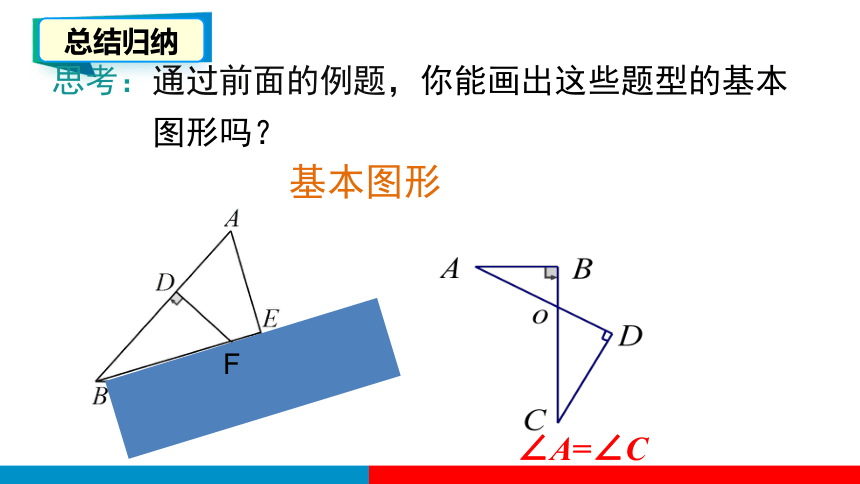
思考:通过前面的例题,你能画出这些题型的基本
图形吗?
基本图形
∠A=∠C
总结归纳
F
问题:有两个角互余的三角形是直角三角形吗?
如图,在△ABC中, ∠A +∠B=90° , 那么△ABC
是直角三角形吗?
在△ABC中,因为 ∠A +∠B +∠C=180°, 又∠A +∠B=90°,所以∠C=90°. 于是△ABC是直角三角形.
直角三角形判定
二
A
B
C
应用格式:
在△ABC 中,
∵ ∠A +∠B =90°,
∴ △ABC 是直角三角形.
有两个角互余的三角形是直角三角形.
总结归纳
典例精析
例2 如图,∠C=90 °, ∠1= ∠2,△ADE是直角三角形吗?为什么?
A
C
B
D
E
(
(
1
2
解:在Rt△ABC中,
∠2+ ∠A=90 °.
∵ ∠1= ∠2,
∴∠1 + ∠A=90 °.
即△ADE是直角三角形.
思考:你能得到这个题的基本模型和结论吗?
练习:如图,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.求证:△ACD是直角三角形.
证明:∵∠ACB=90°,
∴∠A+∠B=90°.
∵∠ACD=∠B,
∴∠A+∠ACD=90°,
∴△ACD是直角三角形.
思考:你能得到这个题的基本模型和结论吗?
如图11.2-5,AB ∥ CD,直线EF 分别交AB,CD 于点E,F,∠ BEF 的平分线与∠ DFE 的平分线相交于点P.
求证:△ EFP 是直角三角形.
练习
解题秘方:如果三角形中有两个角的和等于90°(互余)就可证明该三角形为直角三角形.
证明:∵ AB ∥ CD,
∴∠ BEF+ ∠ DFE=180°.
又∵ EP 平分∠ BEF,FP 平分∠ DFE,
∴∠ PEF= ∠ BEF,∠ PFE= ∠ DFE.
∴∠PEF+ ∠PFE= (∠BEF+ ∠DFE)=
×180°=90°.
∴△ EFP 是直角三角形.
练习:如图11.2-6,在△ ABC 中,∠ ACB=90°,∠ ACD=
∠ B. 求证:CD ⊥ AB.
解题秘方:利用直角三角形的性质与判定求出CD,AB 的夹角为直角.
证明:∵∠ ACB=90°,
∴∠ A+ ∠ B=90°(直角三角形的性质).
∵∠ ACD= ∠ B,∴∠ A+ ∠ ACD=90°(等量代换).
∴∠ CDA=90°(直角三角形的判定). ∴ CD ⊥ AB.
课堂小结
直角三角形的性质与判定
性质
直角三角形的两个锐角互余
判定
有两个角互余的三角形是直角三角形
https://www.21cnjy.com/help/help_extract.php
11.2 与三角形有关的角
11.2.1 三角形的内角
精品同步教学课件
第3课时 直角三角形的性质和判定
问题1:如下图所示是我们常用的一副三角板,两锐角的度数之和为多少度
30°+60°=90°
45°+45°=90°
讲授新课
问题引导
问题2:如图,在直角△ABC中, ∠C=90°,两锐角的和等于多少呢?
在直角△ABC中,因为 ∠C=90°,由三角形内角和定理,得∠A +∠B+∠C=180°,即
∠A +∠B=90°.
思考:由此,你可以得到直角三角形有什么性质呢?
A
B
C
直角三角形性质:直角三角形的两个锐角互余.
应用格式:
在Rt△ABC 中,
∵ ∠C =90°,
∴ ∠A +∠B =90°.
直角三角形的表示:直角三角形可以用符号“Rt△”表示,直角三角形ABC 可以写成Rt△ABC .
总结归纳
例1 如图, ∠C=∠D=90 °,AD,BC相交于点E. ∠CAE与∠DBE有什么关系?为什么?
A
B
C
D
E
解:∵在Rt△ACE中,∠C=90°
∴∠CAE=90 °- ∠AEC.
∵在Rt△BDE中,∠D=90°
∴∠DBE=90 °- ∠BED.
∵ ∠AEC= ∠BED,
∴ ∠CAE= ∠DBE.
解:∵CD⊥AB于点D,BE⊥AC于点E,
∴∠BEA=∠BDF=90°,
∴∠ABE+∠A=90°,
∠ABE+∠DFB=90°.
∴∠A=∠DFB.
∵∠DFB+∠BFC=180°,
∴∠A+∠BFC=180°.
练习:如图,△ABC中,CD⊥AB于D,BE⊥AC于E,CD,BE相交于点F,∠A与∠BFC又有什么关系?为什么?
思考:通过前面的例题,你能画出这些题型的基本
图形吗?
基本图形
∠A=∠C
总结归纳
F
问题:有两个角互余的三角形是直角三角形吗?
如图,在△ABC中, ∠A +∠B=90° , 那么△ABC
是直角三角形吗?
在△ABC中,因为 ∠A +∠B +∠C=180°, 又∠A +∠B=90°,所以∠C=90°. 于是△ABC是直角三角形.
直角三角形判定
二
A
B
C
应用格式:
在△ABC 中,
∵ ∠A +∠B =90°,
∴ △ABC 是直角三角形.
有两个角互余的三角形是直角三角形.
总结归纳
典例精析
例2 如图,∠C=90 °, ∠1= ∠2,△ADE是直角三角形吗?为什么?
A
C
B
D
E
(
(
1
2
解:在Rt△ABC中,
∠2+ ∠A=90 °.
∵ ∠1= ∠2,
∴∠1 + ∠A=90 °.
即△ADE是直角三角形.
思考:你能得到这个题的基本模型和结论吗?
练习:如图,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.求证:△ACD是直角三角形.
证明:∵∠ACB=90°,
∴∠A+∠B=90°.
∵∠ACD=∠B,
∴∠A+∠ACD=90°,
∴△ACD是直角三角形.
思考:你能得到这个题的基本模型和结论吗?
如图11.2-5,AB ∥ CD,直线EF 分别交AB,CD 于点E,F,∠ BEF 的平分线与∠ DFE 的平分线相交于点P.
求证:△ EFP 是直角三角形.
练习
解题秘方:如果三角形中有两个角的和等于90°(互余)就可证明该三角形为直角三角形.
证明:∵ AB ∥ CD,
∴∠ BEF+ ∠ DFE=180°.
又∵ EP 平分∠ BEF,FP 平分∠ DFE,
∴∠ PEF= ∠ BEF,∠ PFE= ∠ DFE.
∴∠PEF+ ∠PFE= (∠BEF+ ∠DFE)=
×180°=90°.
∴△ EFP 是直角三角形.
练习:如图11.2-6,在△ ABC 中,∠ ACB=90°,∠ ACD=
∠ B. 求证:CD ⊥ AB.
解题秘方:利用直角三角形的性质与判定求出CD,AB 的夹角为直角.
证明:∵∠ ACB=90°,
∴∠ A+ ∠ B=90°(直角三角形的性质).
∵∠ ACD= ∠ B,∴∠ A+ ∠ ACD=90°(等量代换).
∴∠ CDA=90°(直角三角形的判定). ∴ CD ⊥ AB.
课堂小结
直角三角形的性质与判定
性质
直角三角形的两个锐角互余
判定
有两个角互余的三角形是直角三角形
https://www.21cnjy.com/help/help_extract.php
