2022-2023学年冀教版八年级数学上册13.3三角形全等的判定 解答专项练习题 (含解析)
文档属性
| 名称 | 2022-2023学年冀教版八年级数学上册13.3三角形全等的判定 解答专项练习题 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 254.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-24 09:16:46 | ||
图片预览



文档简介
2022-2023学年冀教版八年级数学上册《13.3三角形全等的判定》解答专项练习题(附答案)
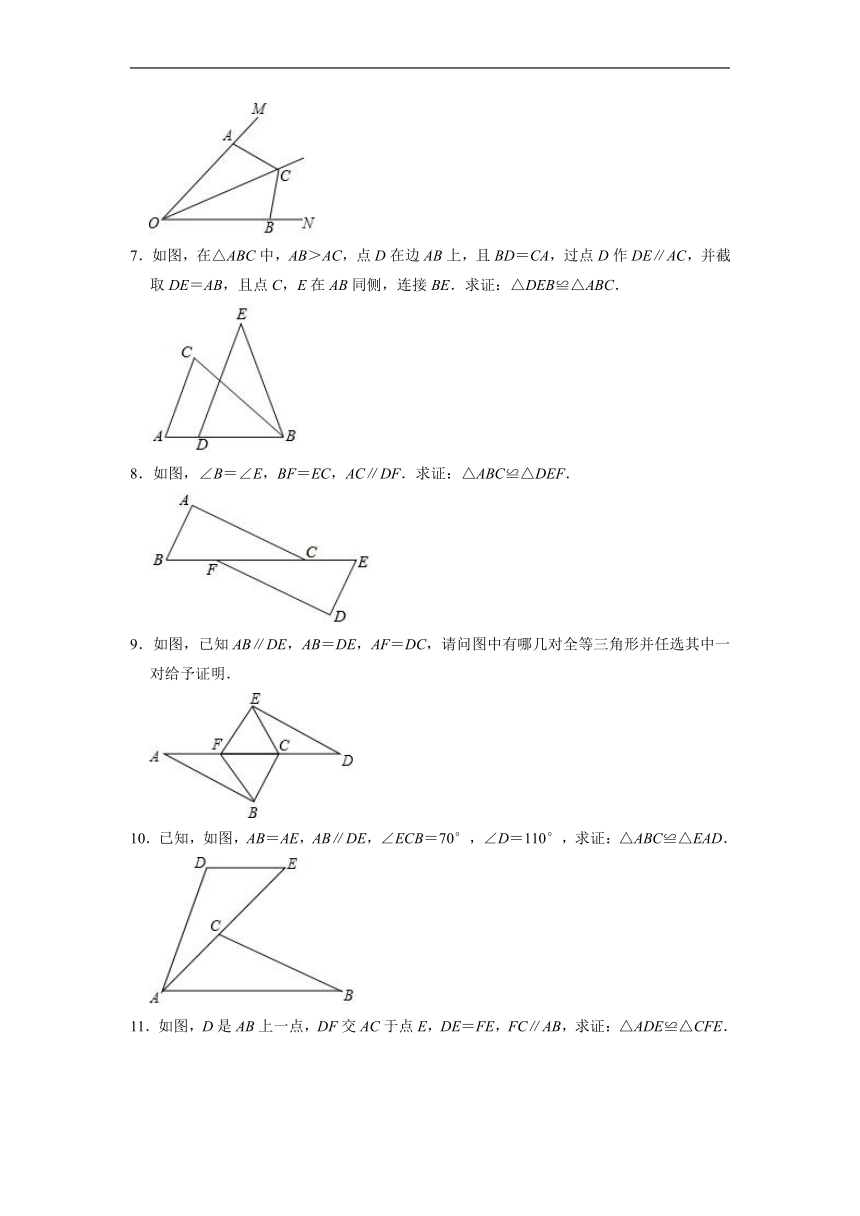
1.如图,B是线段AC的中点,AD∥BE,BD∥CE.求证:△ABD≌△BCE.
2.如图,点A、B、D、E在同一条直线上,AB=DE,AC∥DF,BC∥EF.求证:△ABC≌△DEF.
3.如图,在Rt△ABC中,∠B=90°,CD∥AB,DE⊥AC于点E,且CE=AB.求证:△CED≌△ABC.
4.如图,点C在BD上,AB⊥BD,ED⊥BD,AC⊥CE,AB=CD.求证:△ABC≌△CDE.
5.如图,已知OA=OC,OB=OD,∠AOC=∠BOD.
求证:△AOB≌△COD.
6.如图,已知OC平分∠MON,点A、B分别在射线OM,ON上,且OA=OB.
求证:△AOC≌△BOC.
7.如图,在△ABC中,AB>AC,点D在边AB上,且BD=CA,过点D作DE∥AC,并截取DE=AB,且点C,E在AB同侧,连接BE.求证:△DEB≌△ABC.
8.如图,∠B=∠E,BF=EC,AC∥DF.求证:△ABC≌△DEF.
9.如图,已知AB∥DE,AB=DE,AF=DC,请问图中有哪几对全等三角形并任选其中一对给予证明.
10.已知,如图,AB=AE,AB∥DE,∠ECB=70°,∠D=110°,求证:△ABC≌△EAD.
11.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,求证:△ADE≌△CFE.
12.已知命题:如图,点A,D,B,E在同一条直线上,且AD=BE,∠A=∠FDE,则△ABC≌△DEF.判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,请添加一个适当条件使它成为真命题,并加以证明.
13.如图,AE和BD相交于点C,∠A=∠E,AC=EC.求证:△ABC≌△EDC.
14.如图,已知AC平分∠BAD,AB=AD.求证:△ABC≌△ADC.
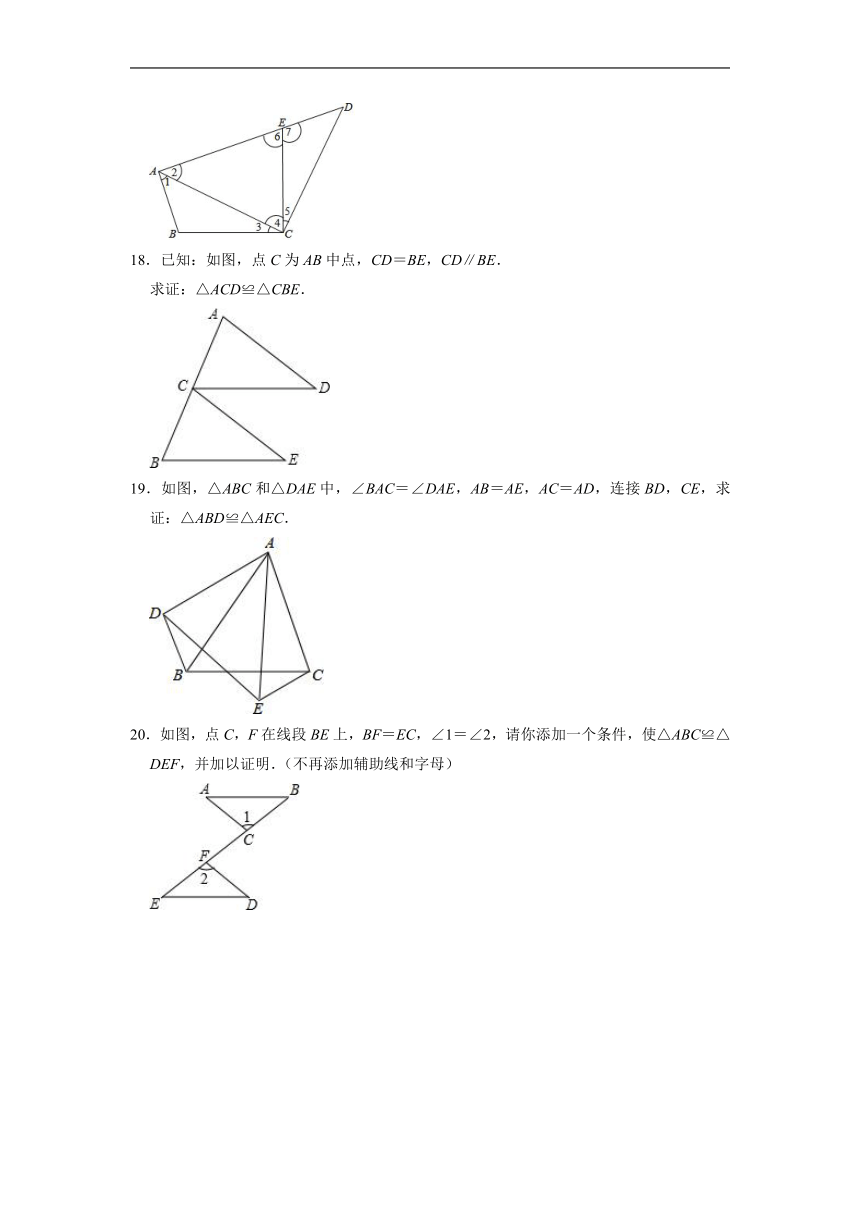
15.如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.求证:△ADF≌△BCE.
16.如图,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC,并说明理由.
17.如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC与△DEC全等.
18.已知:如图,点C为AB中点,CD=BE,CD∥BE.
求证:△ACD≌△CBE.
19.如图,△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE,求证:△ABD≌△AEC.
20.如图,点C,F在线段BE上,BF=EC,∠1=∠2,请你添加一个条件,使△ABC≌△DEF,并加以证明.(不再添加辅助线和字母)
参考答案
1.证明:∵点B为线段AC的中点,
∴AB=BC,
∵AD∥BE,
∴∠A=∠EBC,
∵BD∥CE,
∴∠C=∠DBA,
在△ABD与△BCE中,
,
∴△ABD≌△BCE.(ASA).
2.证明:∵AC∥DF,
∴∠CAB=∠FDE(两直线平行,同位角相等),
又∵BC∥EF,
∴∠CBA=∠FED(两直线平行,同位角相等),
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA).
3.证明:∵DE⊥AC,∠B=90°,
∴∠DEC=∠B=90°,
∵CD∥AB,
∴∠A=∠DCE,
在△CED和△ABC中,
,
∴△CED≌△ABC(ASA).
4.证明:∵AB⊥BD,ED⊥BD,AC⊥CE,
∴∠B=∠D=∠ACE=90°,
∴∠DCE+∠DEC=90°,∠BCA+∠DCE=90°,
∴∠BCA=∠DEC,
在△ABC和△CDE中,
,
∴△ABC≌△CDE(AAS).
5.证明:∵∠AOC=∠BOD,
∴∠AOC﹣∠AOD=∠BOD﹣∠AOD,
即∠COD=∠AOB,
在△AOB和△COD中,
,
∴△AOB≌△COD(SAS).
6.证明:∵OC平分∠MON,
∴∠AOC=∠BOC,
在△AOC和△BOC中,
,
∴△AOC≌△BOC(SAS).
7.证明:∵DE∥AC,
∴∠EDB=∠A.
在△DEB与△ABC中,
,
∴△DEB≌△ABC(SAS).
8.证明:∵AC∥DF,
∴∠ACB=∠DFE,
∵BF=CE,
∴BC=EF,
在△ABC和△DEF中,,
∴△ABC≌△DEF(ASA).
9.解:此图中有三对全等三角形.分别是:△ABF≌△DEC、△ABC≌△DEF、△BCF≌△EFC.
证明:∵AB∥DE,
∴∠A=∠D.
又∵AB=DE、AF=DC,
∴△ABF≌△DEC.
10.证明:由∠ECB=70°得∠ACB=110°
又∵∠D=110°
∴∠ACB=∠D
∵AB∥DE
∴∠CAB=∠E
在△ABC和△EAD中,
,
∴△ABC≌△EAD(AAS).
11.证明:∵FC∥AB,
∴∠A=∠FCE,∠ADE=∠F,
在△ADE与△CFE中:
∵,
∴△ADE≌△CFE(AAS).
12.解:是假命题.
以下任一方法均可:
①添加条件:AC=DF.
证明:∵AD=BE,
∴AD+BD=BE+BD,即AB=DE.
在△ABC和△DEF中,
AB=DE,
∠A=∠FDE,
AC=DF,
∴△ABC≌△DEF(SAS);
②添加条件:∠CBA=∠E.
证明:∵AD=BE,
∴AD+BD=BE+BD,即AB=DE.
在△ABC和△DEF中,
∠A=∠FDE,
AB=DE,
∠CBA=∠E,
∴△ABC≌△DEF(ASA);
③添加条件:∠C=∠F.
证明:∵AD=BE,
∴AD+BD=BE+BD,即AB=DE.
在△ABC和△DEF中,
∠A=∠FDE,
∠C=∠F,
AB=DE,
∴△ABC≌△DEF(AAS).
13.证明:∵在△ABC和△EDC中,
,
∴△ABC≌△EDC(ASA).
14.证明:∵AC平分∠BAD,
∴∠BAC=∠DAC,
在△ABC和△ADC中,
,
∴△ABC≌△ADC(SAS).
15.解:∵AE=BF,
∴AE+EF=BF+EF,
∴AF=BE,
在△ADF与△BCE中,
∴△ADF≌△BCE(SAS)
16.解:添加∠BAC=∠DAC.理由如下:
在△ABC与△ADC中,
,
∴△ABC≌△ADC(AAS).
17.解:∵∠BCE=∠ACD=90°,
∴∠3+∠4=∠4+∠5,
∴∠3=∠5,
在△ACD中,∠ACD=90°,
∴∠2+∠D=90°,
∵∠BAE=∠1+∠2=90°,
∴∠1=∠D,
在△ABC和△DEC中,
,
∴△ABC≌△DEC(AAS).
18.证明:∵C是AB的中点(已知),
∴AC=CB(线段中点的定义).
∵CD∥BE(已知),
∴∠ACD=∠B(两直线平行,同位角相等).
在△ACD和△CBE中,
,
∴△ACD≌△CBE(SAS).
19.证明:∵∠BAC=∠DAE,
∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,
即∠BAD=∠CAE,
在△ABD和△AEC中,
,
∴△ABD≌△AEC(SAS).
20.AC=DF.
证明:∵BF=EC,
∴BF﹣CF=EC﹣CF,
∴BC=EF,
在△ABC和△DEF中
∴△ABC≌△DEF(SAS).
1.如图,B是线段AC的中点,AD∥BE,BD∥CE.求证:△ABD≌△BCE.
2.如图,点A、B、D、E在同一条直线上,AB=DE,AC∥DF,BC∥EF.求证:△ABC≌△DEF.
3.如图,在Rt△ABC中,∠B=90°,CD∥AB,DE⊥AC于点E,且CE=AB.求证:△CED≌△ABC.
4.如图,点C在BD上,AB⊥BD,ED⊥BD,AC⊥CE,AB=CD.求证:△ABC≌△CDE.
5.如图,已知OA=OC,OB=OD,∠AOC=∠BOD.
求证:△AOB≌△COD.
6.如图,已知OC平分∠MON,点A、B分别在射线OM,ON上,且OA=OB.
求证:△AOC≌△BOC.
7.如图,在△ABC中,AB>AC,点D在边AB上,且BD=CA,过点D作DE∥AC,并截取DE=AB,且点C,E在AB同侧,连接BE.求证:△DEB≌△ABC.
8.如图,∠B=∠E,BF=EC,AC∥DF.求证:△ABC≌△DEF.
9.如图,已知AB∥DE,AB=DE,AF=DC,请问图中有哪几对全等三角形并任选其中一对给予证明.
10.已知,如图,AB=AE,AB∥DE,∠ECB=70°,∠D=110°,求证:△ABC≌△EAD.
11.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,求证:△ADE≌△CFE.
12.已知命题:如图,点A,D,B,E在同一条直线上,且AD=BE,∠A=∠FDE,则△ABC≌△DEF.判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,请添加一个适当条件使它成为真命题,并加以证明.
13.如图,AE和BD相交于点C,∠A=∠E,AC=EC.求证:△ABC≌△EDC.
14.如图,已知AC平分∠BAD,AB=AD.求证:△ABC≌△ADC.
15.如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.求证:△ADF≌△BCE.
16.如图,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC,并说明理由.
17.如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC与△DEC全等.
18.已知:如图,点C为AB中点,CD=BE,CD∥BE.
求证:△ACD≌△CBE.
19.如图,△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE,求证:△ABD≌△AEC.
20.如图,点C,F在线段BE上,BF=EC,∠1=∠2,请你添加一个条件,使△ABC≌△DEF,并加以证明.(不再添加辅助线和字母)
参考答案
1.证明:∵点B为线段AC的中点,
∴AB=BC,
∵AD∥BE,
∴∠A=∠EBC,
∵BD∥CE,
∴∠C=∠DBA,
在△ABD与△BCE中,
,
∴△ABD≌△BCE.(ASA).
2.证明:∵AC∥DF,
∴∠CAB=∠FDE(两直线平行,同位角相等),
又∵BC∥EF,
∴∠CBA=∠FED(两直线平行,同位角相等),
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA).
3.证明:∵DE⊥AC,∠B=90°,
∴∠DEC=∠B=90°,
∵CD∥AB,
∴∠A=∠DCE,
在△CED和△ABC中,
,
∴△CED≌△ABC(ASA).
4.证明:∵AB⊥BD,ED⊥BD,AC⊥CE,
∴∠B=∠D=∠ACE=90°,
∴∠DCE+∠DEC=90°,∠BCA+∠DCE=90°,
∴∠BCA=∠DEC,
在△ABC和△CDE中,
,
∴△ABC≌△CDE(AAS).
5.证明:∵∠AOC=∠BOD,
∴∠AOC﹣∠AOD=∠BOD﹣∠AOD,
即∠COD=∠AOB,
在△AOB和△COD中,
,
∴△AOB≌△COD(SAS).
6.证明:∵OC平分∠MON,
∴∠AOC=∠BOC,
在△AOC和△BOC中,
,
∴△AOC≌△BOC(SAS).
7.证明:∵DE∥AC,
∴∠EDB=∠A.
在△DEB与△ABC中,
,
∴△DEB≌△ABC(SAS).
8.证明:∵AC∥DF,
∴∠ACB=∠DFE,
∵BF=CE,
∴BC=EF,
在△ABC和△DEF中,,
∴△ABC≌△DEF(ASA).
9.解:此图中有三对全等三角形.分别是:△ABF≌△DEC、△ABC≌△DEF、△BCF≌△EFC.
证明:∵AB∥DE,
∴∠A=∠D.
又∵AB=DE、AF=DC,
∴△ABF≌△DEC.
10.证明:由∠ECB=70°得∠ACB=110°
又∵∠D=110°
∴∠ACB=∠D
∵AB∥DE
∴∠CAB=∠E
在△ABC和△EAD中,
,
∴△ABC≌△EAD(AAS).
11.证明:∵FC∥AB,
∴∠A=∠FCE,∠ADE=∠F,
在△ADE与△CFE中:
∵,
∴△ADE≌△CFE(AAS).
12.解:是假命题.
以下任一方法均可:
①添加条件:AC=DF.
证明:∵AD=BE,
∴AD+BD=BE+BD,即AB=DE.
在△ABC和△DEF中,
AB=DE,
∠A=∠FDE,
AC=DF,
∴△ABC≌△DEF(SAS);
②添加条件:∠CBA=∠E.
证明:∵AD=BE,
∴AD+BD=BE+BD,即AB=DE.
在△ABC和△DEF中,
∠A=∠FDE,
AB=DE,
∠CBA=∠E,
∴△ABC≌△DEF(ASA);
③添加条件:∠C=∠F.
证明:∵AD=BE,
∴AD+BD=BE+BD,即AB=DE.
在△ABC和△DEF中,
∠A=∠FDE,
∠C=∠F,
AB=DE,
∴△ABC≌△DEF(AAS).
13.证明:∵在△ABC和△EDC中,
,
∴△ABC≌△EDC(ASA).
14.证明:∵AC平分∠BAD,
∴∠BAC=∠DAC,
在△ABC和△ADC中,
,
∴△ABC≌△ADC(SAS).
15.解:∵AE=BF,
∴AE+EF=BF+EF,
∴AF=BE,
在△ADF与△BCE中,
∴△ADF≌△BCE(SAS)
16.解:添加∠BAC=∠DAC.理由如下:
在△ABC与△ADC中,
,
∴△ABC≌△ADC(AAS).
17.解:∵∠BCE=∠ACD=90°,
∴∠3+∠4=∠4+∠5,
∴∠3=∠5,
在△ACD中,∠ACD=90°,
∴∠2+∠D=90°,
∵∠BAE=∠1+∠2=90°,
∴∠1=∠D,
在△ABC和△DEC中,
,
∴△ABC≌△DEC(AAS).
18.证明:∵C是AB的中点(已知),
∴AC=CB(线段中点的定义).
∵CD∥BE(已知),
∴∠ACD=∠B(两直线平行,同位角相等).
在△ACD和△CBE中,
,
∴△ACD≌△CBE(SAS).
19.证明:∵∠BAC=∠DAE,
∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,
即∠BAD=∠CAE,
在△ABD和△AEC中,
,
∴△ABD≌△AEC(SAS).
20.AC=DF.
证明:∵BF=EC,
∴BF﹣CF=EC﹣CF,
∴BC=EF,
在△ABC和△DEF中
∴△ABC≌△DEF(SAS).
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
