视图（2）[上学期]

第二课时 视图(二)
教学目标
知识与技能
能由实物抽象出几何体,会画直棱柱的三种视图．
过程与方法
通过画三棱柱和四棱柱的三种视图，体会这两种几何体与其视图之间的关系,培养学生空间想象能力,发展学生空间观念.
情感态度与价值观
通过学习和实践活动，激发学生对视图学习的好奇心，体会数学与现实生活的密切联系，了解数学的价值，增进对数学的理解和学好数学的信心;通过具体的学习活动，积累数学活动经验，养成积极主动参与数学活动的习惯。
教学重难点
画直三棱柱和直四棱柱的三种视图.
教学过程
创设问题情境，引入新课
在上节课，我们学习了画圆柱、圆锥，球的三种视图，并能根据视图找出对应的物体，体会了这几种几何体与其视图之间的相互转化，那么，对于直棱柱应如何画出它的三种视图呢 本节课我们将一起进行有关方面的学习．
新知探究
1、画直三棱柱与直四棱柱的三种视图投影片：
(1)你能想象出图1中各几何体的主视图、左视图和俯视图吗 你能画出它们吗
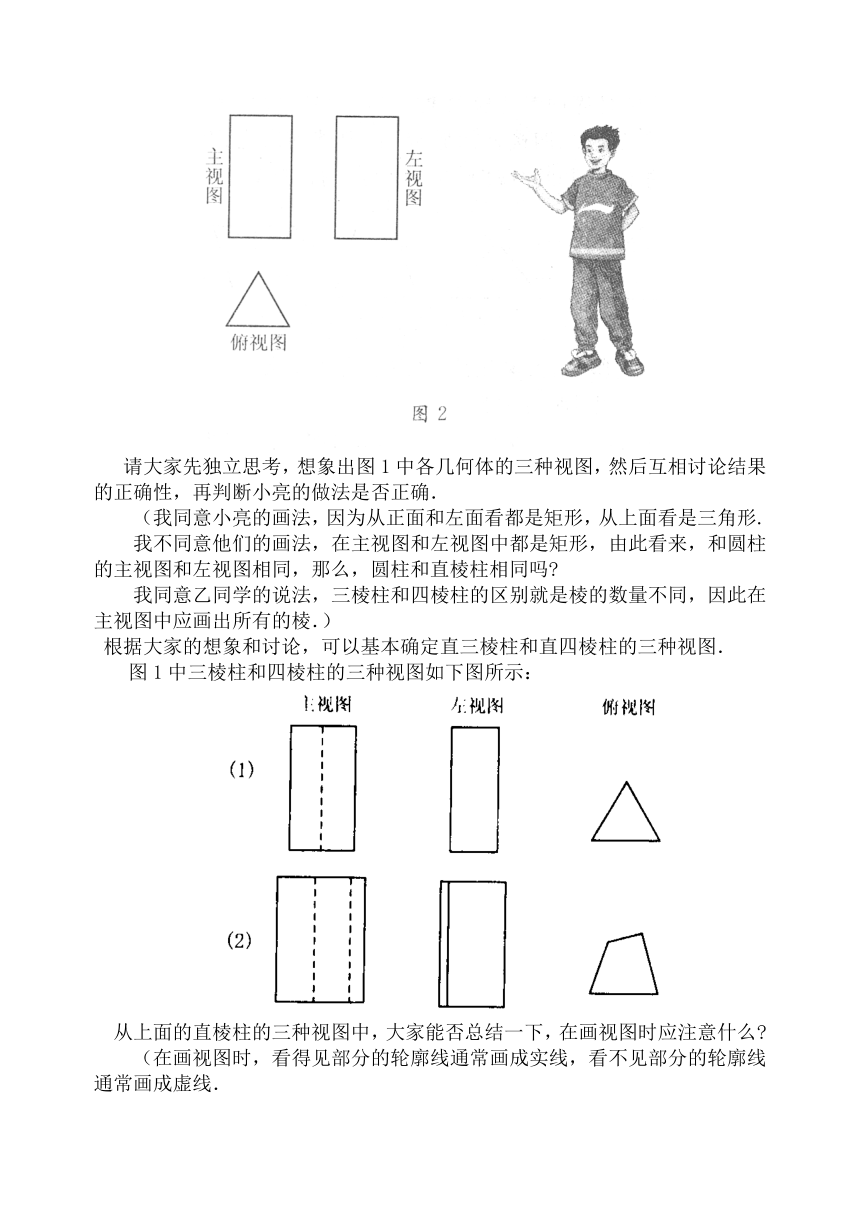
(2)小亮画出了其中一个几何体的主视图、左视图和俯视图(如图2)，你同意他的画法吗 你能画出另一个几何体的三种视图吗
请大家先独立思考，想象出图1中各几何体的三种视图，然后互相讨论结果的正确性，再判断小亮的做法是否正确．
（我同意小亮的画法，因为从正面和左面看都是矩形，从上面看是三角形.
我不同意他们的画法，在主视图和左视图中都是矩形，由此看来，和圆柱的主视图和左视图相同，那么，圆柱和直棱柱相同吗
我同意乙同学的说法，三棱柱和四棱柱的区别就是棱的数量不同，因此在主视图中应画出所有的棱．）
根据大家的想象和讨论，可以基本确定直三棱柱和直四棱柱的三种视图．
图1中三棱柱和四棱柱的三种视图如下图所示：
从上面的直棱柱的三种视图中，大家能否总结一下，在画视图时应注意什么
（在画视图时，看得见部分的轮廓线通常画成实线，看不见部分的轮廓线通常画成虚线．
主视图和左视图是否同样宽应注意．）
2、做一做
下图是底面为等腰直角三角形和等腰梯形的三棱柱、四棱柱的俯视图，尝试画出它们的主视图和左视图．并与同伴进行交流．
请大家先独立完成，再互相交流．
视图如下：
下面请大家思考几个问题：
(1)在两个三棱柱的视图中，应把棱柱的所有棱都画出来，看得见的画实线，看不见的画线，为什么这儿只画两条棱呢 是不是画错了
(2)在两个底面是等腰梯形的四棱柱中，为什么一个主视图中画两条虚线，一个主视图中都是实线呢
(3)上面这种画法足否唯—呢
（(1)应该是画三条棱，只是在这种放置方法中，有两条棱在视线方向上互相重合了，因此只出现了一条棱，并没有画错．
(2)还是因为放置方法的不同，在(3)中有两条棱看得见，两条棱看不见，因此四条棱中有两条虚线，两条实线；在(4)中四条棱都能看得见，因此都为实线．
(3)上面这种画法不是唯一的，因为棱柱的高度不明确．）
课堂练习
已知某四棱柱的俯视图如下图所示，尝试画出它的主视图和左视图．
视图如下：
归纳提炼
本节课我们学习了如何根据实物画直三棱柱和直四棱柱的三种视图，以及根据三种视图中的，一种画出另外两种视图，充分体现直三棱柱和直四棱柱与其视图之间的相互转化过程，还讨论了在画视图过程中应注意的事项．
课后作业
习题4．2
活动与探究
下列几何体的三种视图有没有错误(不考虑尺寸) 为什么？如果错了，应该怎样改正
答案：1．
2、用小立方块搭一个几何体，使它的主视图和俯视图如图所示。这样的几何体只有一种吗？它最少需要多少个小立方块？最多需要多少个小立方块？
备课资料
华罗庚
华罗庚．世界著名的数学家，江苏金坛人，然而你相信吗 这个闻名于世的大数学家，却仅有初中毕业文凭，他19岁时写出的数学论文《苏家驹之代数的五次方程式解法不能成立之理由》轰动了整个数学界，1938年，他在昆明西南联大任教授，1946年应邀到美国讲学，被聘为终身教授，1950年华罗庚放弃了在美同优越的生活条件．毅然回国．他主要的著作有《推垒素数沦》《数论导引》《统筹学评估》《优选法评估》等．
1985年6月12日下午，年过七旬，满头银发的华罗庚精神矍铄地出现在东京大学的讲台上，他兴致勃勃地演讲．这次演讲持续了1小时零5分钟，他的心脏病突然发作……他实现了生前多次表示过的愿望——工作到生命的最后一刻!一代数学伟人在远离祖国的他乡倒了下去，他永远地离开了我们．离开了他为之奋斗一生的数学研究事业.