4.3.3余角和补角 课件(共28张PPT)
文档属性
| 名称 | 4.3.3余角和补角 课件(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-24 19:57:59 | ||
图片预览





文档简介
(共28张PPT)
人教版七年级上册
4.3.3余角和补角
教学目标
教学目标: 1、理解余角、补角的意义及其性质。
2、初步掌握图形语言与符号语言之间的相互转化。
3、运用余角、补角的性质解决一些简单的问题。
教学重点: 理解余角、补角的意义及其性质。
教学难点:运用余角、补角的性质解决一些简单的问题。
新知导入
情境引入
比萨斜塔建于1173年,工程曾间断了两次,历经约二百年才完工,设计为垂直建造,但是在工程开始后不久便由于地基不均匀和土层松软而倾斜,你知道比萨斜塔倾斜多少度角吗?它现在与地面成多少度角?
倾斜了约3.97°.
它现在与地面成的夹角约是86.03°.
这两个角之和是多少
新知讲解
合作学习
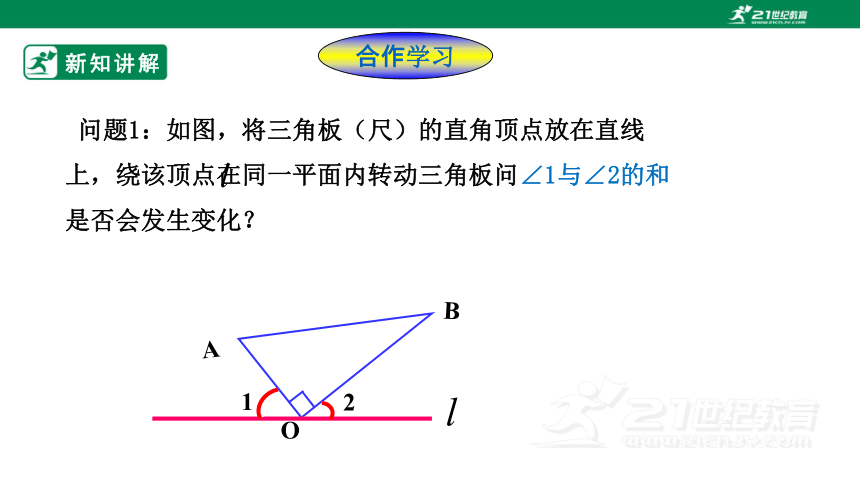
问题1:如图,将三角板(尺)的直角顶点放在直线 上,绕该顶点在同一平面内转动三角板问∠1与∠2的和是否会发生变化?
O
A
B
1
2
l
如果两个角的和等于90 (直角),就说这两个角互为余角,
即其中每一个角是另一个角的余角.
1
2
∵ ∠1+∠2=90°
∴∠1与∠2互为余角
∵∠1与∠2互为余角
∴ ∠1+∠2=90°
试一试:判断
①32°与58°互为余角。
②∠1+∠2 +∠3= 90°,
则∠1、∠2 、∠3 互为余角。
③两个锐角一定互为余角。
( √ )
( × )
( × )
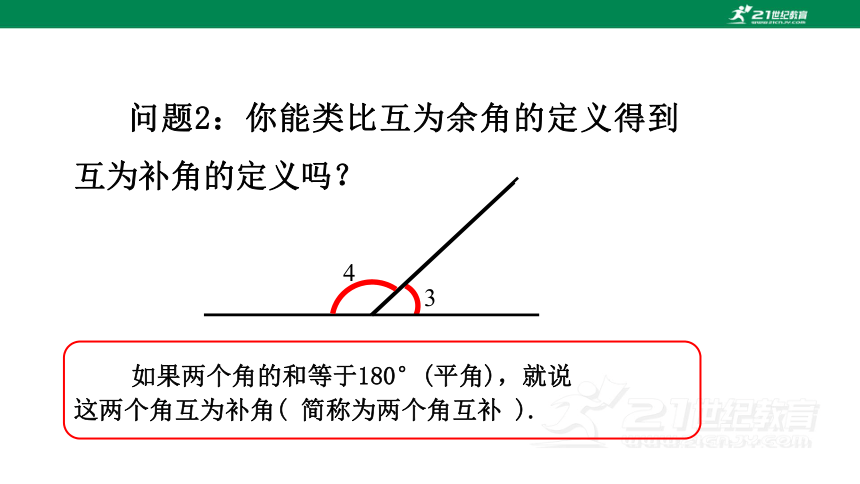
如果两个角的和等于180°(平角),就说
这两个角互为补角( 简称为两个角互补 ).
4
3
问题2:你能类比互为余角的定义得到互为补角的定义吗?
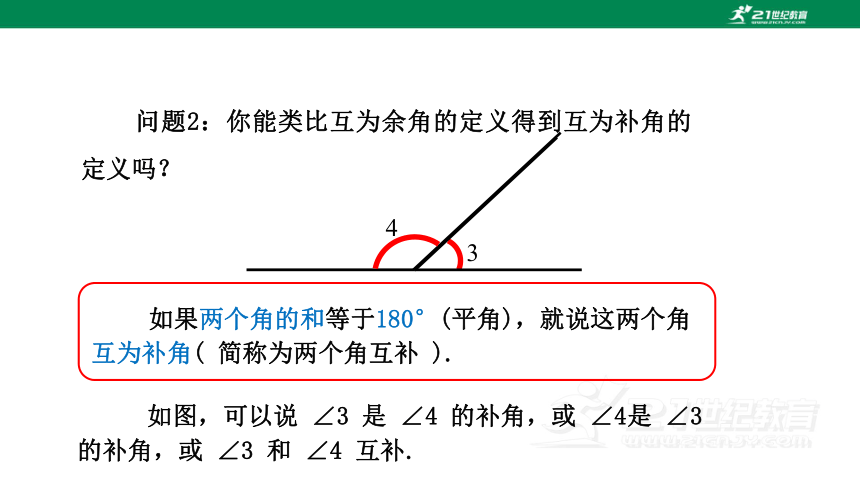
如图,可以说 ∠3 是 ∠4 的补角,或 ∠4是 ∠3 的补角,或 ∠3 和 ∠4 互补.
4
3
问题2:你能类比互为余角的定义得到互为补角的定义吗?
如果两个角的和等于180°(平角),就说这两个角互为补角( 简称为两个角互补 ).
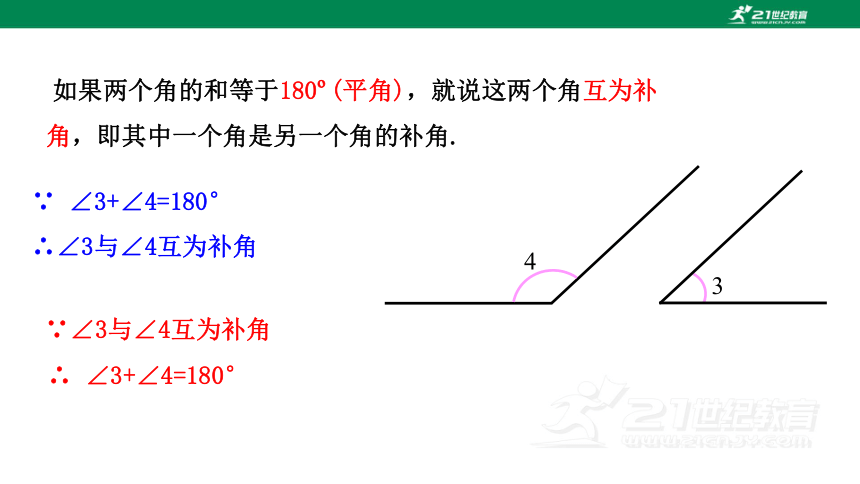
如果两个角的和等于180 (平角),就说这两个角互为补角,即其中一个角是另一个角的补角.
4
3
∵ ∠3+∠4=180°
∴∠3与∠4互为补角
∵∠3与∠4互为补角
∴ ∠3+∠4=180°
问题3:∠1和∠2互余,∠1也与∠3互余,请问∠2与∠3是什么关系?
1
2
所以∠2=∠3
3
1
解:因为∠1+∠2=90°,∠1+∠3=90°
所以∠2=90°-∠1,∠3=90°-∠1
问题4:若∠1与∠2互余,∠3与∠4互余,
如果∠1=∠3,那么∠2和∠4相等吗?
解:∠2与∠4相等
因为∠1=∠3,
所以∠2=∠4
1
2
4
3
所以90°-∠1=90°-∠3
性质:同角 (等角) 的余角相等.
问题5:对于补角是否也有类似性质?
1
1
问题5:对于补角是否也有类似性质?
1
2
4
3
性质:同角 (等角) 的补角相等.
典例精讲
例1 如图,点A,O, B在同一条直线 上,射线OD和射线
OE分别平分∠AOC和∠BOC, 图中哪些角互为余角?
解:因为点A,O, B在同一条直线上,
所以 ∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC和∠BOC,
所以∠COD+∠COE= ∠AOC+ ∠BOC
= (∠AOC+∠BOC)= 90°.
所以,∠COD和∠COE互为余角,
同理,∠AOD和∠BOE,∠AOD和∠COE,
∠COD和∠BOE也互为余角.
O
A
B
C
D
E
1.定义:以正北、正南方向为基准,描述物体运动的方向,即正北、正南方向与物体运动方向的夹角为方位角.
注意事项:方位角在叙述时,一般先说南北,后说东西,
如南偏东30°.但与南北方向夹角为45°时,常简称为东北、东南、西北、西南,如南偏东45°,即为东南方向.
知识:方位角
甲地
乙地
北
观测点
被观测点
如何表示在甲地观察乙地的方位角?
1.先找到观测点,然后画出方向指标;
甲地
乙地
北
视线
2.把观测点和被观测点用线段连接起来;
如何表示在甲地观察乙地的方位角?
3.度量正北或正南方向的射线和视线之间的角度,就是所求方位角了。
例4 如图,货轮O在航行过程中,发现灯塔A在它南偏东60 的方向上.同时,在它北偏东40 、南偏西10 、西北(即北偏西45 )方向上又分别发现了客轮B、货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D方向的射线.
画法:以点O为顶点,表示正北方向的射线为角的一边,画40°的角,使它的另一边OB落在东和北之间.射线OB的方向就是北偏东40°,即客轮B所在的方向.同理,可以画出表示货轮C和海岛D方向的射线.
东
南
西
北
60°
● B
40°
10°
45°
C ●
● D
O
●
● A
归纳概念
3种思想方法:特殊——一般,类比、化归
2条基本性质:余角的性质、补角的性质
2种数学核心素养:直观想象,逻辑推理
课堂练习
1.如图所示,∠AOB=∠COD=90°,那么∠AOC=∠BOD,这是根据( ) A.直角都相等 B.同角的余角相等
C.同角的补角相等 D.互为余角的两个角相等
2.如图所示,点O在直线AE上,OB平分∠AOC,∠BOD=90°,则∠DOE和∠COB的关系是( )
A.互余 B.互补 C.相等 D.和是钝角
B
A
3. 如图,下面说法中不正确的是( )
A.射线OA表示北偏东30°
B.射线OB表示西北方向
C.射线OC表示西偏南80°
D.射线OD表示南偏东70°
C
4. 一个角的补角比它的余角的3倍小20°,求这个角的度数.
解:设这个角的度数为x°.
由题意,得180-x=3(90-x)-20,
解得x=35.
答:这个角的度数为35°.
5. 如图,D是直线EF上一点,∠CDE=90°,∠1=∠2,哪些角互为余角?哪些角互为补角?
解:∠1与∠ADC,∠1与∠BDC,∠2与∠BDC,∠2与∠ADC互为余角;
∠1与∠ADF,∠2与∠ADF,∠2与∠BDE,∠1与∠BDE,∠EDC与∠FDC互为补角.
课堂总结
余角和补角
余角
补角
两个角的和等于90
两个角的和等于180
定义
性质
同(等)角的余角相等
定义
性质
同(等)角的补角相等
方位角
正北、正南方向与物体运动方向的夹角为方位角
表示方向的角在航 行、测绘等工作中经常 用到
定义
应用
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版七年级上册
4.3.3余角和补角
教学目标
教学目标: 1、理解余角、补角的意义及其性质。
2、初步掌握图形语言与符号语言之间的相互转化。
3、运用余角、补角的性质解决一些简单的问题。
教学重点: 理解余角、补角的意义及其性质。
教学难点:运用余角、补角的性质解决一些简单的问题。
新知导入
情境引入
比萨斜塔建于1173年,工程曾间断了两次,历经约二百年才完工,设计为垂直建造,但是在工程开始后不久便由于地基不均匀和土层松软而倾斜,你知道比萨斜塔倾斜多少度角吗?它现在与地面成多少度角?
倾斜了约3.97°.
它现在与地面成的夹角约是86.03°.
这两个角之和是多少
新知讲解
合作学习
问题1:如图,将三角板(尺)的直角顶点放在直线 上,绕该顶点在同一平面内转动三角板问∠1与∠2的和是否会发生变化?
O
A
B
1
2
l
如果两个角的和等于90 (直角),就说这两个角互为余角,
即其中每一个角是另一个角的余角.
1
2
∵ ∠1+∠2=90°
∴∠1与∠2互为余角
∵∠1与∠2互为余角
∴ ∠1+∠2=90°
试一试:判断
①32°与58°互为余角。
②∠1+∠2 +∠3= 90°,
则∠1、∠2 、∠3 互为余角。
③两个锐角一定互为余角。
( √ )
( × )
( × )
如果两个角的和等于180°(平角),就说
这两个角互为补角( 简称为两个角互补 ).
4
3
问题2:你能类比互为余角的定义得到互为补角的定义吗?
如图,可以说 ∠3 是 ∠4 的补角,或 ∠4是 ∠3 的补角,或 ∠3 和 ∠4 互补.
4
3
问题2:你能类比互为余角的定义得到互为补角的定义吗?
如果两个角的和等于180°(平角),就说这两个角互为补角( 简称为两个角互补 ).
如果两个角的和等于180 (平角),就说这两个角互为补角,即其中一个角是另一个角的补角.
4
3
∵ ∠3+∠4=180°
∴∠3与∠4互为补角
∵∠3与∠4互为补角
∴ ∠3+∠4=180°
问题3:∠1和∠2互余,∠1也与∠3互余,请问∠2与∠3是什么关系?
1
2
所以∠2=∠3
3
1
解:因为∠1+∠2=90°,∠1+∠3=90°
所以∠2=90°-∠1,∠3=90°-∠1
问题4:若∠1与∠2互余,∠3与∠4互余,
如果∠1=∠3,那么∠2和∠4相等吗?
解:∠2与∠4相等
因为∠1=∠3,
所以∠2=∠4
1
2
4
3
所以90°-∠1=90°-∠3
性质:同角 (等角) 的余角相等.
问题5:对于补角是否也有类似性质?
1
1
问题5:对于补角是否也有类似性质?
1
2
4
3
性质:同角 (等角) 的补角相等.
典例精讲
例1 如图,点A,O, B在同一条直线 上,射线OD和射线
OE分别平分∠AOC和∠BOC, 图中哪些角互为余角?
解:因为点A,O, B在同一条直线上,
所以 ∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC和∠BOC,
所以∠COD+∠COE= ∠AOC+ ∠BOC
= (∠AOC+∠BOC)= 90°.
所以,∠COD和∠COE互为余角,
同理,∠AOD和∠BOE,∠AOD和∠COE,
∠COD和∠BOE也互为余角.
O
A
B
C
D
E
1.定义:以正北、正南方向为基准,描述物体运动的方向,即正北、正南方向与物体运动方向的夹角为方位角.
注意事项:方位角在叙述时,一般先说南北,后说东西,
如南偏东30°.但与南北方向夹角为45°时,常简称为东北、东南、西北、西南,如南偏东45°,即为东南方向.
知识:方位角
甲地
乙地
北
观测点
被观测点
如何表示在甲地观察乙地的方位角?
1.先找到观测点,然后画出方向指标;
甲地
乙地
北
视线
2.把观测点和被观测点用线段连接起来;
如何表示在甲地观察乙地的方位角?
3.度量正北或正南方向的射线和视线之间的角度,就是所求方位角了。
例4 如图,货轮O在航行过程中,发现灯塔A在它南偏东60 的方向上.同时,在它北偏东40 、南偏西10 、西北(即北偏西45 )方向上又分别发现了客轮B、货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D方向的射线.
画法:以点O为顶点,表示正北方向的射线为角的一边,画40°的角,使它的另一边OB落在东和北之间.射线OB的方向就是北偏东40°,即客轮B所在的方向.同理,可以画出表示货轮C和海岛D方向的射线.
东
南
西
北
60°
● B
40°
10°
45°
C ●
● D
O
●
● A
归纳概念
3种思想方法:特殊——一般,类比、化归
2条基本性质:余角的性质、补角的性质
2种数学核心素养:直观想象,逻辑推理
课堂练习
1.如图所示,∠AOB=∠COD=90°,那么∠AOC=∠BOD,这是根据( ) A.直角都相等 B.同角的余角相等
C.同角的补角相等 D.互为余角的两个角相等
2.如图所示,点O在直线AE上,OB平分∠AOC,∠BOD=90°,则∠DOE和∠COB的关系是( )
A.互余 B.互补 C.相等 D.和是钝角
B
A
3. 如图,下面说法中不正确的是( )
A.射线OA表示北偏东30°
B.射线OB表示西北方向
C.射线OC表示西偏南80°
D.射线OD表示南偏东70°
C
4. 一个角的补角比它的余角的3倍小20°,求这个角的度数.
解:设这个角的度数为x°.
由题意,得180-x=3(90-x)-20,
解得x=35.
答:这个角的度数为35°.
5. 如图,D是直线EF上一点,∠CDE=90°,∠1=∠2,哪些角互为余角?哪些角互为补角?
解:∠1与∠ADC,∠1与∠BDC,∠2与∠BDC,∠2与∠ADC互为余角;
∠1与∠ADF,∠2与∠ADF,∠2与∠BDE,∠1与∠BDE,∠EDC与∠FDC互为补角.
课堂总结
余角和补角
余角
补角
两个角的和等于90
两个角的和等于180
定义
性质
同(等)角的余角相等
定义
性质
同(等)角的补角相等
方位角
正北、正南方向与物体运动方向的夹角为方位角
表示方向的角在航 行、测绘等工作中经常 用到
定义
应用
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
