2.1 等式性质与不等式性质 课件(共28张PPT)
文档属性
| 名称 | 2.1 等式性质与不等式性质 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-24 12:10:01 | ||
图片预览








文档简介
数学
第二章 一元二次函数、方程和不等式
2.1 等式性质与不等式性质
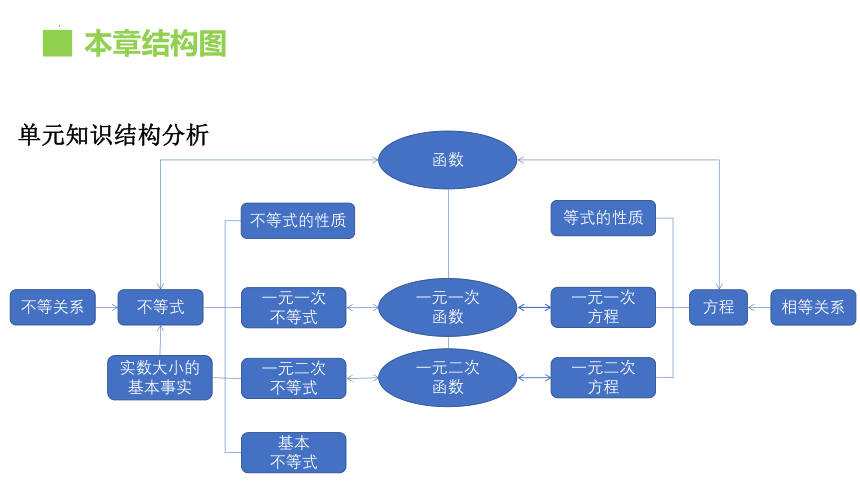
本章结构图
单元知识结构分析
函数
一元一次
函数
一元二次
函数
等式的性质
一元一次
方程
一元二次
方程
方程
相等关系
不等式
实数大小的基本事实
不等式的性质
一元一次
不等式
一元二次
不等式
基本
不等式
不等关系
人与人的年龄大小、高矮胖瘦,物与物的形状结构,事与事的成因与结果的不同等等都表现出不等关系,这表明现实世界中的量,不等是普遍的、绝对的,而相等则是局部的、相对的。
不等关系
问题引入
0 <v ≤40.
?
如图,设C是直线AB外的任意一点,CD⊥AB于点D,E是直线AB上不同于D的任意一点,连接线段CE,则CD<CE.
????≥2.5%????≥2.3%
?
设△ABC的三条边为a,b,c,则 a + b > c ,a – b < c .
问题引入
常用文字语言与数学符号语言
文字语言
大于,高于,超过
小于,低于,少于
大于等于,
至少,不低于
小于等于,
至多,不多于,不超过
符号语言
>
<
我们用数学符号“≠”,“>”,“<”,“≥”,“≤”连接两个数或代数式,以表示它们之间的不等关系.含有这些不等号的式子叫做不等式.
问题引入
解:设提价后每本杂志的定价为 x 元.
销售量: (8???????2.50.1×0.2)万本.
?
不等关系:销售总收入不低于20万.
问题2. 某种杂志原以每本2.5元的价格销售,可以售出8万本.据市场调査,杂志的单价每提高0.1元,销售量就可能减少2000本,如何定价才能使提价后的销售总收入不低于20万元?
销售总收入: (8???????2.50.1×0.2)x万元.
?
(8???????2.50.1×0.2)x 20.
?
求出不等式的解集,就能知道满足条件的杂志的定价范围。
那么,求不等式的解集就需要借助不等式的性质.
新知讲授
两个实数a,b,其大小关系有三种可能,即a>b,a=b,a知识点一 基本事实
依据
a>b? .
a=b? .
a结论
要比较两个实数的大小,可以转化为比较它们的 与 __的大小(作差法)
a-b>0
a-b=0
a-b<0
差
0
例题巩固
作差法
例题巩固
解 ∵a3+b3-(a2b+ab2)
=(a3-a2b)+(b3-ab2)
=a2(a-b)+b2(b-a)
=(a-b)(a2-b2)=(a-b)2(a+b).
当a=b时,a-b=0,a3+b3=a2b+ab2;
当a≠b时,(a-b)2>0,a+b>0,a3+b3>a2b+ab2.
综上所述,当a=b时,a3+b3=a2b+ab2;
当a≠b时,a3+b3>a2b+ab2.
例2 已知a,b均为正实数.试利用作差法比较a3+b3与a2b+ab2的大小.
①作差
②变形
?
③判断差的符号
?
??④下结论
?
方法归纳
反思感悟 作差法比较两个实数大小的基本步骤(后续证明函数的单调性)
新知探究
4×12????????
?
正方形
ABCD的面积
4个直角三角形的面积和
????2+????2
?
D
A
B
C
G
H
F
E
????2+????2
?
a
b
????≠????
?
>
追问1:如果直角三角形的两条直角边边长分别为????,b (a≠b),你能将发现的不等关系用不等式表示吗?
?
大于
追问2:如果直角三角形的两条直角边边长相等(????=????),不等式 ????2+????2>2????????还成立吗?
?
D
A
B
C
G
H
F
E
????2+????2
?
=
?
2????????
?
要点 重要不等式
?????,????∈????, 有 ????2+????2≥2????????,?当且仅当????=????时,等号成立.
?
追问3:?????,????∈R,????2+????2≥2????????,这个猜想成立吗?请证明.
?
????2+????2?2?????????
?
=?(?????????)2 ≥0
?
当且仅当????=????时,等号成立.
?
新知讲授
课堂练习
课堂练习
1. 已知????>????
实际问题、几何图形
不等关系
两个实数大小关系的基本事实(作差法)
不等式
不等式
性质
数学抽象
?
等式性质与不等式性质(1)
课堂小结
复习回顾
1.如果a=b,那么 .
2.如果a=b,b=c,那么 .
3.如果a=b,那么a±c=b±c.
4.如果a=b,那么ac=bc.
5.如果a=b,c≠0,那么=
b=a
a=c
对称性
传递性
四则运算中的不变性
新知探究
性质
别名
性质内容
注意
1
相反性
a>b?b a
?
2
传递性
a>b,b>c?a>c
不可逆
3
可加性
a>b?a+c b+c
可逆
4
可乘性
a>b,c>0?_____ __
a>b,c<0?_____ _
c的符号
5
同向可加性
a>b,c>d? ___________
同向
6
同向同正可乘性
a>b>0,c>d>0?________
同向
7
同正可乘方性
a>b>0?an bn(n∈N,n≥2)
同正
新知探究
性质
性质内容
8
a>b ? -a -b
9
a>b>0 0 1???? ?1????
0>a>b 1???? ?1???? 0
a>0>b 1???? 0 ?1????
性质
性质内容
8
a>b ? -a -b
9
1.若a>b,则a-c>b-c.( )
2. >1?a>b.( )
3.a>b?ac2>bc2.( )
4.a>b?a+c>b+c.( )
5. ?a+c>b+d.( )
思考辨析 判断正误
×
√
×
×
√
作商法
例题巩固
一、利用不等式的性质判断命题的真假
课本42页
方法总结
利用不等式性质判断命题真假的注意点
(1)运用不等式的性质判断时,要注意不等式成立的条件,不要弱化条件,尤其是不能凭想当然随意捏造性质.
(2)采用特殊值法进行排除,取值一定要遵循如下原则:
一是满足题设条件;二是取值要简单,便于验证计算.
例题巩固
一、利用不等式的性质判断命题的真假
课本57页
例题巩固
例. 已知2≤a≤3,-2≤b≤-1,则2a+b的取值范围是_____________.
二、利用不等式的性质求范围
∵4≤2a≤6,-2≤b≤-1
∴2≤2a+b≤5.
例. 已知2≤a≤3,-2≤b≤-1,则2a-b的取值范围是_____________.
∵-2≤b≤-1,∴ 1≤-b≤2.
4≤2a≤6,∴5≤2a-b≤8.
例题巩固
二、利用不等式的性质求范围
(延伸)已知0解析 因为0方法归纳
反思感悟
利用不等式的性质求取值范围的策略
(1)建立待求范围的整体与已知范围的整体的关系,最后利用一次不等式的性质进行运算,求得待求的范围.
(2)同向(异向)不等式的两边可以相加(相减),这种转化不是等价变形,如果在解题过程中多次使用这种转化,就有可能扩大其取值范围.
注意:求解这种不等式问题要特别注意不能简单地分别求出单个变量的范围,再去求其他不等式的范围.
课堂练习
已知-1≤x+y≤4,2≤x-y≤3,则z=2x-3y的取值范围是_____________.
课堂小结
实际问题、
几何问题
不等关系
两个实数大小关系的基本事实(作差法)
不等式
不等式
性质
数学抽象
性质的应用
判断命题的真假
等式性质与不等式性质(2)
基本不等式
第二章 一元二次函数、方程和不等式
2.1 等式性质与不等式性质
本章结构图
单元知识结构分析
函数
一元一次
函数
一元二次
函数
等式的性质
一元一次
方程
一元二次
方程
方程
相等关系
不等式
实数大小的基本事实
不等式的性质
一元一次
不等式
一元二次
不等式
基本
不等式
不等关系
人与人的年龄大小、高矮胖瘦,物与物的形状结构,事与事的成因与结果的不同等等都表现出不等关系,这表明现实世界中的量,不等是普遍的、绝对的,而相等则是局部的、相对的。
不等关系
问题引入
0 <v ≤40.
?
如图,设C是直线AB外的任意一点,CD⊥AB于点D,E是直线AB上不同于D的任意一点,连接线段CE,则CD<CE.
????≥2.5%????≥2.3%
?
设△ABC的三条边为a,b,c,则 a + b > c ,a – b < c .
问题引入
常用文字语言与数学符号语言
文字语言
大于,高于,超过
小于,低于,少于
大于等于,
至少,不低于
小于等于,
至多,不多于,不超过
符号语言
>
<
我们用数学符号“≠”,“>”,“<”,“≥”,“≤”连接两个数或代数式,以表示它们之间的不等关系.含有这些不等号的式子叫做不等式.
问题引入
解:设提价后每本杂志的定价为 x 元.
销售量: (8???????2.50.1×0.2)万本.
?
不等关系:销售总收入不低于20万.
问题2. 某种杂志原以每本2.5元的价格销售,可以售出8万本.据市场调査,杂志的单价每提高0.1元,销售量就可能减少2000本,如何定价才能使提价后的销售总收入不低于20万元?
销售总收入: (8???????2.50.1×0.2)x万元.
?
(8???????2.50.1×0.2)x 20.
?
求出不等式的解集,就能知道满足条件的杂志的定价范围。
那么,求不等式的解集就需要借助不等式的性质.
新知讲授
两个实数a,b,其大小关系有三种可能,即a>b,a=b,a
依据
a>b? .
a=b? .
a
要比较两个实数的大小,可以转化为比较它们的 与 __的大小(作差法)
a-b>0
a-b=0
a-b<0
差
0
例题巩固
作差法
例题巩固
解 ∵a3+b3-(a2b+ab2)
=(a3-a2b)+(b3-ab2)
=a2(a-b)+b2(b-a)
=(a-b)(a2-b2)=(a-b)2(a+b).
当a=b时,a-b=0,a3+b3=a2b+ab2;
当a≠b时,(a-b)2>0,a+b>0,a3+b3>a2b+ab2.
综上所述,当a=b时,a3+b3=a2b+ab2;
当a≠b时,a3+b3>a2b+ab2.
例2 已知a,b均为正实数.试利用作差法比较a3+b3与a2b+ab2的大小.
①作差
②变形
?
③判断差的符号
?
??④下结论
?
方法归纳
反思感悟 作差法比较两个实数大小的基本步骤(后续证明函数的单调性)
新知探究
4×12????????
?
正方形
ABCD的面积
4个直角三角形的面积和
????2+????2
?
D
A
B
C
G
H
F
E
????2+????2
?
a
b
????≠????
?
>
追问1:如果直角三角形的两条直角边边长分别为????,b (a≠b),你能将发现的不等关系用不等式表示吗?
?
大于
追问2:如果直角三角形的两条直角边边长相等(????=????),不等式 ????2+????2>2????????还成立吗?
?
D
A
B
C
G
H
F
E
????2+????2
?
=
?
2????????
?
要点 重要不等式
?????,????∈????, 有 ????2+????2≥2????????,?当且仅当????=????时,等号成立.
?
追问3:?????,????∈R,????2+????2≥2????????,这个猜想成立吗?请证明.
?
????2+????2?2?????????
?
=?(?????????)2 ≥0
?
当且仅当????=????时,等号成立.
?
新知讲授
课堂练习
课堂练习
1. 已知????>????
实际问题、几何图形
不等关系
两个实数大小关系的基本事实(作差法)
不等式
不等式
性质
数学抽象
?
等式性质与不等式性质(1)
课堂小结
复习回顾
1.如果a=b,那么 .
2.如果a=b,b=c,那么 .
3.如果a=b,那么a±c=b±c.
4.如果a=b,那么ac=bc.
5.如果a=b,c≠0,那么=
b=a
a=c
对称性
传递性
四则运算中的不变性
新知探究
性质
别名
性质内容
注意
1
相反性
a>b?b a
?
2
传递性
a>b,b>c?a>c
不可逆
3
可加性
a>b?a+c b+c
可逆
4
可乘性
a>b,c>0?_____ __
a>b,c<0?_____ _
c的符号
5
同向可加性
a>b,c>d? ___________
同向
6
同向同正可乘性
a>b>0,c>d>0?________
同向
7
同正可乘方性
a>b>0?an bn(n∈N,n≥2)
同正
新知探究
性质
性质内容
8
a>b ? -a -b
9
a>b>0 0 1???? ?1????
0>a>b 1???? ?1???? 0
a>0>b 1???? 0 ?1????
性质
性质内容
8
a>b ? -a -b
9
1.若a>b,则a-c>b-c.( )
2. >1?a>b.( )
3.a>b?ac2>bc2.( )
4.a>b?a+c>b+c.( )
5. ?a+c>b+d.( )
思考辨析 判断正误
×
√
×
×
√
作商法
例题巩固
一、利用不等式的性质判断命题的真假
课本42页
方法总结
利用不等式性质判断命题真假的注意点
(1)运用不等式的性质判断时,要注意不等式成立的条件,不要弱化条件,尤其是不能凭想当然随意捏造性质.
(2)采用特殊值法进行排除,取值一定要遵循如下原则:
一是满足题设条件;二是取值要简单,便于验证计算.
例题巩固
一、利用不等式的性质判断命题的真假
课本57页
例题巩固
例. 已知2≤a≤3,-2≤b≤-1,则2a+b的取值范围是_____________.
二、利用不等式的性质求范围
∵4≤2a≤6,-2≤b≤-1
∴2≤2a+b≤5.
例. 已知2≤a≤3,-2≤b≤-1,则2a-b的取值范围是_____________.
∵-2≤b≤-1,∴ 1≤-b≤2.
4≤2a≤6,∴5≤2a-b≤8.
例题巩固
二、利用不等式的性质求范围
(延伸)已知0
反思感悟
利用不等式的性质求取值范围的策略
(1)建立待求范围的整体与已知范围的整体的关系,最后利用一次不等式的性质进行运算,求得待求的范围.
(2)同向(异向)不等式的两边可以相加(相减),这种转化不是等价变形,如果在解题过程中多次使用这种转化,就有可能扩大其取值范围.
注意:求解这种不等式问题要特别注意不能简单地分别求出单个变量的范围,再去求其他不等式的范围.
课堂练习
已知-1≤x+y≤4,2≤x-y≤3,则z=2x-3y的取值范围是_____________.
课堂小结
实际问题、
几何问题
不等关系
两个实数大小关系的基本事实(作差法)
不等式
不等式
性质
数学抽象
性质的应用
判断命题的真假
等式性质与不等式性质(2)
基本不等式
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
