四川省崇州市怀远中学2022-2023学年高三上学期开学考试数学(文科)试题(PDF无答案)
文档属性
| 名称 | 四川省崇州市怀远中学2022-2023学年高三上学期开学考试数学(文科)试题(PDF无答案) | 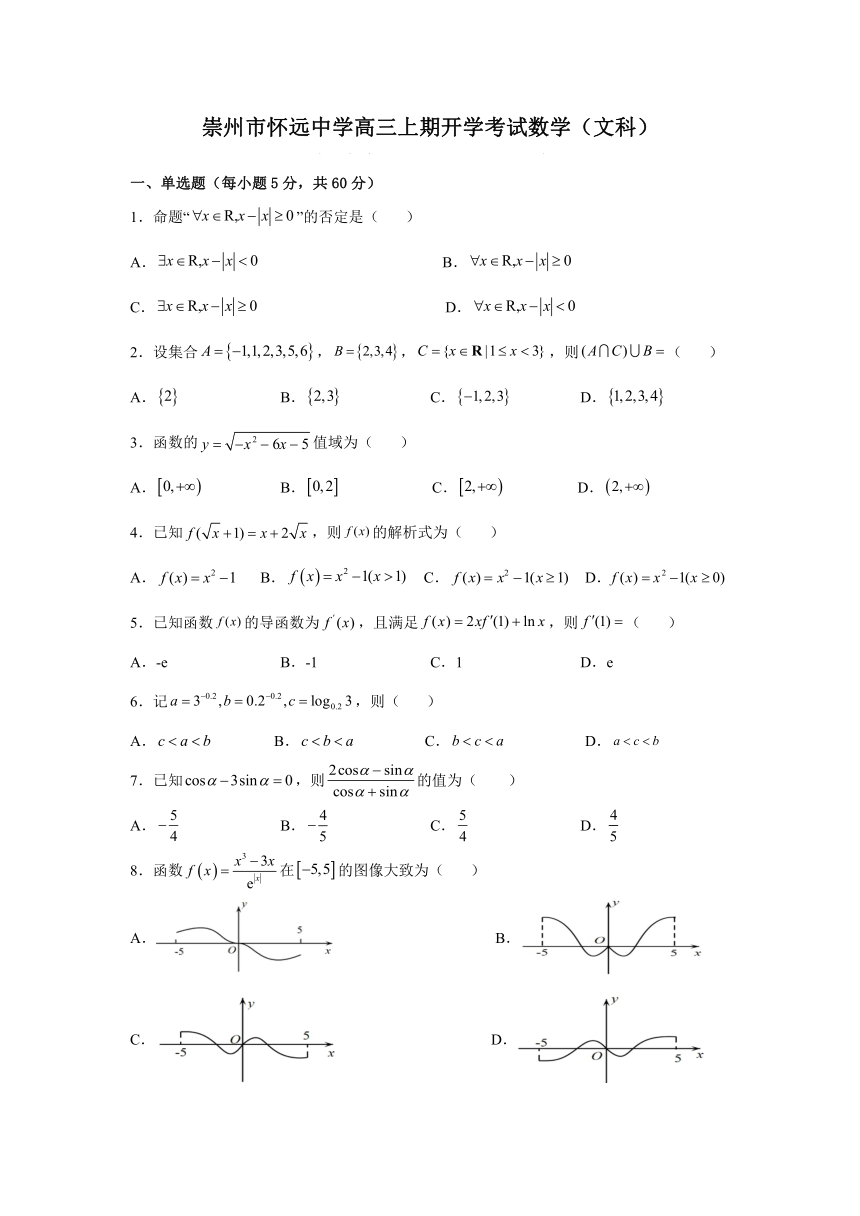 | |
| 格式 | |||
| 文件大小 | 251.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-24 14:26:05 | ||
图片预览


文档简介
崇州市怀远中学高三上期开学考试数学(文科)
出题人:童君 审题人:周芳
一、单选题(每小题 5 分,共 60 分)
1.命题“ x R,x x 0 ”的否定是( )
A. x R,x x 0 B. x R,x x 0
C. x R,x x 0 D. x R,x x 0
2.设集合 A 1,1,2,3,5,6 , B 2,3,4 ,C {x R |1 x 3},则 (A C) B ( )
A. 2 B. 2,3 C. 1, 2,3 D. 1,2,3,4
3.函数的 y x 2 6x 5值域为( )
A. 0, B. 0,2 C. 2, D. 2,
4.已知 f ( x 1) x 2 x ,则 f (x)的解析式为( )
A. f (x) x2 1 B. f x x2 1(x 1) C. f (x) x2 1(x 1) D.f (x) x 2 1(x 0)
5.已知函数 f (x)的导函数为 f (x),且满足 f (x) 2xf (1) ln x,则 f (1) ( )
A.-e B.-1 C.1 D.e
6 a 3 0.2.记 ,b 0.2 0.2 ,c log0.2 3,则( )
A.c a b B.c b a C.b c a D. a c b
2cos sin
7.已知cos 3sin 0,则 的值为( )
cos sin
5 4 5 4
A. B. C. D.
4 5 4 5
f x x
3 3x
8.函数 在 5,5x 的图像大致为( )e
A. B.
C. D.
9.函数 f x Asin x A 0, 0,
的部分图象如图,则 f ( )的值为2 ( ) 2
A 6 3 2. B. C. D. 1
2 2 2
10.已知 f (x)是定义域为 ( , )的奇函数,满足 f (x) f (2 x).若 f (1) 1,则
f (1) f (2) f (3) f (4) f (30) ( )
A.13 B.0 C. 1 D.1
f x 2sin 1 x 11.已知函数 ,直线 x 为 f x 图象的一条对称轴,则下
3 2
列说法正确的是( )
π f x , A. B. 在区间
单调递减
6 2
C. f x 在区间 , 上的最大值为 2 D. f x 为偶函数,则 2 3k k Z
12 f (x).已知定义在R 上的偶函数 y f (x)的导函数为 y f (x),当 x 0时, f (x) 0,
x
且 f (2) 3,则不等式 f (2x 1)
6
的解集为( )
2x 1
1 3 3
A . , , B. ,
2 2 2
1 , 3 1 1 1 3 C. D. , ,
2 2 2 2 2 2
二、填空题(每小题 5 分,共 20 分)
13.若不等式 x a的一个充分条件为 2 x 0,则实数 a的取值范围是___________.
14.求曲线 y f x 2x 2 3在点 2,8 处的切线与 x轴、直线 x=2所围成的三角形的面
积是 .
15 2.已知 f x 2cos x sin x 3 sin x cos x sin x,则函数 y f x 的单调递增区
6
间 .
ex
16.函数 f (x) 2t
1
ln x 2x 恰有两个极值点,则实数 t的取值范围是_________.x x
三、解答题(解答题需写出必要的解题过程,只写答案不给分)
17 f x x3.已知函数 x2 ax b,若曲线 y f x 在 0, f 0 处的切线方程为 y x 1.
(1)求 a,b的值;
(2)求函数 y f x 在 2,2 上的最值.
18.2021年秋季学期,某省在高一推进新教材,为此该省某市教育部门组织该市全体高中
教师在暑假期间进行相关学科培训,培训后举行测试(满分 100分),从该市参加测试的数
学老师中抽取了 100名老师并统计他们的测试分数,将成绩分成五组,第一组[65,70),第
二组[70,75),第三组[75,80),第四组[80,85),第五组[85,90],得到如图所示的频率
分布直方图.
(1)求 a的值以及这 100人中测试成绩在[80,85)的人数;
(2)估计全市老师测试成绩的平均数和中位数(保留两位小数);
(3)若从第三、四、五组老师中用分层抽样的方法抽取 6人作学习心得交流分享,并在这 6
人中再抽取 2人担当分享交流活动的主持人,求第四组至少有 1名老师被抽到的概率.
19.已知函数 f (x) cos x( 3 sin x
1
cos x) .
2
(1)求 f x 的最小正周期;
(2)在△ ABC中,角 A,B,C的对边分别为 a,b,c,若 f (C)
1
,c 2 3,sin A 2sin B,
2
求△ ABC的周长.
20.如图,在直三棱柱 ABC-A1B1C1中,AC=BC=CC1=2, ACB ,点 D为 BC中点.2
(1)求证:平面 A1CB⊥平面 AC1D;
(2)求点 C到平面 AC1D的距离.
3
21 x.设函数 f x ax a R .
6
(1)当a 2时,求函数 f (x)的极值;
(2)讨论函数 f (x)的单调性;
(3)设函数 g(x) f (x) a,直线 l与曲线 y ln x(0 x 1)及 y g(x)都相切,且 l与 y g(x)
切点的横坐标为 t,求证: 3 t 2 .
x 2 3t
22.在平面直角坐标系 xOy中,直线 l的参数方程为 (t为参数),以坐标原点 O
y t
为极点,x轴非负半轴为极轴建立极坐标系,曲线 C极坐标方程为: sin2 6cos .
(1)求直线 l普通方程与曲线 C的直角坐标方程;
(2) M 2,0 AM BM过点 的直线 l与 C相交于 A,B两点,求 的值.
出题人:童君 审题人:周芳
一、单选题(每小题 5 分,共 60 分)
1.命题“ x R,x x 0 ”的否定是( )
A. x R,x x 0 B. x R,x x 0
C. x R,x x 0 D. x R,x x 0
2.设集合 A 1,1,2,3,5,6 , B 2,3,4 ,C {x R |1 x 3},则 (A C) B ( )
A. 2 B. 2,3 C. 1, 2,3 D. 1,2,3,4
3.函数的 y x 2 6x 5值域为( )
A. 0, B. 0,2 C. 2, D. 2,
4.已知 f ( x 1) x 2 x ,则 f (x)的解析式为( )
A. f (x) x2 1 B. f x x2 1(x 1) C. f (x) x2 1(x 1) D.f (x) x 2 1(x 0)
5.已知函数 f (x)的导函数为 f (x),且满足 f (x) 2xf (1) ln x,则 f (1) ( )
A.-e B.-1 C.1 D.e
6 a 3 0.2.记 ,b 0.2 0.2 ,c log0.2 3,则( )
A.c a b B.c b a C.b c a D. a c b
2cos sin
7.已知cos 3sin 0,则 的值为( )
cos sin
5 4 5 4
A. B. C. D.
4 5 4 5
f x x
3 3x
8.函数 在 5,5x 的图像大致为( )e
A. B.
C. D.
9.函数 f x Asin x A 0, 0,
的部分图象如图,则 f ( )的值为2 ( ) 2
A 6 3 2. B. C. D. 1
2 2 2
10.已知 f (x)是定义域为 ( , )的奇函数,满足 f (x) f (2 x).若 f (1) 1,则
f (1) f (2) f (3) f (4) f (30) ( )
A.13 B.0 C. 1 D.1
f x 2sin 1 x 11.已知函数 ,直线 x 为 f x 图象的一条对称轴,则下
3 2
列说法正确的是( )
π f x , A. B. 在区间
单调递减
6 2
C. f x 在区间 , 上的最大值为 2 D. f x 为偶函数,则 2 3k k Z
12 f (x).已知定义在R 上的偶函数 y f (x)的导函数为 y f (x),当 x 0时, f (x) 0,
x
且 f (2) 3,则不等式 f (2x 1)
6
的解集为( )
2x 1
1 3 3
A . , , B. ,
2 2 2
1 , 3 1 1 1 3 C. D. , ,
2 2 2 2 2 2
二、填空题(每小题 5 分,共 20 分)
13.若不等式 x a的一个充分条件为 2 x 0,则实数 a的取值范围是___________.
14.求曲线 y f x 2x 2 3在点 2,8 处的切线与 x轴、直线 x=2所围成的三角形的面
积是 .
15 2.已知 f x 2cos x sin x 3 sin x cos x sin x,则函数 y f x 的单调递增区
6
间 .
ex
16.函数 f (x) 2t
1
ln x 2x 恰有两个极值点,则实数 t的取值范围是_________.x x
三、解答题(解答题需写出必要的解题过程,只写答案不给分)
17 f x x3.已知函数 x2 ax b,若曲线 y f x 在 0, f 0 处的切线方程为 y x 1.
(1)求 a,b的值;
(2)求函数 y f x 在 2,2 上的最值.
18.2021年秋季学期,某省在高一推进新教材,为此该省某市教育部门组织该市全体高中
教师在暑假期间进行相关学科培训,培训后举行测试(满分 100分),从该市参加测试的数
学老师中抽取了 100名老师并统计他们的测试分数,将成绩分成五组,第一组[65,70),第
二组[70,75),第三组[75,80),第四组[80,85),第五组[85,90],得到如图所示的频率
分布直方图.
(1)求 a的值以及这 100人中测试成绩在[80,85)的人数;
(2)估计全市老师测试成绩的平均数和中位数(保留两位小数);
(3)若从第三、四、五组老师中用分层抽样的方法抽取 6人作学习心得交流分享,并在这 6
人中再抽取 2人担当分享交流活动的主持人,求第四组至少有 1名老师被抽到的概率.
19.已知函数 f (x) cos x( 3 sin x
1
cos x) .
2
(1)求 f x 的最小正周期;
(2)在△ ABC中,角 A,B,C的对边分别为 a,b,c,若 f (C)
1
,c 2 3,sin A 2sin B,
2
求△ ABC的周长.
20.如图,在直三棱柱 ABC-A1B1C1中,AC=BC=CC1=2, ACB ,点 D为 BC中点.2
(1)求证:平面 A1CB⊥平面 AC1D;
(2)求点 C到平面 AC1D的距离.
3
21 x.设函数 f x ax a R .
6
(1)当a 2时,求函数 f (x)的极值;
(2)讨论函数 f (x)的单调性;
(3)设函数 g(x) f (x) a,直线 l与曲线 y ln x(0 x 1)及 y g(x)都相切,且 l与 y g(x)
切点的横坐标为 t,求证: 3 t 2 .
x 2 3t
22.在平面直角坐标系 xOy中,直线 l的参数方程为 (t为参数),以坐标原点 O
y t
为极点,x轴非负半轴为极轴建立极坐标系,曲线 C极坐标方程为: sin2 6cos .
(1)求直线 l普通方程与曲线 C的直角坐标方程;
(2) M 2,0 AM BM过点 的直线 l与 C相交于 A,B两点,求 的值.
同课章节目录
