苏科版七年级上册4.2 解一元一次方程课件(共17张PPT)
文档属性
| 名称 | 苏科版七年级上册4.2 解一元一次方程课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 557.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-24 17:18:40 | ||
图片预览




文档简介
(共17张PPT)
初中数学七年级上册
(苏科版)
4.2 解一元一次方程
如图,设天平左盘每个蓝色小球的质量为xg,天平平衡时可列方程 。
问题一:
1.创设情境,引入新课
2x+1=5
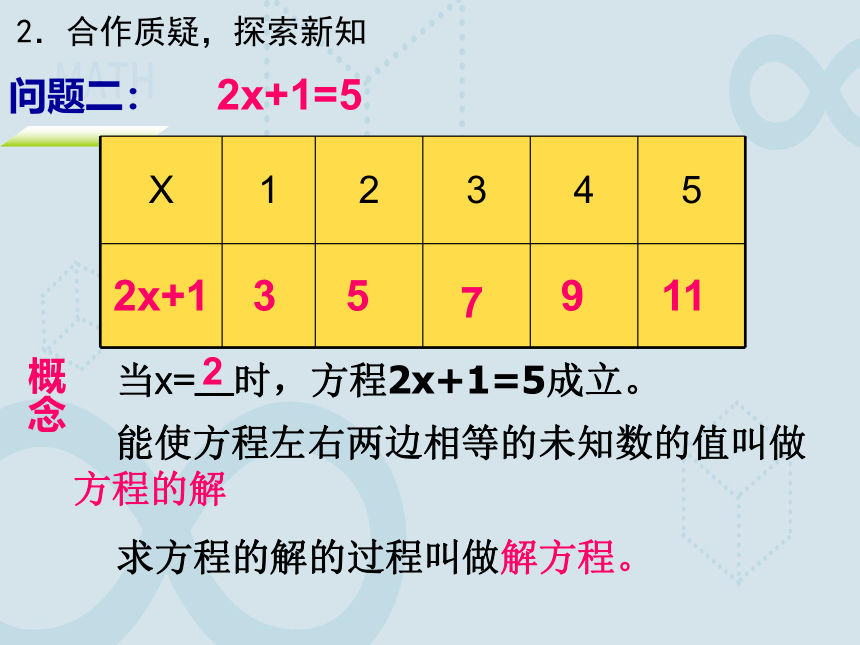
问题二:
2.合作质疑,探索新知
X 1 2 3 4 5
2x+1
当x=__时,方程2x+1=5成立。
3
5
7
9
11
2
能使方程左右两边相等的未知数的值叫做方程的解
求方程的解的过程叫做解方程。
概念
2x+1=5
例1:检验下列各数是否为方程2x-7=5-4x的解
(1)3 (2)2
练一练:检验下列各数是否为方程-x-7=4x+8的解
(1)3 (2)2
解(1)把x=3代入方程得:
方程左边=2×3-7= 6 – 7 = - 1
右边=5 - 4×3=5 – 12= - 7
∵左边≠右边 ,
∴x=3不是方程2x-7=5- 4x的解
检验一个数是不是方程的解的步骤:
1.将数值代入方程左边进行计算,
2.将数值代入方程右边进行计算,
3.比较左右两边的值,若左边=右边,则是方程的解,反之,则不是.
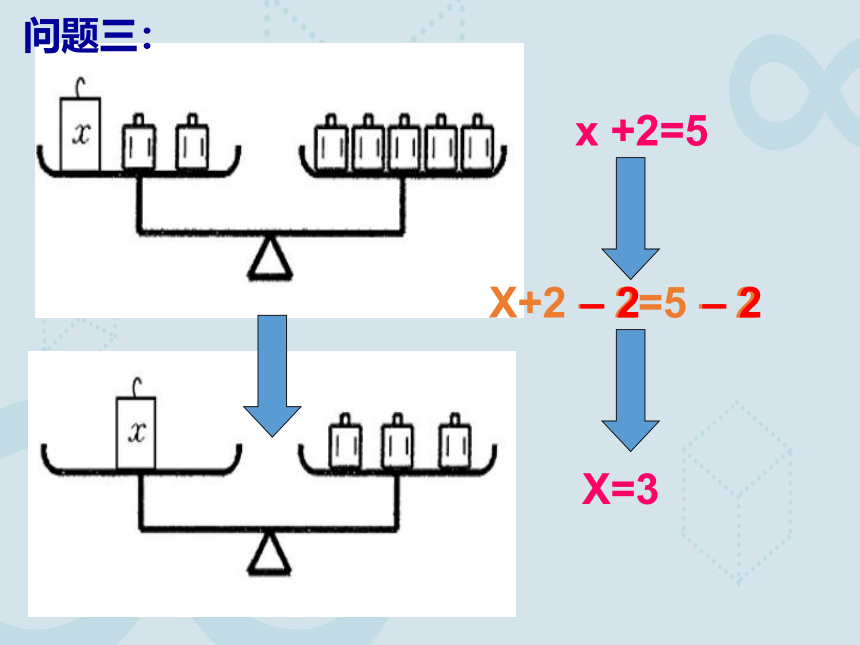
问题三:
x +2=5
X=3
X+2 – 2=5 – 2
– 2
– 2
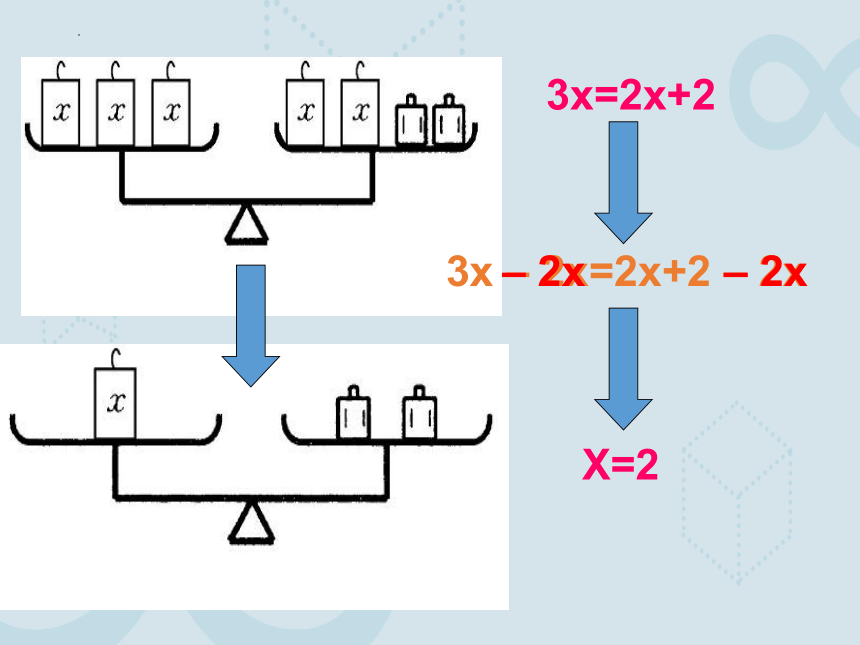
3x=2x+2
X=2
3x – 2x=2x+2 – 2x
– 2x
– 2x
2x=6
X=3
2
2
x +2=5
X+2 – 2=5 – 2
3x=2x+2
3x – 2x=2x+2 – 2x
2x=6
你能用语言描述等式的这些性质吗?
等式的基本性质:
(1)等式两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式;
(2)等式两边都乘(或除以)同一个不等于0的数,所得结果仍是等式.
如果 a = b,那么 a ± c = b ± c
如果 a = b,那么 a c = b c
如果 a = b,那么 (c≠ 0)
1.若x-5=3,则x=3+____,这是根据等式的性质___,在等式的两边都_____________.
2.若7=-3x+4,则7+___=4,这是根据等式的性质___,在等式的两边都_____________.
3.若 =-6,则2 =-6×___,这是根据等式的性质___,在等式的两边都___________.
4.若-4x=20,则____=-5,这是根据等式的性质___,在等式的两边都_____________.
小试牛刀
5
1
加上5
3x
1
加上3x
3
2
乘以3
x
2
除以-4
5.判断下列变形是否正确?
(1)由 x+5 = y+5 ,得 x = y ( )
(2)由2x-1 = 4 ,得 2x = 5 ( )
(3)由2x = 1 ,得 x = 2 ( )
(4)由3x = 2x ,得 3= 2 ( )
(5)如果x=y,那么 ( )
a
5
y
a
5
x
-
=
-
×
√
√
×
×
(1) x 5 = 7 (2) 4x = 2x 4
例2:利用等式的性质解下列方程:
解:(1)两边都加上5得:x – 5 +5=7+5
合并同类项得:x=12
(2)两边都减去4x得:4x – 2x=2x – 4 – 2x
合并同类项得: 2x= - 4
两边都除以2得:x= - 2
解方程的实质
利用等式的性质将方程变形为x = a(a为常 数)的形式
(3)3x+4=0 (4) 7y + 6 = 6y
解:(3)两边都减去4得:3x+4 – 4=0 – 4
合并同类项得:3x= - 4
两边都除以3得:x=
(4)两边都加上6y – 6 得:
7y+6+(6y - 6)= - 6y+(6y - 6)
合并同类项得:13y= - 6
两边都除以13得:y=
性质:
(1)方程两边都加上或都减去同
一个数或同一个整式,方程的解不变;
(2)方程两边都乘以或都除以同一个不为零的数,方程的解不变。
利用等式性质,解下列方程
(1)-3x= 3-4x
(2) x = 3
(3)-6x +8= 2 – 3x
1
2
练习
4.课堂小结,感悟收获
1.方程的解
2.解方程
3.等式的性质
4.利用等式的性质解方程
从
问
题
到
方
程
初中数学七年级上册
(苏科版)
4.2 解一元一次方程
如图,设天平左盘每个蓝色小球的质量为xg,天平平衡时可列方程 。
问题一:
1.创设情境,引入新课
2x+1=5
问题二:
2.合作质疑,探索新知
X 1 2 3 4 5
2x+1
当x=__时,方程2x+1=5成立。
3
5
7
9
11
2
能使方程左右两边相等的未知数的值叫做方程的解
求方程的解的过程叫做解方程。
概念
2x+1=5
例1:检验下列各数是否为方程2x-7=5-4x的解
(1)3 (2)2
练一练:检验下列各数是否为方程-x-7=4x+8的解
(1)3 (2)2
解(1)把x=3代入方程得:
方程左边=2×3-7= 6 – 7 = - 1
右边=5 - 4×3=5 – 12= - 7
∵左边≠右边 ,
∴x=3不是方程2x-7=5- 4x的解
检验一个数是不是方程的解的步骤:
1.将数值代入方程左边进行计算,
2.将数值代入方程右边进行计算,
3.比较左右两边的值,若左边=右边,则是方程的解,反之,则不是.
问题三:
x +2=5
X=3
X+2 – 2=5 – 2
– 2
– 2
3x=2x+2
X=2
3x – 2x=2x+2 – 2x
– 2x
– 2x
2x=6
X=3
2
2
x +2=5
X+2 – 2=5 – 2
3x=2x+2
3x – 2x=2x+2 – 2x
2x=6
你能用语言描述等式的这些性质吗?
等式的基本性质:
(1)等式两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式;
(2)等式两边都乘(或除以)同一个不等于0的数,所得结果仍是等式.
如果 a = b,那么 a ± c = b ± c
如果 a = b,那么 a c = b c
如果 a = b,那么 (c≠ 0)
1.若x-5=3,则x=3+____,这是根据等式的性质___,在等式的两边都_____________.
2.若7=-3x+4,则7+___=4,这是根据等式的性质___,在等式的两边都_____________.
3.若 =-6,则2 =-6×___,这是根据等式的性质___,在等式的两边都___________.
4.若-4x=20,则____=-5,这是根据等式的性质___,在等式的两边都_____________.
小试牛刀
5
1
加上5
3x
1
加上3x
3
2
乘以3
x
2
除以-4
5.判断下列变形是否正确?
(1)由 x+5 = y+5 ,得 x = y ( )
(2)由2x-1 = 4 ,得 2x = 5 ( )
(3)由2x = 1 ,得 x = 2 ( )
(4)由3x = 2x ,得 3= 2 ( )
(5)如果x=y,那么 ( )
a
5
y
a
5
x
-
=
-
×
√
√
×
×
(1) x 5 = 7 (2) 4x = 2x 4
例2:利用等式的性质解下列方程:
解:(1)两边都加上5得:x – 5 +5=7+5
合并同类项得:x=12
(2)两边都减去4x得:4x – 2x=2x – 4 – 2x
合并同类项得: 2x= - 4
两边都除以2得:x= - 2
解方程的实质
利用等式的性质将方程变形为x = a(a为常 数)的形式
(3)3x+4=0 (4) 7y + 6 = 6y
解:(3)两边都减去4得:3x+4 – 4=0 – 4
合并同类项得:3x= - 4
两边都除以3得:x=
(4)两边都加上6y – 6 得:
7y+6+(6y - 6)= - 6y+(6y - 6)
合并同类项得:13y= - 6
两边都除以13得:y=
性质:
(1)方程两边都加上或都减去同
一个数或同一个整式,方程的解不变;
(2)方程两边都乘以或都除以同一个不为零的数,方程的解不变。
利用等式性质,解下列方程
(1)-3x= 3-4x
(2) x = 3
(3)-6x +8= 2 – 3x
1
2
练习
4.课堂小结,感悟收获
1.方程的解
2.解方程
3.等式的性质
4.利用等式的性质解方程
从
问
题
到
方
程
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
