沪科版(2012)八年级数学上册第12章一次函数单元测试卷(附答案解析)
文档属性
| 名称 | 沪科版(2012)八年级数学上册第12章一次函数单元测试卷(附答案解析) | 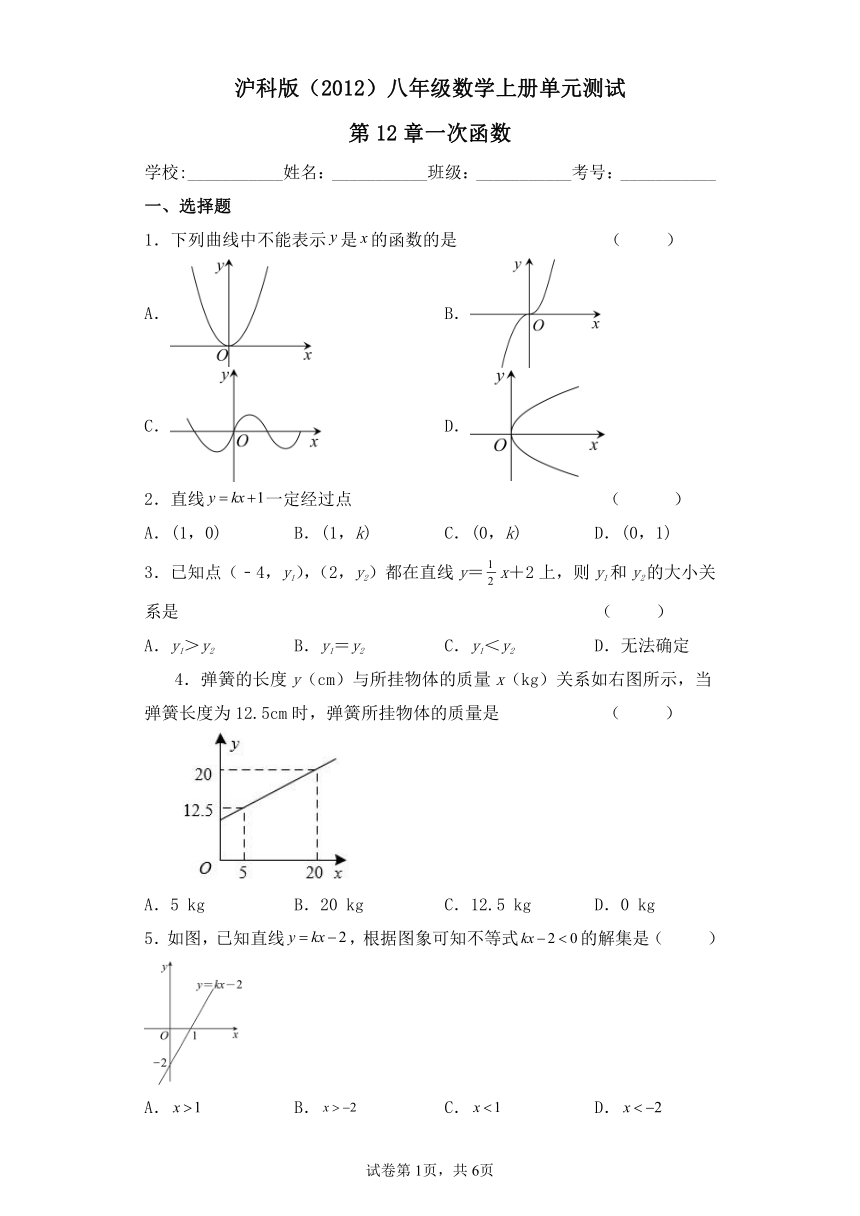 | |
| 格式 | zip | ||
| 文件大小 | 850.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-24 20:25:51 | ||
图片预览




文档简介
沪科版(2012)八年级数学上册单元测试
第12章一次函数
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下列曲线中不能表示是的函数的是 ( )
A. B.
C. D.
2.直线一定经过点 ( )
A.(1,0) B.(1,k) C.(0,k) D.(0,1)
3.已知点(﹣4,y1),(2,y2)都在直线y=x+2上,则y1和y2的大小关系是 ( )
A.y1>y2 B.y1=y2 C.y1<y2 D.无法确定
4.弹簧的长度y(cm)与所挂物体的质量x(kg)关系如右图所示,当弹簧长度为12.5cm时,弹簧所挂物体的质量是 ( )
A.5 kg B.20 kg C.12.5 kg D.0 kg
5.如图,已知直线,根据图象可知不等式的解集是( )
A. B. C. D.
6.将直线向上平移3个单位长度后得到的直线的函数表达式是( )
A. B. C. D.
7.对于一次函数,下列说法不正确的是 ( )
A.图象与的图象平行 B.图象不经过第三象限
C.图象与坐标轴围成的面积是2 D.当时,
8.在平面直角坐标系内,一次函数与正比例函数的图像如图所示,则关于x、y的方程组的解是 ( )
A. B. C. D.
9.如图,甲、乙两人相约从张庄到李庄,甲骑自行车先行,乙开车,两人均在同一路线上匀速行驶,乙到李庄后即停车等甲,甲、乙两人之间的距离y(千米)与甲行驶的时间x(小时)之间的函数关系如图所示,则下列说法不正确的是 ( )
A.甲骑自行车的速度为10km/h
B.乙开车的速度为50km/h
C.乙从张庄到李庄所用的时间为0.25小时
D.当甲行驶1.25小时,乙追上了甲
10.把8个边长为1的正方形按如图所示摆放在直角坐标系中,经过原点O的直线l将这8个正方形分成面积相等的两部分,则该直线的函数表达式是
( )
A. B. C. D.
二、填空题
11.过点的正比例函数解析式是________
12.函数,当函数值为4时,自变量x的取值为________.
13.一次函数的图象与轴的交点坐标是______.
14.如图是骆驼一天内的体温随时间变化的函数图像,这一天中在_______时间范围内它的体温在上升.
15.弹簧的自然长度为,在弹簧的弹性限度内,所挂的物体的质量每增加,弹簧的长度增加,则与之间的函数关系式是:______.
16.已知一次函数的图象不经过第二象限,那么函数值随自变量的值增大而______ 填“增大”或“减小”.
17.已知一次函数的图象经过点,并与直线平行,那么这个一次函数解析式是______.
18.如图,在平面直角坐标系中,点在直线与直线之间,则m的取值范围是________.
三、解答题
19.已知y与x成正比例,且当x=3时,y=4
(1)求y与x之间的函数解析式;
(2)当x=﹣1时,求y的值.
20.已知直线y=kx+b的图象经过点(2,4)和点(﹣2,﹣2).
(1)求b的值;
(2)求关于x的方程kx+b=0的解.
21.金百超市经销某品牌童装,单价为每件50元时,每天销量为60件,当单价每件从50元降了20元时,一天销量为100件.设降x元时,一天的销量为y件.已知y是x的一次函数.
(1)求y与x之间的关系式;
(2)若某天销售童装80件,则该天童装的单价是多少
22.如图,点A,B,C在一次函数y=-2x+m的图象上,它们的横坐标依次为-1,1,2,分别过这些点作x轴与y轴的垂线,求图中阴影部分的面积之和.
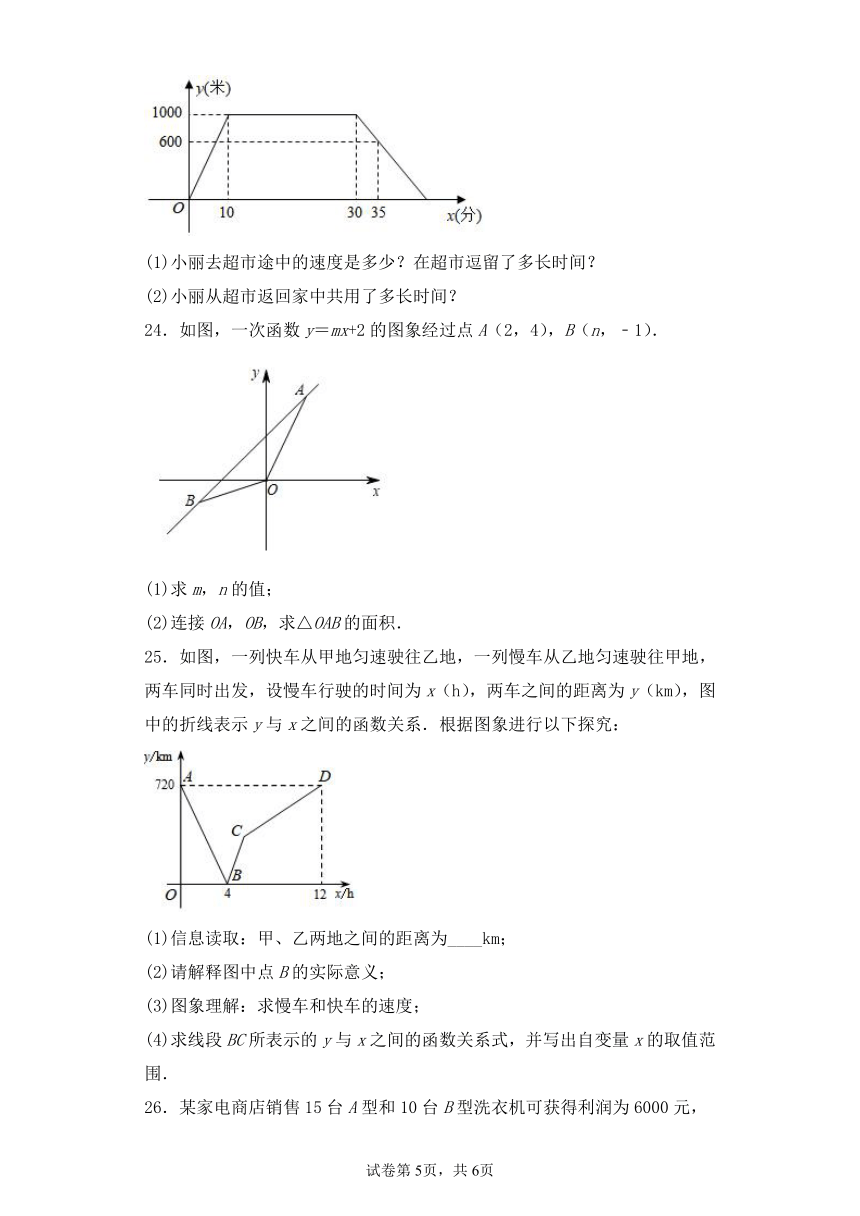
23.小丽从家里出发,步行去-家超市购物,然后从超市返回家中.小丽离家的路程y(米)和所经过的时间 x(分)之间的关系如图所示,请根据图象回答下列问题:
(1)小丽去超市途中的速度是多少?在超市逗留了多长时间?
(2)小丽从超市返回家中共用了多长时间?
24.如图,一次函数y=mx+2的图象经过点A(2,4),B(n,﹣1).
(1)求m,n的值;
(2)连接OA,OB,求△OAB的面积.
25.如图,一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
(1)信息读取:甲、乙两地之间的距离为____km;
(2)请解释图中点B的实际意义;
(3)图象理解:求慢车和快车的速度;
(4)求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围.
26.某家电商店销售15台A型和10台B型洗衣机可获得利润为6000元,销售10台A型和15台B型洗衣机的利润6500元.
(1)问A型和B型洗衣机每台的销售利润各是多少元.
(2)该商店计划一次购进两种型号的洗衣机共160台,其中B型洗衣机的进货量不超过A型洗衣机的2倍,设购进A型洗衣机为x台,这160台洗衣机的销售总利润为y元.
①求y与x之间的函数表达式;
②该商店购进A型、B型洗衣机各多少台,才能使销售利润最大?
27.如图,直线的解析式为,且与x轴交于点B,直线经过点A、D,直线、相交于点C.
(1)求点B坐标;
(2)求直线的解析式;
(3)求△ABC的面积;
(4)直线上存在异于点C的另一点P,使△ABP与△ABC的面积相等,请直接写出点P的坐标.
试卷第6页,共6页
试卷第5页,共6页
参考答案:
1.
【解析】A.当x取一个值时,y有唯一的一个值与x对应,故该选项能表示是的函数,不符合题意;
B.当x取一个值时,y有唯一的一个值与x对应,故该选项能表示是的函数,不符合题意;
C.当x取一个值时,y有唯一的一个值与x对应,故该选项能表示是的函数,不符合题意;
D.在图象中,在x轴正半轴上取一点,即确定一个x的值,这个x对应图象上两个点,即一个x的值有两个y值与之对应,故此图象不是y与x的函数图象,符合题意.
故选D.
2.
【解析】解: A、将x=1代入得:,不一定等于0,故本选项不符合题意;
B、将x=1代入得:,故本选项不符合题意;
C、将x=0代入得:,不一定等于k,故本选项不符合题意;
D、将x=0代入得:,故本选项符合题意;
故选D.
3.
【解析】解:∵点(﹣4,y1),(2,y2)都在直线y=x+2上,
∴y1=×(﹣4)+2=﹣2+2=0,y2=×2+2=1+2=3,
∵0<3,
∴y1<y2.
故选:C.
4.
【解析】解:由函数图象得:当y=12.5时,x=5,
∴当弹簧长度为12.5cm时,弹簧所挂物体的质量是5kg,
故选:A.
5.
【解析】解:根据图象可知当x<1时,直线落在x轴下方,
即不等式的解集是,故C正确.
故选:C.
6.
【解析】将直线y=x+1向上平移3个单位长度后得到的函数解析式是y=x+1+3=x+4,
故选:C.
7.
【解析】解:A、∵一次函数与一次函数中的k值相同,
∴一次函数与一次函数的图象平行,不符合题意;
B、∵一次函数中,,
∴一次函数的图象经过第一、二、四象限,不经过第三象限,不符合题意;
C、对于一次函数,当时,,当时,,
∴一次函数与坐标轴的交点坐标为(2,0),(0,2),
∴一次函数与坐标轴围成的图形面积为,不符合题意;
D、由函数图象可知当时,,符合题意;
故选D.
8.
【解析】解:∵一次函数与正比例函数的图象的交点坐标为(1,-1),
∴关于x、y的方程组的解是.
故选:C.
9.
【解析】解:由图象可得:甲骑自行车的速度为10÷1=10千米/小时,乙出发0.25小时追上甲,当甲行驶1.25小时,乙追上了甲.故A,D正确,不符合题意;
设乙速度为x千米/小时,
0.25x=1.25×10,
解得:x=50,
∴乙的速度为50千米/小时,故B正确,不符合题意.
设追上后到达B地的时间是y,
50y﹣10y=10,
解得:y=0.25,
∴乙从A地到B地所用的时间为0.25+0.25=0.5(小时),故C错误,符合题意.
故选:C.
10.
【解析】解:如图,设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,易知OB=3,
∵经过原点的一条直线l将这八个正方形分成面积相等的两部分,
∴,
而OB=3,
∴AB 3=5,
AB=,
∴A点坐标为(,3),
设直线方程为y=kx,
则3=k,
∴k=,
∴直线l解析式为y=x.
故选:A.
11.
【解析】解:设正比例函数的解析式为y=kx,
根据题意,得:2k=3,
解,得k=.
则它的函数解析式为y=x,
故答案为:y=x.
12.
【解析】函数值为4时,,
得到,
解得x=0.
故答案为:0.
13.
【解析】解:当时,,
解得:,
一次函数的图象与轴的交点坐标是.
故答案为:.
14.
【解析】解:由函数图像可知:这一天在4~16时,它的体温在上升.
故答案为4~16.
15.
【解析】解:由题意可得,
,
故答案为:.
16.
【解析】解:一次函数的图象不经过第二象限,
,.
∴函数值随自变量的值增大而增大,
故答案为:增大.
17.
【解析】∵一次函数的图象与直线平行,
∴,即,
∵图象经过点,
∴,即,
∴这个一次函数的解析式是:.
故答案为:.
18.
【解析】解:当点在直线上时,,
当点在直线上时,,
则,
故答案为:
19.
(1)∵y与x成正比例,
∴设y=kx,
∵当x=3时,y=4,
∴4=3k,解得k=,
∴y与x之间的函数关系式为y=x;
(2)解:把x=﹣1代入y=x得y=﹣;
20.
(1)根据题意得,
①+②得:,
解得:,
将代入①得,
解得,
∴方程组的解是:,
∴b的值为1;
(2)
∵,
∴一次函数解析式为,
∴令y=kx+b=0,即,
解得,
关于x的方程kx+b=0的解是.
21.
(1)因为y是x的一次函数.
所以,设y与x的函数关系式为y=kx+b,
由题意知,当x=0时, y=60 ;当x=20时, y= 100,
所以,
解之得:
所以y与x之间的关系式为y=2x+60 ;
(2)当y=80时,由80=2x+60,
解得x=10,
所以50- 10= 40(元),
所以该天童装的单价是每件40元.
22.
【解析】解:各点标注如图所示:
把代入得:,
,
同理可得:,
,
,
,
,
答:图中阴影部分的面积之和为3.
23.
(1)解:1000÷10=100(米/分),
30 10=20(分);
答:小丽去超市途中的速度是100米/分,在超市逗留了20分.
(2)解:(1000 600)÷(35 30)=80(米/分),
1000÷80=12.5(分),
答:小丽从超市返回家中共用了12.5分.
24.
(1)解:∵一次函数y=mx+2的图象经过点A(2,4),
∴2m+2=4,
解得m=1,
∴一次函数表达式为y=x+2,
∵一次函数y=x+2的图象经过点B(n,﹣1),
∴n+2=﹣1,
解得n=﹣3;
(2)解:如图,设直线AB与y轴的交点为C,
令x=0,则y=2,
所以点C的坐标为(0,2),
∴OC=2,
∴=×2×2+×2×3=2+3=5.
25.
(1)由题意,结合图象可得甲、乙两地之间的距离为720km;
故答案为:720;
(2)由点B的纵坐标为0,可得甲乙两车距离为零,
故图中点B的实际意义为:慢车行驶4小时两车相遇;
(3)慢车速度720÷12=60(km/h),
快车速度720÷4-60=120(km/h);
(4)720÷120=6(小时),
6﹣4=22×(120+60)=360(km),
故C(6,360),
设线段BC所表示的y与x之间的函数关系式为y=kx+b(k≠0),
把C(6,360),B(4,0)代入得:
,
解得,
∴y=180x﹣720(4≤x≤6).
26.
(1)设A型和B型洗衣机每台的销售利润各是a元和b元.
则,
解得:.
答:A型和B型洗衣机每台的销售利润各是200元和300元;
(2)①根据题意得y=200x+300(160-x),即y=-100x+48000;
②根据题意得:160-x≤2x,解得:x≥,
∵y=-100x+48000中,k=-100<0,
∴y随x的增大而减小.
∵x为正整数,
∴当x=54时,y取得最大值,此时160-x=106.
答:该商店购进A型、B型洗衣机各54台和106台时,才能使销售利润最大.
27.
(1)当y=0时, -2x+2=0,解得x=1
∴B(1,0)
(2)设的解析式为(k≠0)
∵直线过A(4,0),D(3,-1) ∴
∴ ∴
(3),解得
∴C(2,-2)
∵B(1,0),∴AB=4-1=3
∴
(4)在中令y=2可得x=6,
∴点P(6,2)即在上,
且.
答案第8页,共10页
答案第7页,共10页
第12章一次函数
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下列曲线中不能表示是的函数的是 ( )
A. B.
C. D.
2.直线一定经过点 ( )
A.(1,0) B.(1,k) C.(0,k) D.(0,1)
3.已知点(﹣4,y1),(2,y2)都在直线y=x+2上,则y1和y2的大小关系是 ( )
A.y1>y2 B.y1=y2 C.y1<y2 D.无法确定
4.弹簧的长度y(cm)与所挂物体的质量x(kg)关系如右图所示,当弹簧长度为12.5cm时,弹簧所挂物体的质量是 ( )
A.5 kg B.20 kg C.12.5 kg D.0 kg
5.如图,已知直线,根据图象可知不等式的解集是( )
A. B. C. D.
6.将直线向上平移3个单位长度后得到的直线的函数表达式是( )
A. B. C. D.
7.对于一次函数,下列说法不正确的是 ( )
A.图象与的图象平行 B.图象不经过第三象限
C.图象与坐标轴围成的面积是2 D.当时,
8.在平面直角坐标系内,一次函数与正比例函数的图像如图所示,则关于x、y的方程组的解是 ( )
A. B. C. D.
9.如图,甲、乙两人相约从张庄到李庄,甲骑自行车先行,乙开车,两人均在同一路线上匀速行驶,乙到李庄后即停车等甲,甲、乙两人之间的距离y(千米)与甲行驶的时间x(小时)之间的函数关系如图所示,则下列说法不正确的是 ( )
A.甲骑自行车的速度为10km/h
B.乙开车的速度为50km/h
C.乙从张庄到李庄所用的时间为0.25小时
D.当甲行驶1.25小时,乙追上了甲
10.把8个边长为1的正方形按如图所示摆放在直角坐标系中,经过原点O的直线l将这8个正方形分成面积相等的两部分,则该直线的函数表达式是
( )
A. B. C. D.
二、填空题
11.过点的正比例函数解析式是________
12.函数,当函数值为4时,自变量x的取值为________.
13.一次函数的图象与轴的交点坐标是______.
14.如图是骆驼一天内的体温随时间变化的函数图像,这一天中在_______时间范围内它的体温在上升.
15.弹簧的自然长度为,在弹簧的弹性限度内,所挂的物体的质量每增加,弹簧的长度增加,则与之间的函数关系式是:______.
16.已知一次函数的图象不经过第二象限,那么函数值随自变量的值增大而______ 填“增大”或“减小”.
17.已知一次函数的图象经过点,并与直线平行,那么这个一次函数解析式是______.
18.如图,在平面直角坐标系中,点在直线与直线之间,则m的取值范围是________.
三、解答题
19.已知y与x成正比例,且当x=3时,y=4
(1)求y与x之间的函数解析式;
(2)当x=﹣1时,求y的值.
20.已知直线y=kx+b的图象经过点(2,4)和点(﹣2,﹣2).
(1)求b的值;
(2)求关于x的方程kx+b=0的解.
21.金百超市经销某品牌童装,单价为每件50元时,每天销量为60件,当单价每件从50元降了20元时,一天销量为100件.设降x元时,一天的销量为y件.已知y是x的一次函数.
(1)求y与x之间的关系式;
(2)若某天销售童装80件,则该天童装的单价是多少
22.如图,点A,B,C在一次函数y=-2x+m的图象上,它们的横坐标依次为-1,1,2,分别过这些点作x轴与y轴的垂线,求图中阴影部分的面积之和.
23.小丽从家里出发,步行去-家超市购物,然后从超市返回家中.小丽离家的路程y(米)和所经过的时间 x(分)之间的关系如图所示,请根据图象回答下列问题:
(1)小丽去超市途中的速度是多少?在超市逗留了多长时间?
(2)小丽从超市返回家中共用了多长时间?
24.如图,一次函数y=mx+2的图象经过点A(2,4),B(n,﹣1).
(1)求m,n的值;
(2)连接OA,OB,求△OAB的面积.
25.如图,一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
(1)信息读取:甲、乙两地之间的距离为____km;
(2)请解释图中点B的实际意义;
(3)图象理解:求慢车和快车的速度;
(4)求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围.
26.某家电商店销售15台A型和10台B型洗衣机可获得利润为6000元,销售10台A型和15台B型洗衣机的利润6500元.
(1)问A型和B型洗衣机每台的销售利润各是多少元.
(2)该商店计划一次购进两种型号的洗衣机共160台,其中B型洗衣机的进货量不超过A型洗衣机的2倍,设购进A型洗衣机为x台,这160台洗衣机的销售总利润为y元.
①求y与x之间的函数表达式;
②该商店购进A型、B型洗衣机各多少台,才能使销售利润最大?
27.如图,直线的解析式为,且与x轴交于点B,直线经过点A、D,直线、相交于点C.
(1)求点B坐标;
(2)求直线的解析式;
(3)求△ABC的面积;
(4)直线上存在异于点C的另一点P,使△ABP与△ABC的面积相等,请直接写出点P的坐标.
试卷第6页,共6页
试卷第5页,共6页
参考答案:
1.
【解析】A.当x取一个值时,y有唯一的一个值与x对应,故该选项能表示是的函数,不符合题意;
B.当x取一个值时,y有唯一的一个值与x对应,故该选项能表示是的函数,不符合题意;
C.当x取一个值时,y有唯一的一个值与x对应,故该选项能表示是的函数,不符合题意;
D.在图象中,在x轴正半轴上取一点,即确定一个x的值,这个x对应图象上两个点,即一个x的值有两个y值与之对应,故此图象不是y与x的函数图象,符合题意.
故选D.
2.
【解析】解: A、将x=1代入得:,不一定等于0,故本选项不符合题意;
B、将x=1代入得:,故本选项不符合题意;
C、将x=0代入得:,不一定等于k,故本选项不符合题意;
D、将x=0代入得:,故本选项符合题意;
故选D.
3.
【解析】解:∵点(﹣4,y1),(2,y2)都在直线y=x+2上,
∴y1=×(﹣4)+2=﹣2+2=0,y2=×2+2=1+2=3,
∵0<3,
∴y1<y2.
故选:C.
4.
【解析】解:由函数图象得:当y=12.5时,x=5,
∴当弹簧长度为12.5cm时,弹簧所挂物体的质量是5kg,
故选:A.
5.
【解析】解:根据图象可知当x<1时,直线落在x轴下方,
即不等式的解集是,故C正确.
故选:C.
6.
【解析】将直线y=x+1向上平移3个单位长度后得到的函数解析式是y=x+1+3=x+4,
故选:C.
7.
【解析】解:A、∵一次函数与一次函数中的k值相同,
∴一次函数与一次函数的图象平行,不符合题意;
B、∵一次函数中,,
∴一次函数的图象经过第一、二、四象限,不经过第三象限,不符合题意;
C、对于一次函数,当时,,当时,,
∴一次函数与坐标轴的交点坐标为(2,0),(0,2),
∴一次函数与坐标轴围成的图形面积为,不符合题意;
D、由函数图象可知当时,,符合题意;
故选D.
8.
【解析】解:∵一次函数与正比例函数的图象的交点坐标为(1,-1),
∴关于x、y的方程组的解是.
故选:C.
9.
【解析】解:由图象可得:甲骑自行车的速度为10÷1=10千米/小时,乙出发0.25小时追上甲,当甲行驶1.25小时,乙追上了甲.故A,D正确,不符合题意;
设乙速度为x千米/小时,
0.25x=1.25×10,
解得:x=50,
∴乙的速度为50千米/小时,故B正确,不符合题意.
设追上后到达B地的时间是y,
50y﹣10y=10,
解得:y=0.25,
∴乙从A地到B地所用的时间为0.25+0.25=0.5(小时),故C错误,符合题意.
故选:C.
10.
【解析】解:如图,设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,易知OB=3,
∵经过原点的一条直线l将这八个正方形分成面积相等的两部分,
∴,
而OB=3,
∴AB 3=5,
AB=,
∴A点坐标为(,3),
设直线方程为y=kx,
则3=k,
∴k=,
∴直线l解析式为y=x.
故选:A.
11.
【解析】解:设正比例函数的解析式为y=kx,
根据题意,得:2k=3,
解,得k=.
则它的函数解析式为y=x,
故答案为:y=x.
12.
【解析】函数值为4时,,
得到,
解得x=0.
故答案为:0.
13.
【解析】解:当时,,
解得:,
一次函数的图象与轴的交点坐标是.
故答案为:.
14.
【解析】解:由函数图像可知:这一天在4~16时,它的体温在上升.
故答案为4~16.
15.
【解析】解:由题意可得,
,
故答案为:.
16.
【解析】解:一次函数的图象不经过第二象限,
,.
∴函数值随自变量的值增大而增大,
故答案为:增大.
17.
【解析】∵一次函数的图象与直线平行,
∴,即,
∵图象经过点,
∴,即,
∴这个一次函数的解析式是:.
故答案为:.
18.
【解析】解:当点在直线上时,,
当点在直线上时,,
则,
故答案为:
19.
(1)∵y与x成正比例,
∴设y=kx,
∵当x=3时,y=4,
∴4=3k,解得k=,
∴y与x之间的函数关系式为y=x;
(2)解:把x=﹣1代入y=x得y=﹣;
20.
(1)根据题意得,
①+②得:,
解得:,
将代入①得,
解得,
∴方程组的解是:,
∴b的值为1;
(2)
∵,
∴一次函数解析式为,
∴令y=kx+b=0,即,
解得,
关于x的方程kx+b=0的解是.
21.
(1)因为y是x的一次函数.
所以,设y与x的函数关系式为y=kx+b,
由题意知,当x=0时, y=60 ;当x=20时, y= 100,
所以,
解之得:
所以y与x之间的关系式为y=2x+60 ;
(2)当y=80时,由80=2x+60,
解得x=10,
所以50- 10= 40(元),
所以该天童装的单价是每件40元.
22.
【解析】解:各点标注如图所示:
把代入得:,
,
同理可得:,
,
,
,
,
答:图中阴影部分的面积之和为3.
23.
(1)解:1000÷10=100(米/分),
30 10=20(分);
答:小丽去超市途中的速度是100米/分,在超市逗留了20分.
(2)解:(1000 600)÷(35 30)=80(米/分),
1000÷80=12.5(分),
答:小丽从超市返回家中共用了12.5分.
24.
(1)解:∵一次函数y=mx+2的图象经过点A(2,4),
∴2m+2=4,
解得m=1,
∴一次函数表达式为y=x+2,
∵一次函数y=x+2的图象经过点B(n,﹣1),
∴n+2=﹣1,
解得n=﹣3;
(2)解:如图,设直线AB与y轴的交点为C,
令x=0,则y=2,
所以点C的坐标为(0,2),
∴OC=2,
∴=×2×2+×2×3=2+3=5.
25.
(1)由题意,结合图象可得甲、乙两地之间的距离为720km;
故答案为:720;
(2)由点B的纵坐标为0,可得甲乙两车距离为零,
故图中点B的实际意义为:慢车行驶4小时两车相遇;
(3)慢车速度720÷12=60(km/h),
快车速度720÷4-60=120(km/h);
(4)720÷120=6(小时),
6﹣4=22×(120+60)=360(km),
故C(6,360),
设线段BC所表示的y与x之间的函数关系式为y=kx+b(k≠0),
把C(6,360),B(4,0)代入得:
,
解得,
∴y=180x﹣720(4≤x≤6).
26.
(1)设A型和B型洗衣机每台的销售利润各是a元和b元.
则,
解得:.
答:A型和B型洗衣机每台的销售利润各是200元和300元;
(2)①根据题意得y=200x+300(160-x),即y=-100x+48000;
②根据题意得:160-x≤2x,解得:x≥,
∵y=-100x+48000中,k=-100<0,
∴y随x的增大而减小.
∵x为正整数,
∴当x=54时,y取得最大值,此时160-x=106.
答:该商店购进A型、B型洗衣机各54台和106台时,才能使销售利润最大.
27.
(1)当y=0时, -2x+2=0,解得x=1
∴B(1,0)
(2)设的解析式为(k≠0)
∵直线过A(4,0),D(3,-1) ∴
∴ ∴
(3),解得
∴C(2,-2)
∵B(1,0),∴AB=4-1=3
∴
(4)在中令y=2可得x=6,
∴点P(6,2)即在上,
且.
答案第8页,共10页
答案第7页,共10页
