苏教版数学六年级上册第一单元 同步练习(共4课时 含答案)
文档属性
| 名称 | 苏教版数学六年级上册第一单元 同步练习(共4课时 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 293.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-24 17:21:47 | ||
图片预览



文档简介
第一课时 长方体和正方体的认识
1.填一填。
(1)从不同角度观察同一个长方体,最多能同时看到( )个面,最少能看到( )个面。
(2)围成长方体的每一个长方形叫作长方体的( );长方体两个面相交的线叫作长方体的( );三条棱相交的点叫作长方体的( )。在图中标出来。
(3)长方体和正方体都有( )个面,( )条棱和( )个顶点。
(4)长方体的面是( ),也可能有2个相对的面是正方形,相对的面( ),相对的棱( )。
(5)正方体的6个面是完全相同的( ),12条棱长度( )。它是一种特殊的( )。
长方体的长、宽、高和正方体的棱长
2.先观察图形,再填空。
(1)图①是( )体,长、宽、高分别是( )米、( )米、( )米。它的上面的面是( )形,面积是( )平方米;左面的面是( )形,面积是( )平方米;后面的面的长和宽分别是( )米、( )米,面积是( )平方米。它有( )个完全相同的长方形,最多有( )条棱长度相等。
(2)图②是( )体,它的棱长是( )分米,它的( )个面完全相同。
3.(易错题)判断。(对的画“√”,错的画“ × ”)
(1)有四个面是完全一样的正方形的长方体一定是正方体。
(2)有8个顶点,6个面,12条棱的图形不是长方体就是正方体。
4.一个长方体礼品盒如下图。现在用一根彩带将它捆扎起来,这根彩带至少长多少分米
(打结处长3 dm)
5.用两个完全一样的正方体拼成一个长方体,棱长之和减少了32 cm。原来一个正方体的棱长和是多少
正方体、长方体的展开图
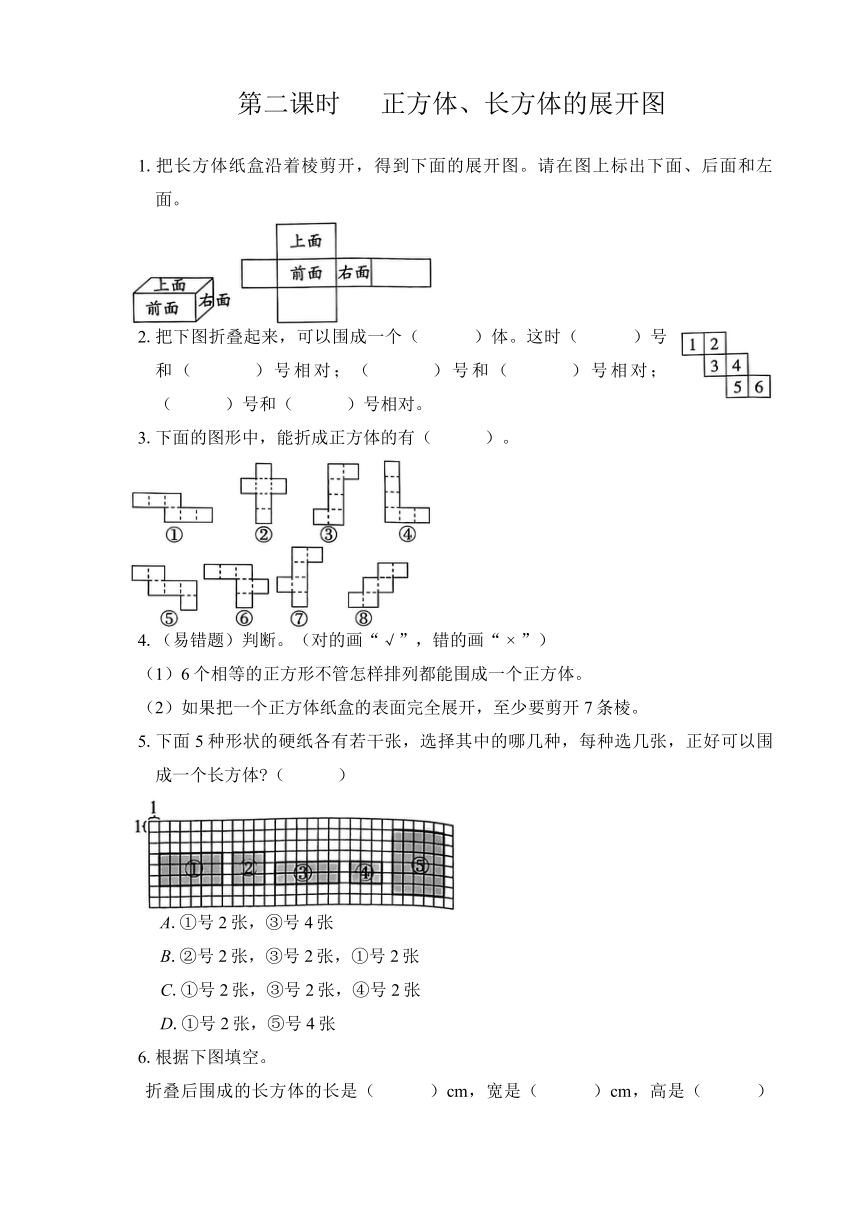
1.把长方体纸盒沿着棱剪开,得到下面的展开图。请在图上标出下面、后面和左面。
2.把下图折叠起来,可以围成一个( )体。这时( )号和( )号相对;( )号和( )号相对;( )号和( )号相对。
3.下面的图形中,能折成正方体的有( )。
4.(易错题)判断。(对的画“√”,错的画“ × ”)
(1)6个相等的正方形不管怎样排列都能围成一个正方体。
(2)如果把一个正方体纸盒的表面完全展开,至少要剪开7条棱。
5.下面5种形状的硬纸各有若干张,选择其中的哪几种,每种选几张,正好可以围成一个长方体 ( )
A.①号2张,③号4张
B.②号2张,③号2张,①号2张
C.①号2张,③号2张,④号2张
D.①号2张,⑤号4张
6.根据下图填空。
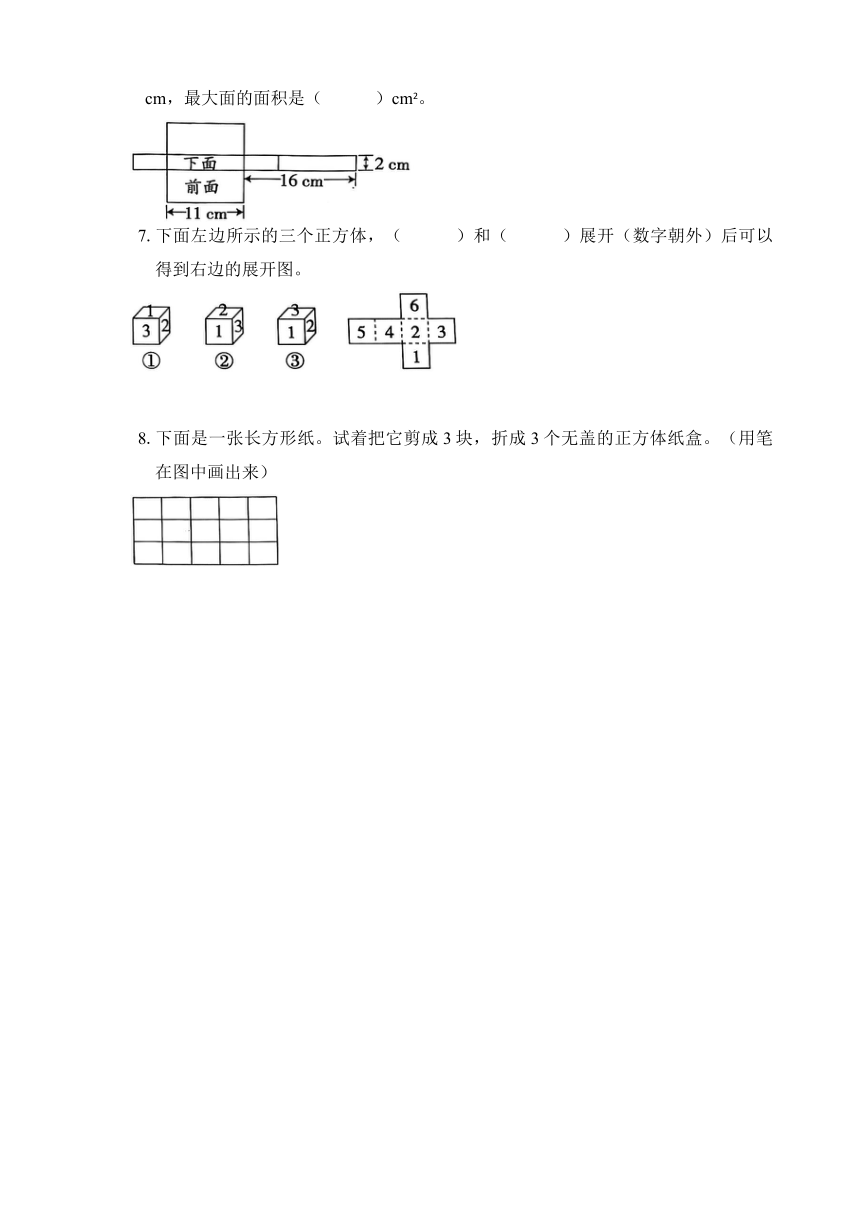
折叠后围成的长方体的长是( )cm,宽是( )cm,高是( )cm,最大面的面积是( )cm2。
7.下面左边所示的三个正方体,( )和( )展开(数字朝外)后可以得到右边的展开图。
8.下面是一张长方形纸。试着把它剪成3块,折成3个无盖的正方体纸盒。(用笔在图中画出来)
第三课时 长方体表面积的意义及计算方法
1.填一填。
(1)长方体(或正方体)( )个面的总面积,叫作它的表面积。
(2)一个长方体纸盒(如图),做这个纸盒需要多少平方厘米的硬纸板
①上面的面积: _________ ;②前面的面积: _________ ;③左面的面积: _________ ;表面积:( _________ + _________ + _________ ) × 2 = _________
答:做这个纸盒需要 _________ cm2的硬纸板。
2.一个长方体铁皮水箱,长和宽都是7 dm,深8 dm。做这样一个水箱至少需要铁皮多少平方分米 (水箱有盖)
3.计算下面正方体的表面积。
(1)每个面的面积:
(2)正方体的表面积:
_________ × 6 = _________
4.张师傅要给一个棱长为3 dm的正方体木箱喷漆,喷漆的面积是多少平方分米
5.(易错题)填一填。
(1)一个正方体的棱长扩大到原来的3倍,它的表面积扩大到原来的( )倍。
(2)一个长方体的长、宽、高分别扩大到原来的4倍,它的表面积扩大到原来的( )倍。
6.把1个正方体木块锯成3个完全一样的长方体,表面积增加了18 cm2,原来这个正方体木块的表面积是多少平方厘米
7.如图,有两个一样的长方体饼干盒,用包装纸将它们全封闭包装在一起拼成一个新的长方体。请你设计出3种方案,写出所拼成的长方体的长、宽、高,再计算出每种方案拼成的长方体的表面积。
第四课时 长方体和正方体表面积的计算
1.填一填。
(1)一个长方体鱼缸,长8分米,宽5分米,高6分米,前面的玻璃打破了,修理时配的玻璃的面积是( )平方分米。
(2)一个长方体游泳池,长50米,宽20米,深1.5米。给这个游泳池的四壁及底面贴上瓷砖,贴瓷砖的面积是( )个面的面积和,是( )平方米。
2.生产一个如图所示的长方体手提袋(无盖),至少需要多少平方分米的材料
3.(易错题)一根长2米的通风管,横截面是周长为8分米的正方形,现要制作4根这样的通风管,至少需要铁皮多少平方分米
4.如图是牙膏盒的直观图。做这个牙膏盒至少需要多少平方厘米的硬纸板
5.一个底面是正方形的长方体铁箱,如果把它的侧面展开,正好是一个边长为40厘米的正方形。这个铁箱的表面积是多少平方厘米
6.电影院大门前有6级台阶,每级台阶长6米,宽0.3米,高0.2米。
(1)6级台阶一共占地多少平方米
(2)给这些台阶铺地毯,至少需要多少平方米的地毯
一个长方体的底面是边长为2分米的正方形,长方体的高为4分米,如果把它的高增加5厘米,它的表面积会增加多少平方厘米
答案
第1课时长方体和正方体的认识
(1)3 1
(2)面 棱 顶点 填图略
(3)6 12 8
(4)长方形 完全相同 长度相等
(5)正方形 相等 长方体
2.(1)长方 2 0.5 0.5 长方 1
正方 0.25 2 0.5 1 4 8
(2)正方 5 6
3.(1)√(2) ×
4.8 × 2 + 8 × 2 + 3 × 4 + 3 = 47(dm)答:这根彩带至少长47 dm。
5.5.32 ÷ 8 × 12 = 48(cm)
答:原来一个正方体的棱长和是48 cm。
第2课时长方体和正方体的展开图
2.正方 1 4 2 5 3 6
3.①②③⑤⑦⑧
4.(1) × (2)√
5.C
6.11 2 5 55
7.①②
8.
(答案不唯一)
第3课时长方体和正方体表面积的计算
1.(1)6
(2)①10 × 6 = 60(cm2)
②10 × 4 = 40(cm2) ③4 × 6 = 24(cm2)
60 40 24 248(cm2) 248
2.7 × 7 × 2 + 7 × 8 × 4 = 322(dm2)
答:做这样一个水箱至少需要铁皮322 dm2。
3.(1)4 × 4 = 16(dm2)
(2)16 96(dm2)
4.3 × 3 × 6 = 54(dm2)
答:喷漆的面积是54 dm2。
5.(1)9(2)16
6.18 ÷ 4 × 6 = 27(cm2)
答:原来这个正方体木块的表面积是27 cm2。
7.10 6 4 248 20 6 2 344
12 10 2 328
第4课时长方体和正方体表面积的计算
1.(1)48(2)5 1210
2.(3 × 4 + 0.8 × 4) × 2 + 3 × 0.8 = 32.8(平方分米)
答:至少需要32.8平方分米的材料。
3.8 ÷ 4 = 2(分米) 2米 = 20分米
2 × 20 × 4 × 4 = 640(平方分米)
答:至少需要铁皮640平方分米。
4.5 × 5 × 2 + 5 × 18 × 4 = 410(cm2)
答:做这个牙膏盒至少需要410 cm2的硬纸板。
5.40 ÷ 4 = 10(厘米)
40 × 10 × 4 + 10 × 10 × 2 = 1800(平方厘米)答:这个铁箱的表面积是1800平方厘米。
6.(1)6 × 0.3 × 6 = 10.8(平方米)答:6级台阶一共占地10.8平方米。
(2)(6 × 0.3 + 6 × 0.2) × 6 = 18(平方米)答:至少需要18平方米的地毯。
7.2分米 = 20厘米 7.2分米 = 20厘米20 × 5 × 4 = 400(平方厘米)
答:它的表面积会增加400平方厘米。
1.填一填。
(1)从不同角度观察同一个长方体,最多能同时看到( )个面,最少能看到( )个面。
(2)围成长方体的每一个长方形叫作长方体的( );长方体两个面相交的线叫作长方体的( );三条棱相交的点叫作长方体的( )。在图中标出来。
(3)长方体和正方体都有( )个面,( )条棱和( )个顶点。
(4)长方体的面是( ),也可能有2个相对的面是正方形,相对的面( ),相对的棱( )。
(5)正方体的6个面是完全相同的( ),12条棱长度( )。它是一种特殊的( )。
长方体的长、宽、高和正方体的棱长
2.先观察图形,再填空。
(1)图①是( )体,长、宽、高分别是( )米、( )米、( )米。它的上面的面是( )形,面积是( )平方米;左面的面是( )形,面积是( )平方米;后面的面的长和宽分别是( )米、( )米,面积是( )平方米。它有( )个完全相同的长方形,最多有( )条棱长度相等。
(2)图②是( )体,它的棱长是( )分米,它的( )个面完全相同。
3.(易错题)判断。(对的画“√”,错的画“ × ”)
(1)有四个面是完全一样的正方形的长方体一定是正方体。
(2)有8个顶点,6个面,12条棱的图形不是长方体就是正方体。
4.一个长方体礼品盒如下图。现在用一根彩带将它捆扎起来,这根彩带至少长多少分米
(打结处长3 dm)
5.用两个完全一样的正方体拼成一个长方体,棱长之和减少了32 cm。原来一个正方体的棱长和是多少
正方体、长方体的展开图
1.把长方体纸盒沿着棱剪开,得到下面的展开图。请在图上标出下面、后面和左面。
2.把下图折叠起来,可以围成一个( )体。这时( )号和( )号相对;( )号和( )号相对;( )号和( )号相对。
3.下面的图形中,能折成正方体的有( )。
4.(易错题)判断。(对的画“√”,错的画“ × ”)
(1)6个相等的正方形不管怎样排列都能围成一个正方体。
(2)如果把一个正方体纸盒的表面完全展开,至少要剪开7条棱。
5.下面5种形状的硬纸各有若干张,选择其中的哪几种,每种选几张,正好可以围成一个长方体 ( )
A.①号2张,③号4张
B.②号2张,③号2张,①号2张
C.①号2张,③号2张,④号2张
D.①号2张,⑤号4张
6.根据下图填空。
折叠后围成的长方体的长是( )cm,宽是( )cm,高是( )cm,最大面的面积是( )cm2。
7.下面左边所示的三个正方体,( )和( )展开(数字朝外)后可以得到右边的展开图。
8.下面是一张长方形纸。试着把它剪成3块,折成3个无盖的正方体纸盒。(用笔在图中画出来)
第三课时 长方体表面积的意义及计算方法
1.填一填。
(1)长方体(或正方体)( )个面的总面积,叫作它的表面积。
(2)一个长方体纸盒(如图),做这个纸盒需要多少平方厘米的硬纸板
①上面的面积: _________ ;②前面的面积: _________ ;③左面的面积: _________ ;表面积:( _________ + _________ + _________ ) × 2 = _________
答:做这个纸盒需要 _________ cm2的硬纸板。
2.一个长方体铁皮水箱,长和宽都是7 dm,深8 dm。做这样一个水箱至少需要铁皮多少平方分米 (水箱有盖)
3.计算下面正方体的表面积。
(1)每个面的面积:
(2)正方体的表面积:
_________ × 6 = _________
4.张师傅要给一个棱长为3 dm的正方体木箱喷漆,喷漆的面积是多少平方分米
5.(易错题)填一填。
(1)一个正方体的棱长扩大到原来的3倍,它的表面积扩大到原来的( )倍。
(2)一个长方体的长、宽、高分别扩大到原来的4倍,它的表面积扩大到原来的( )倍。
6.把1个正方体木块锯成3个完全一样的长方体,表面积增加了18 cm2,原来这个正方体木块的表面积是多少平方厘米
7.如图,有两个一样的长方体饼干盒,用包装纸将它们全封闭包装在一起拼成一个新的长方体。请你设计出3种方案,写出所拼成的长方体的长、宽、高,再计算出每种方案拼成的长方体的表面积。
第四课时 长方体和正方体表面积的计算
1.填一填。
(1)一个长方体鱼缸,长8分米,宽5分米,高6分米,前面的玻璃打破了,修理时配的玻璃的面积是( )平方分米。
(2)一个长方体游泳池,长50米,宽20米,深1.5米。给这个游泳池的四壁及底面贴上瓷砖,贴瓷砖的面积是( )个面的面积和,是( )平方米。
2.生产一个如图所示的长方体手提袋(无盖),至少需要多少平方分米的材料
3.(易错题)一根长2米的通风管,横截面是周长为8分米的正方形,现要制作4根这样的通风管,至少需要铁皮多少平方分米
4.如图是牙膏盒的直观图。做这个牙膏盒至少需要多少平方厘米的硬纸板
5.一个底面是正方形的长方体铁箱,如果把它的侧面展开,正好是一个边长为40厘米的正方形。这个铁箱的表面积是多少平方厘米
6.电影院大门前有6级台阶,每级台阶长6米,宽0.3米,高0.2米。
(1)6级台阶一共占地多少平方米
(2)给这些台阶铺地毯,至少需要多少平方米的地毯
一个长方体的底面是边长为2分米的正方形,长方体的高为4分米,如果把它的高增加5厘米,它的表面积会增加多少平方厘米
答案
第1课时长方体和正方体的认识
(1)3 1
(2)面 棱 顶点 填图略
(3)6 12 8
(4)长方形 完全相同 长度相等
(5)正方形 相等 长方体
2.(1)长方 2 0.5 0.5 长方 1
正方 0.25 2 0.5 1 4 8
(2)正方 5 6
3.(1)√(2) ×
4.8 × 2 + 8 × 2 + 3 × 4 + 3 = 47(dm)答:这根彩带至少长47 dm。
5.5.32 ÷ 8 × 12 = 48(cm)
答:原来一个正方体的棱长和是48 cm。
第2课时长方体和正方体的展开图
2.正方 1 4 2 5 3 6
3.①②③⑤⑦⑧
4.(1) × (2)√
5.C
6.11 2 5 55
7.①②
8.
(答案不唯一)
第3课时长方体和正方体表面积的计算
1.(1)6
(2)①10 × 6 = 60(cm2)
②10 × 4 = 40(cm2) ③4 × 6 = 24(cm2)
60 40 24 248(cm2) 248
2.7 × 7 × 2 + 7 × 8 × 4 = 322(dm2)
答:做这样一个水箱至少需要铁皮322 dm2。
3.(1)4 × 4 = 16(dm2)
(2)16 96(dm2)
4.3 × 3 × 6 = 54(dm2)
答:喷漆的面积是54 dm2。
5.(1)9(2)16
6.18 ÷ 4 × 6 = 27(cm2)
答:原来这个正方体木块的表面积是27 cm2。
7.10 6 4 248 20 6 2 344
12 10 2 328
第4课时长方体和正方体表面积的计算
1.(1)48(2)5 1210
2.(3 × 4 + 0.8 × 4) × 2 + 3 × 0.8 = 32.8(平方分米)
答:至少需要32.8平方分米的材料。
3.8 ÷ 4 = 2(分米) 2米 = 20分米
2 × 20 × 4 × 4 = 640(平方分米)
答:至少需要铁皮640平方分米。
4.5 × 5 × 2 + 5 × 18 × 4 = 410(cm2)
答:做这个牙膏盒至少需要410 cm2的硬纸板。
5.40 ÷ 4 = 10(厘米)
40 × 10 × 4 + 10 × 10 × 2 = 1800(平方厘米)答:这个铁箱的表面积是1800平方厘米。
6.(1)6 × 0.3 × 6 = 10.8(平方米)答:6级台阶一共占地10.8平方米。
(2)(6 × 0.3 + 6 × 0.2) × 6 = 18(平方米)答:至少需要18平方米的地毯。
7.2分米 = 20厘米 7.2分米 = 20厘米20 × 5 × 4 = 400(平方厘米)
答:它的表面积会增加400平方厘米。
