2022-2023学年苏科版七年级数学上册6.3 余角、补角、对顶角1 课件(共20张PPT)
文档属性
| 名称 | 2022-2023学年苏科版七年级数学上册6.3 余角、补角、对顶角1 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 193.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-24 00:00:00 | ||
图片预览





文档简介
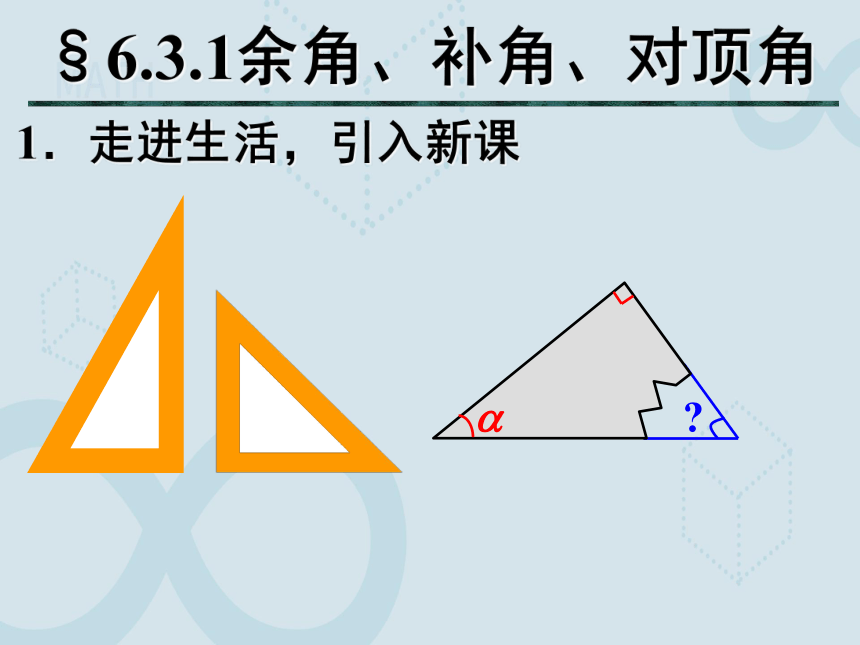
(共20张PPT)
6.3余角、补角、对顶角
1.走进生活,引入新课
§6.3.1余角、补角、对顶角
a
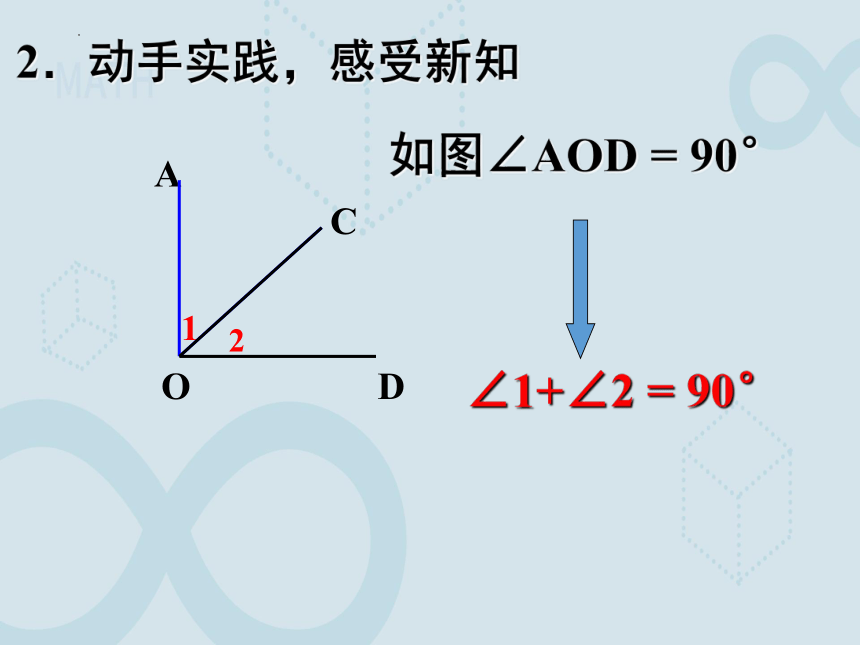
如图∠AOD = 90°
∠1+∠2 = 90°
O
A
D
C
1
2
2.动手实践,感受新知
两个角的和等于90°(直角),
就说这两个角互为余角,简称互余。
注意:和两个角的位置无关。
两个角的和等于90°(直角),
就说这两个角互为余角,简称互余。
1
2
练一练:
1、如图 ∠1+∠2=90°,
(1)∠1与∠2互为_____;
(2)∠1的余角是______;
(3)∠1是______的余角.
如果∠1+∠2=90°,那么∠1与∠2互为余角
余角
∠2
∠2
注意:
两角互余只有数量关系,
没有位置关系
互余是指两个角之间的关系
2、画出2个∠COB的余角
C
O
B
A
D
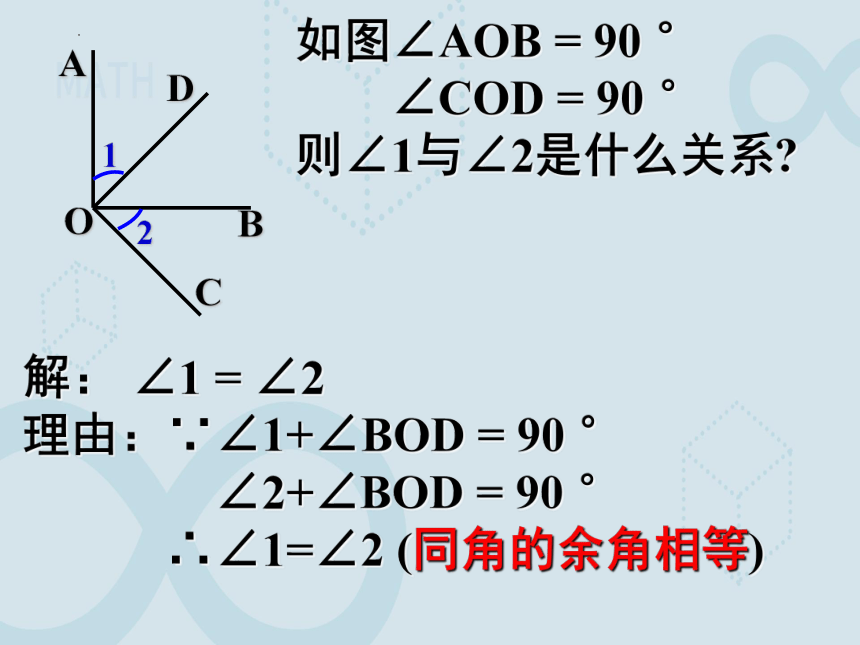
如图∠AOB = 90 °
∠COD = 90 °
则∠1与∠2是什么关系
解: ∠1 = ∠2
理由:∵∠1+∠BOD = 90 °
∠2+∠BOD = 90 °
∴∠1=∠2 (同角的余角相等)
A
O
B
C
D
1
2
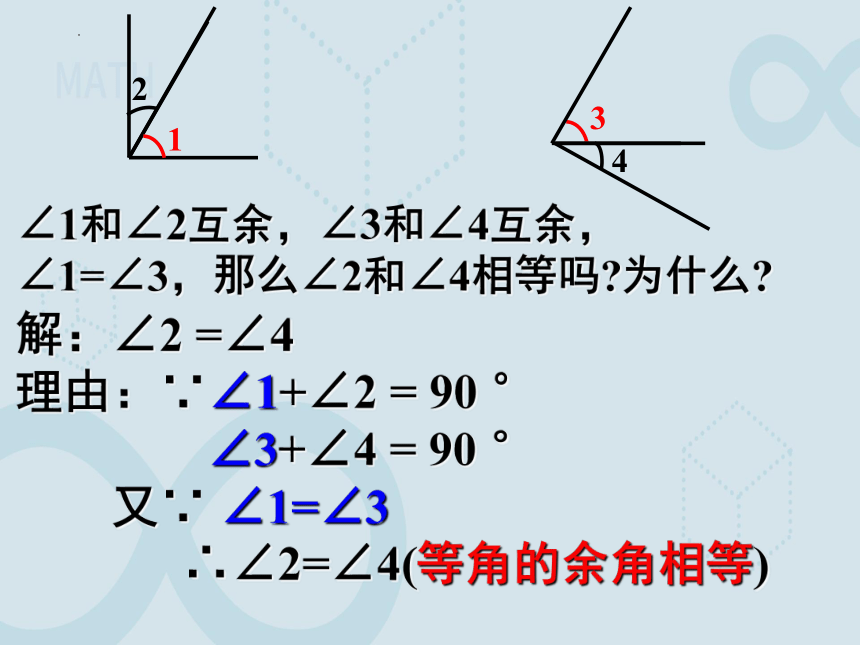
∠1和∠2互余,∠3和∠4互余,
∠1=∠3,那么∠2和∠4相等吗 为什么
1
2
3
4
解:∠2 =∠4
理由:∵∠1+∠2 = 90 °
∠3+∠4 = 90 °
又∵ ∠1=∠3
∴∠2=∠4(等角的余角相等)
两个角的和等于180°(平角),
就说这两个角互为补角,简称互补。
同角(等角)的补角相等。
注意:和两个角的位置无关。
1
2
具有如下位置的两个补角叫互为邻补角
画出∠COB的邻补角
C
O
B
D
E
如图,直线AB和CD相交于点O
我们就把其中的∠1和∠2叫做对顶角
3
4
D
B
C
O
A
那么∠3和∠4 呢?
对顶角相等
2
1
对顶角
结论:
对顶角只有在两条直线相交才会出现
找出下图中所有的对顶角
A
E
D
C
B
O
F
这里有对顶角吗
1.下列各图中,∠1与∠2是对顶角的是( )
1
2
A
1
2
B
1
2
D
自主评价,反馈调控
D
1
2
C
2.判断:
①互余的两个角必定都是锐角. ( )
②一个角的补角一定是钝角. ( )
③若∠1+∠2+∠3=90°,
那么∠1、∠2、∠3互为余角. ( )
④两个角互补,那么这两个角中,必定一个是锐角,另一个是钝角. ( )
⑤一个角的余角一定比这个角的补角小( )
⑥若 AOB与 BOC互补,则A、O、C同在一直线上. ( )
√
×
×
×
√
×
O
A
B
3.要测量两堵墙所成的角∠AOB的度数,
但人不能进入围墙,如何测量?
C
D
例1.已知:∠a =50°17′
求:∠a 的余角和补角.
一个角的余角与补角又有什么关系
练习1.已知:∠b =26°36′
求:∠b 的余角和补角.
1.如果一个角的补角是150 ° ,
那么这个角的余角是__________.
2.如果一个角的余角是19 °21 ′,
那么这个角的补角是__________.
60 °
109 °21 ′
例2.若一个角的补角等于它的余角的4倍, 求这个角的度数。
练习2.已知一个角的补角比这个角的余角的
3倍小20°,求这个角的度数.
例3.已知:如图O是直线AB上的一点,
OD、OE分别是∠AOC和∠BOC 的平分线.
(1)指出图中∠AOD的补角;∠BOC的补角
(2)写出图中所有互余的角.
(3)写出图中所有互补的角.
E
C
D
B
A
O
4对
5对
练习3.如图,AOB为一条直线,
∠1+∠2=90 ,∠COD是直角
(1)请写出图中相等的角,并说明理由;
(2)请分别写出图中互余的角和互补的角。
E
B
D
C
A
O
2
1
互为余角 互为补角
对应图形
数量关系
性 质
∠1+∠2=90°
∠1+∠2=180 °
同角或等角的
余角相等。
同角或等角的
补角相等。
1
2
1
2
课堂小结
6.3余角、补角、对顶角
1.走进生活,引入新课
§6.3.1余角、补角、对顶角
a
如图∠AOD = 90°
∠1+∠2 = 90°
O
A
D
C
1
2
2.动手实践,感受新知
两个角的和等于90°(直角),
就说这两个角互为余角,简称互余。
注意:和两个角的位置无关。
两个角的和等于90°(直角),
就说这两个角互为余角,简称互余。
1
2
练一练:
1、如图 ∠1+∠2=90°,
(1)∠1与∠2互为_____;
(2)∠1的余角是______;
(3)∠1是______的余角.
如果∠1+∠2=90°,那么∠1与∠2互为余角
余角
∠2
∠2
注意:
两角互余只有数量关系,
没有位置关系
互余是指两个角之间的关系
2、画出2个∠COB的余角
C
O
B
A
D
如图∠AOB = 90 °
∠COD = 90 °
则∠1与∠2是什么关系
解: ∠1 = ∠2
理由:∵∠1+∠BOD = 90 °
∠2+∠BOD = 90 °
∴∠1=∠2 (同角的余角相等)
A
O
B
C
D
1
2
∠1和∠2互余,∠3和∠4互余,
∠1=∠3,那么∠2和∠4相等吗 为什么
1
2
3
4
解:∠2 =∠4
理由:∵∠1+∠2 = 90 °
∠3+∠4 = 90 °
又∵ ∠1=∠3
∴∠2=∠4(等角的余角相等)
两个角的和等于180°(平角),
就说这两个角互为补角,简称互补。
同角(等角)的补角相等。
注意:和两个角的位置无关。
1
2
具有如下位置的两个补角叫互为邻补角
画出∠COB的邻补角
C
O
B
D
E
如图,直线AB和CD相交于点O
我们就把其中的∠1和∠2叫做对顶角
3
4
D
B
C
O
A
那么∠3和∠4 呢?
对顶角相等
2
1
对顶角
结论:
对顶角只有在两条直线相交才会出现
找出下图中所有的对顶角
A
E
D
C
B
O
F
这里有对顶角吗
1.下列各图中,∠1与∠2是对顶角的是( )
1
2
A
1
2
B
1
2
D
自主评价,反馈调控
D
1
2
C
2.判断:
①互余的两个角必定都是锐角. ( )
②一个角的补角一定是钝角. ( )
③若∠1+∠2+∠3=90°,
那么∠1、∠2、∠3互为余角. ( )
④两个角互补,那么这两个角中,必定一个是锐角,另一个是钝角. ( )
⑤一个角的余角一定比这个角的补角小( )
⑥若 AOB与 BOC互补,则A、O、C同在一直线上. ( )
√
×
×
×
√
×
O
A
B
3.要测量两堵墙所成的角∠AOB的度数,
但人不能进入围墙,如何测量?
C
D
例1.已知:∠a =50°17′
求:∠a 的余角和补角.
一个角的余角与补角又有什么关系
练习1.已知:∠b =26°36′
求:∠b 的余角和补角.
1.如果一个角的补角是150 ° ,
那么这个角的余角是__________.
2.如果一个角的余角是19 °21 ′,
那么这个角的补角是__________.
60 °
109 °21 ′
例2.若一个角的补角等于它的余角的4倍, 求这个角的度数。
练习2.已知一个角的补角比这个角的余角的
3倍小20°,求这个角的度数.
例3.已知:如图O是直线AB上的一点,
OD、OE分别是∠AOC和∠BOC 的平分线.
(1)指出图中∠AOD的补角;∠BOC的补角
(2)写出图中所有互余的角.
(3)写出图中所有互补的角.
E
C
D
B
A
O
4对
5对
练习3.如图,AOB为一条直线,
∠1+∠2=90 ,∠COD是直角
(1)请写出图中相等的角,并说明理由;
(2)请分别写出图中互余的角和互补的角。
E
B
D
C
A
O
2
1
互为余角 互为补角
对应图形
数量关系
性 质
∠1+∠2=90°
∠1+∠2=180 °
同角或等角的
余角相等。
同角或等角的
补角相等。
1
2
1
2
课堂小结
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
