鲁教版(五四学制)七年级上册1.3探索三角形全等的条件(第二课时)课件(共22张PPT)
文档属性
| 名称 | 鲁教版(五四学制)七年级上册1.3探索三角形全等的条件(第二课时)课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 703.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-24 00:00:00 | ||
图片预览


文档简介
(共22张PPT)
昨天,王老师不小心将一块三角形教具打碎为两块,而他只想带其中的一块碎片到商店去,配一块与原来一样的三角形教具。你能告诉王老师带哪块去合适吗?为什么?
问题情境
回顾思考
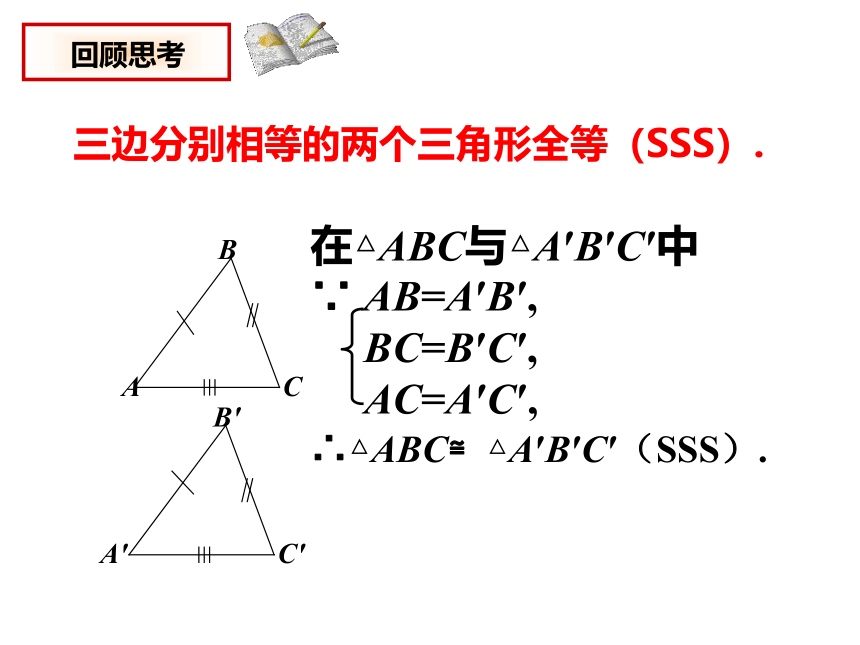
三边分别相等的两个三角形全等(SSS).
A
B
C
A′
B′
C′
在△ABC与△A′B′C′中
∵ AB=A′B′,
BC=B′C′,
AC=A′C′,
∴△ABC≌△A′B′C′(SSS).
继续探讨三角形全等的条件:
两角一边
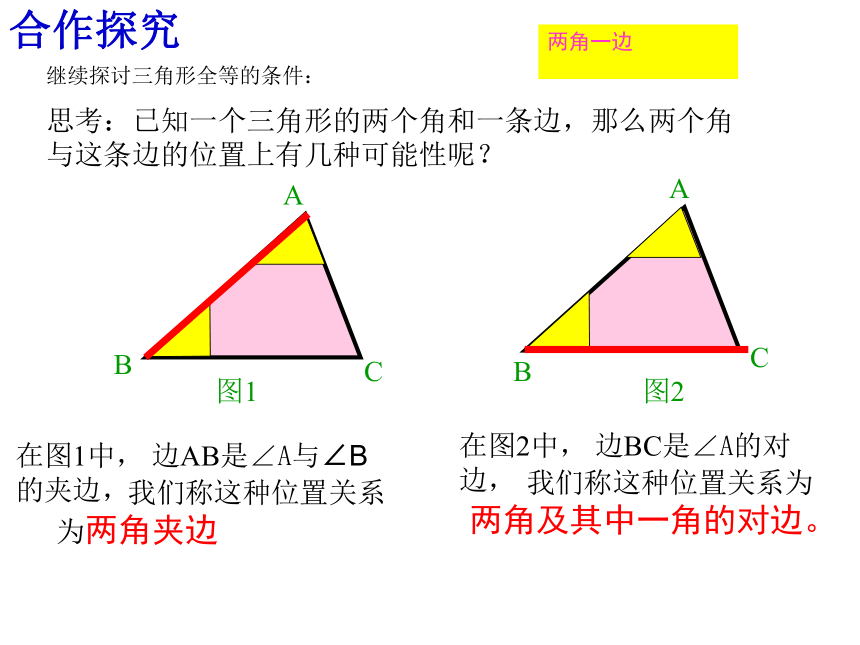
思考:已知一个三角形的两个角和一条边,那么两个角
与这条边的位置上有几种可能性呢?
A
B
C
A
B
C
图1
图2
在图1中, 边AB是∠A与∠B的夹边,
在图2中, 边BC是∠A的对边,
我们称这种位置关系为两角夹边
我们称这种位置关系为两角及其中一角的对边。
合作探究
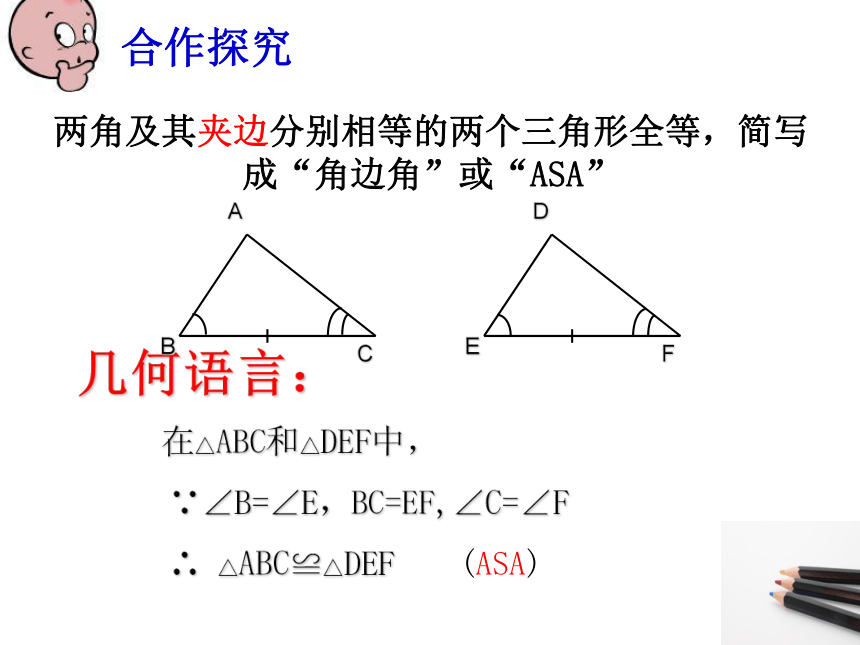
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”
几何语言:
在△ABC和△DEF中,
∵∠B=∠E,BC=EF,∠C=∠F
∴ △ABC≌△DEF
(ASA)
D
E
F
C
A
B
合作探究
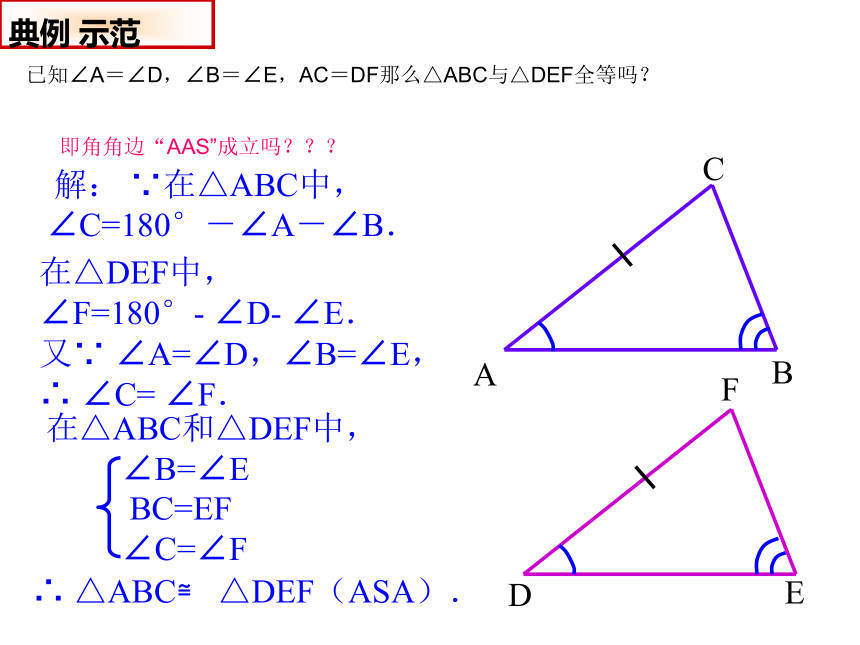
解: ∵在△ABC中,
∠C=180°-∠A-∠B.
A
B
D
E
C
F
已知∠A=∠D,∠B=∠E,AC=DF那么△ABC与△DEF全等吗?
即角角边“AAS”成立吗???
又∵ ∠A=∠D,∠B=∠E,
∴ ∠C= ∠F.
在△DEF中,
∠F=180°- ∠D- ∠E.
∴ △ABC≌ △DEF(ASA).
在△ABC和△DEF中,
∠B=∠E
BC=EF
∠C=∠F
典例 示范
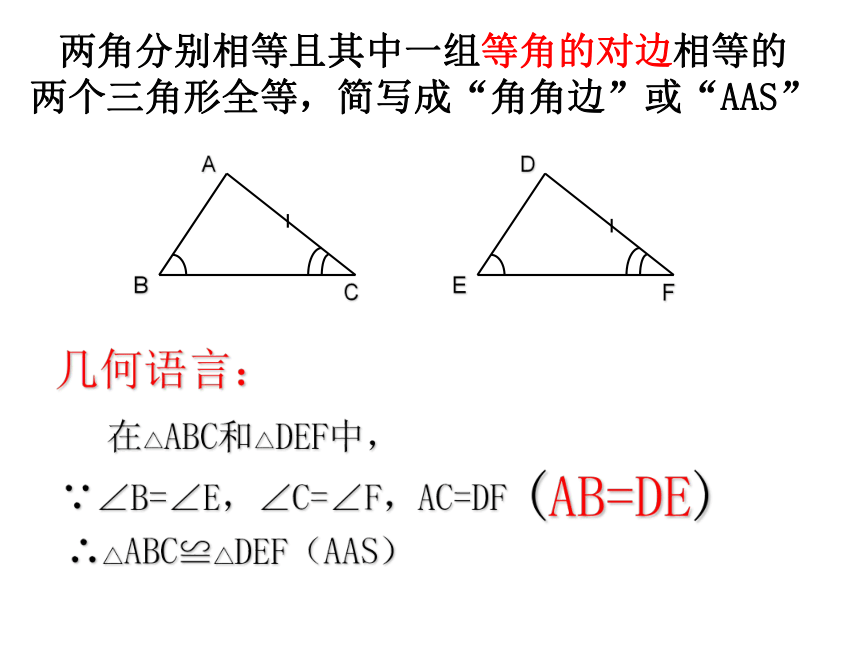
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成“角角边”或“AAS”
几何语言:
在△ABC和△DEF中,
∵∠B=∠E,∠C=∠F,AC=DF
∴△ABC≌△DEF(AAS)
(AB=DE)
A
B
C
D
E
F
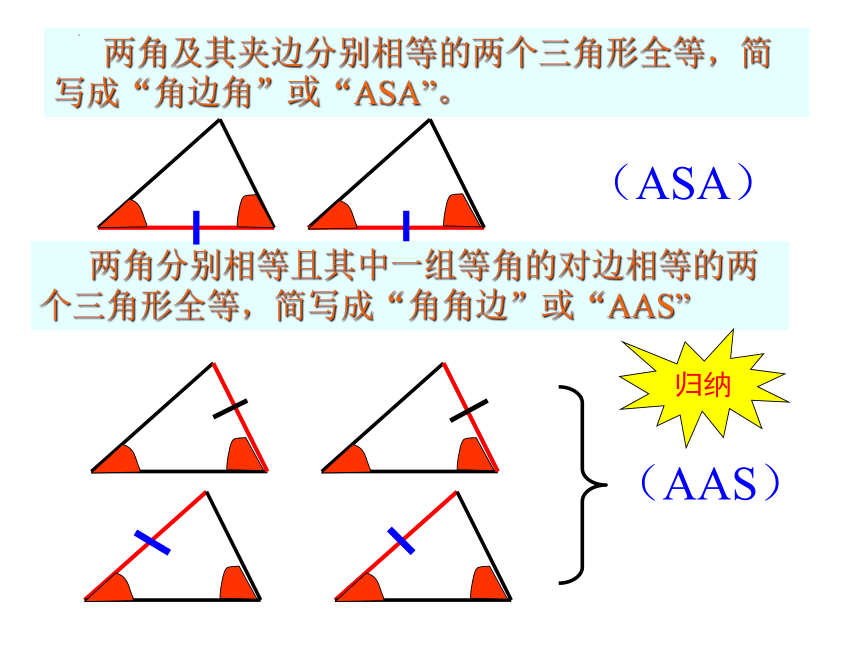
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”。
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成“角角边”或“AAS”
(ASA)
(AAS)
归纳
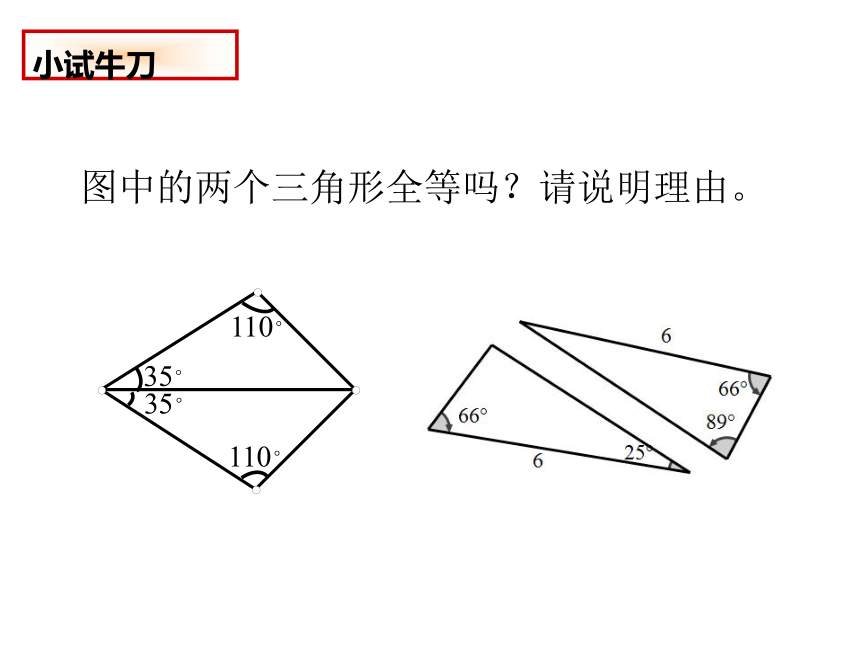
图中的两个三角形全等吗?请说明理由。
35°
35°
110°
110°
小试牛刀
4. 如图,O是AB的中点, ∠A=∠B ,
△AOC 与 △BOD 全等吗 为什么?
在△AOC与△BOD中
∠A=∠B (已知)
AO=BO
∠AOC= ∠BOD (对顶角相等)
∴ △ABE ≌△ACD (ASA)
解:∵ O是AB的中点(已知),
∴ AO=BO(中点的定义)
典例 示范
如图,AB⊥BC,AD⊥DC,∠1=∠2,
那么△ABC和△ADC全等吗?
解:∵AB⊥BC,AD⊥DC(已知)
A
B
C
D
(
(
1 2
∴ ∠B=∠D=90°(垂直的定义)
在 △ABC和△ADC中
AC=AC(公共边)
∠1=∠2 (已知)
∠B=∠D
∴ △ABC≌△ADC(AAS)
小试牛刀
如图 ,AB=AC,∠B=∠C,那么△ABE和△ACD全等吗?为什么?
A
E
D
C
B
解:全等
在△ABE与△ACD中
∠B=∠C
AB=AC
∴ △ABE ≌△ACD
∠A= ∠A
(公共角)
(ASA)
( 已知)
(已知)
小试牛刀
如图 ,AD=AE,∠B=∠C,那么△ABE和△ACD全等吗?为什么?
A
E
D
C
B
解:全等
在△ABE与△ACD中
∠B=∠C (已知)
∠A= ∠A (公共角)
AD=AE (已知)
∴ △ABE ≌△ACD (AAS)
典例 示范
2.如图,AD=AE,∠B=∠C,那么BE和CD相等么?为什么?
∴ BE=CD (全等三角形对应边相等)
A
E
D
C
B
在△ABE与△ACD中
∠B=∠C (已知)
∠A= ∠A (公共角)
AD=AE (已知)
∴ △ABE ≌△ACD (AAS)
拓展应用
解:
BE=CD
昨天,王老师不小心将一块三角形教具打碎为两块,而他只想带其中的一块碎片到商店去,配一块与原来一样的三角形教具。你能告诉王老师带哪块去合适吗?为什么?
问题情境
规律总结
寻找三角形全等的条件
1.直接条件:
2.隐含条件:
3.间接条件:
即已知中直接给出的三角形的对应边或
对应角的条件。
如公共边、公共角、对顶角等。
即已知中所给条件不是三角形的对应边或
对应角,需要进一步推理。
小结
知识要点:
(1)两角及其夹边对应相等的两个三角形全等。简写成“角边角”或“ASA”。
(2)两角分别相等且其中一组等角的对边相等的两个三角形全等。简写成“角角边”或“AAS”。
(3)运用ASA,AAS证明线段相等﹑角相等。
数学思想:
本节课要学会用分类的思想﹑转化的思想解决问题。
A
B
C
D
E
F
1、如图∠ACB=∠DFE,BC=EF,那么应补充一个条件 ------------------------- ,才能使△ABC≌△DEF (写出一个即可)。
∠B=∠E
或∠A=∠D
当堂检测
(ASA)
(AAS)
AB∥DE
2.已知:如图,M是线段AB的中点,∠C=∠D,∠1=∠2。
求证:△AMC≌△BMD。
A
B
C
D
M
1
2
当堂检测
选做题.
如图,已知 AB=AD, ∠C=∠E,∠1=∠2,△ABC和△ADE全等吗?为什么?
C
E
A
B
D
2
1
当堂检测
作业
一、必做
完成习题1.8 1、2题
二、选做
完成3题
教师寄语:
全等三角形是三角形之间最简单的
关系,但它却是证明线段相等和角相等的重要方法,虽然简单却不平凡。愿同学们能象它一样,用最简单的梦想造就最不平凡的人生!
昨天,王老师不小心将一块三角形教具打碎为两块,而他只想带其中的一块碎片到商店去,配一块与原来一样的三角形教具。你能告诉王老师带哪块去合适吗?为什么?
问题情境
回顾思考
三边分别相等的两个三角形全等(SSS).
A
B
C
A′
B′
C′
在△ABC与△A′B′C′中
∵ AB=A′B′,
BC=B′C′,
AC=A′C′,
∴△ABC≌△A′B′C′(SSS).
继续探讨三角形全等的条件:
两角一边
思考:已知一个三角形的两个角和一条边,那么两个角
与这条边的位置上有几种可能性呢?
A
B
C
A
B
C
图1
图2
在图1中, 边AB是∠A与∠B的夹边,
在图2中, 边BC是∠A的对边,
我们称这种位置关系为两角夹边
我们称这种位置关系为两角及其中一角的对边。
合作探究
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”
几何语言:
在△ABC和△DEF中,
∵∠B=∠E,BC=EF,∠C=∠F
∴ △ABC≌△DEF
(ASA)
D
E
F
C
A
B
合作探究
解: ∵在△ABC中,
∠C=180°-∠A-∠B.
A
B
D
E
C
F
已知∠A=∠D,∠B=∠E,AC=DF那么△ABC与△DEF全等吗?
即角角边“AAS”成立吗???
又∵ ∠A=∠D,∠B=∠E,
∴ ∠C= ∠F.
在△DEF中,
∠F=180°- ∠D- ∠E.
∴ △ABC≌ △DEF(ASA).
在△ABC和△DEF中,
∠B=∠E
BC=EF
∠C=∠F
典例 示范
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成“角角边”或“AAS”
几何语言:
在△ABC和△DEF中,
∵∠B=∠E,∠C=∠F,AC=DF
∴△ABC≌△DEF(AAS)
(AB=DE)
A
B
C
D
E
F
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”。
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成“角角边”或“AAS”
(ASA)
(AAS)
归纳
图中的两个三角形全等吗?请说明理由。
35°
35°
110°
110°
小试牛刀
4. 如图,O是AB的中点, ∠A=∠B ,
△AOC 与 △BOD 全等吗 为什么?
在△AOC与△BOD中
∠A=∠B (已知)
AO=BO
∠AOC= ∠BOD (对顶角相等)
∴ △ABE ≌△ACD (ASA)
解:∵ O是AB的中点(已知),
∴ AO=BO(中点的定义)
典例 示范
如图,AB⊥BC,AD⊥DC,∠1=∠2,
那么△ABC和△ADC全等吗?
解:∵AB⊥BC,AD⊥DC(已知)
A
B
C
D
(
(
1 2
∴ ∠B=∠D=90°(垂直的定义)
在 △ABC和△ADC中
AC=AC(公共边)
∠1=∠2 (已知)
∠B=∠D
∴ △ABC≌△ADC(AAS)
小试牛刀
如图 ,AB=AC,∠B=∠C,那么△ABE和△ACD全等吗?为什么?
A
E
D
C
B
解:全等
在△ABE与△ACD中
∠B=∠C
AB=AC
∴ △ABE ≌△ACD
∠A= ∠A
(公共角)
(ASA)
( 已知)
(已知)
小试牛刀
如图 ,AD=AE,∠B=∠C,那么△ABE和△ACD全等吗?为什么?
A
E
D
C
B
解:全等
在△ABE与△ACD中
∠B=∠C (已知)
∠A= ∠A (公共角)
AD=AE (已知)
∴ △ABE ≌△ACD (AAS)
典例 示范
2.如图,AD=AE,∠B=∠C,那么BE和CD相等么?为什么?
∴ BE=CD (全等三角形对应边相等)
A
E
D
C
B
在△ABE与△ACD中
∠B=∠C (已知)
∠A= ∠A (公共角)
AD=AE (已知)
∴ △ABE ≌△ACD (AAS)
拓展应用
解:
BE=CD
昨天,王老师不小心将一块三角形教具打碎为两块,而他只想带其中的一块碎片到商店去,配一块与原来一样的三角形教具。你能告诉王老师带哪块去合适吗?为什么?
问题情境
规律总结
寻找三角形全等的条件
1.直接条件:
2.隐含条件:
3.间接条件:
即已知中直接给出的三角形的对应边或
对应角的条件。
如公共边、公共角、对顶角等。
即已知中所给条件不是三角形的对应边或
对应角,需要进一步推理。
小结
知识要点:
(1)两角及其夹边对应相等的两个三角形全等。简写成“角边角”或“ASA”。
(2)两角分别相等且其中一组等角的对边相等的两个三角形全等。简写成“角角边”或“AAS”。
(3)运用ASA,AAS证明线段相等﹑角相等。
数学思想:
本节课要学会用分类的思想﹑转化的思想解决问题。
A
B
C
D
E
F
1、如图∠ACB=∠DFE,BC=EF,那么应补充一个条件 ------------------------- ,才能使△ABC≌△DEF (写出一个即可)。
∠B=∠E
或∠A=∠D
当堂检测
(ASA)
(AAS)
AB∥DE
2.已知:如图,M是线段AB的中点,∠C=∠D,∠1=∠2。
求证:△AMC≌△BMD。
A
B
C
D
M
1
2
当堂检测
选做题.
如图,已知 AB=AD, ∠C=∠E,∠1=∠2,△ABC和△ADE全等吗?为什么?
C
E
A
B
D
2
1
当堂检测
作业
一、必做
完成习题1.8 1、2题
二、选做
完成3题
教师寄语:
全等三角形是三角形之间最简单的
关系,但它却是证明线段相等和角相等的重要方法,虽然简单却不平凡。愿同学们能象它一样,用最简单的梦想造就最不平凡的人生!
