鲁教版(五四制)九年级上册2.5 三角函数的应用(第一课时)课件(共25张PPT)
文档属性
| 名称 | 鲁教版(五四制)九年级上册2.5 三角函数的应用(第一课时)课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 9.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-24 21:23:07 | ||
图片预览







文档简介
(共25张PPT)
三角函数的应用(一)
第二章直角三角形的边角关系
5
学习目标
回顾与思考
探究新知
知识总结
巩固提升
01
回顾与思考
壹
MY RESUME
回顾与思考
B
C
a
b
A
c
如图,已知直角三角形ABC,你能想到哪些知识,请思考后在你的学案上完成,2分钟后我们交流
特殊角300,450,600角的三角函数值.
回顾与思考
直角三角形的边角关系:
B
C
a
b
A
c
两锐角之间的关系:
∠A+ ∠ B=90°
三边之间的关系:
a2+b2=c2
角与边之间的关系:
02
探究新知
贰
MY RESUME
01
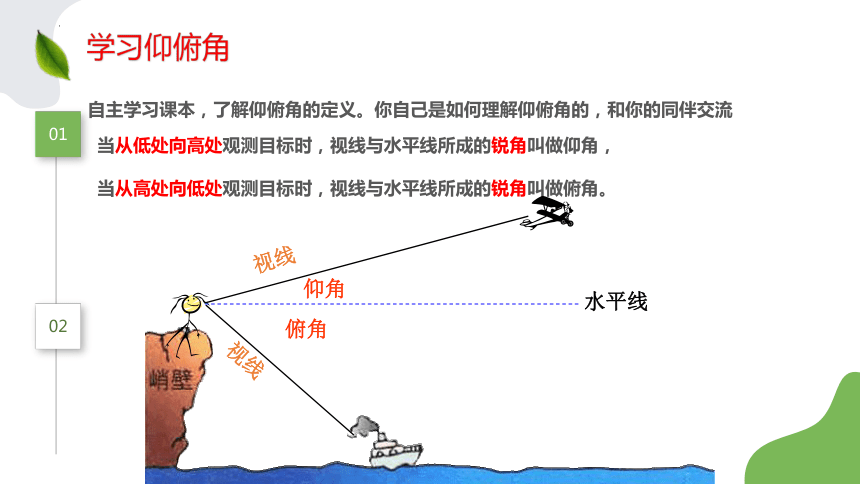
自主学习课本,了解仰俯角的定义。你自己是如何理解仰俯角的,和你的同伴交流
02
学习仰俯角
当从低处向高处观测目标时,视线与水平线所成的锐角叫做仰角,
当从高处向低处观测目标时,视线与水平线所成的锐角叫做俯角。
俯角
仰角
水平线
视线
视线
03
04
由A测得B的俯角
由B测得A的仰角
水平线
水平线
B
A
仰角与俯角的相互转化
运用仰俯角解决问题
58.6°
200 m
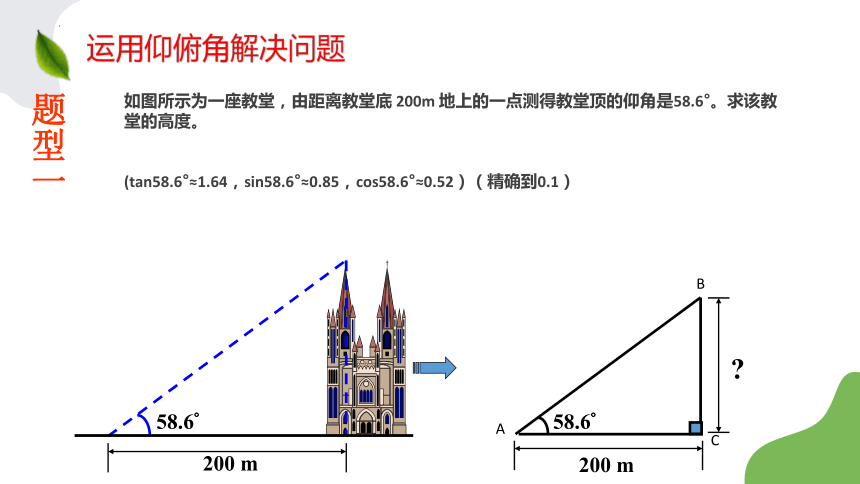
如图所示为一座教堂,由距离教堂底 200m 地上的一点测得教堂顶的仰角是58.6°。求该教堂的高度。
(tan58.6°≈1.64,sin58.6°≈0.85,cos58.6°≈0.52)(精确到0.1)
58.6°
200 m
题型一
A
B
C
运用仰俯角解决问题
58.6°
200 m
如图所示为一座教堂,由距离教堂底 200m 地上的一点测得教堂顶的仰角是58.6°。求该教堂的高度。
(tan58.6°≈1.64,sin58.6°≈0.85,cos58.6°≈0.52)(精确到0.1)
58.6°
200 m
题型一
A
B
C
若教堂上方有一避雷针,测得避雷针的顶部的仰角为60°,求避雷针的高度。
60°
2
3
4
1
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至B处,测得仰角为60°,小明的身高为1.5 m,那么该塔有多高 (结果精确到0.1 m)
独立完成题目
小组交流做法
展示小组做法
总结题目做法
题型二
运用仰俯角解决问题
2
3
4
1
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至B处,测得仰角为60°,小明的身高为1.5 m,那么该塔有多高 (结果精确到0.1 m)
独立完成题目
小组交流做法
展示小组做法
总结题目做法
题型二
运用仰俯角解决问题
45°
45°
抽象出三角形问题
1
分析问题
2
构造直角三角形解直角三角形
3
得到实际问题答案
4
解决问题方法
Fresh resume job report self introduction
方向角问题
你还记得方向角是怎么描述的吗?
新TOFEL考试120分
方向角问题
方向角【direction angle】指的是采用某坐标轴方向作为标准方向所确定的方位角。方向角是从正北或正南方向到目标方向所形成的锐角。
新TOFEL考试120分
利用方向角解决问题
如图,海中有一个小岛A,该岛四周10 n mile内有暗礁.今有货船由西向东航行,开始在A岛南偏西55°的B处,往东行驶20 n mile后到达该岛的南偏西25°的C处之后,货船继续向东航行.
你认为货轮继续向东航行途中会有触礁的危险吗 你是怎样想的 与同伴进行交流.
题型三
(sin55°≈0.82,cos55°≈0.57,tan≈1.43,sin25°≈0.42,cos25°≈0.91,tan≈0.47)
新TOFEL考试120分
自主探究二
如图,海中有一个小岛A,该岛四周10 n mile内有暗礁.今有货船由西向东航行,开始在A岛南偏西55°的B处,往东行驶20 n mile后到达该岛的南偏西25°的C处之后,货船继续向东航行.
你认为货轮继续向东航行途中会有触礁的危险吗 你是怎样想的 与同伴进行交流.
A
B
C
D
北
东
要解决这个问
题,我们可以将其数学化,如图:
题型三
(sin55°≈0.82,cos55°≈0.57,tan≈1.43,sin25°≈0.42,cos25°≈0.91,tan≈0.47)
某商场准备改善原有楼梯的安全性能,把倾角由原来的40°减至35°,已知原楼梯的长度为4m,调整后的楼梯会加长多少 楼梯多占多长一段地面 (结果精确到0.01m).
利用倾斜角解决问题
楼梯加长了多少
2
3
4
1
独立完成题目
小组交流做法
展示小组做法
总结题目做法
题型四
03
知识总结
叁
MY RESUME
抽象出三角形
解直角三角形
收获
得出实际问题答案
合作探究
问题转化
合理选择
谈谈你的收获
知识技能
思想方法
04
学以致用
肆
MY RESUME
学以致用
1.如图,物华大厦离小伟家60m,小伟从自家的窗中眺望大厦,并测得大厦顶部的仰角是45°,而大厦底部的俯角是37°,求该大厦的高度(结果精确到0.1 m) (sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,)
学以致用
2.如图,一艘船以每小时32 n mile的速度向正北航行.在A处观测到灯塔C在船的北偏东20°方向上:半小时后船航行到B处,在B处观测到灯塔C在船的北偏东65°方向上.求灯塔C与B处之间的距离(结 果精确到0.1 n mile)
在这里我很荣幸赶上了公司改革的机遇,面对了一个崭新挑战自我的时机。感谢公司领导为我们创造了这次公平竞争的机会。我非常自豪地看到我们公司改革前进的步伐,以这种公平、公正、公开的方式选拔优秀的企业人才。
公司领导为我们创造了这次公平竞争的机会。在这里我很荣幸赶上了公司改革的机遇,面对了一个崭新挑战自我的时机
个人简述
PERSONAL BRIEF
2020年,让我们撸起袖子加油干!
1、如图所示,一艘船由A港沿北偏东65°方向航行30√2 km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,求A,C两港之间的距离。
2、某校数学兴趣小组借助无人机测量一条河流的宽度CD.如图所示,一架水平飞行的无人机在A处测得正前方河流的左岸C处的俯角为α,无人机沿水平线AF方向继续飞行50 m至B处,测得正前方河流右岸D处的俯角为30°.线段AM的长为无人机距地面的铅直高度,点M,C,D在同一条直线上.其中tan α=2,MC= 50√3m.
(1)求无人机的飞行高度AM;(结果保留根号)
(2)求河流的宽度CD.(结果精确到1 m,参考数据:√2≈1.41,√3≈1.73)
拓展提高
第一步
第二步
第三步
第四步
您的内容打在这里,或者通过复制您的文本在此框中选择粘贴并选择只保留文字您的您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴并选择只保此您的内框中选择粘贴并选择只保留
或者通过复制您的文本后,在此框中选择粘贴并选择只保此您的内框中选择粘贴
添加您的标题
加强管理
技能学习
团队交流
营销培训
完成步骤
Fresh resume job report self introduction
谢谢观看
三角函数的应用(一)
第二章直角三角形的边角关系
5
学习目标
回顾与思考
探究新知
知识总结
巩固提升
01
回顾与思考
壹
MY RESUME
回顾与思考
B
C
a
b
A
c
如图,已知直角三角形ABC,你能想到哪些知识,请思考后在你的学案上完成,2分钟后我们交流
特殊角300,450,600角的三角函数值.
回顾与思考
直角三角形的边角关系:
B
C
a
b
A
c
两锐角之间的关系:
∠A+ ∠ B=90°
三边之间的关系:
a2+b2=c2
角与边之间的关系:
02
探究新知
贰
MY RESUME
01
自主学习课本,了解仰俯角的定义。你自己是如何理解仰俯角的,和你的同伴交流
02
学习仰俯角
当从低处向高处观测目标时,视线与水平线所成的锐角叫做仰角,
当从高处向低处观测目标时,视线与水平线所成的锐角叫做俯角。
俯角
仰角
水平线
视线
视线
03
04
由A测得B的俯角
由B测得A的仰角
水平线
水平线
B
A
仰角与俯角的相互转化
运用仰俯角解决问题
58.6°
200 m
如图所示为一座教堂,由距离教堂底 200m 地上的一点测得教堂顶的仰角是58.6°。求该教堂的高度。
(tan58.6°≈1.64,sin58.6°≈0.85,cos58.6°≈0.52)(精确到0.1)
58.6°
200 m
题型一
A
B
C
运用仰俯角解决问题
58.6°
200 m
如图所示为一座教堂,由距离教堂底 200m 地上的一点测得教堂顶的仰角是58.6°。求该教堂的高度。
(tan58.6°≈1.64,sin58.6°≈0.85,cos58.6°≈0.52)(精确到0.1)
58.6°
200 m
题型一
A
B
C
若教堂上方有一避雷针,测得避雷针的顶部的仰角为60°,求避雷针的高度。
60°
2
3
4
1
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至B处,测得仰角为60°,小明的身高为1.5 m,那么该塔有多高 (结果精确到0.1 m)
独立完成题目
小组交流做法
展示小组做法
总结题目做法
题型二
运用仰俯角解决问题
2
3
4
1
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至B处,测得仰角为60°,小明的身高为1.5 m,那么该塔有多高 (结果精确到0.1 m)
独立完成题目
小组交流做法
展示小组做法
总结题目做法
题型二
运用仰俯角解决问题
45°
45°
抽象出三角形问题
1
分析问题
2
构造直角三角形解直角三角形
3
得到实际问题答案
4
解决问题方法
Fresh resume job report self introduction
方向角问题
你还记得方向角是怎么描述的吗?
新TOFEL考试120分
方向角问题
方向角【direction angle】指的是采用某坐标轴方向作为标准方向所确定的方位角。方向角是从正北或正南方向到目标方向所形成的锐角。
新TOFEL考试120分
利用方向角解决问题
如图,海中有一个小岛A,该岛四周10 n mile内有暗礁.今有货船由西向东航行,开始在A岛南偏西55°的B处,往东行驶20 n mile后到达该岛的南偏西25°的C处之后,货船继续向东航行.
你认为货轮继续向东航行途中会有触礁的危险吗 你是怎样想的 与同伴进行交流.
题型三
(sin55°≈0.82,cos55°≈0.57,tan≈1.43,sin25°≈0.42,cos25°≈0.91,tan≈0.47)
新TOFEL考试120分
自主探究二
如图,海中有一个小岛A,该岛四周10 n mile内有暗礁.今有货船由西向东航行,开始在A岛南偏西55°的B处,往东行驶20 n mile后到达该岛的南偏西25°的C处之后,货船继续向东航行.
你认为货轮继续向东航行途中会有触礁的危险吗 你是怎样想的 与同伴进行交流.
A
B
C
D
北
东
要解决这个问
题,我们可以将其数学化,如图:
题型三
(sin55°≈0.82,cos55°≈0.57,tan≈1.43,sin25°≈0.42,cos25°≈0.91,tan≈0.47)
某商场准备改善原有楼梯的安全性能,把倾角由原来的40°减至35°,已知原楼梯的长度为4m,调整后的楼梯会加长多少 楼梯多占多长一段地面 (结果精确到0.01m).
利用倾斜角解决问题
楼梯加长了多少
2
3
4
1
独立完成题目
小组交流做法
展示小组做法
总结题目做法
题型四
03
知识总结
叁
MY RESUME
抽象出三角形
解直角三角形
收获
得出实际问题答案
合作探究
问题转化
合理选择
谈谈你的收获
知识技能
思想方法
04
学以致用
肆
MY RESUME
学以致用
1.如图,物华大厦离小伟家60m,小伟从自家的窗中眺望大厦,并测得大厦顶部的仰角是45°,而大厦底部的俯角是37°,求该大厦的高度(结果精确到0.1 m) (sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,)
学以致用
2.如图,一艘船以每小时32 n mile的速度向正北航行.在A处观测到灯塔C在船的北偏东20°方向上:半小时后船航行到B处,在B处观测到灯塔C在船的北偏东65°方向上.求灯塔C与B处之间的距离(结 果精确到0.1 n mile)
在这里我很荣幸赶上了公司改革的机遇,面对了一个崭新挑战自我的时机。感谢公司领导为我们创造了这次公平竞争的机会。我非常自豪地看到我们公司改革前进的步伐,以这种公平、公正、公开的方式选拔优秀的企业人才。
公司领导为我们创造了这次公平竞争的机会。在这里我很荣幸赶上了公司改革的机遇,面对了一个崭新挑战自我的时机
个人简述
PERSONAL BRIEF
2020年,让我们撸起袖子加油干!
1、如图所示,一艘船由A港沿北偏东65°方向航行30√2 km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,求A,C两港之间的距离。
2、某校数学兴趣小组借助无人机测量一条河流的宽度CD.如图所示,一架水平飞行的无人机在A处测得正前方河流的左岸C处的俯角为α,无人机沿水平线AF方向继续飞行50 m至B处,测得正前方河流右岸D处的俯角为30°.线段AM的长为无人机距地面的铅直高度,点M,C,D在同一条直线上.其中tan α=2,MC= 50√3m.
(1)求无人机的飞行高度AM;(结果保留根号)
(2)求河流的宽度CD.(结果精确到1 m,参考数据:√2≈1.41,√3≈1.73)
拓展提高
第一步
第二步
第三步
第四步
您的内容打在这里,或者通过复制您的文本在此框中选择粘贴并选择只保留文字您的您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴并选择只保此您的内框中选择粘贴并选择只保留
或者通过复制您的文本后,在此框中选择粘贴并选择只保此您的内框中选择粘贴
添加您的标题
加强管理
技能学习
团队交流
营销培训
完成步骤
Fresh resume job report self introduction
谢谢观看
