2022—2023学年鲁教版(五四制)数学八年级上册5.1平行四边形的性质第一课时 教学课件(共30张PPT)
文档属性
| 名称 | 2022—2023学年鲁教版(五四制)数学八年级上册5.1平行四边形的性质第一课时 教学课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-24 00:00:00 | ||
图片预览









文档简介
(共30张PPT)
5.1平行四边形的性质
鲁教版八年级上册第五章第一节
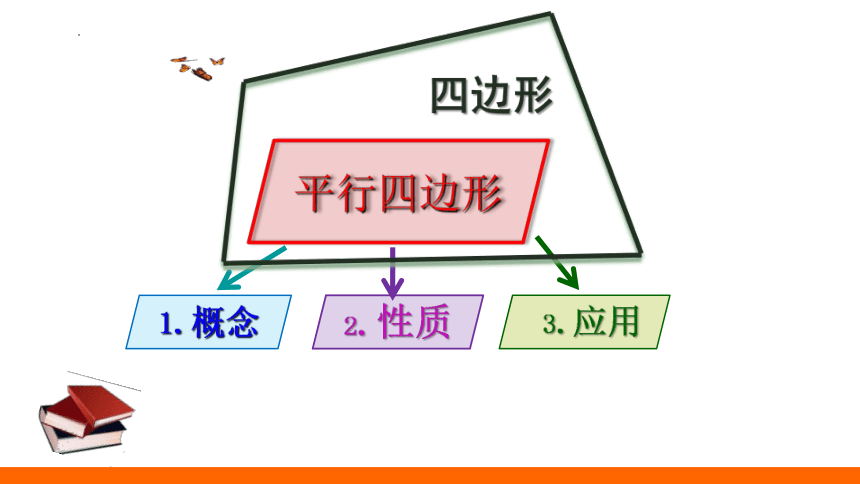
平行四边形
四边形
3.应用
1.概念
2.性质
学习目标
1. 理解并掌握平行四边形的定义及有关概念。
2. 经历探究的过程,理解与掌握平行四边形的性质及应用。
3.通过图形的变换探索平行四边形的性质及平行四边形的性质的应用。
有一块形状如图 所示的玻璃,小明不小心把EDF部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,聪明的你能根据测得的数据帮小明计算出DE的长度和∠D的度数吗?
巩固练习
创设情景,引入新知
情景导入
活动1 生活中的平行四边形
情景导入
活动1 生活中的平行四边形
探究新知
学
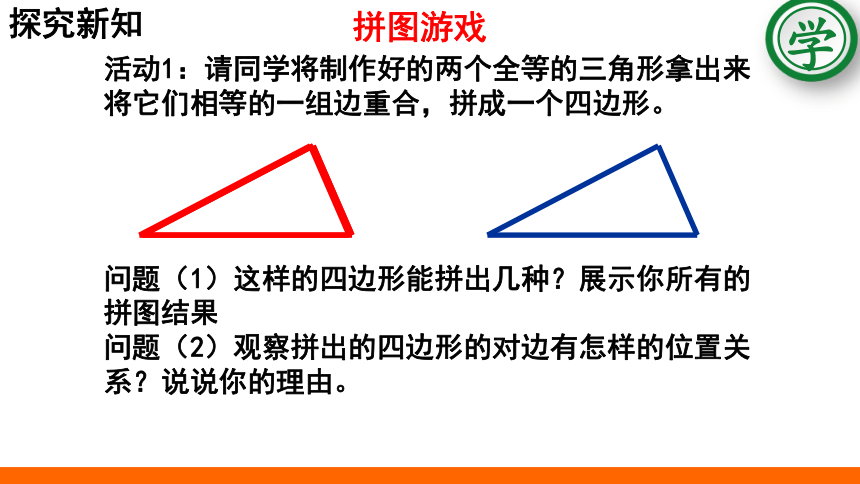
活动1:请同学将制作好的两个全等的三角形拿出来将它们相等的一组边重合,拼成一个四边形。
问题(1)这样的四边形能拼出几种?展示你所有的拼图结果
问题(2)观察拼出的四边形的对边有怎样的位置关系?说说你的理由。
拼图游戏
探究新知
展
活动2 成果展示
探究新知
学
平行四边形
从拼图可以得到什么启示?
小结:平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连接对角线转化为两个全等的三角形进行解题。
探究新知
学
平行四边形相关定义:
1、两组对边分别平行的四边形叫平行四边形。如图:四边形ABCD 是平行四边形,
记做□ ABCD ,读作平行四边形ABCD。
注意:平行四边形的表示要按一定的方向依次表示各顶点,不能有跳跃
D
A
B
C
2、平行四边形不相邻的两个顶点连成的线段叫对角线。
3、平行四边形相对的边称为 对边
相对的角称为 对角
火眼金睛
练
你能从以下图形中找出平行四边形吗?
1
2
3
4
5
两组对边分别平行,是平行四边形的一个主要特征。
探究新知
学
D
A
B
C
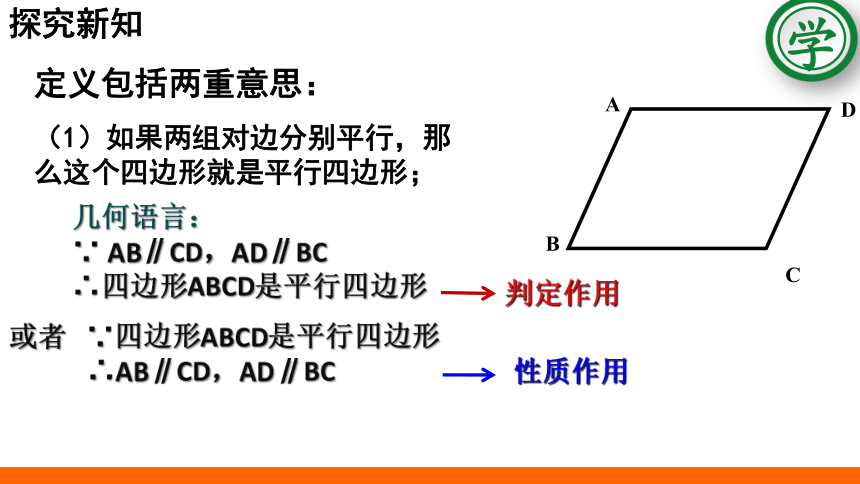
定义包括两重意思:
(1)如果两组对边分别平行,那么这个四边形就是平行四边形;
几何语言:
∵ AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
判定作用
或者 ∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
性质作用
合作探究
展
研
思考:问题(1)平行四边形是中心对称图形吗?
如果是,你能找到它的对称中心吗?
问题(2)平行四边形的对边有什么性质?
问题(3)平行四边形的对角有什么性质?
问题(4)平行四边形中相邻的两角有什么关系呢?
1、活动要求:采用度量、平移、旋转的方法探究平行四边形的性质。
2、学生利用学具(全等的三角形纸板、平行四边形纸板各一对,格尺、量角器,图钉)小组合作探究
●
A
D
O
C
B
D
B
O
C
A
由旋转得到:
平行四边形是中心对称图形,对角线的交点是对称中心
学
展
1.平行四边形是中心对称图形吗?如果是,你能找出它的对称中心吗?
合作探究
探究新知
学
展
(2)平行四边形的对边相等
A
D
C
B
证明:连接AC
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC,
∴ ∠BAC=∠DCA,∠DAC=∠BCA
∵ AC=CA
∴△ABC≌△CDA(ASA)
∴AB=CD,CB=AD
平行四边形对边相等
∵
∴
几何语言
已知: 四边形ABCD是平行四边形.
求证: AB=CD,BC=DA.
四边形ABCD是平行四边形.
AB=CD,BC=DA.
点评:要证明上述结论,可
以连接AC或BD,将平行四边形
转化为两个三角形,化未知为已知,渗透“转化思想”,突破难点。
探究新知
学
展
(3)平行四边形的对角相等
A
D
C
B
证明:连接AC
平行四边形对角相等
已知: 四边形ABCD是平行四边形.
求证: ∠A=∠C, ∠B=∠D.
∵
∴
几何语言
四边形ABCD是平行四边形.
∠A=∠C, ∠B=∠D
4
3
2
1
∵四边形ABCD是平行四边形
∴ AB=CD,BC=DA
又∵AC=AC
∴ △ABC≌△CDA
∴∠B=∠D
∵∠1= ∠2, ∠3= ∠4
∴∠1+∠4=∠2+∠3
即∠BAD=∠BCD
探究新知
学
展
(3)平行四边形的对角相等
A
D
C
B
还有其他的证明方法吗?
证明:
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC,
∴ ∠B+∠A=180°,
∠B+∠C=180°
∴ ∠A=∠C
同理可证 ∠B=∠D
1
或:∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴ ∠B =∠1,∠D =∠1
∴ ∠B =∠D
同理可证 ∠A=∠C
同时我们还可以得到邻角有怎样的关系?
邻角互补。
学以致用
学
例1 已知:如图,在 ABCD中,E,F是对角线AC上的两点,并且AE=CF
求证:BE=DF
证明:∵四边形ABCD是平行四边形
∴AB=CD,AB∥CD
∴∠BAE= ∠DCF
又∵AE=CF
∴ △ABE≌△CDF
∴BE=DF
温馨提示:证明边、角相等时,常用求三角形全等来解决。
A
C
D
B
E
F
变式训练:
练
A
C
D
B
E
F
已知:在□ ABCD中,BE⊥AC,DF⊥AC
垂足分别为E、F。 求证:BE=DF
证明:
∵四边形ABCD为平行四边形
∴AB=CD, AB∥CD
∴∠BAE= ∠DAF
∵BE⊥AC,DF⊥AC
∴∠BEA= ∠DFC= 90°
∴△ABE≌△CDF(AAS)
∴ BE=DF
巩固新知,火眼金睛
练
B
A
D
C
F
E
G
H
M
1、已知:AB∥CD∥GH ,AD∥BC∥EF
问:图中有几个平行四边形?
巩固新知,小试牛刀
练
2、小斌用根50m长的绳子围成一个平行四边形,其中
AD=16m,则BC=___ m, AB=____ m, CD=____m,
16
9
9
变式训练 : ABCD, 已知AC=12,△ABC的周长等于30,
则 ABCD的周长=?
巩固新知,小试牛刀
练
3、已知平行四边形一个内角的度数,能确定其它三个内角的度数吗?说说你的理由。
变式训练:在口ABCD 中,∠A 与∠B的度数之比为 5 :4
∠A、∠B、∠D的度数分别是 。
100°, 80°, 80°
反思:求角度数时,
要巧用对角相等,邻角互补。
课堂小结
理
同学们,在本节课的学习中,你对平行四边形的概念、性质及数学素养有哪些收获?(或者还有什么疑惑?和大家一起分享分享吧!
总结与升华
有关概念
性质
定义:两组对边分别平行的四边形
对角线:不相邻顶点间的线段
对称性:是中心对称图形对角线的交点是对称中心
对边:平行且相等
对角:相等
平行四边形
转化思想
理
课堂小结
4、有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
解:
∵AE∥BC、AB∥CF
∴四边形ABCD是平行四边形
∴∠B=∠D=60°,AD=BC=80cm
∵AE=60cm
∴DE=20cm
巩固练习
能力提升
练
5、学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
D1
D3
D2
A
B
C
能力拓展
练
1、在口ABCD 中,∠A=48°,BC=3cm,则∠B=___ ,∠C= ___AD=___
2、在口ABCD 中, ∠A与∠B 的度数之比为4:5,∠A= ___,∠B= ___ , ∠C= ___ ,∠D= ___ 。
3、如果平行四边形有一组对角互补,那么这个平行四边形的四个内角( )
A 都是锐角 B都是直角 C 都是钝角 D两个锐角,两个钝角
80°
80°
100°
100°
132°
48°
3cm
B
跟踪检测
你是最棒的
测
必做题:
选做题:
如图,在 ABCD中,点E,F分别在边CB,AD的延长线上,且BE=DF,EF分别与AB,CD交于点G,H,求证:AG=CH.
如图,在 ABCD中,点E,F分别在边CB,AD的延长线上,且BE=DF,EF分别与AB,CD交于点G,H,求证:AG=CH.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠A=∠C,
∴∠F=∠E.
∵BE=DF,所以AD+DF=CB+BE,
即AF=CE.
在△AGF和△CHE中,
∵∠A=∠C,AF=CE,∠F=∠E,
∴△AGF≌△CHE(ASA),
∴AG=CH.
练
分层作业,因材施教
必做:
课本习题5.1第1、2、3题
选做:如图,将平行四边形ABCO放置在平面直角坐标系xOy中,O为坐标原点,若点A的坐标是(6,0),点C的坐标是(1,4),则点B的坐标是 .
教师寄语
“学习数学要多做习题,边做边思索。
先知其然,然后知其所以然”
——苏步青(著名数学家)
5.1平行四边形的性质
鲁教版八年级上册第五章第一节
平行四边形
四边形
3.应用
1.概念
2.性质
学习目标
1. 理解并掌握平行四边形的定义及有关概念。
2. 经历探究的过程,理解与掌握平行四边形的性质及应用。
3.通过图形的变换探索平行四边形的性质及平行四边形的性质的应用。
有一块形状如图 所示的玻璃,小明不小心把EDF部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,聪明的你能根据测得的数据帮小明计算出DE的长度和∠D的度数吗?
巩固练习
创设情景,引入新知
情景导入
活动1 生活中的平行四边形
情景导入
活动1 生活中的平行四边形
探究新知
学
活动1:请同学将制作好的两个全等的三角形拿出来将它们相等的一组边重合,拼成一个四边形。
问题(1)这样的四边形能拼出几种?展示你所有的拼图结果
问题(2)观察拼出的四边形的对边有怎样的位置关系?说说你的理由。
拼图游戏
探究新知
展
活动2 成果展示
探究新知
学
平行四边形
从拼图可以得到什么启示?
小结:平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连接对角线转化为两个全等的三角形进行解题。
探究新知
学
平行四边形相关定义:
1、两组对边分别平行的四边形叫平行四边形。如图:四边形ABCD 是平行四边形,
记做□ ABCD ,读作平行四边形ABCD。
注意:平行四边形的表示要按一定的方向依次表示各顶点,不能有跳跃
D
A
B
C
2、平行四边形不相邻的两个顶点连成的线段叫对角线。
3、平行四边形相对的边称为 对边
相对的角称为 对角
火眼金睛
练
你能从以下图形中找出平行四边形吗?
1
2
3
4
5
两组对边分别平行,是平行四边形的一个主要特征。
探究新知
学
D
A
B
C
定义包括两重意思:
(1)如果两组对边分别平行,那么这个四边形就是平行四边形;
几何语言:
∵ AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
判定作用
或者 ∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
性质作用
合作探究
展
研
思考:问题(1)平行四边形是中心对称图形吗?
如果是,你能找到它的对称中心吗?
问题(2)平行四边形的对边有什么性质?
问题(3)平行四边形的对角有什么性质?
问题(4)平行四边形中相邻的两角有什么关系呢?
1、活动要求:采用度量、平移、旋转的方法探究平行四边形的性质。
2、学生利用学具(全等的三角形纸板、平行四边形纸板各一对,格尺、量角器,图钉)小组合作探究
●
A
D
O
C
B
D
B
O
C
A
由旋转得到:
平行四边形是中心对称图形,对角线的交点是对称中心
学
展
1.平行四边形是中心对称图形吗?如果是,你能找出它的对称中心吗?
合作探究
探究新知
学
展
(2)平行四边形的对边相等
A
D
C
B
证明:连接AC
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC,
∴ ∠BAC=∠DCA,∠DAC=∠BCA
∵ AC=CA
∴△ABC≌△CDA(ASA)
∴AB=CD,CB=AD
平行四边形对边相等
∵
∴
几何语言
已知: 四边形ABCD是平行四边形.
求证: AB=CD,BC=DA.
四边形ABCD是平行四边形.
AB=CD,BC=DA.
点评:要证明上述结论,可
以连接AC或BD,将平行四边形
转化为两个三角形,化未知为已知,渗透“转化思想”,突破难点。
探究新知
学
展
(3)平行四边形的对角相等
A
D
C
B
证明:连接AC
平行四边形对角相等
已知: 四边形ABCD是平行四边形.
求证: ∠A=∠C, ∠B=∠D.
∵
∴
几何语言
四边形ABCD是平行四边形.
∠A=∠C, ∠B=∠D
4
3
2
1
∵四边形ABCD是平行四边形
∴ AB=CD,BC=DA
又∵AC=AC
∴ △ABC≌△CDA
∴∠B=∠D
∵∠1= ∠2, ∠3= ∠4
∴∠1+∠4=∠2+∠3
即∠BAD=∠BCD
探究新知
学
展
(3)平行四边形的对角相等
A
D
C
B
还有其他的证明方法吗?
证明:
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC,
∴ ∠B+∠A=180°,
∠B+∠C=180°
∴ ∠A=∠C
同理可证 ∠B=∠D
1
或:∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴ ∠B =∠1,∠D =∠1
∴ ∠B =∠D
同理可证 ∠A=∠C
同时我们还可以得到邻角有怎样的关系?
邻角互补。
学以致用
学
例1 已知:如图,在 ABCD中,E,F是对角线AC上的两点,并且AE=CF
求证:BE=DF
证明:∵四边形ABCD是平行四边形
∴AB=CD,AB∥CD
∴∠BAE= ∠DCF
又∵AE=CF
∴ △ABE≌△CDF
∴BE=DF
温馨提示:证明边、角相等时,常用求三角形全等来解决。
A
C
D
B
E
F
变式训练:
练
A
C
D
B
E
F
已知:在□ ABCD中,BE⊥AC,DF⊥AC
垂足分别为E、F。 求证:BE=DF
证明:
∵四边形ABCD为平行四边形
∴AB=CD, AB∥CD
∴∠BAE= ∠DAF
∵BE⊥AC,DF⊥AC
∴∠BEA= ∠DFC= 90°
∴△ABE≌△CDF(AAS)
∴ BE=DF
巩固新知,火眼金睛
练
B
A
D
C
F
E
G
H
M
1、已知:AB∥CD∥GH ,AD∥BC∥EF
问:图中有几个平行四边形?
巩固新知,小试牛刀
练
2、小斌用根50m长的绳子围成一个平行四边形,其中
AD=16m,则BC=___ m, AB=____ m, CD=____m,
16
9
9
变式训练 : ABCD, 已知AC=12,△ABC的周长等于30,
则 ABCD的周长=?
巩固新知,小试牛刀
练
3、已知平行四边形一个内角的度数,能确定其它三个内角的度数吗?说说你的理由。
变式训练:在口ABCD 中,∠A 与∠B的度数之比为 5 :4
∠A、∠B、∠D的度数分别是 。
100°, 80°, 80°
反思:求角度数时,
要巧用对角相等,邻角互补。
课堂小结
理
同学们,在本节课的学习中,你对平行四边形的概念、性质及数学素养有哪些收获?(或者还有什么疑惑?和大家一起分享分享吧!
总结与升华
有关概念
性质
定义:两组对边分别平行的四边形
对角线:不相邻顶点间的线段
对称性:是中心对称图形对角线的交点是对称中心
对边:平行且相等
对角:相等
平行四边形
转化思想
理
课堂小结
4、有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
解:
∵AE∥BC、AB∥CF
∴四边形ABCD是平行四边形
∴∠B=∠D=60°,AD=BC=80cm
∵AE=60cm
∴DE=20cm
巩固练习
能力提升
练
5、学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
D1
D3
D2
A
B
C
能力拓展
练
1、在口ABCD 中,∠A=48°,BC=3cm,则∠B=___ ,∠C= ___AD=___
2、在口ABCD 中, ∠A与∠B 的度数之比为4:5,∠A= ___,∠B= ___ , ∠C= ___ ,∠D= ___ 。
3、如果平行四边形有一组对角互补,那么这个平行四边形的四个内角( )
A 都是锐角 B都是直角 C 都是钝角 D两个锐角,两个钝角
80°
80°
100°
100°
132°
48°
3cm
B
跟踪检测
你是最棒的
测
必做题:
选做题:
如图,在 ABCD中,点E,F分别在边CB,AD的延长线上,且BE=DF,EF分别与AB,CD交于点G,H,求证:AG=CH.
如图,在 ABCD中,点E,F分别在边CB,AD的延长线上,且BE=DF,EF分别与AB,CD交于点G,H,求证:AG=CH.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠A=∠C,
∴∠F=∠E.
∵BE=DF,所以AD+DF=CB+BE,
即AF=CE.
在△AGF和△CHE中,
∵∠A=∠C,AF=CE,∠F=∠E,
∴△AGF≌△CHE(ASA),
∴AG=CH.
练
分层作业,因材施教
必做:
课本习题5.1第1、2、3题
选做:如图,将平行四边形ABCO放置在平面直角坐标系xOy中,O为坐标原点,若点A的坐标是(6,0),点C的坐标是(1,4),则点B的坐标是 .
教师寄语
“学习数学要多做习题,边做边思索。
先知其然,然后知其所以然”
——苏步青(著名数学家)
