2022-2023学年京改版八年级数学上册12.6 等腰三角形课堂提升训练(含答案解析)
文档属性
| 名称 | 2022-2023学年京改版八年级数学上册12.6 等腰三角形课堂提升训练(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 665.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-24 21:44:55 | ||
图片预览



文档简介
2022-2023学年度北京课改版版八年级数学上册
课堂提升训练
第十二章 三角形
三 等腰三角形与直角三角形
12.6 等腰三角形
基础过关全练
知识点1 等腰三角形及相关概念
1.如图所示,D在AC上,AB=AC,AD=DB,请指出图中的等腰三角形,以及它们的腰、底边、顶角及底角.
知识点2 等腰三角形的性质
2.如图,△ABC中,AB=AC,AD⊥BC,下列结论不一定正确的是( )
A.∠B=∠C
B.BD=CD
C.AB=2BD
D.AD平分∠BAC
3. 等腰三角形的一个内角为70°,则另外两个内角的度数分别是( )
A.55°,55° B.70°,40°
C.70°,40°或70°,55° D.55°,55°或70°,40°
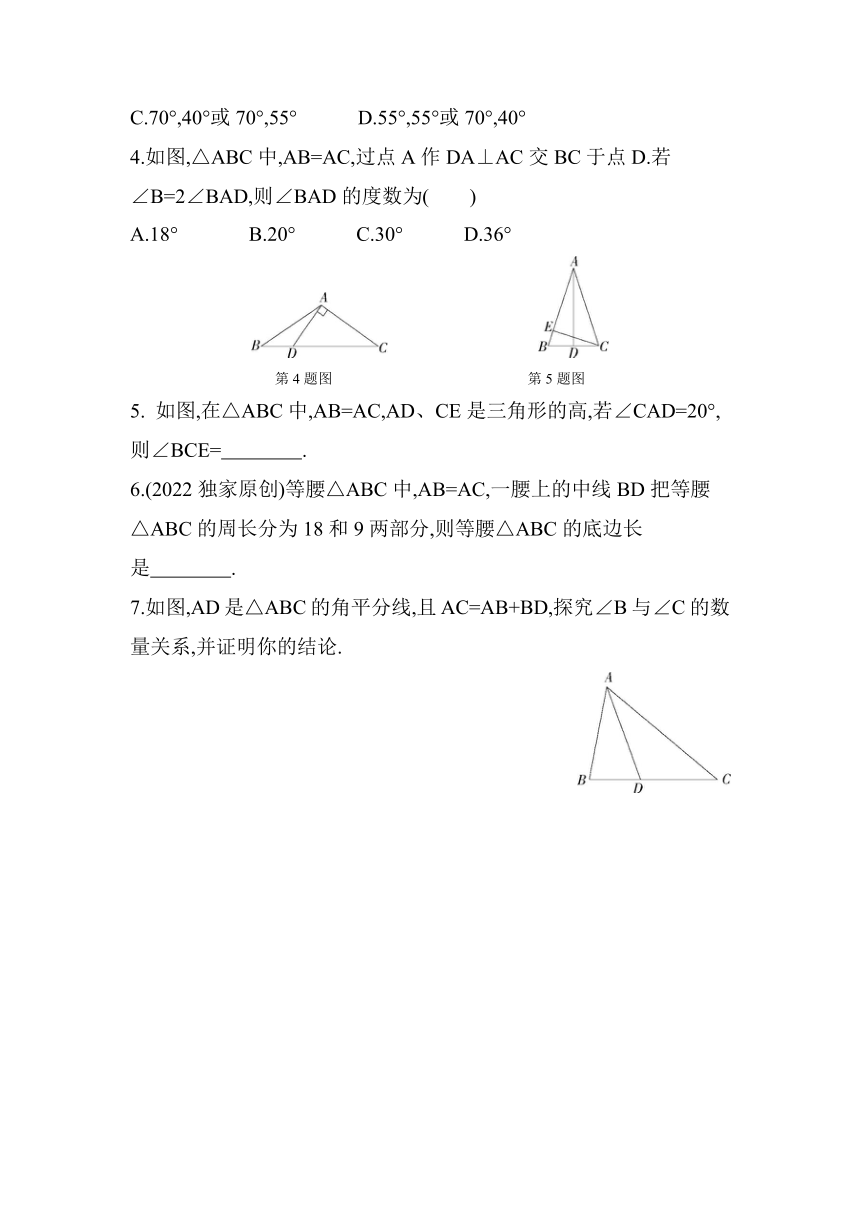
4.如图,△ABC中,AB=AC,过点A作DA⊥AC交BC于点D.若∠B=2∠BAD,则∠BAD的度数为( )
A.18° B.20° C.30° D.36°
第4题图 第5题图
5. 如图,在△ABC中,AB=AC,AD、CE是三角形的高,若∠CAD=20°,则∠BCE= .
6.(2022独家原创)等腰△ABC中,AB=AC,一腰上的中线BD把等腰△ABC的周长分为18和9两部分,则等腰△ABC的底边长是 .
7.如图,AD是△ABC的角平分线,且AC=AB+BD,探究∠B与∠C的数量关系,并证明你的结论.
知识点3 等边三角形的性质
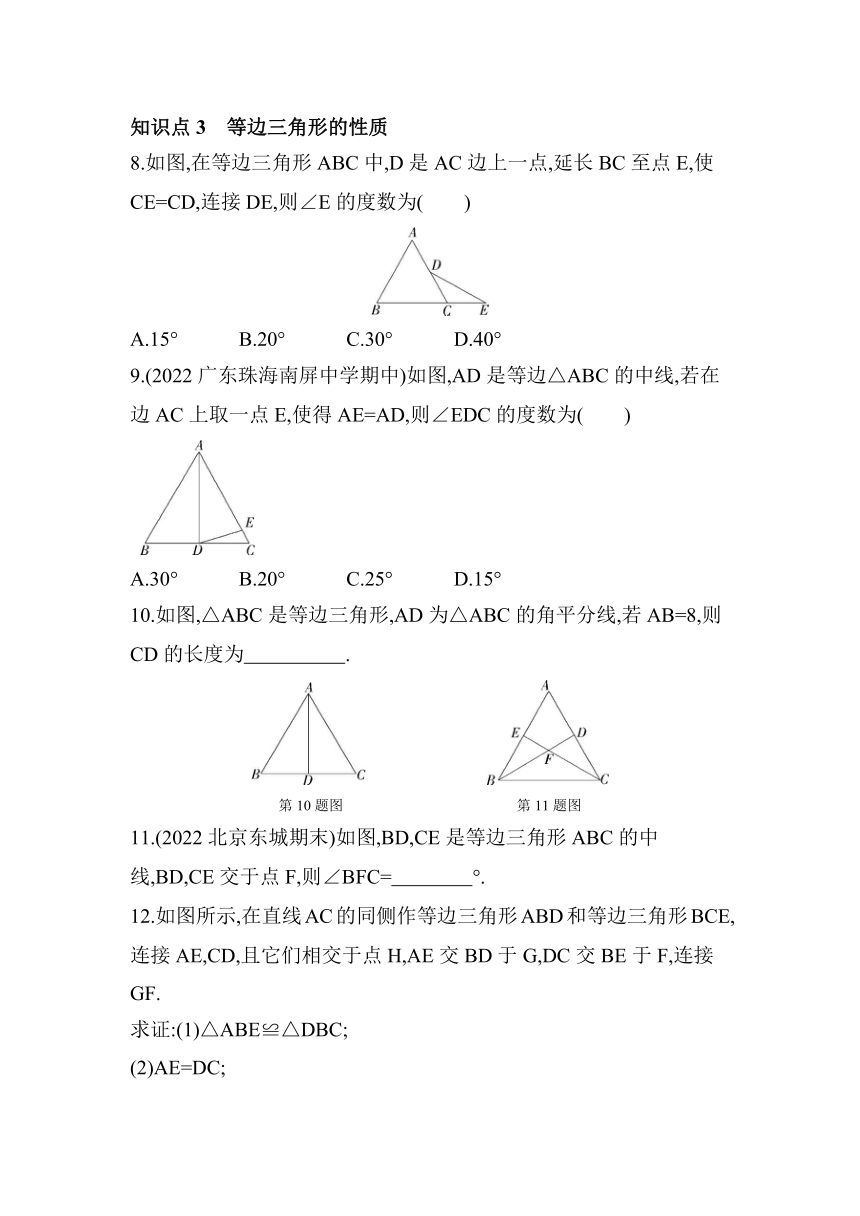
8.如图,在等边三角形ABC中,D是AC边上一点,延长BC至点E,使CE=CD,连接DE,则∠E的度数为( )
A.15° B.20° C.30° D.40°
9.(2022广东珠海南屏中学期中)如图,AD是等边△ABC的中线,若在边AC上取一点E,使得AE=AD,则∠EDC的度数为( )
A.30° B.20° C.25° D.15°
10.如图,△ABC是等边三角形,AD为△ABC的角平分线,若AB=8,则CD的长度为 .
第10题图 第11题图
11.(2022北京东城期末)如图,BD,CE是等边三角形ABC的中线,BD,CE交于点F,则∠BFC= °.
12.如图所示,在直线AC的同侧作等边三角形ABD和等边三角形BCE,连接AE,CD,且它们相交于点H,AE交BD于G,DC交BE于F,连接GF.
求证:(1)△ABE≌△DBC;
(2)AE=DC;
(3)AE与DC所夹的锐角为60°;
(4)△ABG≌△DBF;
(5)GF∥AC.
知识点4 等腰三角形的判定
13.(2022吉林长春期末)如图,在5×5的正方形网格中,每个小正方形的顶点称为格点,点A、B均在格点上.要在格点上确定一点C,连接AC和BC,使△ABC是等腰三角形,则网格中满足条件的点C的个数是( )
A.5 B.6 C.7 D.8
14.(2021安徽合肥庐阳期末)如图,在△ABC中,AB=AC,∠BAC=36°,BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF.写出图中所有等腰三角形: .
15.(2022河北定州期末)如图,在△ABC中,AB=AC,M、N分别是AB、AC边上的点,并且MN∥BC.
(1)求证:△AMN是等腰三角形;
(2)点P是MN上的一点,并且BP平分∠ABC,求证:△BPM是等腰三角形.
知识点5 等边三角形的判定
16.如图,小马师傅用自制的工具测量零件内部的宽度AB,已知OA=OB=50 cm,∠DOC=60°,则零件内部的宽度AB= .
17.(教材P104变式题)如图,延长△ABC的各边,使得BF=AC,AE=CD=AB,连接DE、EF、FD,得到等边三角形DEF.
求证:(1)△AEF≌△CDE;
(2)△ABC为等边三角形.
能力提升全练
18.(2021湖南益阳中考,7,)如图,AB∥CD,△ACE为等边三角形,∠DCE=40°,则∠EAB的度数为( )
A.40° B.30° C.20° D.15°
19.(2021广东深圳罗湖期末,6,)下列推理中,不能判定△ABC是等边三角形的是( )
A.∠A=∠B=∠C B.AB=AC,∠B=60°
C.∠A=60°,∠B=60° D.AB=AC且∠B=∠C
20.(2021北京五十七中期中,10,)如图所示的正方形网格中,网格线的交点称为格点,已知A,B是两个格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则符合条件的点C的个数是( )
A.6 B.7 C.8 D.9
第20题图 第21题图
21. 如图,等边三角形纸片ABC的边长为6,E,F是边BC上的三等分点.分别过点E,F沿着平行于BA,CA方向各剪一刀,则剪下的△DEF的周长是 .
22. 已知等腰三角形一腰上的高与另一腰的夹角为35°,则这个等腰三角形顶角的度数为 .
23.(2018吉林中考,14,)我们规定:等腰三角形的顶角度数与一个底角度数的比值叫做等腰三角形的“特征值”,记作k.若k=,则该等腰三角形的顶角为 度.
24.(2021黑龙江牡丹江中考,6,)过等腰三角形顶角顶点的一条直线,将该等腰三角形分成了两个小等腰三角形,则原等腰三角形底角的度数为 .
25. 如图,已知点D,E分别是△ABC的边BA,BC延长线上的点,作∠DAC的平分线AF,若AF∥BC.
(1)求证:△ABC是等腰三角形;
(2)作∠ACE的平分线交AF于点G,若∠B=40°,求∠AGC的度数.
26.(2022北京师大附属实验中学期末,23,)如图,AD∥BC,AE平分∠BAD,点E为DC中点,求证:AD+BC=AB.
27.(2021浙江绍兴中考,21,)如图,在△ABC中,∠A=40°,点D,E分别在边AB,AC上,BD=BC=CE,连接CD,BE.
(1)若∠ABC=80°,求∠BDC,∠ABE的度数;
(2)写出∠BEC与∠BDC之间的关系,并说明理由.
28. 问题:如图,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC.若∠BAE=90°,∠B=45°,求∠DAC的度数.
答案:∠DAC=45°.
思考:
(1)如果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗 说明理由;
(2)如果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数(用含n的代数式表示).
素养探究全练
29.[逻辑推理]在△ABC中,AB=AC,∠ABC、∠ACB的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.
(1)如图1,图中等腰三角形为 ,猜想:EF、BE、CF之间有怎样的关系,并说明理由;
(2)如图2,若AB≠AC,则图中等腰三角形是 ,(1)中的EF、BE、CF之间的数量关系还存在吗 请说明理由;
(3)如图3,△ABC中∠ABC的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.图中等腰三角形是 ,写出EF、BE、CF之间的数量关系,并说明理由.
图1 图2 图3
答案全解全析
基础过关全练
1.解析 等腰三角形有△ABC、△ABD;△ABC的腰是AB、AC,底边是BC,顶角是∠A,底角是∠ABC、∠ACB;△ABD的腰是AD、BD,底边是AB,顶角是∠ADB,底角是∠A、∠ABD.
2.C ∵AB=AC,AD⊥BC,∴∠B=∠C,BD=DC,AD平分∠BAC,故A、B、D选项正确,无法确定AB=2BD,故C选项错误.
3.D 分情况讨论:(1)当等腰三角形的顶角为70°时,底角=(180°-70°)÷2=55°;(2)当等腰三角形的底角为70°时,另外一个底角为70°,顶角为180°-70°-70°=40°.故选D.
4.A ∵AB=AC,∴∠B=∠C,
∵∠B=2∠BAD,∴∠C=2∠BAD,
∵DA⊥AC,∴∠DAC=90°,
∵∠B+∠C+∠BAC=180°,∠BAC=∠BAD+90°,
∴2∠BAD+2∠BAD+∠BAD+90°=180°,
∴∠BAD=18°.
5.20°
解析 ∵AB=AC,AD是三角形的高,
∴∠BAD=∠CAD=20°,∠ABC=∠ACB,
∴∠ABC==70°.
∵CE是三角形的高,∴∠CEB=90°,∴∠BCE=20°.
6.3
解析 根据题意画出图形,如图,
设AB=AC=2x,BC=y,
∵BD是腰上的中线,∴AD=DC=x,
分情况讨论:①当AB+AD=18,BC+CD=9时,解得此时△ABC三边长分别为12,12,3,符合三角形的三边关系;②当AB+AD=9,BC+CD=18时,解得此时△ABC三边长分别为6,6,15,不符合三角形的三边关系,舍去.
综上,等腰△ABC的底边长为3.
7.解析 ∠B=2∠C.
证明:如图,在AC上截取AE=AB,连接DE,∵AD是△ABC的角平分线,∴∠BAD=∠EAD,∵AB=AE,AD=AD,∴△ABD≌△AED(SAS),
∴BD=ED,∠B=∠AED,
∵AC=AB+BD,AC=AE+CE,∴BD=CE.
∴DE=CE,∴∠C=∠EDC,
∴∠AED=∠EDC+∠C=2∠C.
∴∠B=2∠C.
8.C ∵△ABC是等边三角形,∴∠ACB=60°.∵CD=CE,∴∠E=∠CDE.∵∠ACB=∠E+∠CDE=2∠E=60°,∴∠E=30°.
9.D ∵△ABC为等边三角形,∴∠BAC=60°,
∵AD是等边△ABC的中线,
∴AD⊥BC,∠CAD=∠BAC=30°,
∵AE=AD,∴∠ADE=∠AED,
∵∠ADE+∠AED+∠CAD=180°,
∴∠ADE+∠ADE+30°=180°,
∴∠ADE=75°,∴∠EDC=90°-75°=15°.
10.4
解析 ∵△ABC为等边三角形,AB=8,∴BC=8.
∵AD为△ABC的角平分线,∴BD=CD,∴CD=4.
11.120
解析 ∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵BD,CE是等边三角形ABC的中线,
∴BD平分∠ABC,CE平分∠ACB,
∴∠FBC=∠ABC=30°,∠FCB=∠ACB=30°,
∴∠BFC=180°-∠FBC-∠FCB=120°.
12.证明 (1)∵△ABD、△BCE为等边三角形,
∴AB=DB,∠ABD=∠CBE=60°,BE=BC,
∴∠ABE=∠DBC,∠DBE=60°.
在△ABE和△DBC中,
∴△ABE≌△DBC(SAS).
(2)由(1)知△ABE≌△DBC,∴AE=DC.
(3)由(1)知△ABE≌△DBC,∴∠BAE=∠BDC.
∵∠DGH=∠AGB,∠DHA=180°-∠BDC-∠DGH,∠DBA=180°-∠BAE-∠AGB,
∴∠DHA=∠DBA=60°,
∴AE与DC所夹的锐角为60°.
(4)由(1)知△ABE≌△DBC,∴∠BAG=∠BDF.
在△ABG和△DBF中,
∴△ABG≌△DBF(ASA).
(5)由(4)知△ABG≌△DBF,∴BG=BF.
∴∠GFB=∠FGB,又∵∠GBF=60°,
∴∠GFB==60°,
∴∠GFB=∠FBC,∴GF∥AC.
13.B 如图:
网格中满足条件的点C的个数为6,故选B.
14.△ABD,△BCD,△ABC,△ACF,△ABF
解析 ∵AB=AC,∠BAC=36°,
∴∠ABC=∠ACB=72°,△ABC是等腰三角形,
∵BD是∠ABC的平分线,
∴∠ABD=∠CBD=36°=∠BAC,
∴AD=BD,∠BDC=∠BAC+∠ABD=72°=∠ACB,
∴△ABD是等腰三角形,BD=BC,
∴△BDC是等腰三角形,
∵AD=BD,E是AB的中点,
∴DE⊥AB,∴∠FEA=∠FEB=90°,
∵AE=BE,EF=EF,∴△AEF≌△BEF(SAS),
∴AF=BF,∠FAB=∠FBA=72°,
∴△ABF是等腰三角形,∠AFB=180°-72°-72°=36°,∠FAC=72°-36°=36°,∴∠AFB=∠FAC,
∴AC=CF,
∴△ACF是等腰三角形.
15.证明 (1)∵AB=AC,∴∠ABC=∠C,
∵MN∥BC,
∴∠AMN=∠ABC,∠ANM=∠C,
∴∠AMN=∠ANM,∴AM=AN,
∴△AMN是等腰三角形.
(2)∵BP平分∠ABC,∴∠MBP=∠CBP,
∵MN∥BC,∴∠MPB=∠CBP,
∴∠MBP=∠MPB,∴MB=MP,
∴△BPM是等腰三角形.
16.50 cm
解析 ∵∠DOC=60°,∴∠AOB=60°.∵OA=OB,∴△OAB是等边三角形,∴AB=OA=OB=50 cm.
17.证明 (1)∵BF=AC,AB=AE,∴FA=EC.
∵△DEF是等边三角形,∴EF=DE.
∵AE=CD,∴△AEF≌△CDE(SSS).
(2)由(1)知△AEF≌△CDE,∴∠FEA=∠EDC,
∵△DEF是等边三角形,∴∠DEF=60°.
∵∠BCA=∠EDC+∠DEC=∠FEA+∠DEC=∠DEF,
∴∠BCA=60°,同理可得∠BAC=60°,∴∠ABC=60°,
∴△ABC是等边三角形.
能力提升全练
18.C 根据平行线的性质可得∠DCA+∠CAB=180°,即∠DCE+∠ECA+∠EAC+∠EAB=180°,由△ACE为等边三角形得∠ECA=∠EAC=60°,所以∠EAB=180°-40°-60°-60°=20°.故选C.
19.D A.由“三个角都相等的三角形是等边三角形”可以判定△ABC是等边三角形,故本选项不符合题意.B.由“有一个角是60°的等腰三角形是等边三角形”可以判定△ABC是等边三角形,故本选项不符合题意.C.由“∠A=60°,∠B=60°”可以得到“∠A=∠B=∠C=60°”,则由“三个角都相等的三角形是等边三角形”可以判定△ABC是等边三角形,故本选项不符合题意.D.由“AB=AC且∠B=∠C”只能判定△ABC是等腰三角形,故本选项符合题意.故选D.
20.C ①当AB为等腰△ABC的底边时,符合条件的C点有4个;
②当AB为等腰△ABC的一个腰时,符合条件的C点有4个.
综上,符合条件的点C有8个.
21.6
解析 ∵等边三角形纸片ABC的边长为6,E,F是边BC上的三等分点,∴EF=2,
∵△ABC是等边三角形,∴∠B=∠C=60°,
∵DE∥AB,DF∥AC,
∴∠DEF=∠B=60°,∠DFE=∠C=60°,
∴∠D=∠DEF=∠DFE=60°,
∴△DEF是等边三角形,
∴DE=DF=EF=2,
∴剪下的△DEF的周长是2×3=6.
22.55°或125°
解析 分两种情况讨论:
①当一腰上的高在三角形内部时,如图1,
∵BD⊥AC,∴∠ADB=90°.
∵∠ABD=35°,∴∠A=180°-35°-90°=55°.
图1
②当一腰上的高在三角形外部时,如图2,
图2
∵BD⊥AC,∴∠BDC=90°.
∵∠ABD=35°,∴∠BAC=90°+35°=125°.
综上所述,这个等腰三角形顶角的度数为55°或125°.
23.36
解析 设等腰三角形顶角的度数为α,则底角度数为90°-α,由题意得α=,解得α=36°.
24.36°或45°
解析 分两种情况讨论:
(1)如图1,△ABC中,AB=AC,AD=BD=CD,
∴∠B=∠C=∠DAC=∠DAB,
∴∠BAC=2∠B,
∵∠BAC+∠B+∠C=180°,
∴4∠B=180°,∴∠B=45°.
(2)如图2,△ABC中,AB=AC,BD=AD,AC=CD,
∴∠B=∠C=∠BAD,∠CDA=∠CAD,
∴∠CAD=∠CDA=∠ABC+∠BAD=2∠B,
∴∠BAC=3∠B,
∵∠BAC+∠B+∠C=180°,
∴5∠B=180°,∴∠B=36°.
综上,原等腰三角形底角的度数为36°或45°.
图1 图2
25.解析 (1)证明:∵AF平分∠DAC,∴∠DAF=∠CAF,∵AF∥BC,∴∠DAF=∠B,∠CAF=∠ACB,
∴∠B=∠ACB,∴AB=AC,∴△ABC是等腰三角形.
(2)由(1)知∠B=∠ACB,
∵∠B=40°,∴∠ACB=∠B=40°,∴∠BAC=100°,
∴∠ACE=∠BAC+∠B=140°,∵CG平分∠ACE,
∴∠ECG=∠ACE=70°,∵AF∥BC,∴∠AGC=∠ECG=70°.
26.证明 如图,分别延长AE,BC交于点F,
∵AD∥BC,∴∠DAE=∠CFE,
∵点E是DC的中点,∴ED=CE,
在△ADE与△FCE中,
∴△ADE≌△FCE(AAS),
∴AD=CF,
∵AE平分∠BAD,∴∠DAF=∠BAF,
∵∠DAF=∠F,∴∠BAF=∠F,∴AB=BF,
∴AB=BF=BC+CF=BC+AD.
27.解析 (1)∵∠ABC=80°,BD=BC,
∴∠BDC=∠BCD=×(180°-80°)=50°,
∵∠A+∠ABC+∠ACB=180°,∠A=40°,
∴∠ACB=180°-40°-80°=60°,
∵CE=BC,∴△BCE是等边三角形,
∴∠EBC=60°,
∴∠ABE=∠ABC-∠EBC=80°-60°=20°.
(2)∠BEC+∠BDC=110°,
理由:设∠BEC=α,∠BDC=β,
则α=∠A+∠ABE=40°+∠ABE,
∴∠ABE=α-40°,
∵CE=BC,∴∠CBE=∠BEC=α,
∴∠CBD=α+α-40°=2α-40°,
∵BD=BC,∴∠BCD=∠BDC=β,
在△BCD中,∠CBD+∠BDC+∠BCD=180°,
∴2α-40°+β+β=180°,∴α+β=110°,
∴∠BEC+∠BDC=110°.
28.解析 (1)∠DAC的度数不会改变.理由:
∵EA=EC,∴∠EAC=∠C,
∵BA=BD,∴∠BAD=∠BDA,
∵∠BAE=90°,
∴∠B=90°-∠AED=90°-2∠C,
∴∠BAD=(180°-∠B)=[180°-(90°-2∠C)]=45°+∠C,
∴∠DAE=90°-∠BAD=90°-(45°+∠C)=45°-∠C,
∵∠EAC=∠C,
∴∠DAC=∠DAE+∠CAE=45°-∠C+∠C=45°.
(2)设∠ABC=m°,
∵AB=DB,∴∠BAD=(180°-m°)=90°-m°,
∵∠BAE=n°,∴∠AEB=180°-n°-m°,
∴∠DAE=n°-∠BAD=n°-90°+m°,
∵EA=EC,∴∠CAE=∠AEB=90°-n°-m°,
∴∠DAC=∠DAE+∠CAE=n°-90°+m°+90°-n°-m°=n°.
素养探究全练
29.解析 (1)图中等腰三角形为△AEF、△OEB、△OFC、△OBC、△ABC.
EF、BE、FC之间的数量关系是EF=BE+CF.
理由:∵BO、CO分别平分∠ABC、∠ACB,
∴∠ABO=∠OBC,∠ACO=∠OCB,
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCB,
∴∠EOB=∠EBO,∠FOC=∠FCO,
∴EO=EB,FO=FC,
∴EF=EO+OF=BE+CF.
(2)图中等腰三角形是△EOB、△FOC,(1)中的EF、BE、CF之间的数量关系仍然成立.
理由:∵BO、CO分别平分∠ABC、∠ACB,
∴∠ABO=∠OBC,∠ACO=∠OCB,
∵EF∥BC,∴∠EOB=∠OBC,∠FOC=∠OCB,
∴∠EOB=∠EBO,∠FOC=∠FCO,
∴EO=EB,FO=FC,
∴EF=EO+OF=BE+CF.
(3)图中等腰三角形是△EOB和△FOC,EF=BE-FC.理由:同(1)可证得EO=EB,
∵EO∥BC,∴∠FOC=∠OCG,
∵CO平分∠ACG,
∴∠ACO=∠OCG,∴∠FOC=∠FCO,∴FO=FC,
∴EF=EO-FO=BE-FC.
课堂提升训练
第十二章 三角形
三 等腰三角形与直角三角形
12.6 等腰三角形
基础过关全练
知识点1 等腰三角形及相关概念
1.如图所示,D在AC上,AB=AC,AD=DB,请指出图中的等腰三角形,以及它们的腰、底边、顶角及底角.
知识点2 等腰三角形的性质
2.如图,△ABC中,AB=AC,AD⊥BC,下列结论不一定正确的是( )
A.∠B=∠C
B.BD=CD
C.AB=2BD
D.AD平分∠BAC
3. 等腰三角形的一个内角为70°,则另外两个内角的度数分别是( )
A.55°,55° B.70°,40°
C.70°,40°或70°,55° D.55°,55°或70°,40°
4.如图,△ABC中,AB=AC,过点A作DA⊥AC交BC于点D.若∠B=2∠BAD,则∠BAD的度数为( )
A.18° B.20° C.30° D.36°
第4题图 第5题图
5. 如图,在△ABC中,AB=AC,AD、CE是三角形的高,若∠CAD=20°,则∠BCE= .
6.(2022独家原创)等腰△ABC中,AB=AC,一腰上的中线BD把等腰△ABC的周长分为18和9两部分,则等腰△ABC的底边长是 .
7.如图,AD是△ABC的角平分线,且AC=AB+BD,探究∠B与∠C的数量关系,并证明你的结论.
知识点3 等边三角形的性质
8.如图,在等边三角形ABC中,D是AC边上一点,延长BC至点E,使CE=CD,连接DE,则∠E的度数为( )
A.15° B.20° C.30° D.40°
9.(2022广东珠海南屏中学期中)如图,AD是等边△ABC的中线,若在边AC上取一点E,使得AE=AD,则∠EDC的度数为( )
A.30° B.20° C.25° D.15°
10.如图,△ABC是等边三角形,AD为△ABC的角平分线,若AB=8,则CD的长度为 .
第10题图 第11题图
11.(2022北京东城期末)如图,BD,CE是等边三角形ABC的中线,BD,CE交于点F,则∠BFC= °.
12.如图所示,在直线AC的同侧作等边三角形ABD和等边三角形BCE,连接AE,CD,且它们相交于点H,AE交BD于G,DC交BE于F,连接GF.
求证:(1)△ABE≌△DBC;
(2)AE=DC;
(3)AE与DC所夹的锐角为60°;
(4)△ABG≌△DBF;
(5)GF∥AC.
知识点4 等腰三角形的判定
13.(2022吉林长春期末)如图,在5×5的正方形网格中,每个小正方形的顶点称为格点,点A、B均在格点上.要在格点上确定一点C,连接AC和BC,使△ABC是等腰三角形,则网格中满足条件的点C的个数是( )
A.5 B.6 C.7 D.8
14.(2021安徽合肥庐阳期末)如图,在△ABC中,AB=AC,∠BAC=36°,BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF.写出图中所有等腰三角形: .
15.(2022河北定州期末)如图,在△ABC中,AB=AC,M、N分别是AB、AC边上的点,并且MN∥BC.
(1)求证:△AMN是等腰三角形;
(2)点P是MN上的一点,并且BP平分∠ABC,求证:△BPM是等腰三角形.
知识点5 等边三角形的判定
16.如图,小马师傅用自制的工具测量零件内部的宽度AB,已知OA=OB=50 cm,∠DOC=60°,则零件内部的宽度AB= .
17.(教材P104变式题)如图,延长△ABC的各边,使得BF=AC,AE=CD=AB,连接DE、EF、FD,得到等边三角形DEF.
求证:(1)△AEF≌△CDE;
(2)△ABC为等边三角形.
能力提升全练
18.(2021湖南益阳中考,7,)如图,AB∥CD,△ACE为等边三角形,∠DCE=40°,则∠EAB的度数为( )
A.40° B.30° C.20° D.15°
19.(2021广东深圳罗湖期末,6,)下列推理中,不能判定△ABC是等边三角形的是( )
A.∠A=∠B=∠C B.AB=AC,∠B=60°
C.∠A=60°,∠B=60° D.AB=AC且∠B=∠C
20.(2021北京五十七中期中,10,)如图所示的正方形网格中,网格线的交点称为格点,已知A,B是两个格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则符合条件的点C的个数是( )
A.6 B.7 C.8 D.9
第20题图 第21题图
21. 如图,等边三角形纸片ABC的边长为6,E,F是边BC上的三等分点.分别过点E,F沿着平行于BA,CA方向各剪一刀,则剪下的△DEF的周长是 .
22. 已知等腰三角形一腰上的高与另一腰的夹角为35°,则这个等腰三角形顶角的度数为 .
23.(2018吉林中考,14,)我们规定:等腰三角形的顶角度数与一个底角度数的比值叫做等腰三角形的“特征值”,记作k.若k=,则该等腰三角形的顶角为 度.
24.(2021黑龙江牡丹江中考,6,)过等腰三角形顶角顶点的一条直线,将该等腰三角形分成了两个小等腰三角形,则原等腰三角形底角的度数为 .
25. 如图,已知点D,E分别是△ABC的边BA,BC延长线上的点,作∠DAC的平分线AF,若AF∥BC.
(1)求证:△ABC是等腰三角形;
(2)作∠ACE的平分线交AF于点G,若∠B=40°,求∠AGC的度数.
26.(2022北京师大附属实验中学期末,23,)如图,AD∥BC,AE平分∠BAD,点E为DC中点,求证:AD+BC=AB.
27.(2021浙江绍兴中考,21,)如图,在△ABC中,∠A=40°,点D,E分别在边AB,AC上,BD=BC=CE,连接CD,BE.
(1)若∠ABC=80°,求∠BDC,∠ABE的度数;
(2)写出∠BEC与∠BDC之间的关系,并说明理由.
28. 问题:如图,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC.若∠BAE=90°,∠B=45°,求∠DAC的度数.
答案:∠DAC=45°.
思考:
(1)如果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗 说明理由;
(2)如果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数(用含n的代数式表示).
素养探究全练
29.[逻辑推理]在△ABC中,AB=AC,∠ABC、∠ACB的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.
(1)如图1,图中等腰三角形为 ,猜想:EF、BE、CF之间有怎样的关系,并说明理由;
(2)如图2,若AB≠AC,则图中等腰三角形是 ,(1)中的EF、BE、CF之间的数量关系还存在吗 请说明理由;
(3)如图3,△ABC中∠ABC的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.图中等腰三角形是 ,写出EF、BE、CF之间的数量关系,并说明理由.
图1 图2 图3
答案全解全析
基础过关全练
1.解析 等腰三角形有△ABC、△ABD;△ABC的腰是AB、AC,底边是BC,顶角是∠A,底角是∠ABC、∠ACB;△ABD的腰是AD、BD,底边是AB,顶角是∠ADB,底角是∠A、∠ABD.
2.C ∵AB=AC,AD⊥BC,∴∠B=∠C,BD=DC,AD平分∠BAC,故A、B、D选项正确,无法确定AB=2BD,故C选项错误.
3.D 分情况讨论:(1)当等腰三角形的顶角为70°时,底角=(180°-70°)÷2=55°;(2)当等腰三角形的底角为70°时,另外一个底角为70°,顶角为180°-70°-70°=40°.故选D.
4.A ∵AB=AC,∴∠B=∠C,
∵∠B=2∠BAD,∴∠C=2∠BAD,
∵DA⊥AC,∴∠DAC=90°,
∵∠B+∠C+∠BAC=180°,∠BAC=∠BAD+90°,
∴2∠BAD+2∠BAD+∠BAD+90°=180°,
∴∠BAD=18°.
5.20°
解析 ∵AB=AC,AD是三角形的高,
∴∠BAD=∠CAD=20°,∠ABC=∠ACB,
∴∠ABC==70°.
∵CE是三角形的高,∴∠CEB=90°,∴∠BCE=20°.
6.3
解析 根据题意画出图形,如图,
设AB=AC=2x,BC=y,
∵BD是腰上的中线,∴AD=DC=x,
分情况讨论:①当AB+AD=18,BC+CD=9时,解得此时△ABC三边长分别为12,12,3,符合三角形的三边关系;②当AB+AD=9,BC+CD=18时,解得此时△ABC三边长分别为6,6,15,不符合三角形的三边关系,舍去.
综上,等腰△ABC的底边长为3.
7.解析 ∠B=2∠C.
证明:如图,在AC上截取AE=AB,连接DE,∵AD是△ABC的角平分线,∴∠BAD=∠EAD,∵AB=AE,AD=AD,∴△ABD≌△AED(SAS),
∴BD=ED,∠B=∠AED,
∵AC=AB+BD,AC=AE+CE,∴BD=CE.
∴DE=CE,∴∠C=∠EDC,
∴∠AED=∠EDC+∠C=2∠C.
∴∠B=2∠C.
8.C ∵△ABC是等边三角形,∴∠ACB=60°.∵CD=CE,∴∠E=∠CDE.∵∠ACB=∠E+∠CDE=2∠E=60°,∴∠E=30°.
9.D ∵△ABC为等边三角形,∴∠BAC=60°,
∵AD是等边△ABC的中线,
∴AD⊥BC,∠CAD=∠BAC=30°,
∵AE=AD,∴∠ADE=∠AED,
∵∠ADE+∠AED+∠CAD=180°,
∴∠ADE+∠ADE+30°=180°,
∴∠ADE=75°,∴∠EDC=90°-75°=15°.
10.4
解析 ∵△ABC为等边三角形,AB=8,∴BC=8.
∵AD为△ABC的角平分线,∴BD=CD,∴CD=4.
11.120
解析 ∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵BD,CE是等边三角形ABC的中线,
∴BD平分∠ABC,CE平分∠ACB,
∴∠FBC=∠ABC=30°,∠FCB=∠ACB=30°,
∴∠BFC=180°-∠FBC-∠FCB=120°.
12.证明 (1)∵△ABD、△BCE为等边三角形,
∴AB=DB,∠ABD=∠CBE=60°,BE=BC,
∴∠ABE=∠DBC,∠DBE=60°.
在△ABE和△DBC中,
∴△ABE≌△DBC(SAS).
(2)由(1)知△ABE≌△DBC,∴AE=DC.
(3)由(1)知△ABE≌△DBC,∴∠BAE=∠BDC.
∵∠DGH=∠AGB,∠DHA=180°-∠BDC-∠DGH,∠DBA=180°-∠BAE-∠AGB,
∴∠DHA=∠DBA=60°,
∴AE与DC所夹的锐角为60°.
(4)由(1)知△ABE≌△DBC,∴∠BAG=∠BDF.
在△ABG和△DBF中,
∴△ABG≌△DBF(ASA).
(5)由(4)知△ABG≌△DBF,∴BG=BF.
∴∠GFB=∠FGB,又∵∠GBF=60°,
∴∠GFB==60°,
∴∠GFB=∠FBC,∴GF∥AC.
13.B 如图:
网格中满足条件的点C的个数为6,故选B.
14.△ABD,△BCD,△ABC,△ACF,△ABF
解析 ∵AB=AC,∠BAC=36°,
∴∠ABC=∠ACB=72°,△ABC是等腰三角形,
∵BD是∠ABC的平分线,
∴∠ABD=∠CBD=36°=∠BAC,
∴AD=BD,∠BDC=∠BAC+∠ABD=72°=∠ACB,
∴△ABD是等腰三角形,BD=BC,
∴△BDC是等腰三角形,
∵AD=BD,E是AB的中点,
∴DE⊥AB,∴∠FEA=∠FEB=90°,
∵AE=BE,EF=EF,∴△AEF≌△BEF(SAS),
∴AF=BF,∠FAB=∠FBA=72°,
∴△ABF是等腰三角形,∠AFB=180°-72°-72°=36°,∠FAC=72°-36°=36°,∴∠AFB=∠FAC,
∴AC=CF,
∴△ACF是等腰三角形.
15.证明 (1)∵AB=AC,∴∠ABC=∠C,
∵MN∥BC,
∴∠AMN=∠ABC,∠ANM=∠C,
∴∠AMN=∠ANM,∴AM=AN,
∴△AMN是等腰三角形.
(2)∵BP平分∠ABC,∴∠MBP=∠CBP,
∵MN∥BC,∴∠MPB=∠CBP,
∴∠MBP=∠MPB,∴MB=MP,
∴△BPM是等腰三角形.
16.50 cm
解析 ∵∠DOC=60°,∴∠AOB=60°.∵OA=OB,∴△OAB是等边三角形,∴AB=OA=OB=50 cm.
17.证明 (1)∵BF=AC,AB=AE,∴FA=EC.
∵△DEF是等边三角形,∴EF=DE.
∵AE=CD,∴△AEF≌△CDE(SSS).
(2)由(1)知△AEF≌△CDE,∴∠FEA=∠EDC,
∵△DEF是等边三角形,∴∠DEF=60°.
∵∠BCA=∠EDC+∠DEC=∠FEA+∠DEC=∠DEF,
∴∠BCA=60°,同理可得∠BAC=60°,∴∠ABC=60°,
∴△ABC是等边三角形.
能力提升全练
18.C 根据平行线的性质可得∠DCA+∠CAB=180°,即∠DCE+∠ECA+∠EAC+∠EAB=180°,由△ACE为等边三角形得∠ECA=∠EAC=60°,所以∠EAB=180°-40°-60°-60°=20°.故选C.
19.D A.由“三个角都相等的三角形是等边三角形”可以判定△ABC是等边三角形,故本选项不符合题意.B.由“有一个角是60°的等腰三角形是等边三角形”可以判定△ABC是等边三角形,故本选项不符合题意.C.由“∠A=60°,∠B=60°”可以得到“∠A=∠B=∠C=60°”,则由“三个角都相等的三角形是等边三角形”可以判定△ABC是等边三角形,故本选项不符合题意.D.由“AB=AC且∠B=∠C”只能判定△ABC是等腰三角形,故本选项符合题意.故选D.
20.C ①当AB为等腰△ABC的底边时,符合条件的C点有4个;
②当AB为等腰△ABC的一个腰时,符合条件的C点有4个.
综上,符合条件的点C有8个.
21.6
解析 ∵等边三角形纸片ABC的边长为6,E,F是边BC上的三等分点,∴EF=2,
∵△ABC是等边三角形,∴∠B=∠C=60°,
∵DE∥AB,DF∥AC,
∴∠DEF=∠B=60°,∠DFE=∠C=60°,
∴∠D=∠DEF=∠DFE=60°,
∴△DEF是等边三角形,
∴DE=DF=EF=2,
∴剪下的△DEF的周长是2×3=6.
22.55°或125°
解析 分两种情况讨论:
①当一腰上的高在三角形内部时,如图1,
∵BD⊥AC,∴∠ADB=90°.
∵∠ABD=35°,∴∠A=180°-35°-90°=55°.
图1
②当一腰上的高在三角形外部时,如图2,
图2
∵BD⊥AC,∴∠BDC=90°.
∵∠ABD=35°,∴∠BAC=90°+35°=125°.
综上所述,这个等腰三角形顶角的度数为55°或125°.
23.36
解析 设等腰三角形顶角的度数为α,则底角度数为90°-α,由题意得α=,解得α=36°.
24.36°或45°
解析 分两种情况讨论:
(1)如图1,△ABC中,AB=AC,AD=BD=CD,
∴∠B=∠C=∠DAC=∠DAB,
∴∠BAC=2∠B,
∵∠BAC+∠B+∠C=180°,
∴4∠B=180°,∴∠B=45°.
(2)如图2,△ABC中,AB=AC,BD=AD,AC=CD,
∴∠B=∠C=∠BAD,∠CDA=∠CAD,
∴∠CAD=∠CDA=∠ABC+∠BAD=2∠B,
∴∠BAC=3∠B,
∵∠BAC+∠B+∠C=180°,
∴5∠B=180°,∴∠B=36°.
综上,原等腰三角形底角的度数为36°或45°.
图1 图2
25.解析 (1)证明:∵AF平分∠DAC,∴∠DAF=∠CAF,∵AF∥BC,∴∠DAF=∠B,∠CAF=∠ACB,
∴∠B=∠ACB,∴AB=AC,∴△ABC是等腰三角形.
(2)由(1)知∠B=∠ACB,
∵∠B=40°,∴∠ACB=∠B=40°,∴∠BAC=100°,
∴∠ACE=∠BAC+∠B=140°,∵CG平分∠ACE,
∴∠ECG=∠ACE=70°,∵AF∥BC,∴∠AGC=∠ECG=70°.
26.证明 如图,分别延长AE,BC交于点F,
∵AD∥BC,∴∠DAE=∠CFE,
∵点E是DC的中点,∴ED=CE,
在△ADE与△FCE中,
∴△ADE≌△FCE(AAS),
∴AD=CF,
∵AE平分∠BAD,∴∠DAF=∠BAF,
∵∠DAF=∠F,∴∠BAF=∠F,∴AB=BF,
∴AB=BF=BC+CF=BC+AD.
27.解析 (1)∵∠ABC=80°,BD=BC,
∴∠BDC=∠BCD=×(180°-80°)=50°,
∵∠A+∠ABC+∠ACB=180°,∠A=40°,
∴∠ACB=180°-40°-80°=60°,
∵CE=BC,∴△BCE是等边三角形,
∴∠EBC=60°,
∴∠ABE=∠ABC-∠EBC=80°-60°=20°.
(2)∠BEC+∠BDC=110°,
理由:设∠BEC=α,∠BDC=β,
则α=∠A+∠ABE=40°+∠ABE,
∴∠ABE=α-40°,
∵CE=BC,∴∠CBE=∠BEC=α,
∴∠CBD=α+α-40°=2α-40°,
∵BD=BC,∴∠BCD=∠BDC=β,
在△BCD中,∠CBD+∠BDC+∠BCD=180°,
∴2α-40°+β+β=180°,∴α+β=110°,
∴∠BEC+∠BDC=110°.
28.解析 (1)∠DAC的度数不会改变.理由:
∵EA=EC,∴∠EAC=∠C,
∵BA=BD,∴∠BAD=∠BDA,
∵∠BAE=90°,
∴∠B=90°-∠AED=90°-2∠C,
∴∠BAD=(180°-∠B)=[180°-(90°-2∠C)]=45°+∠C,
∴∠DAE=90°-∠BAD=90°-(45°+∠C)=45°-∠C,
∵∠EAC=∠C,
∴∠DAC=∠DAE+∠CAE=45°-∠C+∠C=45°.
(2)设∠ABC=m°,
∵AB=DB,∴∠BAD=(180°-m°)=90°-m°,
∵∠BAE=n°,∴∠AEB=180°-n°-m°,
∴∠DAE=n°-∠BAD=n°-90°+m°,
∵EA=EC,∴∠CAE=∠AEB=90°-n°-m°,
∴∠DAC=∠DAE+∠CAE=n°-90°+m°+90°-n°-m°=n°.
素养探究全练
29.解析 (1)图中等腰三角形为△AEF、△OEB、△OFC、△OBC、△ABC.
EF、BE、FC之间的数量关系是EF=BE+CF.
理由:∵BO、CO分别平分∠ABC、∠ACB,
∴∠ABO=∠OBC,∠ACO=∠OCB,
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCB,
∴∠EOB=∠EBO,∠FOC=∠FCO,
∴EO=EB,FO=FC,
∴EF=EO+OF=BE+CF.
(2)图中等腰三角形是△EOB、△FOC,(1)中的EF、BE、CF之间的数量关系仍然成立.
理由:∵BO、CO分别平分∠ABC、∠ACB,
∴∠ABO=∠OBC,∠ACO=∠OCB,
∵EF∥BC,∴∠EOB=∠OBC,∠FOC=∠OCB,
∴∠EOB=∠EBO,∠FOC=∠FCO,
∴EO=EB,FO=FC,
∴EF=EO+OF=BE+CF.
(3)图中等腰三角形是△EOB和△FOC,EF=BE-FC.理由:同(1)可证得EO=EB,
∵EO∥BC,∴∠FOC=∠OCG,
∵CO平分∠ACG,
∴∠ACO=∠OCG,∴∠FOC=∠FCO,∴FO=FC,
∴EF=EO-FO=BE-FC.
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
