2021-2022学年陕西省各地人教版数学九年级上册24.1 圆的有关性质 期末试题分类选编 (含解析)
文档属性
| 名称 | 2021-2022学年陕西省各地人教版数学九年级上册24.1 圆的有关性质 期末试题分类选编 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 799.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-25 07:06:02 | ||
图片预览




文档简介
24.1 圆的有关性质
1.(2022·陕西渭南·九年级期末)如图,半径为3的⊙O内有一点A,OA=,点P在⊙O上,当∠OPA最大时,S△OPA等于( )
A. B. C. D.1
2.(2022·陕西渭南·九年级期末)如图,的直径弦于点,若,,则的长为( )
A. B.12 C.10 D.5
3.(2022·陕西·紫阳县师训教研中心九年级期末)如图,在⊙O中,AB是弦,半径于点D,若OC=10,AB=16,则CD的长为( )
A.6 B.5 C.4 D.3
4.(2022·陕西·西安高新第一中学初中校区九年级期末)如图,已知⊙O的半径等于2cm,AB是直径,C,D是⊙O上的两点,且,则四边形ABCD的周长等于( )
A.8cm B.10cm C.12cm D.16cm
5.(2022·陕西·西北工业大学附属中学九年级期末)如图,BC是的直径,A,D是上的两点,连接AB,AD,BD,若,则的度数是( )
A. B. C. D.
6.(2022·陕西安康·九年级期末)如图,点A,B,C都在⊙O上,若∠C=35°,则∠AOB的度数为( )
A.35° B.55° C.145° D.70°
7.(2022·陕西·西安铁一中分校九年级期末)知图,AB为⊙O的直径,C、D为⊙O上两点,连接AC、CD,CD与AB相交于点E,若=2,∠C=20°,则∠AED的度数为( )
A.50° B.53° C.55° D.58°
8.(2022·陕西渭南·九年级期末)下列说法:①等弧所对的圆心角相等;②经过三点可以作一个圆;③平分弦的直径垂直于这条弦;④圆的内接平行四边形是矩形.其中正确的有( )
A.①② B.②③ C.③④ D.①④
9.(2022·陕西·紫阳县师训教研中心九年级期末)如图,四边形ABCD内接于⊙O,若,则∠BCD的度数是( )
A.50° B.80° C.100° D.130°
10.(2022·陕西安康·九年级期末)如图,四边形ABCD内接于,弦BD,若,则的大小为( )
A.62° B.56° C.52° D.50°
11.(2022·陕西·西安高新第一中学初中校区九年级期末)已知⊙O的直径CD=10,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8,则AC的长为________________.
12.(2022·陕西渭南·九年级期末)如图,把一个以点为圆心的圆的面积四等分,请用尺规作图画出一种分割方法.(不写作法,保留作图痕迹)
13.(2022·陕西·西安铁一中分校九年级期末)如图,点C为以AB为直径的圆外一点,请用尺规作图法作一条直线l,使得直线过点C,且将圆的周长分成相等的两部分(尺规作图,保留作图痕迹,不写作法)
14.(2022·陕西渭南·九年级期末)如图,在中,作出劣弧的中点D.(要求:尺规作图,保留作图痕迹,不写作法)
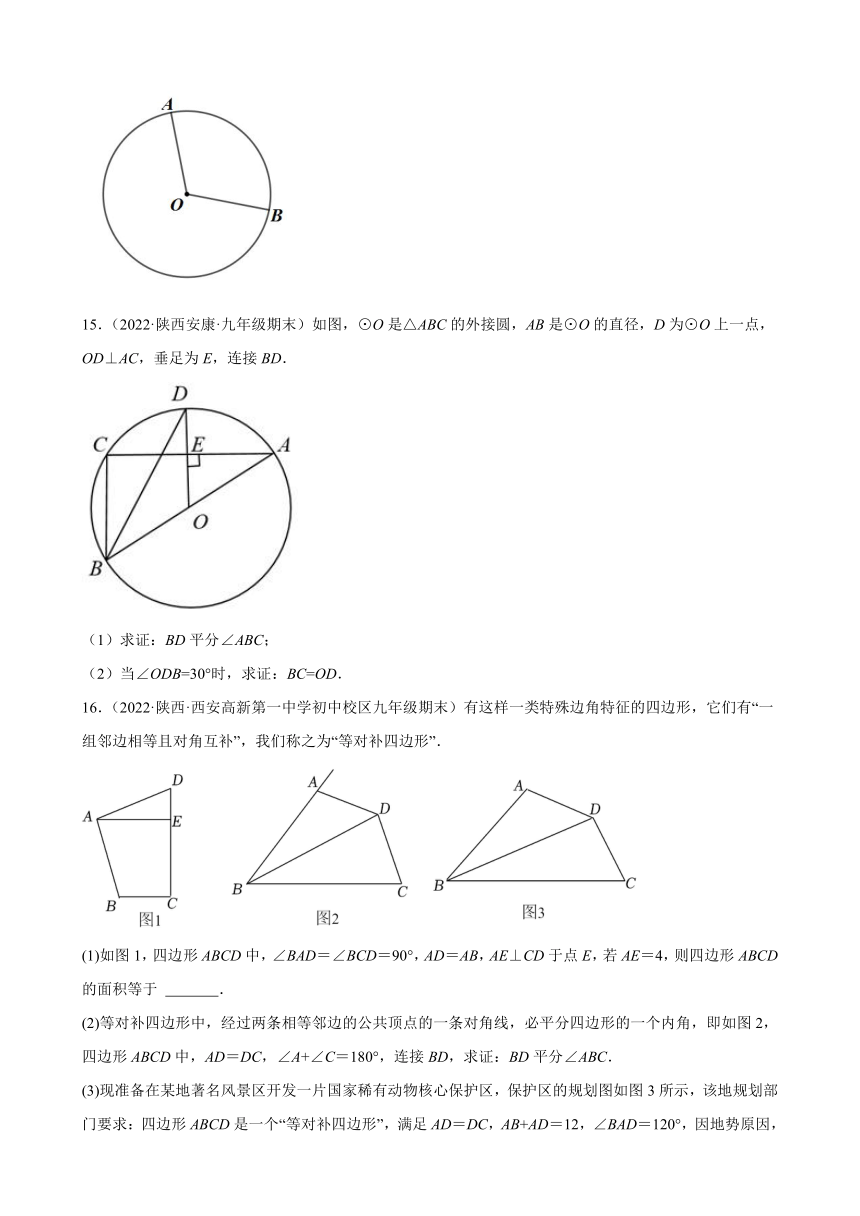
15.(2022·陕西安康·九年级期末)如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.
16.(2022·陕西·西安高新第一中学初中校区九年级期末)有这样一类特殊边角特征的四边形,它们有“一组邻边相等且对角互补”,我们称之为“等对补四边形”.
(1)如图1,四边形ABCD中,∠BAD=∠BCD=90°,AD=AB,AE⊥CD于点E,若AE=4,则四边形ABCD的面积等于 .
(2)等对补四边形中,经过两条相等邻边的公共顶点的一条对角线,必平分四边形的一个内角,即如图2,四边形ABCD中,AD=DC,∠A+∠C=180°,连接BD,求证:BD平分∠ABC.
(3)现准备在某地著名风景区开发一片国家稀有动物核心保护区,保护区的规划图如图3所示,该地规划部门要求:四边形ABCD是一个“等对补四边形”,满足AD=DC,AB+AD=12,∠BAD=120°,因地势原因,要求3≤AD≤6,求该区域四边形ABCD面积的最大值.
17.(2022·陕西·西安铁一中分校九年级期末)问题提出
(1)如图1,A、B为⊙O外的两点,请在⊙O上画出所有使得AC+BC的值最小的C点.
问题探究
(2)如图2,在四边形ABCD中,AB=AD=3,∠BCD=∠BAD=90°,AC=4,求BC+CD的值;
问题解决
(3)如图3,某城市要修建一块草坪,草坪由三条线段AB、BC、CD和圆弧AD周成,计划在圆弧AD段用花来布置成标志性造型,AB和CD段栽种观赏性树木,BC临湖.已知点E为BC上一点,BE=CE=6,长为4,且上任意一点F,满足∠BFE=30°,为了降低成本,现计划使得AB+CD最小,求AB+CD的最小值.
参考答案:
1.B
【解析】当时,取得最大值,在直角三角形中利用勾股定理求的值,再根据三角形的面积公式即可得出答案.
解:如图所示:、是定值,
时,最大,
在直角三角形中,,,
,
.
故选:B.
本题考查了解直角三角形.解答此题的关键是找出“当时,最大”这一隐含条件.
2.C
【解析】如图所示,连接OD,设,先用勾股定理求出,再在△OED中利用勾股定理求解即可.
解:如图所示,连接OD,
设,
∵AB⊥CD,CD=8,
∴CE=DE=4,∠BED=∠OED=90°,
∴,
∴,
∵,
∴,
解得,
∴AB=2r=10,
故选C.
本题主要考查了垂径定理和勾股定理,解题的关键在于能够熟练掌握垂径定理.
3.C
【解析】连接OA,如图,利用垂径定理得到AD=BD=AB=8,再利用勾股定理计算出OD,然后计算OC-OD即可.
解:连接OA,如图,
∵OC⊥AB,
∴AD=BD=AB=
在Rt△OAD中,OD=
∴CD=OC-OD=10-6=4.
故选C.
本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
4.B
【解析】连接OD、OC,根据圆心角、弧、弦间的关系证得△AOD是等边三角形,然后由可得=2cm,于是可以求出结果.
解:如图,连接OD、OC.
,
∠AOD=∠DOC=∠COB,;
∠AOD+∠DOC+∠COB=180°,
∠AOD=∠DOC=∠COB=60°;
OA=OD,
△AOD是等边三角形,⊙O的半径等于2cm,
AD=OD=OA=2cm;
,
AD=CD=BC=OA=2cm;
四边形ABCD的周长为:AD+CD+BC+AB=cm;
故选:B.
本题考查了心角、弧、弦间的关系与等边三角形的判定与性质.在同圆中,等弧所对的圆心角相等.
5.A
【解析】连接AC,如图,根据圆周角定理得到,,然后利用互余计算的度数.
连接AC,如图,
∵BC是的直径,
∴,
∵,
∴.
故答案为.
故选A.
本题考查圆周角定理和推论,解题的关键是掌握圆周角定理和推论.
6.D
∵∠C=35°,
∴∠AOB=2∠C=70°.
故选D.
7.C
【解析】连接OD,OC,先利用圆周角定理求出∠AOD,从而求出∠DOB,再根据=2,求出∠BOC,进而求出∠CAO,最后利用三角形的外角进行计算即可解答.
解:连接OD,OC,
∵∠ACD=20°,
∴∠AOD=2∠ACD=40°,
∴∠DOB=180°-∠AOD=140°,
∵=2,
∴∠BOD=2∠BOC,
∴∠BOC=70°,
∴∠CAO=∠BOC=35°,
∴∠AED=∠ACD+∠CAO=55°,
故选:C.
本题考查了圆周角定理,圆心角、弧、弦的关系、三角形外角的性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
8.D
【解析】根据圆的有关概念及性质,对选项逐个判断即可.
①等弧是能够完全重合的弧,因此等弧所对的圆心角相等,正确;
②经过不在同一直线上的三点可以作一个圆,故原命题错误;
③平分弦(不是直径)的直径垂直于这条弦,故原命题错误;
④圆的内接平行四边形是矩形,正确;
正确的有①④,
故答案为:D.
此题考查了圆的有关概念及性质,解题的关键是熟练掌握圆的相关概念以及性质.
9.D
【解析】根据圆周角定理求出∠A的度数,根据圆内接四边形的性质得出∠A+∠BCD=180°即可解答.
解:∵弧BCD对的圆周角是∠A,圆心角是∠BOD=100°,
∴∠A=∠BOD=50°,
∵A、B、C、D四点共圆,
∴∠A+∠BCD=180°,
∴∠BCD=130°.
故选:D.
本题主要考查了圆周角定理、圆内接四边形的性质等知识点,根据圆周角定理求得∠A的度数和得出∠A+∠BCD=180°是解答本题的关键.
10.B
【解析】由垂径定理,即;由等腰三角形的性质可得,即,最后根据圆的内接四边形对角互补即可解答.
解:∵,
∴,
∴,
∵,
∴,
∴,
∵四边形ABCD为的内接四边形,
∴.
故选:B.
本题主要考查了垂径定理、圆的内接四边形等知识点,掌握圆的内接四边形对角互补是解答本题的关键.
11.或
【解析】连结OA,由AB⊥CD,根据垂径定理得到AM=4,再根据勾股定理计算出OM=3,然后分类讨论:当如图1时,CM=8;当如图2时,CM=2,再利用勾股定理分别计算即可.
解:连结OA,
∵AB⊥CD,
∴AM=BM=AB=×8=4,
在Rt△OAM中,OA=5,
∴OM==3,
当如图1时,CM=OC+OM=5+3=8,
在Rt△ACM中,AC==;
当如图2时,CM=OC-OM=5-3=2,
在Rt△ACM中,AC==.
故答案为:或.
本题考查垂径定理,根据题意作出辅助线,构造出直角三角形是解题的关键.
12.见解析
【解析】由题意先过圆心作直径MN,进而作直径MN的垂直平分线EF即可.
解:如图,直线,直线即为所求.
本题考查圆以及垂直平分线的性质,熟练掌握垂直平分线的作图方法是解题的关键.
13.见解析
【解析】先作AB的垂直平分线得到AB的中点,然后连接OC得到直线l.
解:如图,直线l为所作.
本题考查了作图-复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
14.见解析
【解析】连接AB,作AB的垂直平分线即可得到劣弧AB的中点D.
解:如图所示:
连接AB,分别以A、B为圆心,以大于AB长的一半为半径画弧,两弧交于M点,连接OM交圆于点D,即为所求.
本题主要考查了线段的垂直平分线的性质,圆心角、弧、弦之间的关系,解题的关键在于能够熟练掌握相关知识进行求解.
15.(1)证明见解析;(2)证明见解析.
【解析】(1)由OD⊥AC OD为半径,根据垂径定理,即可得,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可证得BD平分∠ABC;
(2)首先由OB=OD,易求得∠AOD的度数,又由OD⊥AC于E,可求得∠A的度数,然后由AB是⊙O的直径,根据圆周角定理,可得∠ACB=90°,继而可证得BC=OD.
(1)∵OD⊥AC OD为半径,
∴,
∴∠CBD=∠ABD,
∴BD平分∠ABC;
(2)∵OB=OD,
∴∠OBD=∠0DB=30°,
∴∠AOD=∠OBD+∠ODB=30°+30°=60°,
又∵OD⊥AC于E,
∴∠OEA=90°,
∴∠A=180°﹣∠OEA﹣∠AOD=180°﹣90°﹣60°=30°,
又∵AB为⊙O的直径,
∴∠ACB=90°,在Rt△ACB中,BC=AB,
∵OD=AB,
∴BC=OD.
16.(1)9
(2)见解析
(3)
【解析】(1)过作,交的延长线于,求出四边形是矩形,根据矩形的性质得出,求出,根据得出,根据全等得出,,求出,求出,代入求出即可;
(2)如图1中,连接,.证明,,,四点共圆,利用圆周角定理即可解决问题.
(3)如图3中,延长到,使得,连接,过点作于,根点作于,于.设.构建二次函数,利用二次函数的性质即可解决问题.
(1)
解:如图1,过作,交的延长线于,
,
,
四边形是矩形,
,
,
,
在和中,
,
,
,,
四边形是矩形,
四边形是正方形,
,
.
故答案为:16;
(2)
解:证明:如图2中,连接.
,
,,,四点共圆,
,
,
,
平分.
(3)
解:如图3中,延长到,使得,连接,过点作于,过点作于,于.设.
,,
,
,
,
是等边三角形,
,
,
由(2)可知.平分,
,
,
,
,,
,,
,
,
,,
,
∵,
∴
∴时,有最大值,最大值.
本题属于四边形综合题,考查了“邻等对补四边形”的定义,解直角三角形,等边三角形的判定和性质,四点共圆,二次函数的应用等知识,解题的关键是理解题意,灵活运用所学知识解决问题,学会利用参数构建二次函数,利用二次函数的性质解决最值问题,属于中考压轴题.
17.(1)见解析
(2)
(3)
【解析】(1)利用两点之间线段最短求解;
(2)利用AAS证明,推出,,进而得出,再证四边形ANCM是正方形,结合AC=4,利用勾股定理求出正方形ANCM的边长,即可求解;
(3)如图(见解析)作辅助线,找出点F所在圆的圆心,证明,推出,进而得出,从而将AB与CD转化为一个三角形的两个边,依靠三角形的三边关系进行求解.
(1)
解:如图所示,连接AB,AB与⊙O的交点和 为所求C点;
(2)
解:如图,作于点M,作交BC的延长线于点N,
则,
又∵,
∴四边形ANCM是矩形,
∴,,
∴,
即,
在和中,
,
∴,
∴,,
∴,
∵四边形ANCM是矩形,,
∴四边形ANCM是正方形,
∴,
∴,
即,
∴,
∴;
(3)
解:∵点F在运动的过程中,满足,
∴点F可看作是在以BE为弦的圆上运动,为弦BE所对的圆周角,
∴弦BE所对的圆心角为:,
以BE为边向上作等边三角形BEO,可得点O为动点F所在圆的圆心,圆O的半径为6.
连接OA,OD,延长EO与圆O交于点G,连接GD.
∵长为4,半径,
∴,
又由等边三角形的性质知,
∴,
又∵,
∴,
又∵,
∴,
∴,
∴,
∴当G,D,C三点共线时,取最小值,取最小值,最小值为GC.
连接GB,如下图所示:
此时,G点与D点重合,A点与B点重合,
∵GE是直径,
∴,
在中,, ,
∴,
∴中,,
∴的最小值为.
本题考查全等三角形的判定与性质,正方形的判定与性质,圆周角定理的应用,等边三角形的性质,勾股定理解直角三角形等知识点,综合性很强,属于压轴题,第三问难度很大,将转化为,得出的最小值为GC是解题的关键.
1.(2022·陕西渭南·九年级期末)如图,半径为3的⊙O内有一点A,OA=,点P在⊙O上,当∠OPA最大时,S△OPA等于( )
A. B. C. D.1
2.(2022·陕西渭南·九年级期末)如图,的直径弦于点,若,,则的长为( )
A. B.12 C.10 D.5
3.(2022·陕西·紫阳县师训教研中心九年级期末)如图,在⊙O中,AB是弦,半径于点D,若OC=10,AB=16,则CD的长为( )
A.6 B.5 C.4 D.3
4.(2022·陕西·西安高新第一中学初中校区九年级期末)如图,已知⊙O的半径等于2cm,AB是直径,C,D是⊙O上的两点,且,则四边形ABCD的周长等于( )
A.8cm B.10cm C.12cm D.16cm
5.(2022·陕西·西北工业大学附属中学九年级期末)如图,BC是的直径,A,D是上的两点,连接AB,AD,BD,若,则的度数是( )
A. B. C. D.
6.(2022·陕西安康·九年级期末)如图,点A,B,C都在⊙O上,若∠C=35°,则∠AOB的度数为( )
A.35° B.55° C.145° D.70°
7.(2022·陕西·西安铁一中分校九年级期末)知图,AB为⊙O的直径,C、D为⊙O上两点,连接AC、CD,CD与AB相交于点E,若=2,∠C=20°,则∠AED的度数为( )
A.50° B.53° C.55° D.58°
8.(2022·陕西渭南·九年级期末)下列说法:①等弧所对的圆心角相等;②经过三点可以作一个圆;③平分弦的直径垂直于这条弦;④圆的内接平行四边形是矩形.其中正确的有( )
A.①② B.②③ C.③④ D.①④
9.(2022·陕西·紫阳县师训教研中心九年级期末)如图,四边形ABCD内接于⊙O,若,则∠BCD的度数是( )
A.50° B.80° C.100° D.130°
10.(2022·陕西安康·九年级期末)如图,四边形ABCD内接于,弦BD,若,则的大小为( )
A.62° B.56° C.52° D.50°
11.(2022·陕西·西安高新第一中学初中校区九年级期末)已知⊙O的直径CD=10,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8,则AC的长为________________.
12.(2022·陕西渭南·九年级期末)如图,把一个以点为圆心的圆的面积四等分,请用尺规作图画出一种分割方法.(不写作法,保留作图痕迹)
13.(2022·陕西·西安铁一中分校九年级期末)如图,点C为以AB为直径的圆外一点,请用尺规作图法作一条直线l,使得直线过点C,且将圆的周长分成相等的两部分(尺规作图,保留作图痕迹,不写作法)
14.(2022·陕西渭南·九年级期末)如图,在中,作出劣弧的中点D.(要求:尺规作图,保留作图痕迹,不写作法)
15.(2022·陕西安康·九年级期末)如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.
16.(2022·陕西·西安高新第一中学初中校区九年级期末)有这样一类特殊边角特征的四边形,它们有“一组邻边相等且对角互补”,我们称之为“等对补四边形”.
(1)如图1,四边形ABCD中,∠BAD=∠BCD=90°,AD=AB,AE⊥CD于点E,若AE=4,则四边形ABCD的面积等于 .
(2)等对补四边形中,经过两条相等邻边的公共顶点的一条对角线,必平分四边形的一个内角,即如图2,四边形ABCD中,AD=DC,∠A+∠C=180°,连接BD,求证:BD平分∠ABC.
(3)现准备在某地著名风景区开发一片国家稀有动物核心保护区,保护区的规划图如图3所示,该地规划部门要求:四边形ABCD是一个“等对补四边形”,满足AD=DC,AB+AD=12,∠BAD=120°,因地势原因,要求3≤AD≤6,求该区域四边形ABCD面积的最大值.
17.(2022·陕西·西安铁一中分校九年级期末)问题提出
(1)如图1,A、B为⊙O外的两点,请在⊙O上画出所有使得AC+BC的值最小的C点.
问题探究
(2)如图2,在四边形ABCD中,AB=AD=3,∠BCD=∠BAD=90°,AC=4,求BC+CD的值;
问题解决
(3)如图3,某城市要修建一块草坪,草坪由三条线段AB、BC、CD和圆弧AD周成,计划在圆弧AD段用花来布置成标志性造型,AB和CD段栽种观赏性树木,BC临湖.已知点E为BC上一点,BE=CE=6,长为4,且上任意一点F,满足∠BFE=30°,为了降低成本,现计划使得AB+CD最小,求AB+CD的最小值.
参考答案:
1.B
【解析】当时,取得最大值,在直角三角形中利用勾股定理求的值,再根据三角形的面积公式即可得出答案.
解:如图所示:、是定值,
时,最大,
在直角三角形中,,,
,
.
故选:B.
本题考查了解直角三角形.解答此题的关键是找出“当时,最大”这一隐含条件.
2.C
【解析】如图所示,连接OD,设,先用勾股定理求出,再在△OED中利用勾股定理求解即可.
解:如图所示,连接OD,
设,
∵AB⊥CD,CD=8,
∴CE=DE=4,∠BED=∠OED=90°,
∴,
∴,
∵,
∴,
解得,
∴AB=2r=10,
故选C.
本题主要考查了垂径定理和勾股定理,解题的关键在于能够熟练掌握垂径定理.
3.C
【解析】连接OA,如图,利用垂径定理得到AD=BD=AB=8,再利用勾股定理计算出OD,然后计算OC-OD即可.
解:连接OA,如图,
∵OC⊥AB,
∴AD=BD=AB=
在Rt△OAD中,OD=
∴CD=OC-OD=10-6=4.
故选C.
本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
4.B
【解析】连接OD、OC,根据圆心角、弧、弦间的关系证得△AOD是等边三角形,然后由可得=2cm,于是可以求出结果.
解:如图,连接OD、OC.
,
∠AOD=∠DOC=∠COB,;
∠AOD+∠DOC+∠COB=180°,
∠AOD=∠DOC=∠COB=60°;
OA=OD,
△AOD是等边三角形,⊙O的半径等于2cm,
AD=OD=OA=2cm;
,
AD=CD=BC=OA=2cm;
四边形ABCD的周长为:AD+CD+BC+AB=cm;
故选:B.
本题考查了心角、弧、弦间的关系与等边三角形的判定与性质.在同圆中,等弧所对的圆心角相等.
5.A
【解析】连接AC,如图,根据圆周角定理得到,,然后利用互余计算的度数.
连接AC,如图,
∵BC是的直径,
∴,
∵,
∴.
故答案为.
故选A.
本题考查圆周角定理和推论,解题的关键是掌握圆周角定理和推论.
6.D
∵∠C=35°,
∴∠AOB=2∠C=70°.
故选D.
7.C
【解析】连接OD,OC,先利用圆周角定理求出∠AOD,从而求出∠DOB,再根据=2,求出∠BOC,进而求出∠CAO,最后利用三角形的外角进行计算即可解答.
解:连接OD,OC,
∵∠ACD=20°,
∴∠AOD=2∠ACD=40°,
∴∠DOB=180°-∠AOD=140°,
∵=2,
∴∠BOD=2∠BOC,
∴∠BOC=70°,
∴∠CAO=∠BOC=35°,
∴∠AED=∠ACD+∠CAO=55°,
故选:C.
本题考查了圆周角定理,圆心角、弧、弦的关系、三角形外角的性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
8.D
【解析】根据圆的有关概念及性质,对选项逐个判断即可.
①等弧是能够完全重合的弧,因此等弧所对的圆心角相等,正确;
②经过不在同一直线上的三点可以作一个圆,故原命题错误;
③平分弦(不是直径)的直径垂直于这条弦,故原命题错误;
④圆的内接平行四边形是矩形,正确;
正确的有①④,
故答案为:D.
此题考查了圆的有关概念及性质,解题的关键是熟练掌握圆的相关概念以及性质.
9.D
【解析】根据圆周角定理求出∠A的度数,根据圆内接四边形的性质得出∠A+∠BCD=180°即可解答.
解:∵弧BCD对的圆周角是∠A,圆心角是∠BOD=100°,
∴∠A=∠BOD=50°,
∵A、B、C、D四点共圆,
∴∠A+∠BCD=180°,
∴∠BCD=130°.
故选:D.
本题主要考查了圆周角定理、圆内接四边形的性质等知识点,根据圆周角定理求得∠A的度数和得出∠A+∠BCD=180°是解答本题的关键.
10.B
【解析】由垂径定理,即;由等腰三角形的性质可得,即,最后根据圆的内接四边形对角互补即可解答.
解:∵,
∴,
∴,
∵,
∴,
∴,
∵四边形ABCD为的内接四边形,
∴.
故选:B.
本题主要考查了垂径定理、圆的内接四边形等知识点,掌握圆的内接四边形对角互补是解答本题的关键.
11.或
【解析】连结OA,由AB⊥CD,根据垂径定理得到AM=4,再根据勾股定理计算出OM=3,然后分类讨论:当如图1时,CM=8;当如图2时,CM=2,再利用勾股定理分别计算即可.
解:连结OA,
∵AB⊥CD,
∴AM=BM=AB=×8=4,
在Rt△OAM中,OA=5,
∴OM==3,
当如图1时,CM=OC+OM=5+3=8,
在Rt△ACM中,AC==;
当如图2时,CM=OC-OM=5-3=2,
在Rt△ACM中,AC==.
故答案为:或.
本题考查垂径定理,根据题意作出辅助线,构造出直角三角形是解题的关键.
12.见解析
【解析】由题意先过圆心作直径MN,进而作直径MN的垂直平分线EF即可.
解:如图,直线,直线即为所求.
本题考查圆以及垂直平分线的性质,熟练掌握垂直平分线的作图方法是解题的关键.
13.见解析
【解析】先作AB的垂直平分线得到AB的中点,然后连接OC得到直线l.
解:如图,直线l为所作.
本题考查了作图-复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
14.见解析
【解析】连接AB,作AB的垂直平分线即可得到劣弧AB的中点D.
解:如图所示:
连接AB,分别以A、B为圆心,以大于AB长的一半为半径画弧,两弧交于M点,连接OM交圆于点D,即为所求.
本题主要考查了线段的垂直平分线的性质,圆心角、弧、弦之间的关系,解题的关键在于能够熟练掌握相关知识进行求解.
15.(1)证明见解析;(2)证明见解析.
【解析】(1)由OD⊥AC OD为半径,根据垂径定理,即可得,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可证得BD平分∠ABC;
(2)首先由OB=OD,易求得∠AOD的度数,又由OD⊥AC于E,可求得∠A的度数,然后由AB是⊙O的直径,根据圆周角定理,可得∠ACB=90°,继而可证得BC=OD.
(1)∵OD⊥AC OD为半径,
∴,
∴∠CBD=∠ABD,
∴BD平分∠ABC;
(2)∵OB=OD,
∴∠OBD=∠0DB=30°,
∴∠AOD=∠OBD+∠ODB=30°+30°=60°,
又∵OD⊥AC于E,
∴∠OEA=90°,
∴∠A=180°﹣∠OEA﹣∠AOD=180°﹣90°﹣60°=30°,
又∵AB为⊙O的直径,
∴∠ACB=90°,在Rt△ACB中,BC=AB,
∵OD=AB,
∴BC=OD.
16.(1)9
(2)见解析
(3)
【解析】(1)过作,交的延长线于,求出四边形是矩形,根据矩形的性质得出,求出,根据得出,根据全等得出,,求出,求出,代入求出即可;
(2)如图1中,连接,.证明,,,四点共圆,利用圆周角定理即可解决问题.
(3)如图3中,延长到,使得,连接,过点作于,根点作于,于.设.构建二次函数,利用二次函数的性质即可解决问题.
(1)
解:如图1,过作,交的延长线于,
,
,
四边形是矩形,
,
,
,
在和中,
,
,
,,
四边形是矩形,
四边形是正方形,
,
.
故答案为:16;
(2)
解:证明:如图2中,连接.
,
,,,四点共圆,
,
,
,
平分.
(3)
解:如图3中,延长到,使得,连接,过点作于,过点作于,于.设.
,,
,
,
,
是等边三角形,
,
,
由(2)可知.平分,
,
,
,
,,
,,
,
,
,,
,
∵,
∴
∴时,有最大值,最大值.
本题属于四边形综合题,考查了“邻等对补四边形”的定义,解直角三角形,等边三角形的判定和性质,四点共圆,二次函数的应用等知识,解题的关键是理解题意,灵活运用所学知识解决问题,学会利用参数构建二次函数,利用二次函数的性质解决最值问题,属于中考压轴题.
17.(1)见解析
(2)
(3)
【解析】(1)利用两点之间线段最短求解;
(2)利用AAS证明,推出,,进而得出,再证四边形ANCM是正方形,结合AC=4,利用勾股定理求出正方形ANCM的边长,即可求解;
(3)如图(见解析)作辅助线,找出点F所在圆的圆心,证明,推出,进而得出,从而将AB与CD转化为一个三角形的两个边,依靠三角形的三边关系进行求解.
(1)
解:如图所示,连接AB,AB与⊙O的交点和 为所求C点;
(2)
解:如图,作于点M,作交BC的延长线于点N,
则,
又∵,
∴四边形ANCM是矩形,
∴,,
∴,
即,
在和中,
,
∴,
∴,,
∴,
∵四边形ANCM是矩形,,
∴四边形ANCM是正方形,
∴,
∴,
即,
∴,
∴;
(3)
解:∵点F在运动的过程中,满足,
∴点F可看作是在以BE为弦的圆上运动,为弦BE所对的圆周角,
∴弦BE所对的圆心角为:,
以BE为边向上作等边三角形BEO,可得点O为动点F所在圆的圆心,圆O的半径为6.
连接OA,OD,延长EO与圆O交于点G,连接GD.
∵长为4,半径,
∴,
又由等边三角形的性质知,
∴,
又∵,
∴,
又∵,
∴,
∴,
∴,
∴当G,D,C三点共线时,取最小值,取最小值,最小值为GC.
连接GB,如下图所示:
此时,G点与D点重合,A点与B点重合,
∵GE是直径,
∴,
在中,, ,
∴,
∴中,,
∴的最小值为.
本题考查全等三角形的判定与性质,正方形的判定与性质,圆周角定理的应用,等边三角形的性质,勾股定理解直角三角形等知识点,综合性很强,属于压轴题,第三问难度很大,将转化为,得出的最小值为GC是解题的关键.
同课章节目录
