2022-2023学年人教版数学七年级上册第四章 本章综合检测(含解析)
文档属性
| 名称 | 2022-2023学年人教版数学七年级上册第四章 本章综合检测(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 833.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-25 16:55:27 | ||
图片预览



文档简介
本章综合检测
(时间:60分钟 满分:100分)
一、选择题(每小题3分,共30分)
1.下面说法错误的是 ( )
A.圆柱的侧面展开图是长方形或正方形
B.圆锥除底面外,其余的面都是三角形
C.棱锥的侧面是三角形
D.正方体是四棱柱,也是六面体
2.下列说法中,正确的有 ( )
①两点之间,线段最短;②连接两点间的线段,叫做两点间的距离;③角的大小与角的两边的长短无关;④射线是直线的一部分,所以射线比直线短.
A.1个 B.2个 C.3个 D.4个
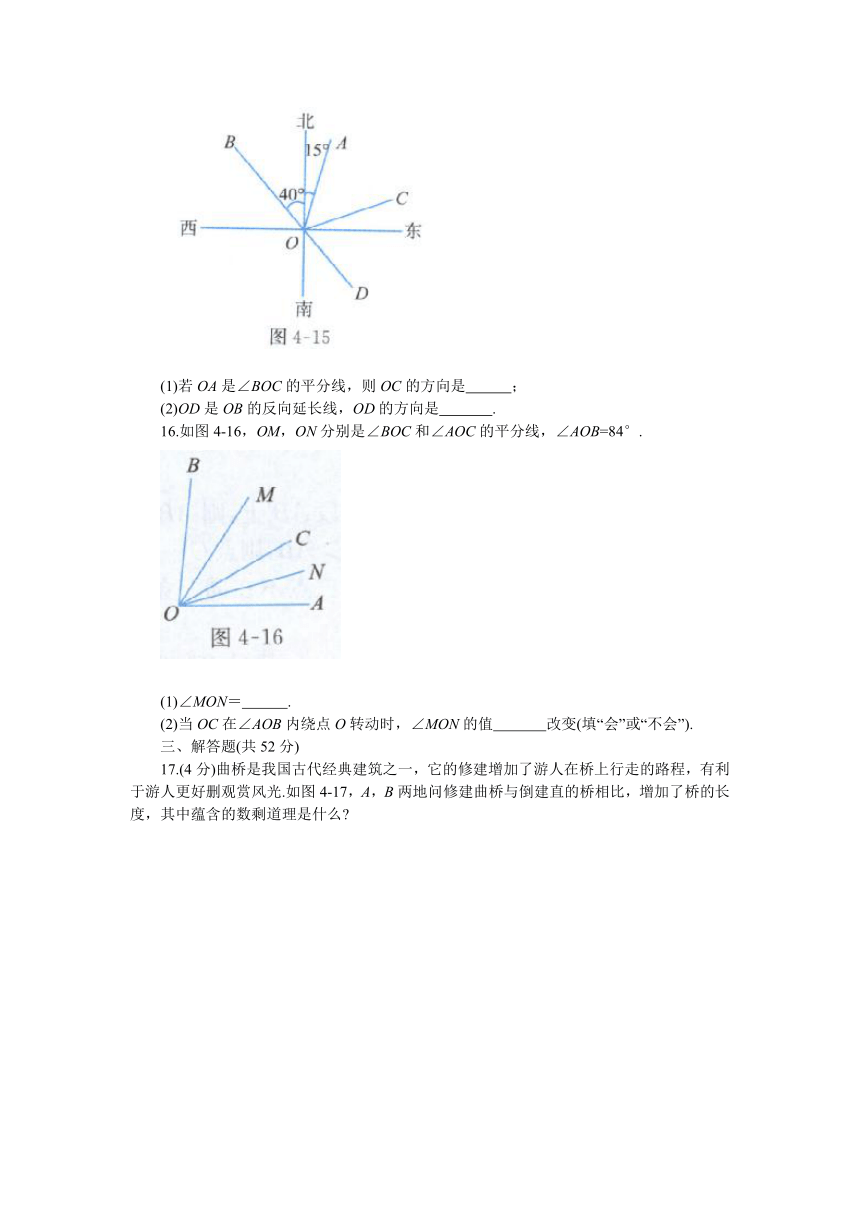
3.(湖南衡阳中考)下列不是三棱柱展开图的是 ( )
4.下面各角,可能与30°角互补的是 ( )
5.(山东济宁中考)如图4-1l,一个几何体上半部为正四棱锥,下半部为正方体,且有一个面涂有颜色.该几何体的表面展开图是 ( )
6.沿圆柱体上底面直径截去一部分后的物体如图4-12所示,从上向下看到的图形是 ( )
7.下列说法不正确的是 ( )
A.若点C在线段BA的延长线上,则BA=AC-BC
B.若点C在线段AB上,则AB=AC+BC
C.若AC+BC>AB,则点C一定在线段AB外
D.若A,B,C三点不在同一条直线上,则AB8.线段AB=12 cm,点C在线段AB上,且AC=BC,M为线段BC的中点,则线段AM的长为 ( )
A.4.5 cm B.6.5 cm C.7.5 cm D.8 cm
9.如图4-13所示,∠1=15°,∠AOC=90°,点B,O,D在同一条直线上,则么2的度数为 ( )
A.75° B.15° C.105° D.165°
10.将一副直角三角尺按如图4-14所示方式放置,若∠AOD=20°,则∠BOC的大小为 ( )
A.140° B.160° C.170° D.150°
二、填空题(每小题3分,共18分)
11.一个角的补角是36°35′,这个角是 .
12.已知C是线段AB的中点,AB=2,则BC= .
13.29.42°= (用度、分、秒的形式表示).
14.一节课40 min,钟表的时针转过的角度是 .
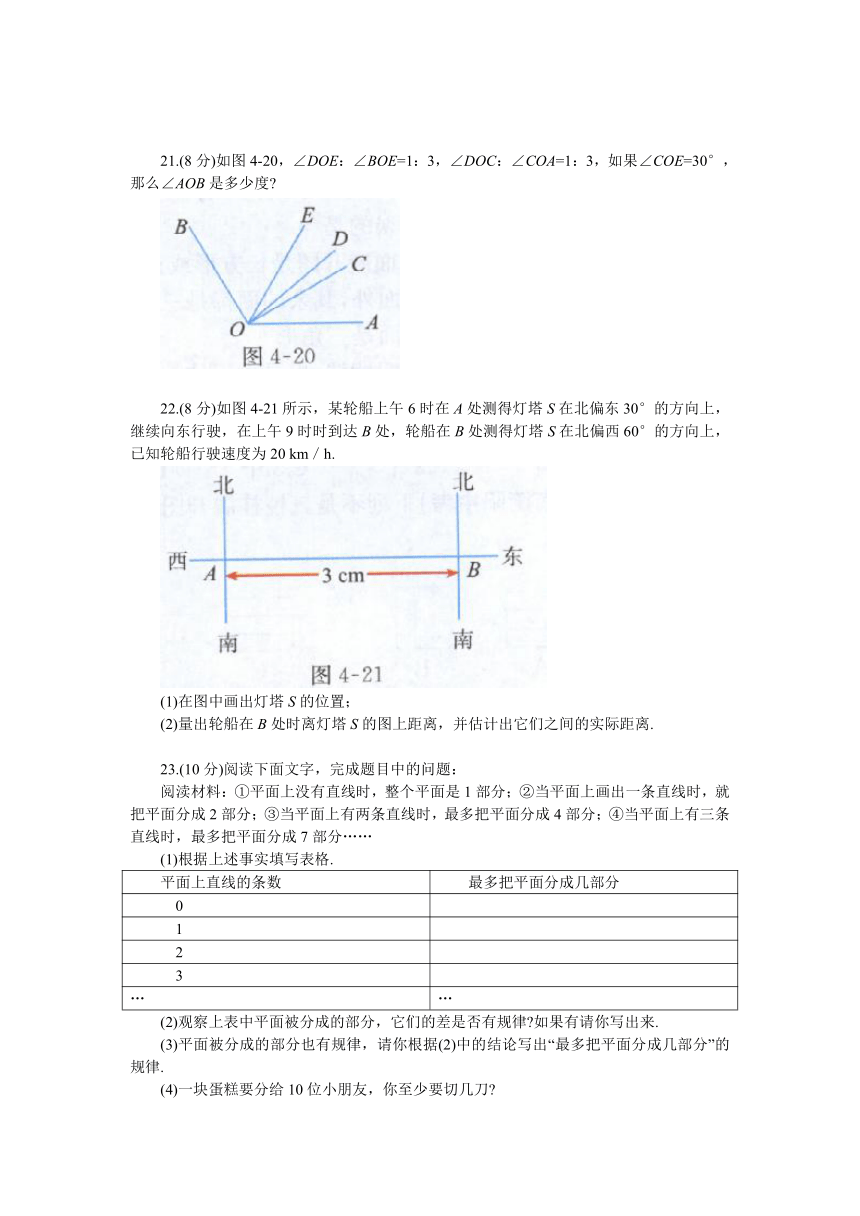
15.如图4-15,OA的方向是北偏东15°,OB的方向是北偏西40°.
(1)若OA是∠BOC的平分线,则OC的方向是 ;
(2)OD是OB的反向延长线,OD的方向是 .
16.如图4-16,OM,ON分别是∠BOC和∠AOC的平分线,∠AOB=84°.
(1)∠MON= .
(2)当OC在∠AOB内绕点O转动时,∠MON的值 改变(填“会”或“不会”).
三、解答题(共52分)
17.(4分)曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好删观赏风光.如图4-17,A,B两地问修建曲桥与倒建直的桥相比,增加了桥的长度,其中蕴含的数剩道理是什么
18.(8分)如图4-18所示,四点A,B,C,D(任意三点都不在同一条直线上),按照下列语句画出图形:
(1)画线段AB;
(2)画线段BD,延长线段BD;
(8)画线段AC,与线段BD相交于点O;
(4)画线段BC,并反向延长线段BC.
19.(6分)在一个仓库里堆放有若干个相同的正方体货箱,仓库管理员将从三个方向看到的这堆货箱的图形画出来,如图4-19所示,则这堆货箱共有多少个
20.(8分)已知:线段AB=15 cm,C为线段AB的中点,E为直线AB上的一点,D为线段AE的中点,且DE=6 cm,求线段CE的长.
21.(8分)如图4-20,∠DOE:∠BOE=1:3,∠DOC:∠COA=1:3,如果∠COE=30°,那么∠AOB是多少度
22.(8分)如图4-21所示,某轮船上午6时在A处测得灯塔S在北偏东30°的方向上,继续向东行驶,在上午9时时到达B处,轮船在B处测得灯塔S在北偏西60°的方向上,已知轮船行驶速度为20 km/h.
(1)在图中画出灯塔S的位置;
(2)量出轮船在B处时离灯塔S的图上距离,并估计出它们之间的实际距离.
23.(10分)阅读下面文字,完成题目中的问题:
阅渎材料:①平面上没有直线时,整个平面是1部分;②当平面上画出一条直线时,就把平面分成2部分;③当平面上有两条直线时,最多把平面分成4部分;④当平面上有三条直线时,最多把平面分成7部分……
(1)根据上述事实填写表格.
平面上直线的条数 最多把平面分成几部分
0
1
2
3
… …
(2)观察上表中平面被分成的部分,它们的差是否有规律 如果有请你写出来.
(3)平面被分成的部分也有规律,请你根据(2)中的结论写出“最多把平面分成几部分”的规律.
(4)一块蛋糕要分给10位小朋友,你至少要切几刀
参考答案
1.B 解析:圆锥的侧面是一个曲面,不是三角形.
2.B解析:①和③正确;②应为连接两点间的线段的长度,叫做两点间的距离;④射线与直线无法比较长短.
3.B 解析:A,C,D项中三个长方形能围成三棱柱的侧面,两个三角形围成三棱柱的上、下两底面,故均能围成三棱柱,均是三棱柱的表面展开图.B项围成三棱柱时,两个三角形重合为同一底面,没有另一底面,故B项不能围成三棱柱.故选B.
4.D 解析:30°角的补角是150°的角,是一个钝角,故选D.
5.B 解析:由题图中几何体可知,与涂有颜色的面相邻的必有一个三角形,所以选项A,C排除,而选项D中的图形无法折叠成题图中的几何体,故选B.
6.D 解析:从上向下看到的图形仍然是一个圆,只不过中间多了一条轮廓线,此轮廓线可以看到,因此为实线.
7.A 解析:若点C在线段BA的延长线上,则BA=BC-AC.
8.C 解析:因为AB=12 cm,AC=BC,
所以AC=AB=3 cm,
BC=AB=9 cm.
又因为M为线段BC的中点,
所以CM=BC=4.5 cm,
所以AM=AC+CM=3+4.5=7.5(cm).
9.C 解析:因为∠1=15°,∠AOC=90°,所以∠BOC=∠AOC-∠1=90°-15°=75°.
因为∠2+∠BOC=∠BOD=180°,
所以∠2=180°-75°=105°.
10.B 解析:因为∠AOD=20°,∠COD=∠AOB=90°,所以∠COA=90°-20°=70°,所以∠BOC=∠COA+∠AOB=70°+90°=160°.
11.143°25′ 解析:180°-36°35′=179°60′-36°35′=143°25′.
12.1 解析:根据线段中点的定义可得,BC=AB=1.
13.29°25′12″ 解析:29.42°=29°+0.42°
=29°+(0.42×60)′
=29°+25.2′
=29°+25′+0.2′
=29°+25′+(0.2×60)″
=29°+25′+12″
=29°25′12″.
14.20° 解析:经过40 min,钟表的时针转过个大格,所以钟表的时针转过的角度为×=20°.
15.(1)北偏东70° 解析:因为OA是∠BOC的平分线,所以∠AOC=∠AOB=40°+15°=55°. 因为15°+55°=70°,所以OC的方向是北偏东70°.
(2)南偏东40°
16.(1)42° (2)不会 解析:∠MON=∠MOC+∠NOC-∠BOC+∠AOC-(∠BOC+∠AOC)-∠AOB=×84°=42°.
17.解:其中蕴含的数学道理是两点之间,线段最短.
18.解:如答图4-1所示.
19.解:从正面看可知货箱共有2层,结合从上面看得到的图形可知,第一层有4个货箱,结合从左面看得到的图形可知,第2层有1个货箱,所以这堆货箱共有5个.
20.解:因为D为线段AE的中点,且DE=6 cm,所以AE=2DE=12 cm.
(1)当点E在点A的右边时,如答图4-2,
CE=AE-AC=AE-AB=12-×15=4.5(cm).
(2)当点E在点A的左边时,如答图4-3,
CE=AE+AC=AE+AB=12+×15=19.5(cm).
综上所述,CE的长度为4.5 cm或19.5 cm.
21.解:方法l:因为∠DOE:∠BOE=1:3,
∠DOC:∠COA=1:3,
所以么∠BOE=3∠DOE,∠COA=3∠DOC,
所以∠BOD-4∠DOE,∠AOD=4∠DOC,
所以∠AOB=∠BOD+∠AOD
=4∠DOE+4∠DOC
=4(∠DOE+∠DOC)
=4∠COE=120°.
方法2:设∠DOE=x,∠COD=y,
则∠BOE=3x,∠COA=3y.
因为∠AOB=∠DOE+∠COD+∠BOE+∠COA,
所以∠AOB=4x+4y=4(x+y).
因为∠COE=∠DOE+∠COD=x+y,
所以∠AOB=4(x+y)=4∠COE=120°.
22.解:(1)灯塔S的位置如答网4-4所示.
(2)因为轮船从A处以20 km/h的速度向东行驶3 h到达B处,
所以AB的实际长度为20×3=60(km).
因此,图上1 cm表示实际长度20 km.
又量得SB≈2.6 cm,因此SB的实际长度约为52 km.
23.解:(1)从上到下填写表格依次为1,2,4,7.
(2)有规律,相邻两数的差依次为1,2,3,4,….
(3)当有n条直线时,最多把平面分成(1+1+2+3+…+n)部分,即部分.
(4)4刀.
(时间:60分钟 满分:100分)
一、选择题(每小题3分,共30分)
1.下面说法错误的是 ( )
A.圆柱的侧面展开图是长方形或正方形
B.圆锥除底面外,其余的面都是三角形
C.棱锥的侧面是三角形
D.正方体是四棱柱,也是六面体
2.下列说法中,正确的有 ( )
①两点之间,线段最短;②连接两点间的线段,叫做两点间的距离;③角的大小与角的两边的长短无关;④射线是直线的一部分,所以射线比直线短.
A.1个 B.2个 C.3个 D.4个
3.(湖南衡阳中考)下列不是三棱柱展开图的是 ( )
4.下面各角,可能与30°角互补的是 ( )
5.(山东济宁中考)如图4-1l,一个几何体上半部为正四棱锥,下半部为正方体,且有一个面涂有颜色.该几何体的表面展开图是 ( )
6.沿圆柱体上底面直径截去一部分后的物体如图4-12所示,从上向下看到的图形是 ( )
7.下列说法不正确的是 ( )
A.若点C在线段BA的延长线上,则BA=AC-BC
B.若点C在线段AB上,则AB=AC+BC
C.若AC+BC>AB,则点C一定在线段AB外
D.若A,B,C三点不在同一条直线上,则AB
A.4.5 cm B.6.5 cm C.7.5 cm D.8 cm
9.如图4-13所示,∠1=15°,∠AOC=90°,点B,O,D在同一条直线上,则么2的度数为 ( )
A.75° B.15° C.105° D.165°
10.将一副直角三角尺按如图4-14所示方式放置,若∠AOD=20°,则∠BOC的大小为 ( )
A.140° B.160° C.170° D.150°
二、填空题(每小题3分,共18分)
11.一个角的补角是36°35′,这个角是 .
12.已知C是线段AB的中点,AB=2,则BC= .
13.29.42°= (用度、分、秒的形式表示).
14.一节课40 min,钟表的时针转过的角度是 .
15.如图4-15,OA的方向是北偏东15°,OB的方向是北偏西40°.
(1)若OA是∠BOC的平分线,则OC的方向是 ;
(2)OD是OB的反向延长线,OD的方向是 .
16.如图4-16,OM,ON分别是∠BOC和∠AOC的平分线,∠AOB=84°.
(1)∠MON= .
(2)当OC在∠AOB内绕点O转动时,∠MON的值 改变(填“会”或“不会”).
三、解答题(共52分)
17.(4分)曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好删观赏风光.如图4-17,A,B两地问修建曲桥与倒建直的桥相比,增加了桥的长度,其中蕴含的数剩道理是什么
18.(8分)如图4-18所示,四点A,B,C,D(任意三点都不在同一条直线上),按照下列语句画出图形:
(1)画线段AB;
(2)画线段BD,延长线段BD;
(8)画线段AC,与线段BD相交于点O;
(4)画线段BC,并反向延长线段BC.
19.(6分)在一个仓库里堆放有若干个相同的正方体货箱,仓库管理员将从三个方向看到的这堆货箱的图形画出来,如图4-19所示,则这堆货箱共有多少个
20.(8分)已知:线段AB=15 cm,C为线段AB的中点,E为直线AB上的一点,D为线段AE的中点,且DE=6 cm,求线段CE的长.
21.(8分)如图4-20,∠DOE:∠BOE=1:3,∠DOC:∠COA=1:3,如果∠COE=30°,那么∠AOB是多少度
22.(8分)如图4-21所示,某轮船上午6时在A处测得灯塔S在北偏东30°的方向上,继续向东行驶,在上午9时时到达B处,轮船在B处测得灯塔S在北偏西60°的方向上,已知轮船行驶速度为20 km/h.
(1)在图中画出灯塔S的位置;
(2)量出轮船在B处时离灯塔S的图上距离,并估计出它们之间的实际距离.
23.(10分)阅读下面文字,完成题目中的问题:
阅渎材料:①平面上没有直线时,整个平面是1部分;②当平面上画出一条直线时,就把平面分成2部分;③当平面上有两条直线时,最多把平面分成4部分;④当平面上有三条直线时,最多把平面分成7部分……
(1)根据上述事实填写表格.
平面上直线的条数 最多把平面分成几部分
0
1
2
3
… …
(2)观察上表中平面被分成的部分,它们的差是否有规律 如果有请你写出来.
(3)平面被分成的部分也有规律,请你根据(2)中的结论写出“最多把平面分成几部分”的规律.
(4)一块蛋糕要分给10位小朋友,你至少要切几刀
参考答案
1.B 解析:圆锥的侧面是一个曲面,不是三角形.
2.B解析:①和③正确;②应为连接两点间的线段的长度,叫做两点间的距离;④射线与直线无法比较长短.
3.B 解析:A,C,D项中三个长方形能围成三棱柱的侧面,两个三角形围成三棱柱的上、下两底面,故均能围成三棱柱,均是三棱柱的表面展开图.B项围成三棱柱时,两个三角形重合为同一底面,没有另一底面,故B项不能围成三棱柱.故选B.
4.D 解析:30°角的补角是150°的角,是一个钝角,故选D.
5.B 解析:由题图中几何体可知,与涂有颜色的面相邻的必有一个三角形,所以选项A,C排除,而选项D中的图形无法折叠成题图中的几何体,故选B.
6.D 解析:从上向下看到的图形仍然是一个圆,只不过中间多了一条轮廓线,此轮廓线可以看到,因此为实线.
7.A 解析:若点C在线段BA的延长线上,则BA=BC-AC.
8.C 解析:因为AB=12 cm,AC=BC,
所以AC=AB=3 cm,
BC=AB=9 cm.
又因为M为线段BC的中点,
所以CM=BC=4.5 cm,
所以AM=AC+CM=3+4.5=7.5(cm).
9.C 解析:因为∠1=15°,∠AOC=90°,所以∠BOC=∠AOC-∠1=90°-15°=75°.
因为∠2+∠BOC=∠BOD=180°,
所以∠2=180°-75°=105°.
10.B 解析:因为∠AOD=20°,∠COD=∠AOB=90°,所以∠COA=90°-20°=70°,所以∠BOC=∠COA+∠AOB=70°+90°=160°.
11.143°25′ 解析:180°-36°35′=179°60′-36°35′=143°25′.
12.1 解析:根据线段中点的定义可得,BC=AB=1.
13.29°25′12″ 解析:29.42°=29°+0.42°
=29°+(0.42×60)′
=29°+25.2′
=29°+25′+0.2′
=29°+25′+(0.2×60)″
=29°+25′+12″
=29°25′12″.
14.20° 解析:经过40 min,钟表的时针转过个大格,所以钟表的时针转过的角度为×=20°.
15.(1)北偏东70° 解析:因为OA是∠BOC的平分线,所以∠AOC=∠AOB=40°+15°=55°. 因为15°+55°=70°,所以OC的方向是北偏东70°.
(2)南偏东40°
16.(1)42° (2)不会 解析:∠MON=∠MOC+∠NOC-∠BOC+∠AOC-(∠BOC+∠AOC)-∠AOB=×84°=42°.
17.解:其中蕴含的数学道理是两点之间,线段最短.
18.解:如答图4-1所示.
19.解:从正面看可知货箱共有2层,结合从上面看得到的图形可知,第一层有4个货箱,结合从左面看得到的图形可知,第2层有1个货箱,所以这堆货箱共有5个.
20.解:因为D为线段AE的中点,且DE=6 cm,所以AE=2DE=12 cm.
(1)当点E在点A的右边时,如答图4-2,
CE=AE-AC=AE-AB=12-×15=4.5(cm).
(2)当点E在点A的左边时,如答图4-3,
CE=AE+AC=AE+AB=12+×15=19.5(cm).
综上所述,CE的长度为4.5 cm或19.5 cm.
21.解:方法l:因为∠DOE:∠BOE=1:3,
∠DOC:∠COA=1:3,
所以么∠BOE=3∠DOE,∠COA=3∠DOC,
所以∠BOD-4∠DOE,∠AOD=4∠DOC,
所以∠AOB=∠BOD+∠AOD
=4∠DOE+4∠DOC
=4(∠DOE+∠DOC)
=4∠COE=120°.
方法2:设∠DOE=x,∠COD=y,
则∠BOE=3x,∠COA=3y.
因为∠AOB=∠DOE+∠COD+∠BOE+∠COA,
所以∠AOB=4x+4y=4(x+y).
因为∠COE=∠DOE+∠COD=x+y,
所以∠AOB=4(x+y)=4∠COE=120°.
22.解:(1)灯塔S的位置如答网4-4所示.
(2)因为轮船从A处以20 km/h的速度向东行驶3 h到达B处,
所以AB的实际长度为20×3=60(km).
因此,图上1 cm表示实际长度20 km.
又量得SB≈2.6 cm,因此SB的实际长度约为52 km.
23.解:(1)从上到下填写表格依次为1,2,4,7.
(2)有规律,相邻两数的差依次为1,2,3,4,….
(3)当有n条直线时,最多把平面分成(1+1+2+3+…+n)部分,即部分.
(4)4刀.
