沪科版七年级上册 1.6有理数的乘方课件(共10张PPT)
文档属性
| 名称 | 沪科版七年级上册 1.6有理数的乘方课件(共10张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 309.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-25 00:00:00 | ||
图片预览



文档简介
(共13张PPT)
1.6 有理数的乘方
2
2
2
2
2
面积
体积
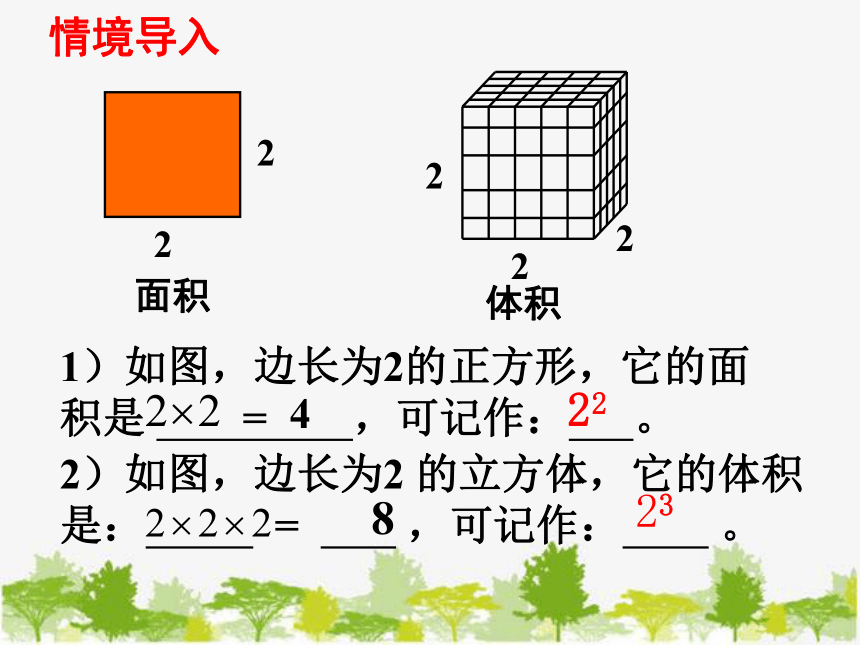
1)如图,边长为2的正方形,它的面积是 = ,可记作: 。
22
23
8
2)如图,边长为2 的立方体,它的体积是: = ,可记作: 。
4
情境导入
2 ×2 ×2 ×2 可记作: ,
2 ×2 ×2 ×2 ×2 可记 作: ,
2×2×······×2
n个2
可记 作: ,
a·a·a·…·a可记作: , 即a·a·a·……·a= .
n个a
n个a
24
25
2n
an
an
想一想:
1)上面各式具有什么共同特征?
2)说一说小学里学习的什么样的运算叫乘法?
你能仿照乘法的定义,说说什么样的运算叫乘方吗?试一试。
新知构建
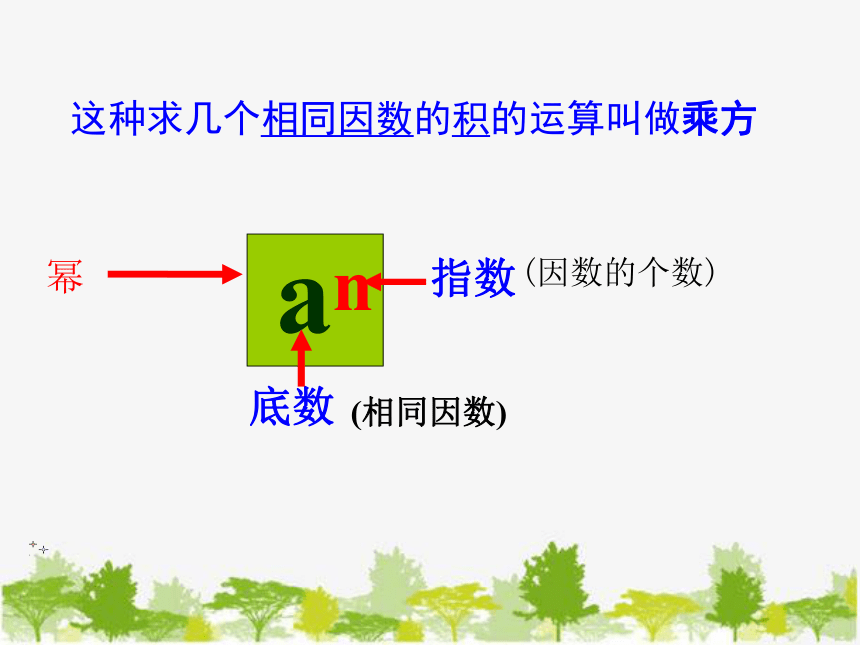
an
幂
指数
(因数的个数)
底数
(相同因数)
这种求几个相同因数的积的运算叫做乘方
1)把(-2.1)×(-2.1) ×(-2.1) ×(-2.1)
写成幂的形式是 ,
把 写成乘法运算的形式是: ;
2) 读作: , 或 ;
3的2次方
3的2次幂
3的平方
(-2.1)4
43
4×4×4
32
例题讲解
3)(-3)10的底数是____,指数是____;
-3
10
4) 的底数是 5 ,指数是 1 。
5) ( )7表示___个 相乘,叫做 的____次方,也叫做 的___次幂,其中
叫做____ ,7叫做____;
2
9
2
9
2
9
7
7
7
底数
指数
2
9
2
9
6) 与 意义相同吗?
(-2)3
-23
观察“做一做”的结果,你发现有理数乘方运算有什么规律,你能归纳出有理数乘方的法则吗?
1) = , = = , = = .
4
3×3
9
2×2×2
8
41
32
23
2) = ,
(-5)1
-5
= = ,
(-4)×(-4)
16
(-4)2
= = ,
(-3) ×(-3)×(-3)
-27
(-3)3
= = ,
(-2)4
(-2)×(-2)×(-2)×(-2)
16
= = ,
(-1)5
(-1)×(-1)×(-1)×(-1)×(-1)
-1
3) = , = , = ,
01
0
02
0
0
03
随堂练习
乘方运算法则:非零有理数的乘方,将其绝对值乘方,而结果的符号是:正数的任何次乘方都取正号;负数的奇次乘方取负号,负数的偶次乘方取正号。0的任何次方是0。
计算: 1)(-1)10, 2)(-1)7,
3)83, 4)(-5)3,
5)(-0.1)2, 6)(-
)4
小试牛刀
1)乘方的意义、分清底数、指数、幂;
2)乘方的运算法则。
课堂小结
1.6 有理数的乘方
2
2
2
2
2
面积
体积
1)如图,边长为2的正方形,它的面积是 = ,可记作: 。
22
23
8
2)如图,边长为2 的立方体,它的体积是: = ,可记作: 。
4
情境导入
2 ×2 ×2 ×2 可记作: ,
2 ×2 ×2 ×2 ×2 可记 作: ,
2×2×······×2
n个2
可记 作: ,
a·a·a·…·a可记作: , 即a·a·a·……·a= .
n个a
n个a
24
25
2n
an
an
想一想:
1)上面各式具有什么共同特征?
2)说一说小学里学习的什么样的运算叫乘法?
你能仿照乘法的定义,说说什么样的运算叫乘方吗?试一试。
新知构建
an
幂
指数
(因数的个数)
底数
(相同因数)
这种求几个相同因数的积的运算叫做乘方
1)把(-2.1)×(-2.1) ×(-2.1) ×(-2.1)
写成幂的形式是 ,
把 写成乘法运算的形式是: ;
2) 读作: , 或 ;
3的2次方
3的2次幂
3的平方
(-2.1)4
43
4×4×4
32
例题讲解
3)(-3)10的底数是____,指数是____;
-3
10
4) 的底数是 5 ,指数是 1 。
5) ( )7表示___个 相乘,叫做 的____次方,也叫做 的___次幂,其中
叫做____ ,7叫做____;
2
9
2
9
2
9
7
7
7
底数
指数
2
9
2
9
6) 与 意义相同吗?
(-2)3
-23
观察“做一做”的结果,你发现有理数乘方运算有什么规律,你能归纳出有理数乘方的法则吗?
1) = , = = , = = .
4
3×3
9
2×2×2
8
41
32
23
2) = ,
(-5)1
-5
= = ,
(-4)×(-4)
16
(-4)2
= = ,
(-3) ×(-3)×(-3)
-27
(-3)3
= = ,
(-2)4
(-2)×(-2)×(-2)×(-2)
16
= = ,
(-1)5
(-1)×(-1)×(-1)×(-1)×(-1)
-1
3) = , = , = ,
01
0
02
0
0
03
随堂练习
乘方运算法则:非零有理数的乘方,将其绝对值乘方,而结果的符号是:正数的任何次乘方都取正号;负数的奇次乘方取负号,负数的偶次乘方取正号。0的任何次方是0。
计算: 1)(-1)10, 2)(-1)7,
3)83, 4)(-5)3,
5)(-0.1)2, 6)(-
)4
小试牛刀
1)乘方的意义、分清底数、指数、幂;
2)乘方的运算法则。
课堂小结
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
