2022—2023学年人教版数学九年级上册24.2.2直线和圆的位置关系同步练习(含答案)
文档属性
| 名称 | 2022—2023学年人教版数学九年级上册24.2.2直线和圆的位置关系同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 372.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-25 00:00:00 | ||
图片预览




文档简介
24.2.2 直线和圆的位置关系
班级: 姓名: 成绩:
一、选择题
1.已知⊙O的半径是7cm,点O到同一平面内直线l的距离为6.9cm,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法判断
2.直角△ABC,∠BAC=90°,AB=8,AC=6,以A为圆心,4.8长度为半径的圆与直线BC的公共点的个数为( )
A.0 B.1 C.2 D.不能确定
3.如图,OA是⊙О的一条半径,点P是OA延长线上一点,过点P作⊙O的切线PB,点B为切点. 若PA=1,PB=2,则半径OA的长为( )
A. B. C. D.3
4.已知⊙O的半径为4,点O到直线l的距离为d若直线l与⊙O的公共点的个数为2个则d的值不能为( )
A.0 B.2 C.3 D.5
5.如图,已知中,,,,如果以点为圆心的圆与斜边有公共点,那么⊙的半径的取值范围是( )
A. B. C. D.
6.已知⊙O与直线l无公共点,若⊙O直径为10cm,则圆心O到直线l的距离可以是( )
A.6 B.5 C.4 D.3
7.如图,在平面直角坐标系中,半径为2的⊙P的圆心P的坐标为(﹣3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为( )
A.1或5 B.1或3 C.3或5 D.1
8.如图,直线AB、CD相交于点O,∠AOC=30°,半径为2cm的P的圆心在射线OA上,且与点O的距离为6cm,如果P以1cm/s的速度沿直线AB由A向B的方向移动,那么P与直线CD相切时☉P运动的时间是( )
A.3秒或10秒 B.3秒或8秒 C.2秒或8秒 D.2秒或10秒
9.如图,在半径为5cm的⊙O中,直线l交⊙O于A、B两点,且弦AB=8cm,要使直线l与⊙O相切,则需要将直线l向下平移( )
A.1cm B.2cm C.3cm D.4cm
10.如图,在平面直角坐标系中,P是直线y=2上的一个动点,⊙P的半径为1,直线OQ切⊙P于点Q,则线段OQ的最小值为( )
A.1 B.2 C. D.
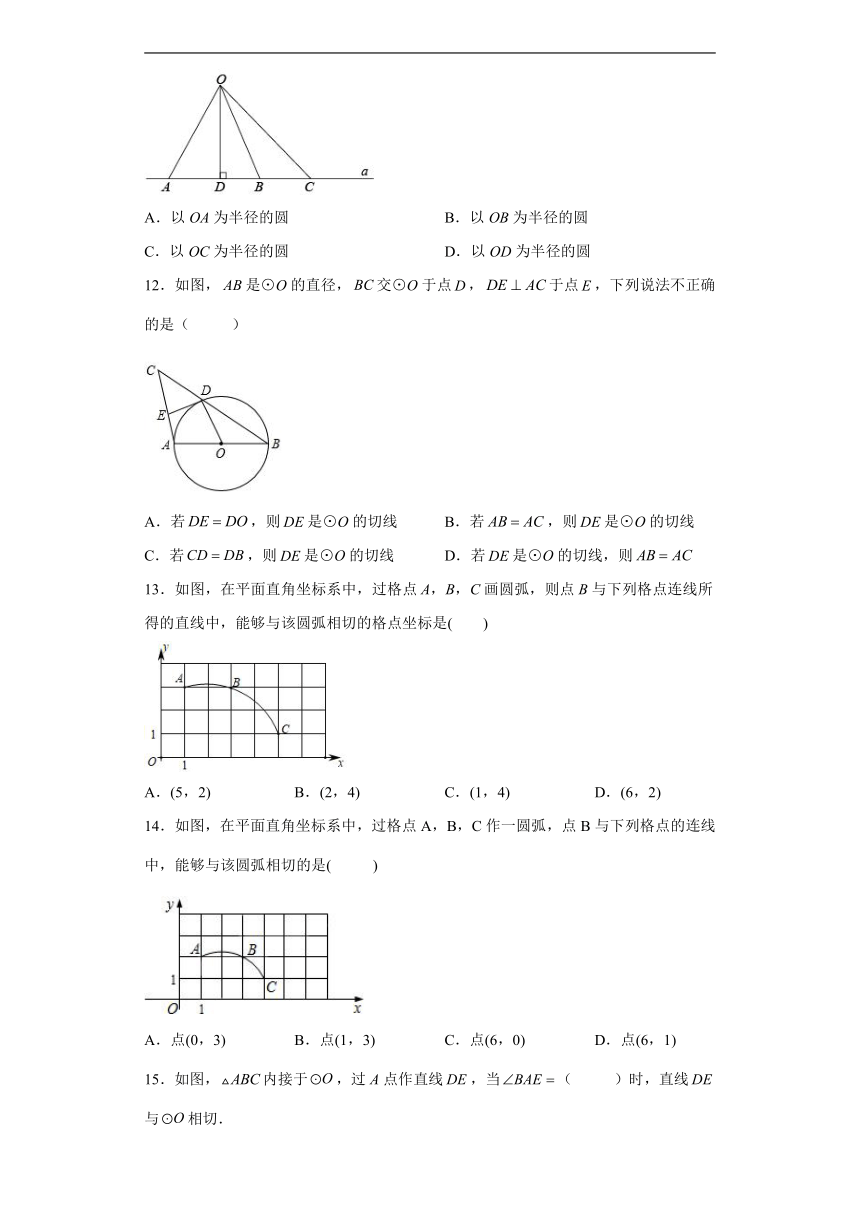
11.如图,以点O为圆心作圆,所得的圆与直线a相切的是( )
A.以OA为半径的圆 B.以OB为半径的圆
C.以OC为半径的圆 D.以OD为半径的圆
12.如图,是⊙O的直径,交⊙O于点,于点,下列说法不正确的是( )
A.若,则是⊙O的切线 B.若,则是⊙O的切线
C.若,则是⊙O的切线 D.若是⊙O的切线,则
13.如图,在平面直角坐标系中,过格点A,B,C画圆弧,则点B与下列格点连线所得的直线中,能够与该圆弧相切的格点坐标是( )
A.(5,2) B.(2,4) C.(1,4) D.(6,2)
14.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )
A.点(0,3) B.点(1,3) C.点(6,0) D.点(6,1)
15.如图,内接于,过A点作直线,当( )时,直线与相切.
A. B. C. D.
16.如图,AB是⊙O的直径,C、D是⊙O上一点,∠CDB=25°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( )
A.40° B.50° C.60° D.70°
17.如图,是的内接三角形,过点C的的切线交BO的延长线于点P,若,那么度数为( )
A. B. C. D.
18.如图,PA,PB切⊙O 于点A,B,PA=20,CD切⊙O于点E,交PA,PB于C,D两点,则△PCD 的周长是( )
A.20 B.36 C.40 D.44
19.如图PA、PB是圆O的切线,切点分别为A、B,点C在AB上,过C作圆O的切线分别交PA、PB于点D、E,连接OD、OE,若∠P=50°,则∠DOE的度数为( )
A.130° B.50° C.60° D.65°
20.如图,在中,,于D,⊙O为的内切圆,设⊙O的半径为R,AD的长为h,则的值为( )
A. B. C. D.
21.我国古代数学名著《九章算术》中有“勾股定理”问题:“今有勾八步,股十五步,问勾中容圆径几何?”其意思是“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少步?”此问题的答案是 ( ).
A.3步 B.4步 C.6步 D.8步
二、填空题
22.设⊙O的半径为4cm,直线L上一点A到圆心的距离为4cm,则直线L与⊙O的位置关系是______.
23.如图,点D是等腰直角△ABC斜边AB上一点,点E是BC上一点,AB=2,DA=DE,则AD的取值范围是____.
24.如图,半径为5个单位的⊙A与x轴、y轴都相切;现将⊙A沿y轴向下平移 ___个单位后圆与x轴交于点(2,0).
25.如图,圆心O恰好为正方形ABCD的中心,已知AB=10,⊙O的半径为1,现将⊙O在正方形内部沿某一方向平移,当它与正方形ABCD的某条边相切时停止平移,设此时的平移的距离为d,则d的取值范围是_______.
26.一动点在二次函数的图像上自由滑动,若以点为圆心,1为半径的圆与坐标轴相切,则点的坐标为______.
27.在下图中,是的直径,要使得直线是的切线,需要添加的一个条件是________.(写一个条件即可)
28.如图,PA,PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠AOB=120°,则AB=_____.
三、解答题
29.如图所示,在平面直角坐标系xOy中,半径为2的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,求平移的距离.
30.如图,△ABC的边AB为⊙O的直径,BC与⊙O交于点D,D为BC的中点,连接AD,过D作DE⊥AC于E.
(1)求证:DE为⊙O的切线;
(2)若AB=13,CD=5,求DE的长.
31.如图,直线AB与⊙O相切于点B,直线AO交⊙O于D,E两点,BC⊥DE于点C,DF⊥AB于点F.求证:DC=DF.
32.如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,过点D作AD的垂线交AB于点E.
(1)请画出△ADE的外接圆⊙O(尺规作图,不写作法,保留作图痕迹);
(2)求证:BC是⊙O的切线;
(3)过点D作DF⊥AE于点F,延长DF交⊙O于点G,若DG=8,EF=2.求⊙O的半径.
试卷第1页,共3页
参考答案
1.A
2.B
3.B
4.D
5.C
6.A
7.A
8.D
9.B
10.C
11.D
12.A
13.D
14.B
15.C
16.A
17.B
18.C
19.D
20.B
21.C
22.相切或相交
23.
24.1或9
25.4≤d≤
26.或或
27.∠ABT=∠ATB=45°(答案不唯一)
28.6
29.1或5.
30.(1)证明:连接OD,
∵BO=OA,BD=DC,
∴OD//AC,
∵DE⊥AC,
∴OD⊥DE,
∴DE为⊙O的切线;
(2)∴AD⊥BD,
∵BD=CD=5,
∴AC=AB=13,
∴AD===12,
∵
∴,
解得:DE=,
31.证明:如图,连接OB,
∵AB与⊙O相切于点B,
∴OB⊥AB,
∴∠OBA=∠OBD+∠ABD=90°,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠ODB+∠ABD=90°,
∵BC⊥DE,
∴∠CBD+∠ODB=90°,
∴∠CBD=∠ABD,
∴BD平分∠ABC,
∵BC⊥DE,DF⊥AB,
∴DC=DF.
32.
解:如图1所示,⊙O即为所求;
证明:如图2,
连接OD,∵AD平分∠CAB,∴∠CAD=∠OAD,∵OA=OD,∴∠OAD=∠ODA,∴∠CAD=∠ODA,∴OD∥AC,∵∠C=90°,∴OD⊥BC,∵OD为⊙O的半径,∴BC是⊙O的切线;
解:设⊙O的半径为r,∵DF⊥AE,∴DF=GFDG=4,在Rt△ODF中,∠OFD=90°,OD=r,OF=r﹣2,DF=4,∴r2=(r﹣2)2+42,r=5,∴⊙O的半径为5.
班级: 姓名: 成绩:
一、选择题
1.已知⊙O的半径是7cm,点O到同一平面内直线l的距离为6.9cm,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法判断
2.直角△ABC,∠BAC=90°,AB=8,AC=6,以A为圆心,4.8长度为半径的圆与直线BC的公共点的个数为( )
A.0 B.1 C.2 D.不能确定
3.如图,OA是⊙О的一条半径,点P是OA延长线上一点,过点P作⊙O的切线PB,点B为切点. 若PA=1,PB=2,则半径OA的长为( )
A. B. C. D.3
4.已知⊙O的半径为4,点O到直线l的距离为d若直线l与⊙O的公共点的个数为2个则d的值不能为( )
A.0 B.2 C.3 D.5
5.如图,已知中,,,,如果以点为圆心的圆与斜边有公共点,那么⊙的半径的取值范围是( )
A. B. C. D.
6.已知⊙O与直线l无公共点,若⊙O直径为10cm,则圆心O到直线l的距离可以是( )
A.6 B.5 C.4 D.3
7.如图,在平面直角坐标系中,半径为2的⊙P的圆心P的坐标为(﹣3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为( )
A.1或5 B.1或3 C.3或5 D.1
8.如图,直线AB、CD相交于点O,∠AOC=30°,半径为2cm的P的圆心在射线OA上,且与点O的距离为6cm,如果P以1cm/s的速度沿直线AB由A向B的方向移动,那么P与直线CD相切时☉P运动的时间是( )
A.3秒或10秒 B.3秒或8秒 C.2秒或8秒 D.2秒或10秒
9.如图,在半径为5cm的⊙O中,直线l交⊙O于A、B两点,且弦AB=8cm,要使直线l与⊙O相切,则需要将直线l向下平移( )
A.1cm B.2cm C.3cm D.4cm
10.如图,在平面直角坐标系中,P是直线y=2上的一个动点,⊙P的半径为1,直线OQ切⊙P于点Q,则线段OQ的最小值为( )
A.1 B.2 C. D.
11.如图,以点O为圆心作圆,所得的圆与直线a相切的是( )
A.以OA为半径的圆 B.以OB为半径的圆
C.以OC为半径的圆 D.以OD为半径的圆
12.如图,是⊙O的直径,交⊙O于点,于点,下列说法不正确的是( )
A.若,则是⊙O的切线 B.若,则是⊙O的切线
C.若,则是⊙O的切线 D.若是⊙O的切线,则
13.如图,在平面直角坐标系中,过格点A,B,C画圆弧,则点B与下列格点连线所得的直线中,能够与该圆弧相切的格点坐标是( )
A.(5,2) B.(2,4) C.(1,4) D.(6,2)
14.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )
A.点(0,3) B.点(1,3) C.点(6,0) D.点(6,1)
15.如图,内接于,过A点作直线,当( )时,直线与相切.
A. B. C. D.
16.如图,AB是⊙O的直径,C、D是⊙O上一点,∠CDB=25°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( )
A.40° B.50° C.60° D.70°
17.如图,是的内接三角形,过点C的的切线交BO的延长线于点P,若,那么度数为( )
A. B. C. D.
18.如图,PA,PB切⊙O 于点A,B,PA=20,CD切⊙O于点E,交PA,PB于C,D两点,则△PCD 的周长是( )
A.20 B.36 C.40 D.44
19.如图PA、PB是圆O的切线,切点分别为A、B,点C在AB上,过C作圆O的切线分别交PA、PB于点D、E,连接OD、OE,若∠P=50°,则∠DOE的度数为( )
A.130° B.50° C.60° D.65°
20.如图,在中,,于D,⊙O为的内切圆,设⊙O的半径为R,AD的长为h,则的值为( )
A. B. C. D.
21.我国古代数学名著《九章算术》中有“勾股定理”问题:“今有勾八步,股十五步,问勾中容圆径几何?”其意思是“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少步?”此问题的答案是 ( ).
A.3步 B.4步 C.6步 D.8步
二、填空题
22.设⊙O的半径为4cm,直线L上一点A到圆心的距离为4cm,则直线L与⊙O的位置关系是______.
23.如图,点D是等腰直角△ABC斜边AB上一点,点E是BC上一点,AB=2,DA=DE,则AD的取值范围是____.
24.如图,半径为5个单位的⊙A与x轴、y轴都相切;现将⊙A沿y轴向下平移 ___个单位后圆与x轴交于点(2,0).
25.如图,圆心O恰好为正方形ABCD的中心,已知AB=10,⊙O的半径为1,现将⊙O在正方形内部沿某一方向平移,当它与正方形ABCD的某条边相切时停止平移,设此时的平移的距离为d,则d的取值范围是_______.
26.一动点在二次函数的图像上自由滑动,若以点为圆心,1为半径的圆与坐标轴相切,则点的坐标为______.
27.在下图中,是的直径,要使得直线是的切线,需要添加的一个条件是________.(写一个条件即可)
28.如图,PA,PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠AOB=120°,则AB=_____.
三、解答题
29.如图所示,在平面直角坐标系xOy中,半径为2的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,求平移的距离.
30.如图,△ABC的边AB为⊙O的直径,BC与⊙O交于点D,D为BC的中点,连接AD,过D作DE⊥AC于E.
(1)求证:DE为⊙O的切线;
(2)若AB=13,CD=5,求DE的长.
31.如图,直线AB与⊙O相切于点B,直线AO交⊙O于D,E两点,BC⊥DE于点C,DF⊥AB于点F.求证:DC=DF.
32.如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,过点D作AD的垂线交AB于点E.
(1)请画出△ADE的外接圆⊙O(尺规作图,不写作法,保留作图痕迹);
(2)求证:BC是⊙O的切线;
(3)过点D作DF⊥AE于点F,延长DF交⊙O于点G,若DG=8,EF=2.求⊙O的半径.
试卷第1页,共3页
参考答案
1.A
2.B
3.B
4.D
5.C
6.A
7.A
8.D
9.B
10.C
11.D
12.A
13.D
14.B
15.C
16.A
17.B
18.C
19.D
20.B
21.C
22.相切或相交
23.
24.1或9
25.4≤d≤
26.或或
27.∠ABT=∠ATB=45°(答案不唯一)
28.6
29.1或5.
30.(1)证明:连接OD,
∵BO=OA,BD=DC,
∴OD//AC,
∵DE⊥AC,
∴OD⊥DE,
∴DE为⊙O的切线;
(2)∴AD⊥BD,
∵BD=CD=5,
∴AC=AB=13,
∴AD===12,
∵
∴,
解得:DE=,
31.证明:如图,连接OB,
∵AB与⊙O相切于点B,
∴OB⊥AB,
∴∠OBA=∠OBD+∠ABD=90°,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠ODB+∠ABD=90°,
∵BC⊥DE,
∴∠CBD+∠ODB=90°,
∴∠CBD=∠ABD,
∴BD平分∠ABC,
∵BC⊥DE,DF⊥AB,
∴DC=DF.
32.
解:如图1所示,⊙O即为所求;
证明:如图2,
连接OD,∵AD平分∠CAB,∴∠CAD=∠OAD,∵OA=OD,∴∠OAD=∠ODA,∴∠CAD=∠ODA,∴OD∥AC,∵∠C=90°,∴OD⊥BC,∵OD为⊙O的半径,∴BC是⊙O的切线;
解:设⊙O的半径为r,∵DF⊥AE,∴DF=GFDG=4,在Rt△ODF中,∠OFD=90°,OD=r,OF=r﹣2,DF=4,∴r2=(r﹣2)2+42,r=5,∴⊙O的半径为5.
同课章节目录
