2022-2023学年京改版八年级数学上册12.10 轴对称和轴对称图形 课堂提升训练(含答案)
文档属性
| 名称 | 2022-2023学年京改版八年级数学上册12.10 轴对称和轴对称图形 课堂提升训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 644.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-25 17:00:28 | ||
图片预览


文档简介
2022-2023学年度北京课改版版八年级数学上册
课堂提升训练
第十二章 三角形
四 尺规作图及轴对称
12.10 轴对称和轴对称图形
基础过关全练
知识点1 轴对称及轴对称图形的概念
1.(2022独家原创)京剧是我国的国粹,下列用于舞台表演的脸谱中属于轴对称图形的个数是( )
A.1 B.2 C.3 D.4
2.下列图形中,△A'B'C'与△ABC关于直线MN成轴对称的是( )
A B C D
3.(2021安徽亳州期末)下面四个手机应用的图标是轴对称图形的为( )
A B C D
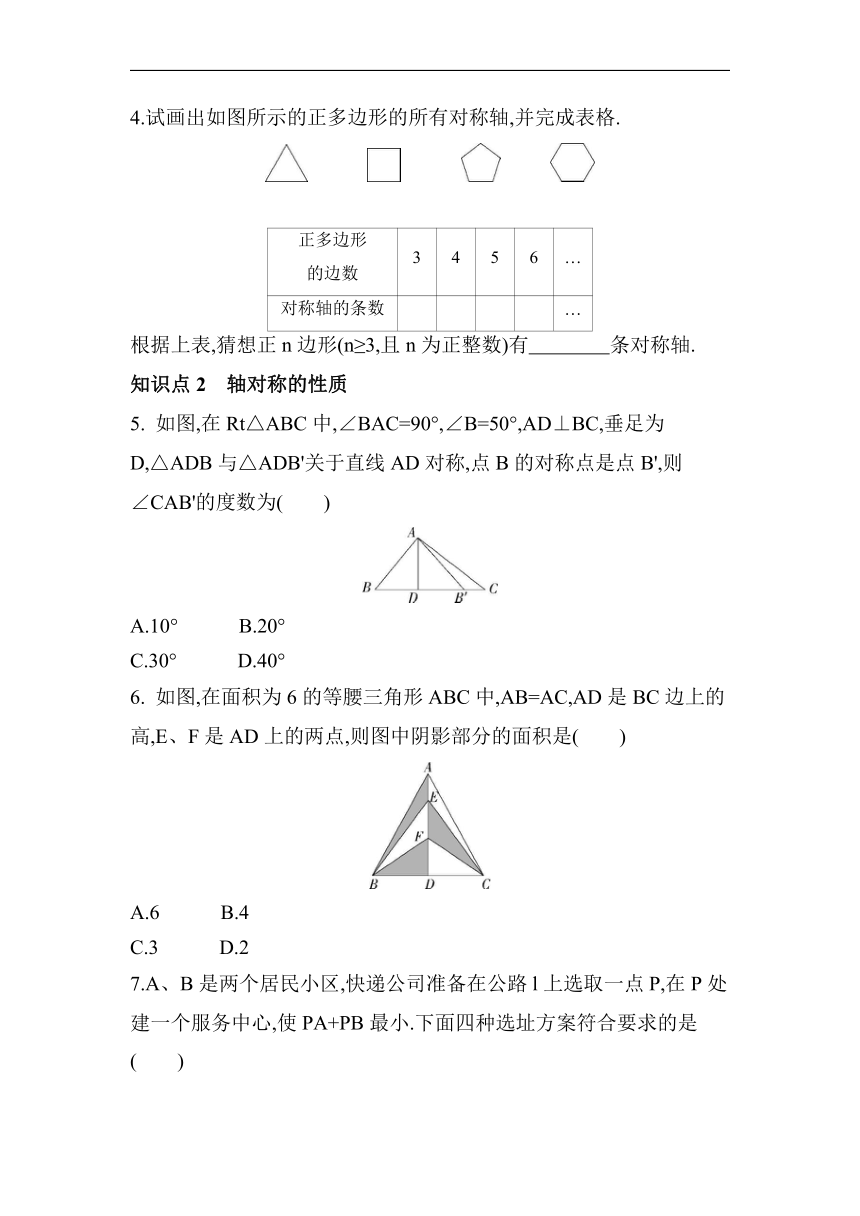
4.试画出如图所示的正多边形的所有对称轴,并完成表格.
正多边形 的边数 3 4 5 6 …
对称轴的条数 …
根据上表,猜想正n边形(n≥3,且n为正整数)有 条对称轴.
知识点2 轴对称的性质
5. 如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为( )
A.10° B.20°
C.30° D.40°
6. 如图,在面积为6的等腰三角形ABC中,AB=AC,AD是BC边上的高,E、F是AD上的两点,则图中阴影部分的面积是( )
A.6 B.4
C.3 D.2
7.A、B是两个居民小区,快递公司准备在公路l上选取一点P,在P处建一个服务中心,使PA+PB最小.下面四种选址方案符合要求的是( )
A B C D
8.(2022北京西城期中)如图,△ABC中,点D在BC上,将点D分别以AB、AC所在直线为对称轴对称,得到点E、F,连接AE、AF.若∠B=62°,∠C=51°,则∠EAF的度数为 .
9. 如图,∠MON=60°,点A是OM边上一点,点B,C是ON边上两点,且AB=AC,作点B关于OM的对称点D,连接AD,CD,OD.
(1)依题意补全图形;
(2)猜想∠DAC= °,并证明;
(3)猜想线段OA、OD、OC的数量关系,并证明.
能力提升全练
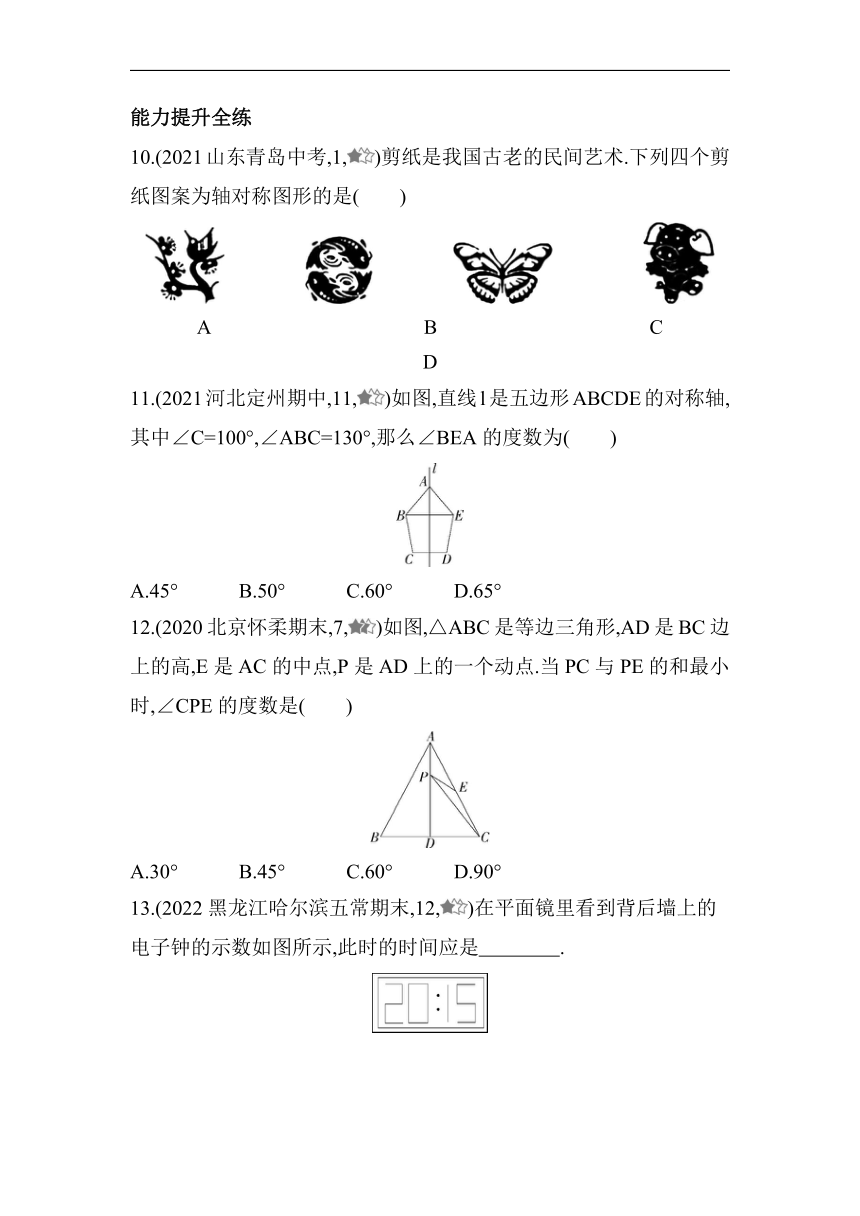
10.(2021山东青岛中考,1,)剪纸是我国古老的民间艺术.下列四个剪纸图案为轴对称图形的是( )
A B C D
11.(2021河北定州期中,11,)如图,直线l是五边形ABCDE的对称轴,其中∠C=100°,∠ABC=130°,那么∠BEA的度数为( )
A.45° B.50° C.60° D.65°
12.(2020北京怀柔期末,7,)如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点.当PC与PE的和最小时,∠CPE的度数是( )
A.30° B.45° C.60° D.90°
13.(2022黑龙江哈尔滨五常期末,12,)在平面镜里看到背后墙上的电子钟的示数如图所示,此时的时间应是 .
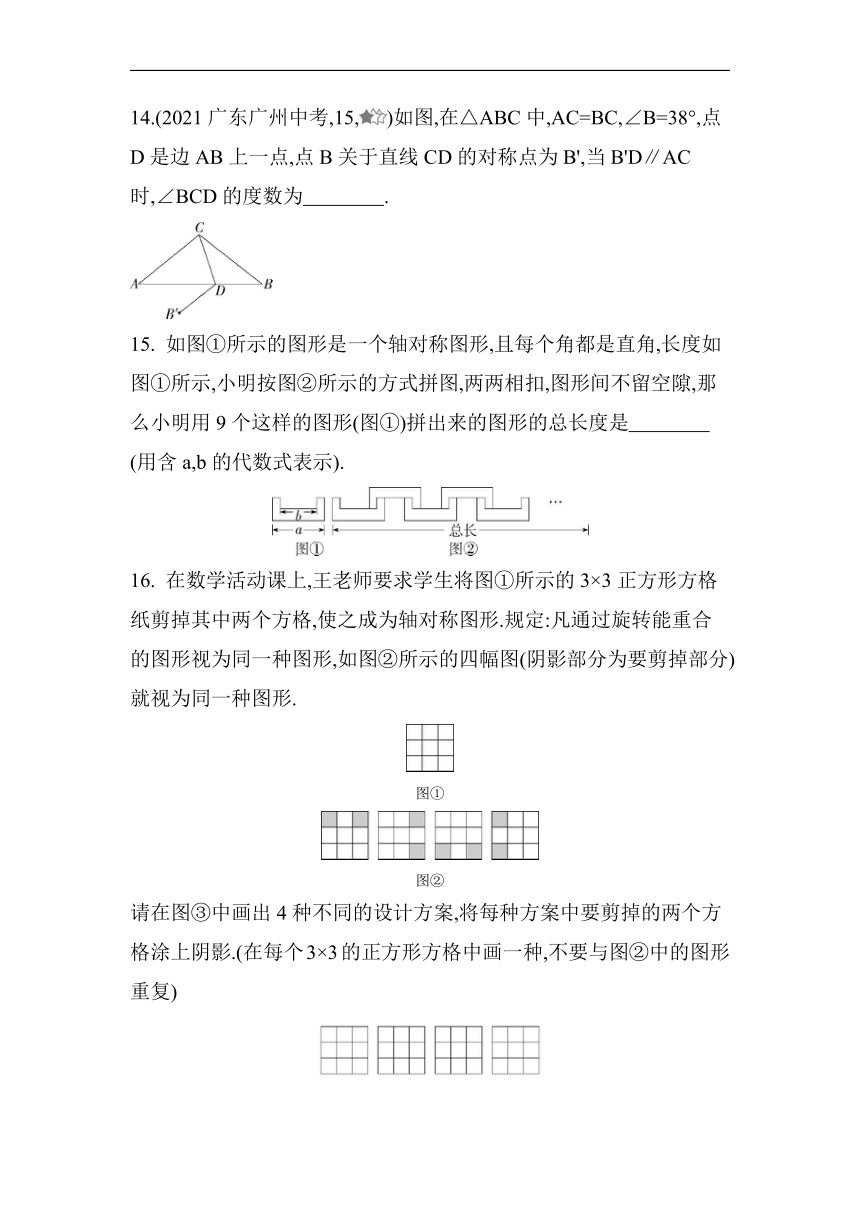
14.(2021广东广州中考,15,)如图,在△ABC中,AC=BC,∠B=38°,点D是边AB上一点,点B关于直线CD的对称点为B',当B'D∥AC时,∠BCD的度数为 .
15. 如图①所示的图形是一个轴对称图形,且每个角都是直角,长度如图①所示,小明按图②所示的方式拼图,两两相扣,图形间不留空隙,那么小明用9个这样的图形(图①)拼出来的图形的总长度是 (用含a,b的代数式表示).
16. 在数学活动课上,王老师要求学生将图①所示的3×3正方形方格纸剪掉其中两个方格,使之成为轴对称图形.规定:凡通过旋转能重合的图形视为同一种图形,如图②所示的四幅图(阴影部分为要剪掉部分)就视为同一种图形.
图①
图②
请在图③中画出4种不同的设计方案,将每种方案中要剪掉的两个方格涂上阴影.(在每个3×3的正方形方格中画一种,不要与图②中的图形重复)
图③
素养探究全练
17. 已知点P为∠O内一定点,分别在∠O的两边上找点A、B,使△PAB的周长最小的是( )
A B C D
18. (2021北京朝阳期中)如图,△ABC中,∠ABC=45°,点A关于直线BC的对称点为P,连接PB.过点C作CD⊥AC,交射线PB于点D.
(1)如图①,当∠ACB为钝角时,补全图形,判断AC与CD的数量关系,并说明理由;
(2)如图②,当∠ACB为锐角时,补全图形,判断(1)中的结论是否仍成立,并说明理由.
图① 图②
答案全解全析
基础过关全练
1.B 根据轴对称图形的概念可知,从左至右第1个和第3个脸谱是轴对称图形,共2个.
2.B 根据轴对称的概念可知,沿直线MN翻折,△A'B'C'与△ABC能够完全重合的只有选项B.
3.D 依据轴对称图形的概念可知,选项A、B、C都不符合题意,只有选项D符合题意.
4.解析 如图所示:
题表中从左到右依次填:3;4;5;6.
正n边形有n条对称轴.
5.A ∵∠BAC=90°,∠B=50°,∴∠C=40°,由轴对称的性质可得∠AB'B=∠B=50°,∴∠CAB'=∠AB'B-∠C=10°,故选A.
6.C 根据等腰三角形是轴对称图形,且AD⊥BC可知,△CEF和△BEF的面积相等,所以阴影部分的面积是△ABC的面积的一半.所以阴影部分的面积为3.故选C.
7.A 根据题意,要求在公路l上选取点P,使PA+PB最小,选项A中的选址方案符合要求.
8.134°
解析 如图,连接AD,
由轴对称的性质可知,∠EAB=∠BAD,∠FAC=∠CAD,
∵∠B=62°,∠C=51°,
∴∠BAD+∠DAC=∠BAC=180°-62°-51°=67°,
∴∠EAF=∠EAB+∠FAC+∠BAD+∠DAC=2(∠BAD+∠DAC)=134°.
9.解析 (1)补全图形如图所示:
(2)∠DAC=60°.证明:如图,作AH⊥BC于H,
∵AB=AC,AH⊥BC,∴∠BAC=2∠1.
∵点B与点D关于OM对称,∴∠DAB=2∠2.
∵∠AOB=60°,∠AHO=90°,
∴∠OAH=30°,即∠1+∠2=30°,
∴∠DAC=∠BAC+∠DAB=2(∠1+∠2)=60°.
(3)OA=OD+OC.
证明:如图,在ON上取一点P,使得OP=OA,连接AP,
∵∠AOP=60°,点B与点D关于OM对称,
∴△AOP是等边三角形,∠AOD=60°,
∴∠OAP=∠APO=∠AOD=60°,AP=AO.
∵∠OAP=∠DAC=60°,∴∠DAO=∠CAP.
在△ADO和△ACP中,
∴△ADO≌△ACP(ASA),
∴OD=PC,∴OA=OP=PC+OC=OD+OC.
能力提升全练
10.C 根据轴对称图形的概念可知只有选项C中的剪纸图案是轴对称图形.故选C.
11.B ∵直线l是五边形ABCDE的对称轴,∴∠ABE=∠AEB,∠AED=∠ABC=130°,∠D=∠C=100°,
∴∠BAE=540°-130°×2-100°×2=80°,∴∠BEA=×(180°-80°)=50°.
12.C 如图,连接BE,BE与AD交于点P,此时PE+PC最小.
∵△ABC是等边三角形,∴∠BCE=60°,BA=BC.
∵E是AC的中点,∴BE⊥AC,∴∠BEC=90°,
∴∠EBC=30°.
∵△ABC是等边三角形,AD⊥BC,∴BD=CD,
∴AD垂直平分BC,∴BP=CP,∴∠PCB=∠PBC=30°,∴∠CPE=∠PBC+∠PCB=60°.
13.21:05
解析 “”与“”成轴对称,故此时的时间应是21:05.
14.33°
解析 ∵AC=BC,∴∠A=∠B=38°,
∵B'D∥AC,∴∠ADB'=∠A=38°,
∵点B关于直线CD的对称点为B',
∴∠CDB'=∠CDB=×(38°+180°)=109°,
∴∠BCD=180°-38°-109°=33°.
15.a+8b
解析 由题图可得,拼出来的图形的总长度=9a-8(a-b)=a+8b.
16.解析 如图所示.(答案不唯一)
素养探究全练
17.D 分别在∠O的两边上找点A、B,使△PAB的周长最小的是D选项.
18.解析 (1)补全图形后如图①所示,AC与CD的数量关系为AC=CD.
理由:如图①,连接CP,设AB交CD于O,
∵A,P关于直线BC对称,∴CP=CA,∠P=∠A,∠CBP=∠ABC=45°,
∴∠ABP=90°,∴∠ABD=90°,
∵AC⊥CD,∴∠ACO=90°,∴∠ACO=∠DBO,
∵∠AOC=∠DOB,∴∠D=∠A,
∵∠P=∠A,∴∠D=∠P,∴CD=CP,∴AC=CD.
(2)补全图形后如图②所示,AC与CD的数量关系仍为AC=CD.理由:如图②,连接CP,
∵A,P关于直线BC对称,
∴CP=CA,∠P=∠A,∠CBP=∠ABC=45°,
∴∠ABP=90°,
∵AC⊥CD,∴∠ACD=90°,
∴∠ABD+∠ACD=180°,∴∠A+∠BDC=180°,
∵∠CDP+∠BDC=180°,∴∠A=∠CDP,
∵∠P=∠A,∴∠CDP=∠P,∴CD=CP,∴AC=CD.
图① 图②
课堂提升训练
第十二章 三角形
四 尺规作图及轴对称
12.10 轴对称和轴对称图形
基础过关全练
知识点1 轴对称及轴对称图形的概念
1.(2022独家原创)京剧是我国的国粹,下列用于舞台表演的脸谱中属于轴对称图形的个数是( )
A.1 B.2 C.3 D.4
2.下列图形中,△A'B'C'与△ABC关于直线MN成轴对称的是( )
A B C D
3.(2021安徽亳州期末)下面四个手机应用的图标是轴对称图形的为( )
A B C D
4.试画出如图所示的正多边形的所有对称轴,并完成表格.
正多边形 的边数 3 4 5 6 …
对称轴的条数 …
根据上表,猜想正n边形(n≥3,且n为正整数)有 条对称轴.
知识点2 轴对称的性质
5. 如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为( )
A.10° B.20°
C.30° D.40°
6. 如图,在面积为6的等腰三角形ABC中,AB=AC,AD是BC边上的高,E、F是AD上的两点,则图中阴影部分的面积是( )
A.6 B.4
C.3 D.2
7.A、B是两个居民小区,快递公司准备在公路l上选取一点P,在P处建一个服务中心,使PA+PB最小.下面四种选址方案符合要求的是( )
A B C D
8.(2022北京西城期中)如图,△ABC中,点D在BC上,将点D分别以AB、AC所在直线为对称轴对称,得到点E、F,连接AE、AF.若∠B=62°,∠C=51°,则∠EAF的度数为 .
9. 如图,∠MON=60°,点A是OM边上一点,点B,C是ON边上两点,且AB=AC,作点B关于OM的对称点D,连接AD,CD,OD.
(1)依题意补全图形;
(2)猜想∠DAC= °,并证明;
(3)猜想线段OA、OD、OC的数量关系,并证明.
能力提升全练
10.(2021山东青岛中考,1,)剪纸是我国古老的民间艺术.下列四个剪纸图案为轴对称图形的是( )
A B C D
11.(2021河北定州期中,11,)如图,直线l是五边形ABCDE的对称轴,其中∠C=100°,∠ABC=130°,那么∠BEA的度数为( )
A.45° B.50° C.60° D.65°
12.(2020北京怀柔期末,7,)如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点.当PC与PE的和最小时,∠CPE的度数是( )
A.30° B.45° C.60° D.90°
13.(2022黑龙江哈尔滨五常期末,12,)在平面镜里看到背后墙上的电子钟的示数如图所示,此时的时间应是 .
14.(2021广东广州中考,15,)如图,在△ABC中,AC=BC,∠B=38°,点D是边AB上一点,点B关于直线CD的对称点为B',当B'D∥AC时,∠BCD的度数为 .
15. 如图①所示的图形是一个轴对称图形,且每个角都是直角,长度如图①所示,小明按图②所示的方式拼图,两两相扣,图形间不留空隙,那么小明用9个这样的图形(图①)拼出来的图形的总长度是 (用含a,b的代数式表示).
16. 在数学活动课上,王老师要求学生将图①所示的3×3正方形方格纸剪掉其中两个方格,使之成为轴对称图形.规定:凡通过旋转能重合的图形视为同一种图形,如图②所示的四幅图(阴影部分为要剪掉部分)就视为同一种图形.
图①
图②
请在图③中画出4种不同的设计方案,将每种方案中要剪掉的两个方格涂上阴影.(在每个3×3的正方形方格中画一种,不要与图②中的图形重复)
图③
素养探究全练
17. 已知点P为∠O内一定点,分别在∠O的两边上找点A、B,使△PAB的周长最小的是( )
A B C D
18. (2021北京朝阳期中)如图,△ABC中,∠ABC=45°,点A关于直线BC的对称点为P,连接PB.过点C作CD⊥AC,交射线PB于点D.
(1)如图①,当∠ACB为钝角时,补全图形,判断AC与CD的数量关系,并说明理由;
(2)如图②,当∠ACB为锐角时,补全图形,判断(1)中的结论是否仍成立,并说明理由.
图① 图②
答案全解全析
基础过关全练
1.B 根据轴对称图形的概念可知,从左至右第1个和第3个脸谱是轴对称图形,共2个.
2.B 根据轴对称的概念可知,沿直线MN翻折,△A'B'C'与△ABC能够完全重合的只有选项B.
3.D 依据轴对称图形的概念可知,选项A、B、C都不符合题意,只有选项D符合题意.
4.解析 如图所示:
题表中从左到右依次填:3;4;5;6.
正n边形有n条对称轴.
5.A ∵∠BAC=90°,∠B=50°,∴∠C=40°,由轴对称的性质可得∠AB'B=∠B=50°,∴∠CAB'=∠AB'B-∠C=10°,故选A.
6.C 根据等腰三角形是轴对称图形,且AD⊥BC可知,△CEF和△BEF的面积相等,所以阴影部分的面积是△ABC的面积的一半.所以阴影部分的面积为3.故选C.
7.A 根据题意,要求在公路l上选取点P,使PA+PB最小,选项A中的选址方案符合要求.
8.134°
解析 如图,连接AD,
由轴对称的性质可知,∠EAB=∠BAD,∠FAC=∠CAD,
∵∠B=62°,∠C=51°,
∴∠BAD+∠DAC=∠BAC=180°-62°-51°=67°,
∴∠EAF=∠EAB+∠FAC+∠BAD+∠DAC=2(∠BAD+∠DAC)=134°.
9.解析 (1)补全图形如图所示:
(2)∠DAC=60°.证明:如图,作AH⊥BC于H,
∵AB=AC,AH⊥BC,∴∠BAC=2∠1.
∵点B与点D关于OM对称,∴∠DAB=2∠2.
∵∠AOB=60°,∠AHO=90°,
∴∠OAH=30°,即∠1+∠2=30°,
∴∠DAC=∠BAC+∠DAB=2(∠1+∠2)=60°.
(3)OA=OD+OC.
证明:如图,在ON上取一点P,使得OP=OA,连接AP,
∵∠AOP=60°,点B与点D关于OM对称,
∴△AOP是等边三角形,∠AOD=60°,
∴∠OAP=∠APO=∠AOD=60°,AP=AO.
∵∠OAP=∠DAC=60°,∴∠DAO=∠CAP.
在△ADO和△ACP中,
∴△ADO≌△ACP(ASA),
∴OD=PC,∴OA=OP=PC+OC=OD+OC.
能力提升全练
10.C 根据轴对称图形的概念可知只有选项C中的剪纸图案是轴对称图形.故选C.
11.B ∵直线l是五边形ABCDE的对称轴,∴∠ABE=∠AEB,∠AED=∠ABC=130°,∠D=∠C=100°,
∴∠BAE=540°-130°×2-100°×2=80°,∴∠BEA=×(180°-80°)=50°.
12.C 如图,连接BE,BE与AD交于点P,此时PE+PC最小.
∵△ABC是等边三角形,∴∠BCE=60°,BA=BC.
∵E是AC的中点,∴BE⊥AC,∴∠BEC=90°,
∴∠EBC=30°.
∵△ABC是等边三角形,AD⊥BC,∴BD=CD,
∴AD垂直平分BC,∴BP=CP,∴∠PCB=∠PBC=30°,∴∠CPE=∠PBC+∠PCB=60°.
13.21:05
解析 “”与“”成轴对称,故此时的时间应是21:05.
14.33°
解析 ∵AC=BC,∴∠A=∠B=38°,
∵B'D∥AC,∴∠ADB'=∠A=38°,
∵点B关于直线CD的对称点为B',
∴∠CDB'=∠CDB=×(38°+180°)=109°,
∴∠BCD=180°-38°-109°=33°.
15.a+8b
解析 由题图可得,拼出来的图形的总长度=9a-8(a-b)=a+8b.
16.解析 如图所示.(答案不唯一)
素养探究全练
17.D 分别在∠O的两边上找点A、B,使△PAB的周长最小的是D选项.
18.解析 (1)补全图形后如图①所示,AC与CD的数量关系为AC=CD.
理由:如图①,连接CP,设AB交CD于O,
∵A,P关于直线BC对称,∴CP=CA,∠P=∠A,∠CBP=∠ABC=45°,
∴∠ABP=90°,∴∠ABD=90°,
∵AC⊥CD,∴∠ACO=90°,∴∠ACO=∠DBO,
∵∠AOC=∠DOB,∴∠D=∠A,
∵∠P=∠A,∴∠D=∠P,∴CD=CP,∴AC=CD.
(2)补全图形后如图②所示,AC与CD的数量关系仍为AC=CD.理由:如图②,连接CP,
∵A,P关于直线BC对称,
∴CP=CA,∠P=∠A,∠CBP=∠ABC=45°,
∴∠ABP=90°,
∵AC⊥CD,∴∠ACD=90°,
∴∠ABD+∠ACD=180°,∴∠A+∠BDC=180°,
∵∠CDP+∠BDC=180°,∴∠A=∠CDP,
∵∠P=∠A,∴∠CDP=∠P,∴CD=CP,∴AC=CD.
图① 图②
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
