2022—2023学年人教版数学九年级上册24.3正多边形和圆 同步练习(含答案)
文档属性
| 名称 | 2022—2023学年人教版数学九年级上册24.3正多边形和圆 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 705.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-25 16:22:46 | ||
图片预览


文档简介
24.3 正多边形和圆
班级: 姓名: 成绩:
一、选择题
1.若一个正多边形的中心角为40°,则这个多边形的边数是( )
A.9 B.8 C.7 D.6
2.⊙O半径为4,以⊙O的内接正三角形、正方形、正六边形的边心距为边作一个三角形,则所得三角形的面积是( )
A. B. C.2 D.2
3.如图所示的图案,其外轮廓是一个正五边形,绕它的中心旋转一定的角度后能够与自身重合,则这个旋转角可能是( )
A. B. C. D.
4.平凉市崆峒山塔群是研究院东地区砖石建筑艺术的宝贵实物资料,图①是位于崆峒山灵龟台西的灵秘塔,塔为石基砖砌身,呈六角六面四级阶状尖顶塔,图②是灵秘塔某层的平面示意图,若将其抽象为正六边形,则a的度数为( )
A.45° B.50° C.60° D.72°
5.如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1,则边心距OM的长为________.
A. B. C. D.
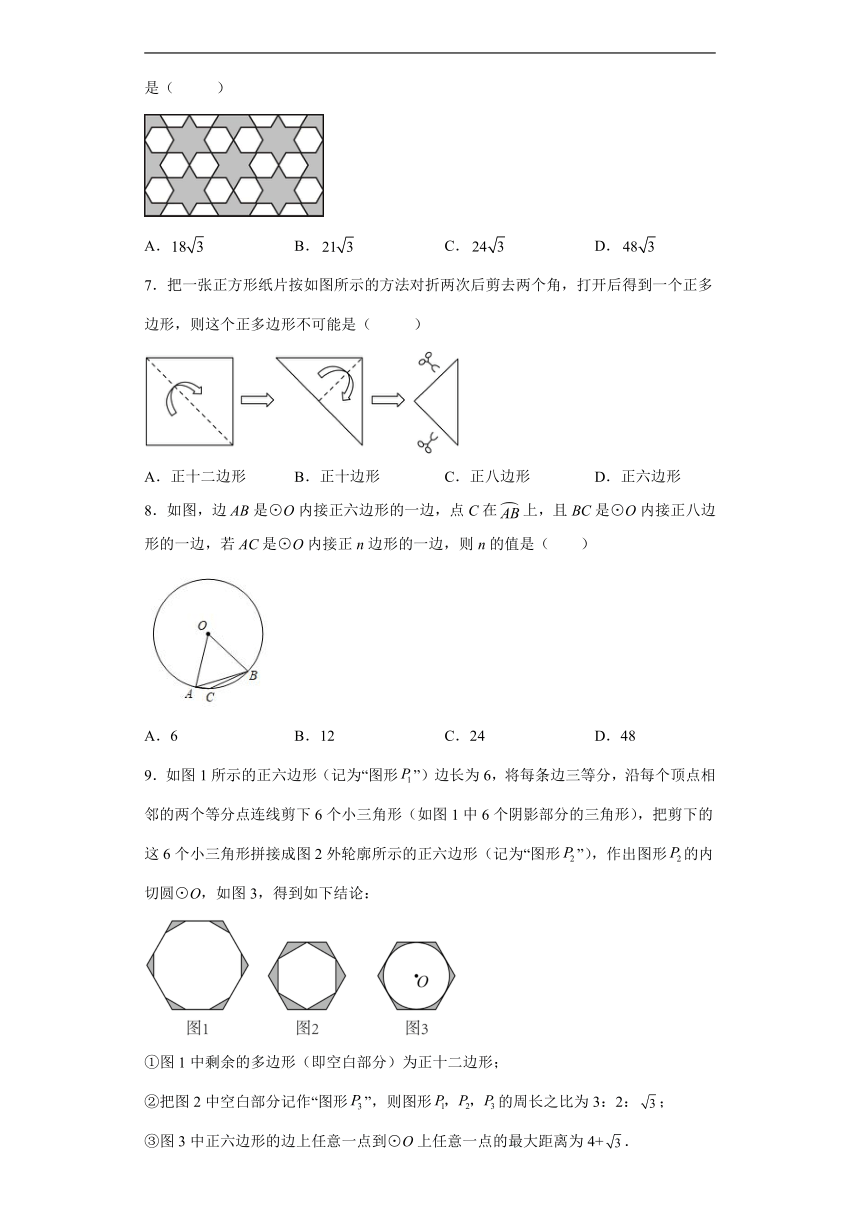
6.如图,是由边长为1的正六边形和六角星镶嵌而成的图案,则图中阴影部分的面积是( )
A. B. C. D.
7.把一张正方形纸片按如图所示的方法对折两次后剪去两个角,打开后得到一个正多边形,则这个正多边形不可能是( )
A.正十二边形 B.正十边形 C.正八边形 D.正六边形
8.如图,边AB是⊙O内接正六边形的一边,点C在上,且BC是⊙O内接正八边形的一边,若AC是⊙O内接正n边形的一边,则n的值是( )
A.6 B.12 C.24 D.48
9.如图1所示的正六边形(记为“图形”)边长为6,将每条边三等分,沿每个顶点相邻的两个等分点连线剪下6个小三角形(如图1中6个阴影部分的三角形),把剪下的这6个小三角形拼接成图2外轮廓所示的正六边形(记为“图形”),作出图形的内切圆⊙O,如图3,得到如下结论:
①图1中剩余的多边形(即空白部分)为正十二边形;
②把图2中空白部分记作“图形”,则图形的周长之比为3:2:;
③图3中正六边形的边上任意一点到⊙O上任意一点的最大距离为4+.
以上结论正确的是( )
A.②③ B.①③ C.② D.①
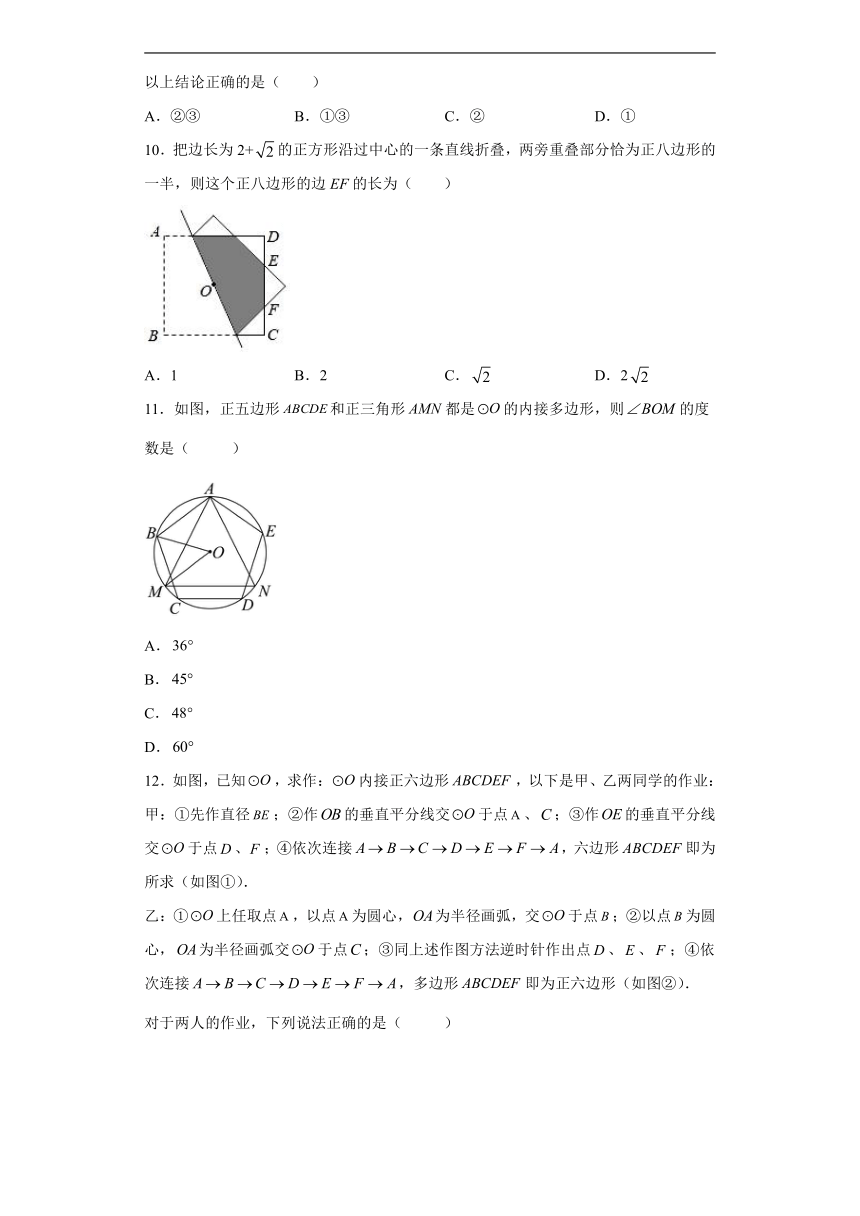
10.把边长为2+的正方形沿过中心的一条直线折叠,两旁重叠部分恰为正八边形的一半,则这个正八边形的边EF的长为( )
A.1 B.2 C. D.2
11.如图,正五边形和正三角形都是的内接多边形,则的度数是( )
A.
B.
C.
D.
12.如图,已知,求作:内接正六边形,以下是甲、乙两同学的作业:
甲:①先作直径;②作的垂直平分线交于点、;③作的垂直平分线交于点、;④依次连接,六边形即为所求(如图①).
乙:①上任取点,以点为圆心,为半径画弧,交于点;②以点为圆心,为半径画弧交于点;③同上述作图方法逆时针作出点、、;④依次连接,多边形即为正六边形(如图②).
对于两人的作业,下列说法正确的是( )
A.两人都不对 B.甲对,乙不对 C.两人都对 D.甲不对,乙对
二、填空题
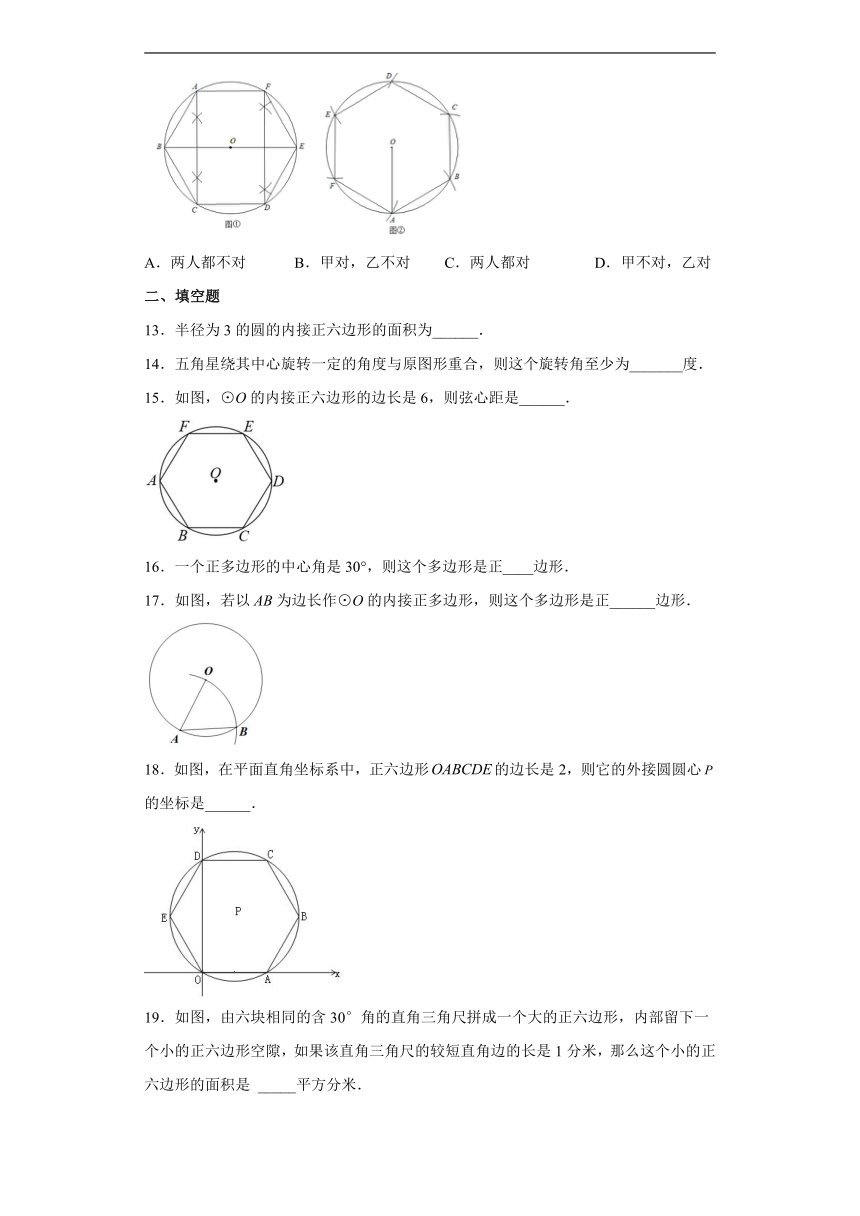
13.半径为3的圆的内接正六边形的面积为______.
14.五角星绕其中心旋转一定的角度与原图形重合,则这个旋转角至少为_______度.
15.如图,⊙O的内接正六边形的边长是6,则弦心距是______.
16.一个正多边形的中心角是30°,则这个多边形是正____边形.
17.如图,若以AB为边长作⊙O的内接正多边形,则这个多边形是正______边形.
18.如图,在平面直角坐标系中,正六边形的边长是2,则它的外接圆圆心的坐标是______.
19.如图,由六块相同的含30°角的直角三角尺拼成一个大的正六边形,内部留下一个小的正六边形空隙,如果该直角三角尺的较短直角边的长是1分米,那么这个小的正六边形的面积是 _____平方分米.
20.如图,在每个小正方形的边长为1的网格中,O为格点,⊙经过格点A.
(1)⊙的周长等于____;
(2)请用无刻度的直尺,在如图所示的网格中,画出⊙的内接等边,并简要说明点B,C的位置是如何找到的(不要求证明)_____.
三、解答题
21.如图,点是正方形,的中心.
(1)用直尺和圆规在正方形内部作一点(异于点),使得(保留作图痕迹,不写作法)
(2)连接求证:.
22.如图,正方形内接于,为上的一点,连接,.
(1)求的度数;
(2)当点为的中点时,是的内接正边形的一边,求的值.
23.如图所示,正三角形ABC、正方形ABCD、正五边形ABCDE分别是的内接三角形、内接四边形、内接五边形,点M、N分别从点B、C开始,以相同的速度在上逆时针运动.
(1)求图①中的度数
(2)图②中的度数是______,图③中的度数是______;
(3)若推广到一般的正n边形情况,请写出的度数是______.
试卷第1页,共3页
参考答案
1.A
2.C
3.B
4.C
5.B
6.C
7.B
8.C
9.A
10.C
11.C
12.C
13.
14.72
15.
16.十二
17.六
18..
19.
20.(1)∵⊙的半径为:,
∴⊙的周长,
(2)如图:∵,
又∵,
∴,
∴.
∵,
∴,
∴.
∵,
∴.
∵,
∴.
∴,
∵,
∴四边形是平行四边形,
∵,
∴是矩形.
∴,
∴,
∵,
∴,
∴,
∴.
∵,
∴,
∵过圆心, ,
∴,
∴,
∴,
∵,
∴是等边三角形.
21.如图所示,点即为所求.
连接
由得:
是正方形中心,
在和中,
.
22.解:(1)连接,,
∵正方形内接于,
∴.
∴;
(2)连接,,
∵正方形内接于,
∴.
∵点为的中点,
∴,
∴∠COP=∠BOP,
∵∠COP+∠BOP=∠COB=90°,
∴,
∴.
23.解:(1)∵是正三角形,
∴,
∵点M、N分别从点B、C开始以相同的速度在上逆时针运动,
∴,
∴,
∴;
(2)由图②,四边形ABCD是正方形,则与(1)同理,
,
∴;
由图③,正五边形ABCDE中,与(1)同理,
∴,
∴;
(3)由(1)可知,∠APB为所在正多边形的外角度数,故在图n中,有∠APB=;
班级: 姓名: 成绩:
一、选择题
1.若一个正多边形的中心角为40°,则这个多边形的边数是( )
A.9 B.8 C.7 D.6
2.⊙O半径为4,以⊙O的内接正三角形、正方形、正六边形的边心距为边作一个三角形,则所得三角形的面积是( )
A. B. C.2 D.2
3.如图所示的图案,其外轮廓是一个正五边形,绕它的中心旋转一定的角度后能够与自身重合,则这个旋转角可能是( )
A. B. C. D.
4.平凉市崆峒山塔群是研究院东地区砖石建筑艺术的宝贵实物资料,图①是位于崆峒山灵龟台西的灵秘塔,塔为石基砖砌身,呈六角六面四级阶状尖顶塔,图②是灵秘塔某层的平面示意图,若将其抽象为正六边形,则a的度数为( )
A.45° B.50° C.60° D.72°
5.如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1,则边心距OM的长为________.
A. B. C. D.
6.如图,是由边长为1的正六边形和六角星镶嵌而成的图案,则图中阴影部分的面积是( )
A. B. C. D.
7.把一张正方形纸片按如图所示的方法对折两次后剪去两个角,打开后得到一个正多边形,则这个正多边形不可能是( )
A.正十二边形 B.正十边形 C.正八边形 D.正六边形
8.如图,边AB是⊙O内接正六边形的一边,点C在上,且BC是⊙O内接正八边形的一边,若AC是⊙O内接正n边形的一边,则n的值是( )
A.6 B.12 C.24 D.48
9.如图1所示的正六边形(记为“图形”)边长为6,将每条边三等分,沿每个顶点相邻的两个等分点连线剪下6个小三角形(如图1中6个阴影部分的三角形),把剪下的这6个小三角形拼接成图2外轮廓所示的正六边形(记为“图形”),作出图形的内切圆⊙O,如图3,得到如下结论:
①图1中剩余的多边形(即空白部分)为正十二边形;
②把图2中空白部分记作“图形”,则图形的周长之比为3:2:;
③图3中正六边形的边上任意一点到⊙O上任意一点的最大距离为4+.
以上结论正确的是( )
A.②③ B.①③ C.② D.①
10.把边长为2+的正方形沿过中心的一条直线折叠,两旁重叠部分恰为正八边形的一半,则这个正八边形的边EF的长为( )
A.1 B.2 C. D.2
11.如图,正五边形和正三角形都是的内接多边形,则的度数是( )
A.
B.
C.
D.
12.如图,已知,求作:内接正六边形,以下是甲、乙两同学的作业:
甲:①先作直径;②作的垂直平分线交于点、;③作的垂直平分线交于点、;④依次连接,六边形即为所求(如图①).
乙:①上任取点,以点为圆心,为半径画弧,交于点;②以点为圆心,为半径画弧交于点;③同上述作图方法逆时针作出点、、;④依次连接,多边形即为正六边形(如图②).
对于两人的作业,下列说法正确的是( )
A.两人都不对 B.甲对,乙不对 C.两人都对 D.甲不对,乙对
二、填空题
13.半径为3的圆的内接正六边形的面积为______.
14.五角星绕其中心旋转一定的角度与原图形重合,则这个旋转角至少为_______度.
15.如图,⊙O的内接正六边形的边长是6,则弦心距是______.
16.一个正多边形的中心角是30°,则这个多边形是正____边形.
17.如图,若以AB为边长作⊙O的内接正多边形,则这个多边形是正______边形.
18.如图,在平面直角坐标系中,正六边形的边长是2,则它的外接圆圆心的坐标是______.
19.如图,由六块相同的含30°角的直角三角尺拼成一个大的正六边形,内部留下一个小的正六边形空隙,如果该直角三角尺的较短直角边的长是1分米,那么这个小的正六边形的面积是 _____平方分米.
20.如图,在每个小正方形的边长为1的网格中,O为格点,⊙经过格点A.
(1)⊙的周长等于____;
(2)请用无刻度的直尺,在如图所示的网格中,画出⊙的内接等边,并简要说明点B,C的位置是如何找到的(不要求证明)_____.
三、解答题
21.如图,点是正方形,的中心.
(1)用直尺和圆规在正方形内部作一点(异于点),使得(保留作图痕迹,不写作法)
(2)连接求证:.
22.如图,正方形内接于,为上的一点,连接,.
(1)求的度数;
(2)当点为的中点时,是的内接正边形的一边,求的值.
23.如图所示,正三角形ABC、正方形ABCD、正五边形ABCDE分别是的内接三角形、内接四边形、内接五边形,点M、N分别从点B、C开始,以相同的速度在上逆时针运动.
(1)求图①中的度数
(2)图②中的度数是______,图③中的度数是______;
(3)若推广到一般的正n边形情况,请写出的度数是______.
试卷第1页,共3页
参考答案
1.A
2.C
3.B
4.C
5.B
6.C
7.B
8.C
9.A
10.C
11.C
12.C
13.
14.72
15.
16.十二
17.六
18..
19.
20.(1)∵⊙的半径为:,
∴⊙的周长,
(2)如图:∵,
又∵,
∴,
∴.
∵,
∴,
∴.
∵,
∴.
∵,
∴.
∴,
∵,
∴四边形是平行四边形,
∵,
∴是矩形.
∴,
∴,
∵,
∴,
∴,
∴.
∵,
∴,
∵过圆心, ,
∴,
∴,
∴,
∵,
∴是等边三角形.
21.如图所示,点即为所求.
连接
由得:
是正方形中心,
在和中,
.
22.解:(1)连接,,
∵正方形内接于,
∴.
∴;
(2)连接,,
∵正方形内接于,
∴.
∵点为的中点,
∴,
∴∠COP=∠BOP,
∵∠COP+∠BOP=∠COB=90°,
∴,
∴.
23.解:(1)∵是正三角形,
∴,
∵点M、N分别从点B、C开始以相同的速度在上逆时针运动,
∴,
∴,
∴;
(2)由图②,四边形ABCD是正方形,则与(1)同理,
,
∴;
由图③,正五边形ABCDE中,与(1)同理,
∴,
∴;
(3)由(1)可知,∠APB为所在正多边形的外角度数,故在图n中,有∠APB=;
同课章节目录
