2022—2023学年人教版数学九年级上册24.4弧长和扇形面积同步练习(含答案)
文档属性
| 名称 | 2022—2023学年人教版数学九年级上册24.4弧长和扇形面积同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 585.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-25 16:57:36 | ||
图片预览


文档简介
24.4 弧长和扇形面积
班级: 姓名: 成绩:
一、选择题
1.已知,如图,⊙O的半径为6,正六边形ABCDEF与⊙O相切于点C、F,则的长度是( )
A.2π B.3π C.4π D.5π
2.用一个圆心角为,半径为6的扇形做一个圆锥的侧面,则这个圆锥的底面圆的面积为( ).
A. B. C. D.
3.实验学校的花坛形状如图所示,其中,等圆⊙O1与⊙O2的半径为3米,且⊙O1经过⊙O2的圆心O2.已知实线部分为此花坛的周长,则花坛的周长为( )
A.4π米 B.6π米 C.8π米 D.12π米
4.如图,在4×4的正方形网格中,若将△ABC绕着点A逆时针旋转得到△,则 的长为( )
A. B. C.7 D.6
5.分别以等边三角形的每个顶点为圆心,以边长为半径,在另两个顶点间画一段圆弧,三段圆弧围成的曲边三角形称为勒洛三角形.若等边三角形的边长为4,则勒洛三角形的周长为( )
A. B. C. D.
6.如图所示,圆锥形烟囱帽的底面半径为,侧面展开图为半圆形,则它的母线长为( )
A. B. C. D.
7.75°的圆心角所对的弧长是2.5πcm,则此弧所在圆的半径是( )
A.6cm B.7cm C.8cm D.9cm
8.用一块圆心角为120°的扇形铁皮,围成一个底面直径为10cm的圆锥形工件的侧面,那么这个圆锥的高是( )
A.12cm B.cm C.15cm D.30cm
9.如图,在矩形ABCD中,已知,,矩形在直线l上绕其右下角的顶点B向右旋转至图①位置,再绕右下角的顶点继续向右旋转至图②位置,…,以此类推,这样连续旋转2021次后,顶点A在整个旋转过程中所经过的路程之和是( )
A. B. C. D.
10.如图是边长为1的正方形组成的网格,△ABC的顶点都在格点上,将△ABC绕点C逆时针旋转60°,则顶点B所经过的路径长为( )
A. B. C. D.
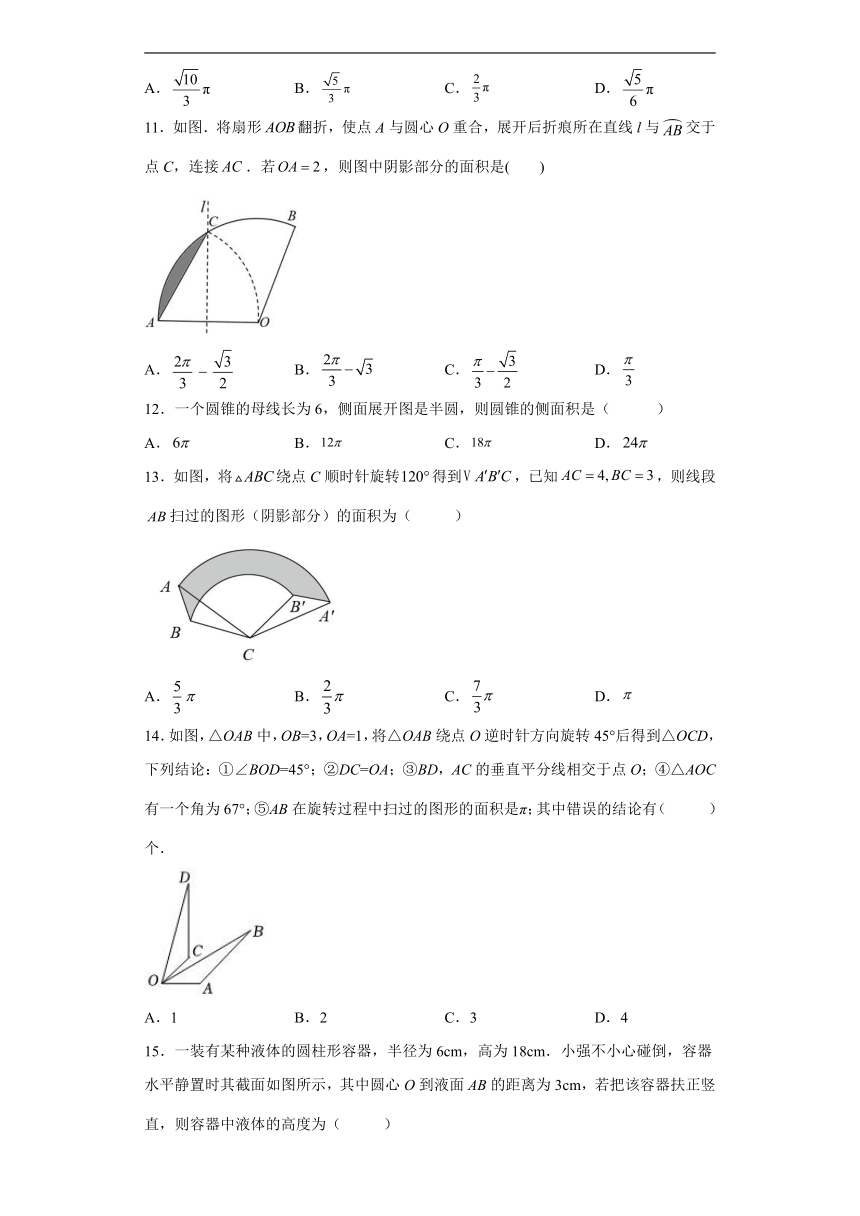
11.如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接.若,则图中阴影部分的面积是( )
A. B. C. D.
12.一个圆锥的母线长为6,侧面展开图是半圆,则圆锥的侧面积是( )
A. B. C. D.
13.如图,将绕点C顺时针旋转得到,已知,则线段扫过的图形(阴影部分)的面积为( )
A. B. C. D.
14.如图,△OAB中,OB=3,OA=1,将△OAB绕点O逆时针方向旋转45°后得到△OCD,下列结论:①∠BOD=45°;②DC=OA;③BD,AC的垂直平分线相交于点O;④△AOC有一个角为67°;⑤AB在旋转过程中扫过的图形的面积是π;其中错误的结论有( )个.
A.1 B.2 C.3 D.4
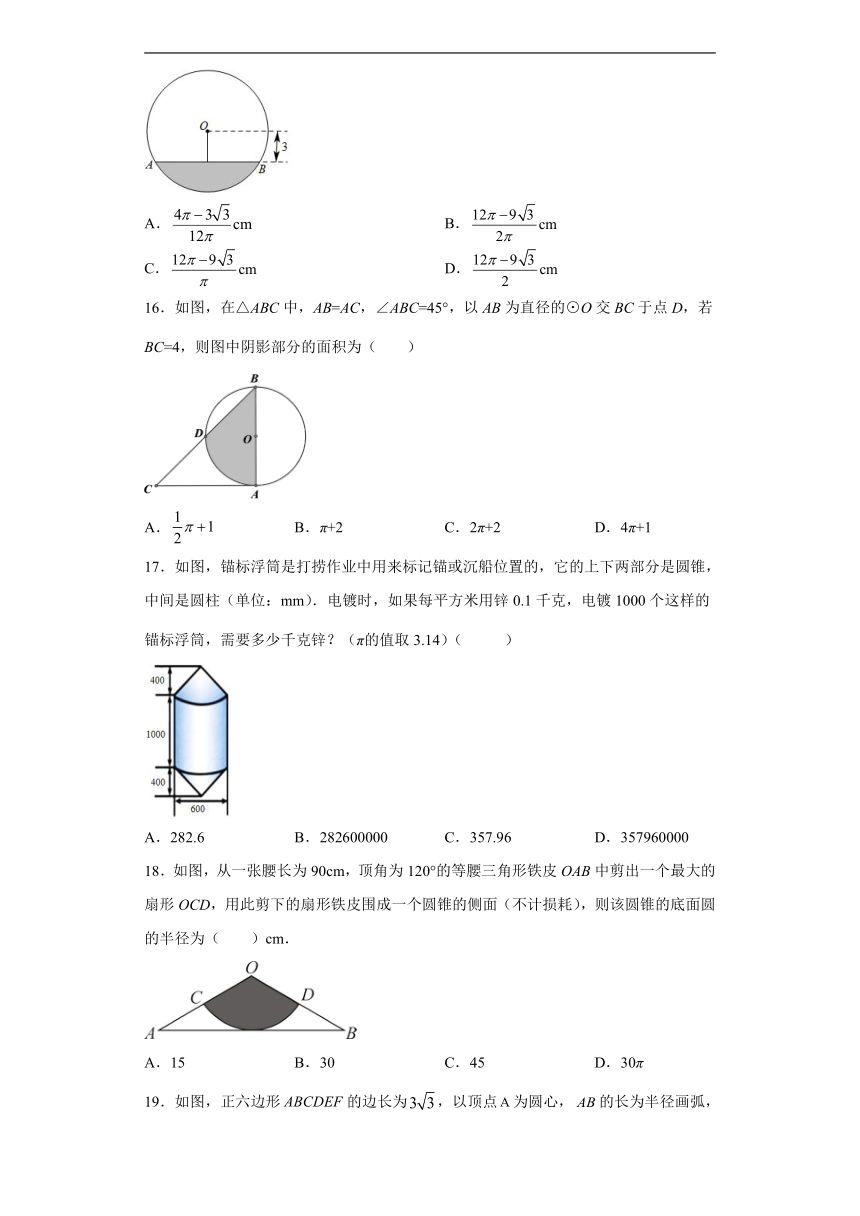
15.一装有某种液体的圆柱形容器,半径为6cm,高为18cm.小强不小心碰倒,容器水平静置时其截面如图所示,其中圆心O到液面AB的距离为3cm,若把该容器扶正竖直,则容器中液体的高度为( )
A. B.
C. D.
16.如图,在△ABC中,AB=AC,∠ABC=45°,以AB为直径的⊙O交BC于点D,若BC=4,则图中阴影部分的面积为( )
A. B.π+2 C.2π+2 D.4π+1
17.如图,锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是圆柱(单位:mm).电镀时,如果每平方米用锌0.1千克,电镀1000个这样的锚标浮筒,需要多少千克锌?(π的值取3.14)( )
A.282.6 B.282600000 C.357.96 D.357960000
18.如图,从一张腰长为90cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面圆的半径为( )cm.
A.15 B.30 C.45 D.30π
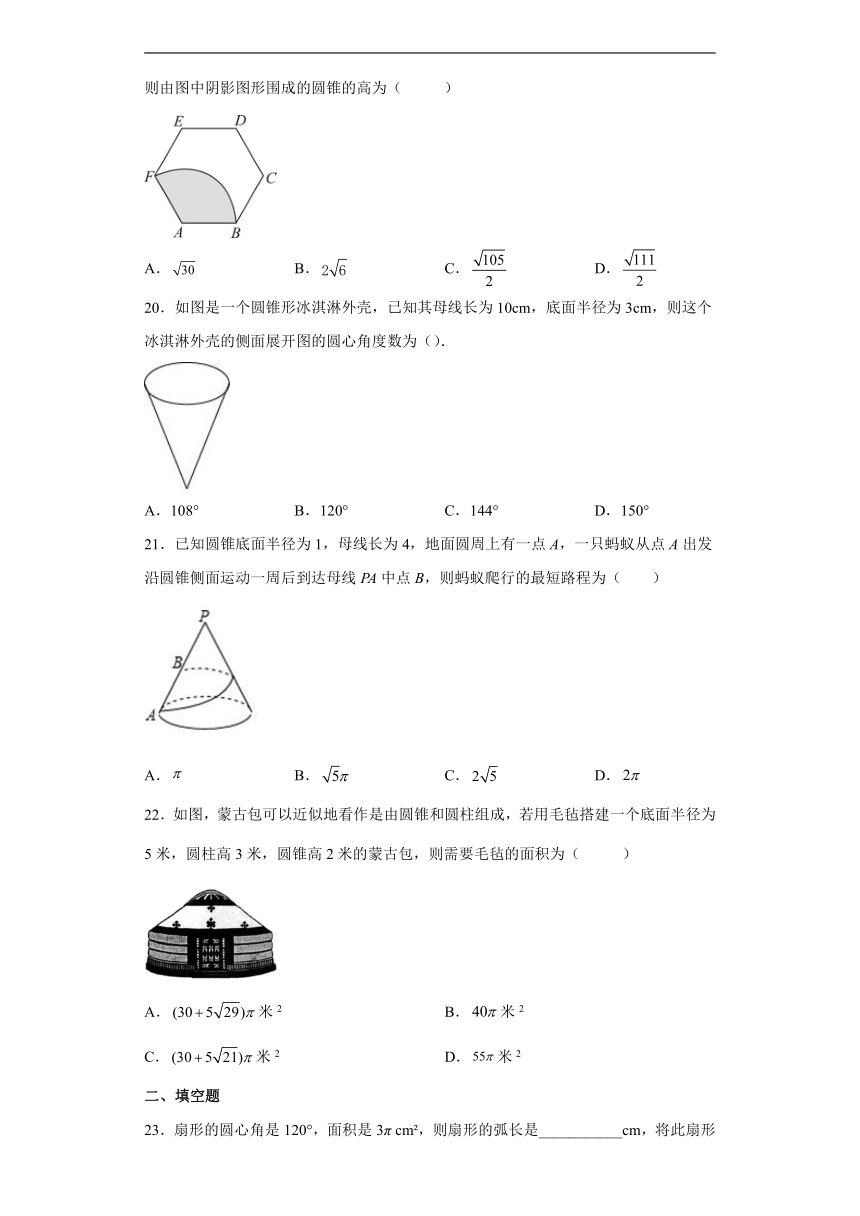
19.如图,正六边形的边长为,以顶点为圆心,的长为半径画弧,则由图中阴影图形围成的圆锥的高为( )
A. B. C. D.
20.如图是一个圆锥形冰淇淋外壳,已知其母线长为10cm,底面半径为3cm,则这个冰淇淋外壳的侧面展开图的圆心角度数为().
A.108° B.120° C.144° D.150°
21.已知圆锥底面半径为1,母线长为4,地面圆周上有一点A,一只蚂蚁从点A出发沿圆锥侧面运动一周后到达母线PA中点B,则蚂蚁爬行的最短路程为( )
A. B. C. D.
22.如图,蒙古包可以近似地看作是由圆锥和圆柱组成,若用毛毡搭建一个底面半径为5米,圆柱高3米,圆锥高2米的蒙古包,则需要毛毡的面积为( )
A.米2 B.米2
C.米2 D.米2
二、填空题
23.扇形的圆心角是120°,面积是3π cm ,则扇形的弧长是___________cm,将此扇形卷成一个圆锥,则底面圆的半径为_________cm.
24.一个扇形的圆心角为60°,它所对的弧长为2πcm,则这个扇形所在圆的周长为____________cm.
25.若圆锥底面的半径为3,它的侧面展开图的面积为,则它的母线长为_______.
26.如图,弧长为半圆的弓形在坐标系中,圆心在.将弓形沿轴正方向无滑动滚动,当圆心经过的路径长为时,圆心的坐标是______.
27.如图,在扇形OAB中,,,以点A为圆心,AO长为半径圆弧,交AB于点D,则图中阴影部分图形的面积是_________.
28.如图,已知⊙O的半径为2,△ABC内接于⊙O,∠ACB=135°,则AB=_____,弓形ACB的面积为_____.
29.已知一个圆锥的底面半径为2cm,母线长为5cm,则这个圆锥的全面积是___cm2.
30.如图,从一块直径是m的圆形铁皮上剪出一个圆心角为90°的扇形,将其围成一个圆锥,圆锥底面圆的半径是__________m.
三、解答题
31.如图,AB为⊙O的直径,C为⊙O上一点,弦AE的延长线与过点C的切线互相垂直,垂足为D,∠CAD=33°,连接BC.
(1)求∠B的度数.
(2)若AB=4,求的长.
32.如图,有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC.
(1)求剪下的扇形ABC(即阴影部分)的半径;
(2)若用此剪下的扇形铁皮围成一个圆锥形铁帽,求此圆锥形铁帽的底面圆的半径r.
33.如图,在平面直角坐标系中,Rt△ABC三个顶点都在格点上,点A、B、C的坐标分别为A(﹣4,1),B(﹣1,1),C(﹣1,3).请解答下列问题:
(1)画出△ABC关于原点O的中心对称图形△A1B1C1,并写出点C的对应点C1的坐标;
(2)画出△ABC绕原点O逆时针旋转90°后得到的△A2B2C2,并直接写出点A旋转至A2经过的路径长.
34.在如图①所示的方格纸中,每个小方格都是边长为1个单位长度的正方形,a,b,c均为顶点都在格点上的三角形(每个小方格的顶点叫做格点).
(1)在图①中,a经过一次 变换(填“平移”“旋转”或“轴对称”)可以得到b;
(2)在图①中,c是可以由b经过一次旋转变换得到的,其旋转中心是点 (填“A”“B”或“C”);
(3)在图②中画出a绕点A顺时针旋转90°后得到的d,并求出线段EF所扫过的面积.
试卷第1页,共3页
参考答案
1.C
2.D
3.C
4.A
5.D
6.D
7.A
8.B
9.D
10.B
11.B
12.C
13.C
14.A
15.B
16.A
17.A
18.A
19.B
20.A
21.C
22.A
23.2π 1
24.12π
25.##
26.
27.
28. π-2##
29.
30.
31.(1)解:如图,连接OC,
∵CD与⊙O相切于点C,
∴OC⊥CD,
又∵AD⊥CD,
∴ADOC,
∴∠1=∠3=33°,
又∵OA=OC,
∴∠2=∠3=33°,
∵AB为直径,
∴∠ACB=90°,
∴∠B=90°-33°=57°;
(2)连接OE,
∵∠CAD=33°,
∴∠EOC=2∠CAD=66°,
∵AB=4,
∴OE=2,
∴的长为:.
32.(1)解:连接OA,OB,OC,作OD⊥AB于点D.
则AD=AB,
∵BA= CA,OA= OA,OB= OC,
∴△BAO≌△CAO,
∴∠BAO=∠CAO,
∵∠BAC=60°,
∴∠BAO=30 °,
∵圆的直径为4,
∴ OA=2,
∴OD=1,DA==,
∴AB=2DA=2;
∴剪下的扇形ABC(即阴影部分)的半径为2;
(2)解:则扇形(即阴影部分)的弧长是:,
根据题意得:,
解得:r=.
答:此圆锥形铁帽的底面圆的半径为.
33.(1)解:△ABC关于原点O的中心对称图形△A1B1C1如图所示:
点C1的坐标为(1,3).
(2)解:△ABC绕原点O逆时针旋转90°后得到的△A2B2C2,如(1)图所示:
∵OA=,
∴点A经过的路径长为:.
34.(1)解:在图①中,a先向上平移1个单位,再向右平移3个单位得到b,
则a经过一次平移变换得到b,
故答案为:平移.
(2)在图①中,b绕着A点旋转后可以得到c,则c是可以由b经过一次旋转变换得到的,其旋转中心是A点
(3)在图②中,图形d即为所求,
EF扫过的面积.
班级: 姓名: 成绩:
一、选择题
1.已知,如图,⊙O的半径为6,正六边形ABCDEF与⊙O相切于点C、F,则的长度是( )
A.2π B.3π C.4π D.5π
2.用一个圆心角为,半径为6的扇形做一个圆锥的侧面,则这个圆锥的底面圆的面积为( ).
A. B. C. D.
3.实验学校的花坛形状如图所示,其中,等圆⊙O1与⊙O2的半径为3米,且⊙O1经过⊙O2的圆心O2.已知实线部分为此花坛的周长,则花坛的周长为( )
A.4π米 B.6π米 C.8π米 D.12π米
4.如图,在4×4的正方形网格中,若将△ABC绕着点A逆时针旋转得到△,则 的长为( )
A. B. C.7 D.6
5.分别以等边三角形的每个顶点为圆心,以边长为半径,在另两个顶点间画一段圆弧,三段圆弧围成的曲边三角形称为勒洛三角形.若等边三角形的边长为4,则勒洛三角形的周长为( )
A. B. C. D.
6.如图所示,圆锥形烟囱帽的底面半径为,侧面展开图为半圆形,则它的母线长为( )
A. B. C. D.
7.75°的圆心角所对的弧长是2.5πcm,则此弧所在圆的半径是( )
A.6cm B.7cm C.8cm D.9cm
8.用一块圆心角为120°的扇形铁皮,围成一个底面直径为10cm的圆锥形工件的侧面,那么这个圆锥的高是( )
A.12cm B.cm C.15cm D.30cm
9.如图,在矩形ABCD中,已知,,矩形在直线l上绕其右下角的顶点B向右旋转至图①位置,再绕右下角的顶点继续向右旋转至图②位置,…,以此类推,这样连续旋转2021次后,顶点A在整个旋转过程中所经过的路程之和是( )
A. B. C. D.
10.如图是边长为1的正方形组成的网格,△ABC的顶点都在格点上,将△ABC绕点C逆时针旋转60°,则顶点B所经过的路径长为( )
A. B. C. D.
11.如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接.若,则图中阴影部分的面积是( )
A. B. C. D.
12.一个圆锥的母线长为6,侧面展开图是半圆,则圆锥的侧面积是( )
A. B. C. D.
13.如图,将绕点C顺时针旋转得到,已知,则线段扫过的图形(阴影部分)的面积为( )
A. B. C. D.
14.如图,△OAB中,OB=3,OA=1,将△OAB绕点O逆时针方向旋转45°后得到△OCD,下列结论:①∠BOD=45°;②DC=OA;③BD,AC的垂直平分线相交于点O;④△AOC有一个角为67°;⑤AB在旋转过程中扫过的图形的面积是π;其中错误的结论有( )个.
A.1 B.2 C.3 D.4
15.一装有某种液体的圆柱形容器,半径为6cm,高为18cm.小强不小心碰倒,容器水平静置时其截面如图所示,其中圆心O到液面AB的距离为3cm,若把该容器扶正竖直,则容器中液体的高度为( )
A. B.
C. D.
16.如图,在△ABC中,AB=AC,∠ABC=45°,以AB为直径的⊙O交BC于点D,若BC=4,则图中阴影部分的面积为( )
A. B.π+2 C.2π+2 D.4π+1
17.如图,锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是圆柱(单位:mm).电镀时,如果每平方米用锌0.1千克,电镀1000个这样的锚标浮筒,需要多少千克锌?(π的值取3.14)( )
A.282.6 B.282600000 C.357.96 D.357960000
18.如图,从一张腰长为90cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面圆的半径为( )cm.
A.15 B.30 C.45 D.30π
19.如图,正六边形的边长为,以顶点为圆心,的长为半径画弧,则由图中阴影图形围成的圆锥的高为( )
A. B. C. D.
20.如图是一个圆锥形冰淇淋外壳,已知其母线长为10cm,底面半径为3cm,则这个冰淇淋外壳的侧面展开图的圆心角度数为().
A.108° B.120° C.144° D.150°
21.已知圆锥底面半径为1,母线长为4,地面圆周上有一点A,一只蚂蚁从点A出发沿圆锥侧面运动一周后到达母线PA中点B,则蚂蚁爬行的最短路程为( )
A. B. C. D.
22.如图,蒙古包可以近似地看作是由圆锥和圆柱组成,若用毛毡搭建一个底面半径为5米,圆柱高3米,圆锥高2米的蒙古包,则需要毛毡的面积为( )
A.米2 B.米2
C.米2 D.米2
二、填空题
23.扇形的圆心角是120°,面积是3π cm ,则扇形的弧长是___________cm,将此扇形卷成一个圆锥,则底面圆的半径为_________cm.
24.一个扇形的圆心角为60°,它所对的弧长为2πcm,则这个扇形所在圆的周长为____________cm.
25.若圆锥底面的半径为3,它的侧面展开图的面积为,则它的母线长为_______.
26.如图,弧长为半圆的弓形在坐标系中,圆心在.将弓形沿轴正方向无滑动滚动,当圆心经过的路径长为时,圆心的坐标是______.
27.如图,在扇形OAB中,,,以点A为圆心,AO长为半径圆弧,交AB于点D,则图中阴影部分图形的面积是_________.
28.如图,已知⊙O的半径为2,△ABC内接于⊙O,∠ACB=135°,则AB=_____,弓形ACB的面积为_____.
29.已知一个圆锥的底面半径为2cm,母线长为5cm,则这个圆锥的全面积是___cm2.
30.如图,从一块直径是m的圆形铁皮上剪出一个圆心角为90°的扇形,将其围成一个圆锥,圆锥底面圆的半径是__________m.
三、解答题
31.如图,AB为⊙O的直径,C为⊙O上一点,弦AE的延长线与过点C的切线互相垂直,垂足为D,∠CAD=33°,连接BC.
(1)求∠B的度数.
(2)若AB=4,求的长.
32.如图,有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC.
(1)求剪下的扇形ABC(即阴影部分)的半径;
(2)若用此剪下的扇形铁皮围成一个圆锥形铁帽,求此圆锥形铁帽的底面圆的半径r.
33.如图,在平面直角坐标系中,Rt△ABC三个顶点都在格点上,点A、B、C的坐标分别为A(﹣4,1),B(﹣1,1),C(﹣1,3).请解答下列问题:
(1)画出△ABC关于原点O的中心对称图形△A1B1C1,并写出点C的对应点C1的坐标;
(2)画出△ABC绕原点O逆时针旋转90°后得到的△A2B2C2,并直接写出点A旋转至A2经过的路径长.
34.在如图①所示的方格纸中,每个小方格都是边长为1个单位长度的正方形,a,b,c均为顶点都在格点上的三角形(每个小方格的顶点叫做格点).
(1)在图①中,a经过一次 变换(填“平移”“旋转”或“轴对称”)可以得到b;
(2)在图①中,c是可以由b经过一次旋转变换得到的,其旋转中心是点 (填“A”“B”或“C”);
(3)在图②中画出a绕点A顺时针旋转90°后得到的d,并求出线段EF所扫过的面积.
试卷第1页,共3页
参考答案
1.C
2.D
3.C
4.A
5.D
6.D
7.A
8.B
9.D
10.B
11.B
12.C
13.C
14.A
15.B
16.A
17.A
18.A
19.B
20.A
21.C
22.A
23.2π 1
24.12π
25.##
26.
27.
28. π-2##
29.
30.
31.(1)解:如图,连接OC,
∵CD与⊙O相切于点C,
∴OC⊥CD,
又∵AD⊥CD,
∴ADOC,
∴∠1=∠3=33°,
又∵OA=OC,
∴∠2=∠3=33°,
∵AB为直径,
∴∠ACB=90°,
∴∠B=90°-33°=57°;
(2)连接OE,
∵∠CAD=33°,
∴∠EOC=2∠CAD=66°,
∵AB=4,
∴OE=2,
∴的长为:.
32.(1)解:连接OA,OB,OC,作OD⊥AB于点D.
则AD=AB,
∵BA= CA,OA= OA,OB= OC,
∴△BAO≌△CAO,
∴∠BAO=∠CAO,
∵∠BAC=60°,
∴∠BAO=30 °,
∵圆的直径为4,
∴ OA=2,
∴OD=1,DA==,
∴AB=2DA=2;
∴剪下的扇形ABC(即阴影部分)的半径为2;
(2)解:则扇形(即阴影部分)的弧长是:,
根据题意得:,
解得:r=.
答:此圆锥形铁帽的底面圆的半径为.
33.(1)解:△ABC关于原点O的中心对称图形△A1B1C1如图所示:
点C1的坐标为(1,3).
(2)解:△ABC绕原点O逆时针旋转90°后得到的△A2B2C2,如(1)图所示:
∵OA=,
∴点A经过的路径长为:.
34.(1)解:在图①中,a先向上平移1个单位,再向右平移3个单位得到b,
则a经过一次平移变换得到b,
故答案为:平移.
(2)在图①中,b绕着A点旋转后可以得到c,则c是可以由b经过一次旋转变换得到的,其旋转中心是A点
(3)在图②中,图形d即为所求,
EF扫过的面积.
同课章节目录
