函数图象

课件38张PPT。函数的图象1.作图
(1)列表描点法
其基本步骤是列表、描点、连线，首先：①确定函数的 ；②化简函数 ；③讨论函数的性质(奇偶性、单调性、周期性、对称性)；其次：列表(尤其注意特殊点、零点、最大值、最小值、与坐标轴的交点)，描点，连线．基础知识梳理定义域解析式(2)图象变换法
1)平移变换
①水平平移：y＝f(x±a)(a>0)的图象，可由y＝f(x)的图象向 (＋)或向右(－)平移 单位而得到．
②竖直平移：y＝f(x)±b(b>0)的图象，可由y＝f(x)的图象向 (＋)或向下(－)平移 单位而得到．基础知识梳理左a个上b个2)对称变换
①y＝f(－x)与y＝f(x)的图象关于 对称．
②y＝－f(x)与y＝f(x)的图象关于 对称．
③y＝－f(－x)与y＝f(x)的图象关于 对称．基础知识梳理y轴x轴原 点 基础知识梳理思考？函数y＝|f(x)|和y＝f(|x|)的图象有何不同？3)伸缩变换
①y＝Af(x)(A>0)的图象，可将y＝f(x)图象上所有点的纵坐标变为原来的A倍， 不变而得到．
②y＝f(ax)(a>0)的图象，可将y＝f(x)图象上所有点的横坐标变为原来的 倍， 不变而得到．基础知识梳理横坐标纵坐标 2．识图
对于给定的函数的图象，要能从
图象的左右、上下分布范围、变化趋势、对称性等方面研究函数的 、
、 、 、 ，
注意图象与函数解析式中参数的关系．基础知识梳理定义域值域单调性奇偶性周期性3．用图
函数图象形象地显示了函数的性质，为研究数量关系提供了“形”的直观性，它是探求解题途径，获得问题结果的重要工具．要重视 解题的思想方法．基础知识梳理数形结合1．一次函数f(x)的图象过点A(0,1)和B(1,2)，则下列各点在函数f(x)的图象上的是(　　)
A．(2,2)　　　　B．(－1,1)
C．(3,2) D．(2,3)
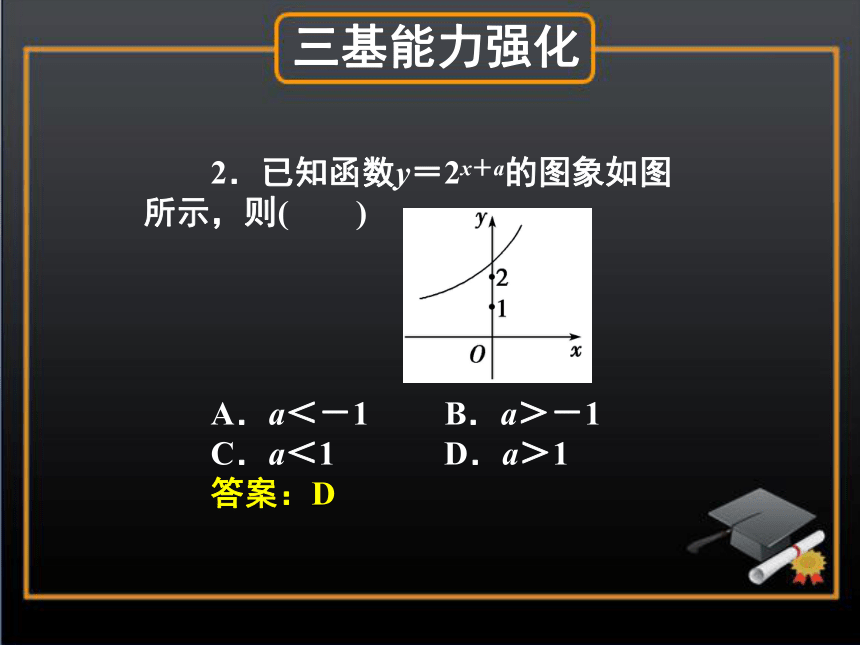
答案：D三基能力强化2．已知函数y＝2x＋a的图象如图所示，则(　　)
A．a＜－1 B．a＞－1
C．a＜1 D．a＞1
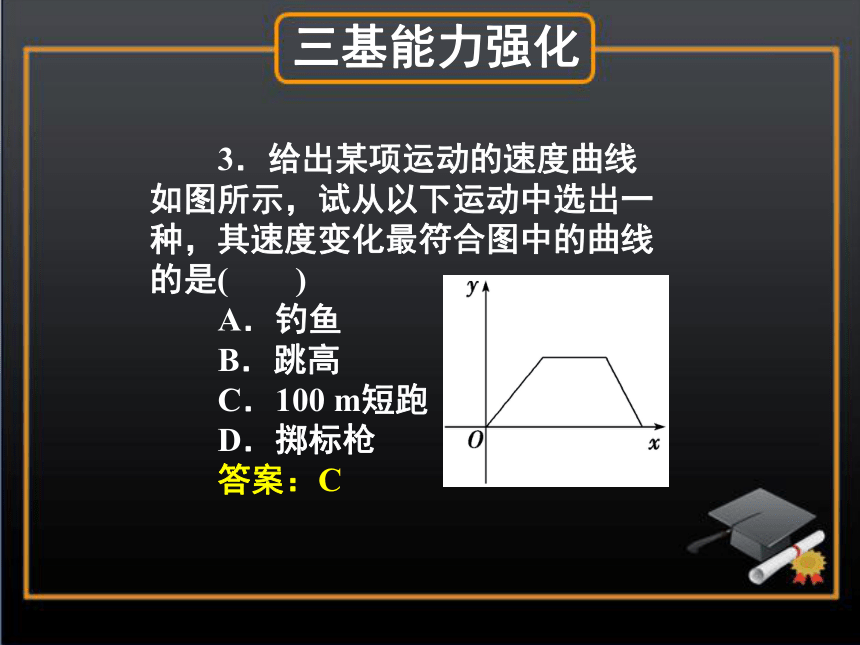
答案：D三基能力强化3．给出某项运动的速度曲线如图所示，试从以下运动中选出一种，其速度变化最符合图中的曲线的是(　　)
A．钓鱼
B．跳高
C．100 m短跑
D．掷标枪
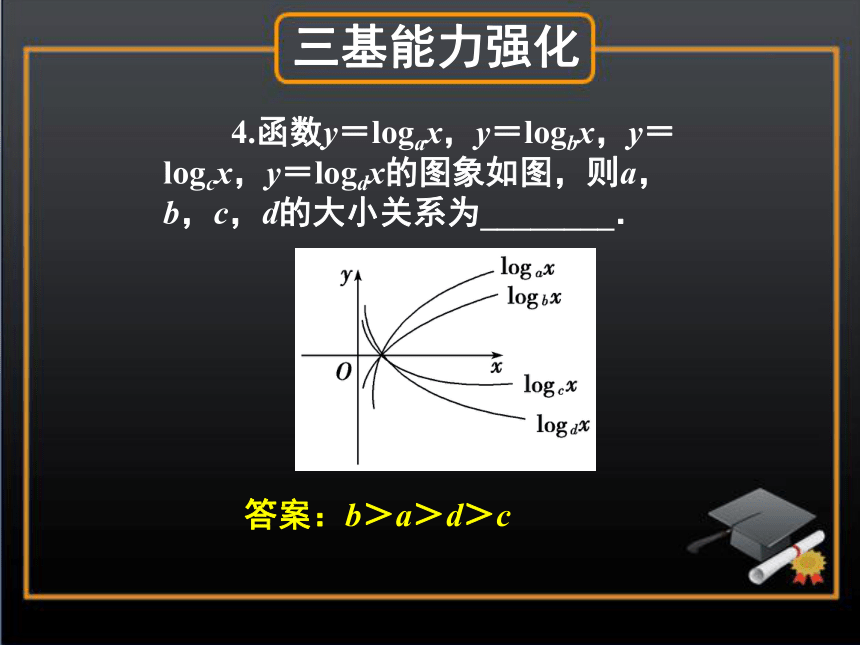
答案：C三基能力强化4.函数y＝logax，y＝logbx，y＝logcx，y＝logdx的图象如图，则a，b，c，d的大小关系为________．三基能力强化答案：b＞a＞d＞c三基能力强化作函数的图象不仅依据函数的解析式，而且还依赖于它的定义域，用两个不同的函数解析式表示的函数，只有在对应法则相同、定义域相同的条件下，才是相同函数，才有相同的图象，作函数图象，除了运用描点法外，还常常利用平移变换、对称变换作函数图象．课堂互动讲练课堂互动讲练作出下列函数的图象．
(1)y＝2x＋1－1；
(2)y＝sin|x|；
(3)y＝|log2(x＋1)|.三基能力强化【解】　(1)y＝2x＋1－1的图象可由y＝2x的图象向左平移1个单位，得y＝2x＋1的图象，再向下平移一个单位得到y＝2x＋1－1的图象，如图①.(2)当x≥0时，y＝sin|x|与y＝sinx的图象完全相同，又y＝sin|x|为偶函数，其图象关于y轴对称，如图②.三基能力强化(3)首先作出y＝log2x的图象c1，然后将c1向左平移1个单位，得到y＝log2(x＋1)的图象c2，再把c2在x轴下方的图象作关于x轴的对称图象，即为所求图象c3：y＝|log2(x＋1)|.如图③(实线部分)．三基能力强化【名师点评】　函数的图象是函数关系的一种直观表示形式，它从“图形”方面刻画了函数的变化规律．通过观察函数的图象，可以形象地揭示函数的有关性质，充分利用函数的图象既有助于记忆函数的性质和变化规律，又能利用数形结合的方法去解决某些问题．三基能力强化例1中函数图象是否具有对称性，有的写出其对称中心或对称轴．
解：(1)，(3)不具有对称性，(2)具有对称性，(2)的对称轴为y轴．课堂互动讲练互动探究对于给定函数的图象，要能从图象的左右、上下分布范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性、周期性，注意图象与函数解析式中参数的关系．课堂互动讲练课堂互动讲练(1)函数y＝f(x)与函数y＝g(x)的图象如图．课堂互动讲练则函数y＝f(x)·g(x)的图象可能是(　　)课堂互动讲练(2)如图，函数的图象由两条射线及抛物线的一部分组成，求函数的解析式．课堂互动讲练【思路点拨】　(1)根据图象可知f(x)和g(x)分别为偶函数和奇函数，结合函数的其他性质，如最值点及其他特殊值即可做出判断．
(2)由题意可知，函数图象是由两条射线和抛物线的一部分组成的，即已知函数的性质，故可采用待定系数法求解．【解】　(1)从f(x)、g(x)的图象可知它们分别为偶函数、奇函数，故f(x)·g(x)是奇函数，排除B.
又∵g(x)的定义域为{x|x≠0}，
故排除C、D.应选A.
(2)设左侧的射线对应的解析式为y＝kx＋b(x≤1)，因为点(1,1)、(0,2)课堂互动讲练课堂互动讲练同理，当x≥3时，右侧射线的解析式为y＝x－2(x≥3)．再设抛物线对应的二次函数的解析式为y＝a(x－2)2＋2(1≤x≤3，a＜0)，因为点(1,1)在抛物线上，所以a＋2＝1，即a＝－1.所以抛物线对应的解析式为y＝－x2＋4x－2(1≤x≤3)．
综上所述，函数的解析式为y＝课堂互动讲练【名师点评】　解决函数图象问题常用方法有：定量分析法、函数模型法、定性分析法．而定性分析法，就是利用图象进行定性地分析而不需要具体计算，它的好处在于我们可以回避定量的繁琐计算．课堂互动讲练函数图象形象地显示了函数的性质，为研究数量关系问题提供了“形”的直观性，它是探求解题途径，获得问题结果的重要工具，要重视数形结合解题的思想方法，常用函数图象研究含参数的方程或不等式解集的情况．课堂互动讲练课堂互动讲练(解题示范)(本题满分12分)
当x∈(1,2)时，不等式(x－1)2 要使当x∈(1,2)时，不等式(x－1)2只需f1(x)＝(x－1)2在(1,2)上的图象在f2(x)＝logax的下方即可. 4分
当01时，如图，要使在(1,2)上，f1(x)＝(x－1)2的图象在f2(x)＝logax的下方，
只需f1(2)≤f2(2)， 10分
即(2－1)2≤loga2，loga2≥1，
∴1＜a≤2. 12分课堂互动讲练【失误点评】　两图象交点(1,0)和(2,1)是否满足条件，不易掌握．(本题满分12分)利用函数图象讨论方程|1－x|＝kx的实数根的个数．课堂互动讲练高考检阅解：设y＝|1－x|，y＝kx，课堂互动讲练则方程的实根的个数就是函数y=|1-x|的图象与y=kx的图象交点的个数.4分
由图象可知：当－1≤k<0时，方程没有实数根；6分
当k＝0或k<－1或k≥1时，方程只有一个实数根；9分
当0研究函数离不开作图，作图的基本方法有两种，一种是描点法，另一种是变换法．变换法作图是应用基本函数的图象，通过平移、伸缩、对称等变换，作出相关函数的图象．应用变换法作图，要求我们熟记基本函数的图象及其性质，准确把握基本函数的图象特征．规律方法总结2．证明图象的对称性时应注意
(1)证明函数图象的对称性，即证明其图象上的任意一点关于对称中心 (或对称轴)的对称点仍在图象上．
(2)证明曲线C1与C2的对称性，即要证明C1上任一点关于对称中心(对称轴)的对称点在C2上，反之亦然．规律方法总结3．知识深化
(1)若f(x)对任意x满足f(a＋x)＝f(a－x)，则f(x)的图象关于直线x＝a对称；反之有结论：f(x)＝f(2a－x)，f(－x)＝f(2a＋x)等；规律方法总结