人教版数学八年级上册 12.2 课时2 三角形全等的判定(SAS)课件(共15张PPT)
文档属性
| 名称 | 人教版数学八年级上册 12.2 课时2 三角形全等的判定(SAS)课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 313.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-25 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
旧知回顾
判定三角形 全等的方法:
1.定义(重合)法;
2.SSS.
12.2.2
三角形全等的判定(2)
先任意画出一个△ABC,再画一个△A′B′C′,使A′B′=AB,∠A ′=∠A,A′C′=AC。把画好的△A′B′C′剪下来看能否与△ABC重合,由此你能得出什么结论?
探究3
已知:任意 △ ABC,画一个△A′B′C′,
使A′B′=AB, ∠A′ =∠A, A′C′=AC.
画法:
1、画∠DA′ E=∠A ;
2、在射线A′ D上截取A′B′=AB,在射线A′ E上截取A′C′=AC;
3、连结B′C′。
△A′B′C′就是所要画的三角形。
问:通过实验可以发现什么事实?
自学P38-39页 ,思考:
①通过上述操作可以发现什么规律?请用符号语言表达。
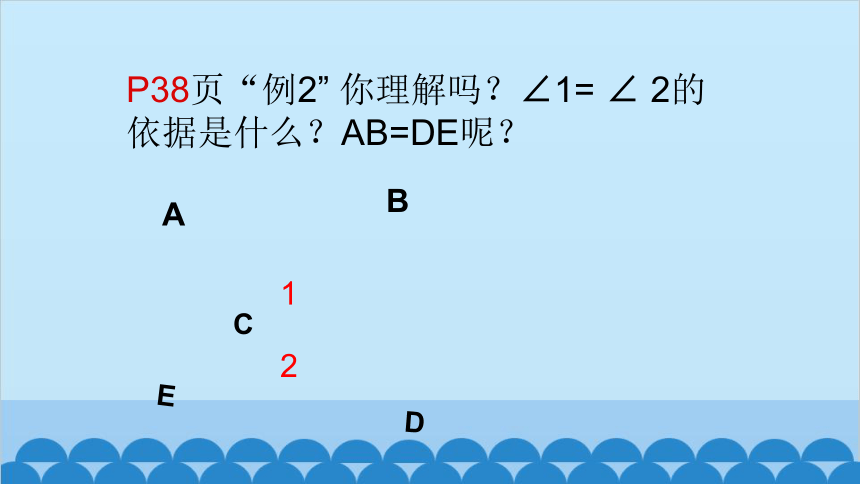
②P38页“例2” 你理解吗?∠1= ∠ 2的依据是什么?AB=DE呢?
③ P39页“思考” 中,△ABD与△ ABC中有几条相等的边,分别是那些?有相等的角吗? △ABD与△ ABC全等吗?这说明了什么?
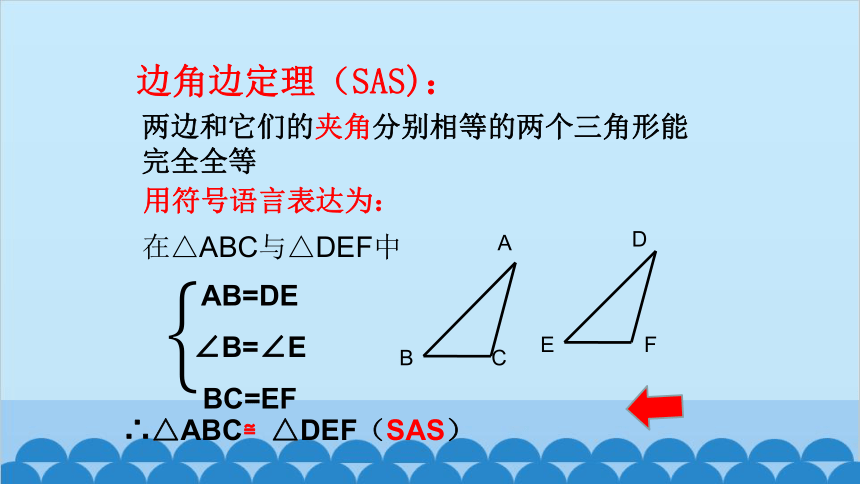
两边和它们的夹角分别相等的两个三角形能完全全等
用符号语言表达为:
在△ABC与△DEF中
∴△ABC≌△DEF(SAS)
A
B
C
D
E
F
AB=DE
∠B=∠E
BC=EF
{
边角边定理(SAS):
P38页“例2” 你理解吗?∠1= ∠ 2的依据是什么?AB=DE呢?
A
B
E
D
C
1
2
B
C
D
A
思考:△ABD与△ ABC中有几条相等的边,分别是哪些?有相等的角吗? △ABD与△ ABC全等吗?这说明了什么?
1、如图:AB=DE=3 ㎝,∠B=∠E=300 , BC=EF=5 ㎝,△ABC≌△ DEF 吗?
3㎝
5㎝
300
A
B
C
3㎝
5㎝
300
D
E
F
当堂练习
课本P39页练习1题
如图:两车从南北方向的路段AB的A端出发,分别向东西行进相同的距离,到达C、D两地。此时C、D到达B的距离相等吗?为什么
如图:点EF在BC上,BE=CF,AB=CD,
∠B= ∠ C。求证 ∠ A= ∠ D
课堂小结
1.两边和它们的夹角对应相等的两个三角形全等。简写成“ ”或“ ” ;
2.到目前为止,我们一共探索出判定三角形全等的2种方法,它们分别是: 。
3. 求证两个三角形中的边或角相等时,一般要先证明这两个三角形 。
A
B
C
D
1、已知:如图AD=CD, BD 平分∠ ADC 。求证:∠A=∠ C。
解:∵ BD 平分∠ ADC
∴ ∠1=∠2
在△ADB与△DBC中
AD=CD
∠1=∠2
BD=BD
∴ △ABD≌△CBD(SAS)
∴ ∠A=∠C(对应角相等)
当堂检测
2、如图,已知AE=AD,AC=AB,请证明∠C= ∠B
A
E
B
D
C
证明: 在△AEC与△ADB中
AD=AE
∠A=∠A
AC=AB
∴ △AEC≌△ADB(SAS)
∴ ∠C=∠B(对应角相等)
A组:课本44页10题,课本55 页3题
绩优学案33页1-9题
B组:课本44页10题,课本55 页3题
绩优学案33页1-8题
课后作业
旧知回顾
判定三角形 全等的方法:
1.定义(重合)法;
2.SSS.
12.2.2
三角形全等的判定(2)
先任意画出一个△ABC,再画一个△A′B′C′,使A′B′=AB,∠A ′=∠A,A′C′=AC。把画好的△A′B′C′剪下来看能否与△ABC重合,由此你能得出什么结论?
探究3
已知:任意 △ ABC,画一个△A′B′C′,
使A′B′=AB, ∠A′ =∠A, A′C′=AC.
画法:
1、画∠DA′ E=∠A ;
2、在射线A′ D上截取A′B′=AB,在射线A′ E上截取A′C′=AC;
3、连结B′C′。
△A′B′C′就是所要画的三角形。
问:通过实验可以发现什么事实?
自学P38-39页 ,思考:
①通过上述操作可以发现什么规律?请用符号语言表达。
②P38页“例2” 你理解吗?∠1= ∠ 2的依据是什么?AB=DE呢?
③ P39页“思考” 中,△ABD与△ ABC中有几条相等的边,分别是那些?有相等的角吗? △ABD与△ ABC全等吗?这说明了什么?
两边和它们的夹角分别相等的两个三角形能完全全等
用符号语言表达为:
在△ABC与△DEF中
∴△ABC≌△DEF(SAS)
A
B
C
D
E
F
AB=DE
∠B=∠E
BC=EF
{
边角边定理(SAS):
P38页“例2” 你理解吗?∠1= ∠ 2的依据是什么?AB=DE呢?
A
B
E
D
C
1
2
B
C
D
A
思考:△ABD与△ ABC中有几条相等的边,分别是哪些?有相等的角吗? △ABD与△ ABC全等吗?这说明了什么?
1、如图:AB=DE=3 ㎝,∠B=∠E=300 , BC=EF=5 ㎝,△ABC≌△ DEF 吗?
3㎝
5㎝
300
A
B
C
3㎝
5㎝
300
D
E
F
当堂练习
课本P39页练习1题
如图:两车从南北方向的路段AB的A端出发,分别向东西行进相同的距离,到达C、D两地。此时C、D到达B的距离相等吗?为什么
如图:点EF在BC上,BE=CF,AB=CD,
∠B= ∠ C。求证 ∠ A= ∠ D
课堂小结
1.两边和它们的夹角对应相等的两个三角形全等。简写成“ ”或“ ” ;
2.到目前为止,我们一共探索出判定三角形全等的2种方法,它们分别是: 。
3. 求证两个三角形中的边或角相等时,一般要先证明这两个三角形 。
A
B
C
D
1、已知:如图AD=CD, BD 平分∠ ADC 。求证:∠A=∠ C。
解:∵ BD 平分∠ ADC
∴ ∠1=∠2
在△ADB与△DBC中
AD=CD
∠1=∠2
BD=BD
∴ △ABD≌△CBD(SAS)
∴ ∠A=∠C(对应角相等)
当堂检测
2、如图,已知AE=AD,AC=AB,请证明∠C= ∠B
A
E
B
D
C
证明: 在△AEC与△ADB中
AD=AE
∠A=∠A
AC=AB
∴ △AEC≌△ADB(SAS)
∴ ∠C=∠B(对应角相等)
A组:课本44页10题,课本55 页3题
绩优学案33页1-9题
B组:课本44页10题,课本55 页3题
绩优学案33页1-8题
课后作业
