24.4三角形的中位线
图片预览



文档简介
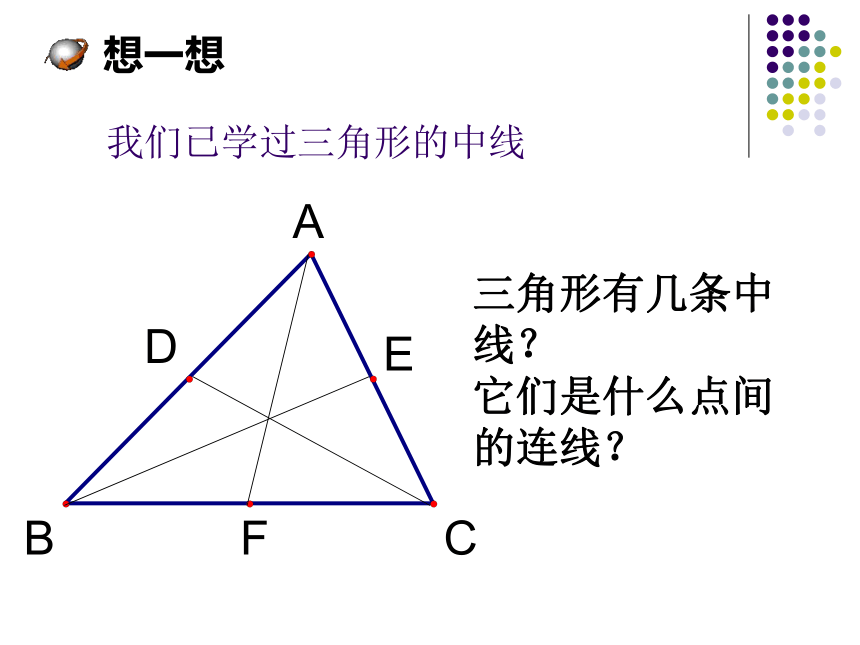
课件21张PPT。1.三角形的中位线(1)24.4中位线义务教育课程标准实验教科书华东师大版 我们已学过三角形的中线 三角形有几条中线?
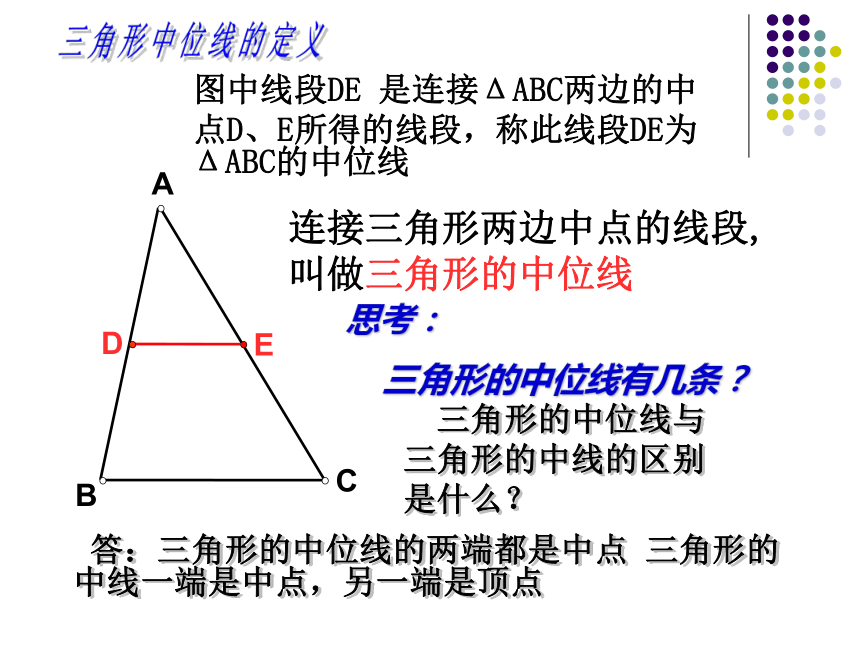
它们是什么点间的连线? 想一想CBAED连接三角形两边中点的线段,叫做三角形的中位线三角形中位线的定义思考:
三角形的中位线有几条? 图中线段DE 是连接ΔABC两边的中
点D、E所得的线段,称此线段DE为ΔABC的中位线 三角形的中位线与
三角形的中线的区别
是什么?
答:三角形的中位线的两端都是中点 三角形的中线一端是中点,另一端是顶点
如图, △ABC 中,点D、E分别
是AB与AC的中点,
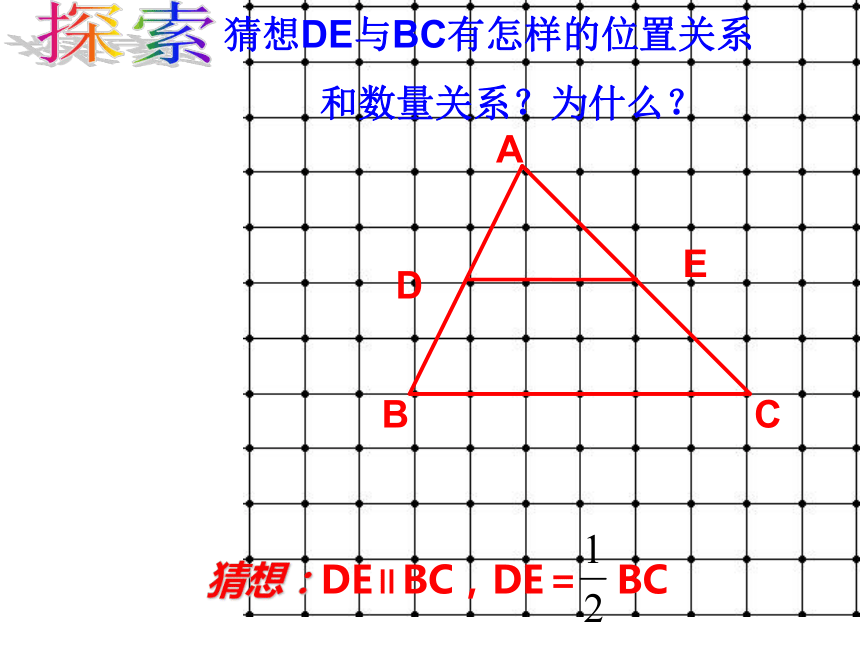
(1)证明: △ADE∽ △ABC.(2)猜想DE与BC有怎样的位置关系
和数量关系?为什么?ABCDE探索猜想:DE∥BC,DE= BC猜想DE与BC有怎样的位置关系
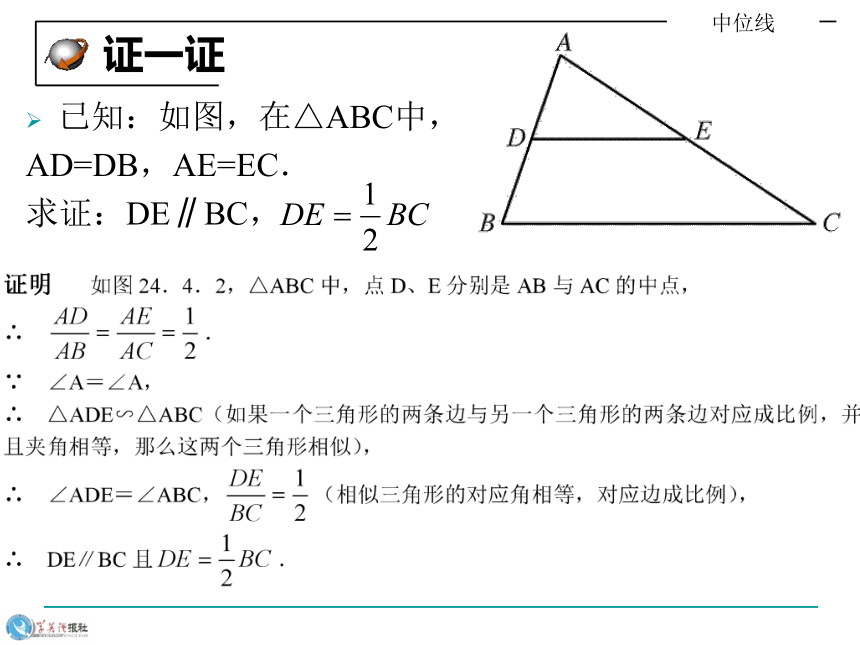
和数量关系?为什么?已知:如图,在△ABC中,
AD=DB,AE=EC.
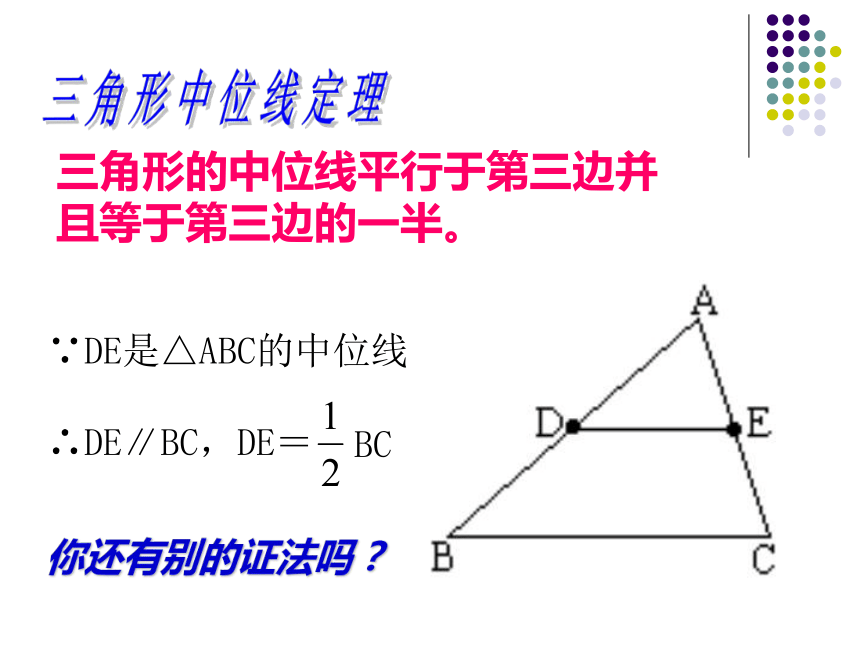
求证:DE∥BC, 证一证三角形中位线定理∵DE是△ABC的中位线
∴DE∥BC,DE=BC 三角形的中位线平行于第三边并且等于第三边的一半。你还有别的证法吗?三角形中位线的性质:
三角形的中位线平行于
第三边并且等于第三边的
一半。
此性质的特点:同一条件下有2个结论
因为DE为ΔABC的中位线
所以①DE∥BC,②DE=?BC
↓ ↓
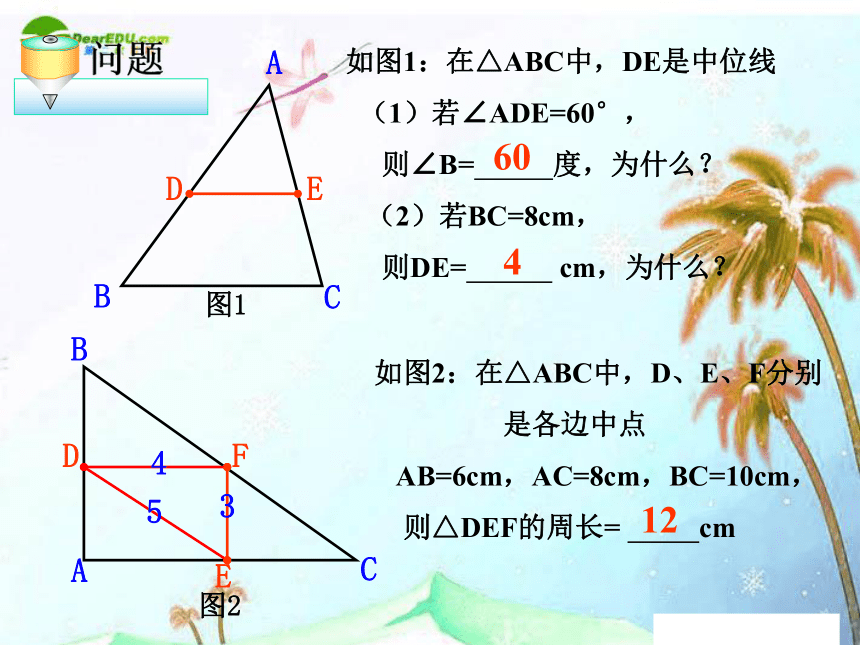
位置关系 数量关系 如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么? 如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长= cm图1图260412ABCD EBACD EF543练一练:(2)若△ABC的三条中位线围成的三角形周长为15cm, △ABC的周长是____。(1)若△ABC三边AB、AC、BC的长分别为8、6、 4,它的三条中位线围成的△DEF的周长_____。(3)若△ABC的三条中位线长分别为3、4、5,则△ABC的周长为 面积为 。 N 4、已知:在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,
N是AB的中点.求证∠PMN=∠PNM.例1 求证三角形的一条中位线与
第三边上的中线互相平分.例1、求证三角形的一条中位线与第三边上的中线互相平分. ABCDE已知:如图,在△ABC中, AD=DB,AE=EC,BF=FC
求证:DE、AF互相平分F证明:连结DF、EF
∵AD=DB,BE=CE
∴DE∥AC(三角形中位线定理)
同理EF∥AB
∴四边形ADEF是平行四边形
∴DE、AF互相平分
(平行四边形的对角线互相平分) 运用例2 已知:如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点
求证:四边形EFGH是平行四边形. 运用 运用 拓展思考猜一猜:画一个任意四边形,并画出四边的
中点,再顺次连接四边形的中点,得到的四边
形的形状是什么?如图,四边形ABCD中,E F G H分别是
AB CD AD BC的中点,四边形EFGH是
平行四边形吗?为什么?
⑴顺次连接任意四边形四边中点所得的四边形是平行四边形议一议:顺次连接矩形的四边中点所得的四边形
是什么形状?为什么? 如果将“矩形”改成“菱形”呢?⑵顺次连接矩形的四边中点所得的四边形是菱形⑶顺次连接菱形的四边中点所得的四边形是矩形结论: 议一议:1.如果顺次连接四边形四边中点所得的四边形是菱形,那么原四边形的两条对角线存在什么关系 ? (两条对角线相等)2.上问中的菱形改为矩形呢?
(两条对角线互相垂直)3.当四边形满足什么条件时,顺次连接它的四边中点 所得的四边形是正方形?(两条对角线互相垂直且相等)
课堂训练 练一练:1。如图(1)ΔABC中,
AB=6㎝, AC=8㎝,BC=10㎝,
D﹑E﹑F分别是ABACBC的中点
则ΔDEF的周长是____ ,
面积是____。 2.如图(2)ΔABC中,DE是
中位线,AF是中线,则DE与
AF的关系是____3.若顺次连接四边形四边中
点所得的四边形是菱形,则
原四边形( )
(A)一定是矩形 (B)一定是菱形
(C)对角线一定互相垂直 (D)对角线一定相等
FACBDEF(2)互相平分6cm212cmD说一说你学到了什么?1.理解三角形中位线的概念:连接三角形两边的中点的线段叫做三角形的中位线。
2.掌握三角形中位线的性质:三角形的中位线平行于第三边,并且等于第三边的一半。
4.能应用三角形中位线的性质解决有关计算或说理等问题。
它们是什么点间的连线? 想一想CBAED连接三角形两边中点的线段,叫做三角形的中位线三角形中位线的定义思考:
三角形的中位线有几条? 图中线段DE 是连接ΔABC两边的中
点D、E所得的线段,称此线段DE为ΔABC的中位线 三角形的中位线与
三角形的中线的区别
是什么?
答:三角形的中位线的两端都是中点 三角形的中线一端是中点,另一端是顶点
如图, △ABC 中,点D、E分别
是AB与AC的中点,
(1)证明: △ADE∽ △ABC.(2)猜想DE与BC有怎样的位置关系
和数量关系?为什么?ABCDE探索猜想:DE∥BC,DE= BC猜想DE与BC有怎样的位置关系
和数量关系?为什么?已知:如图,在△ABC中,
AD=DB,AE=EC.
求证:DE∥BC, 证一证三角形中位线定理∵DE是△ABC的中位线
∴DE∥BC,DE=BC 三角形的中位线平行于第三边并且等于第三边的一半。你还有别的证法吗?三角形中位线的性质:
三角形的中位线平行于
第三边并且等于第三边的
一半。
此性质的特点:同一条件下有2个结论
因为DE为ΔABC的中位线
所以①DE∥BC,②DE=?BC
↓ ↓
位置关系 数量关系 如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么? 如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长= cm图1图260412ABCD EBACD EF543练一练:(2)若△ABC的三条中位线围成的三角形周长为15cm, △ABC的周长是____。(1)若△ABC三边AB、AC、BC的长分别为8、6、 4,它的三条中位线围成的△DEF的周长_____。(3)若△ABC的三条中位线长分别为3、4、5,则△ABC的周长为 面积为 。 N 4、已知:在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,
N是AB的中点.求证∠PMN=∠PNM.例1 求证三角形的一条中位线与
第三边上的中线互相平分.例1、求证三角形的一条中位线与第三边上的中线互相平分. ABCDE已知:如图,在△ABC中, AD=DB,AE=EC,BF=FC
求证:DE、AF互相平分F证明:连结DF、EF
∵AD=DB,BE=CE
∴DE∥AC(三角形中位线定理)
同理EF∥AB
∴四边形ADEF是平行四边形
∴DE、AF互相平分
(平行四边形的对角线互相平分) 运用例2 已知:如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点
求证:四边形EFGH是平行四边形. 运用 运用 拓展思考猜一猜:画一个任意四边形,并画出四边的
中点,再顺次连接四边形的中点,得到的四边
形的形状是什么?如图,四边形ABCD中,E F G H分别是
AB CD AD BC的中点,四边形EFGH是
平行四边形吗?为什么?
⑴顺次连接任意四边形四边中点所得的四边形是平行四边形议一议:顺次连接矩形的四边中点所得的四边形
是什么形状?为什么? 如果将“矩形”改成“菱形”呢?⑵顺次连接矩形的四边中点所得的四边形是菱形⑶顺次连接菱形的四边中点所得的四边形是矩形结论: 议一议:1.如果顺次连接四边形四边中点所得的四边形是菱形,那么原四边形的两条对角线存在什么关系 ? (两条对角线相等)2.上问中的菱形改为矩形呢?
(两条对角线互相垂直)3.当四边形满足什么条件时,顺次连接它的四边中点 所得的四边形是正方形?(两条对角线互相垂直且相等)
课堂训练 练一练:1。如图(1)ΔABC中,
AB=6㎝, AC=8㎝,BC=10㎝,
D﹑E﹑F分别是ABACBC的中点
则ΔDEF的周长是____ ,
面积是____。 2.如图(2)ΔABC中,DE是
中位线,AF是中线,则DE与
AF的关系是____3.若顺次连接四边形四边中
点所得的四边形是菱形,则
原四边形( )
(A)一定是矩形 (B)一定是菱形
(C)对角线一定互相垂直 (D)对角线一定相等
FACBDEF(2)互相平分6cm212cmD说一说你学到了什么?1.理解三角形中位线的概念:连接三角形两边的中点的线段叫做三角形的中位线。
2.掌握三角形中位线的性质:三角形的中位线平行于第三边,并且等于第三边的一半。
4.能应用三角形中位线的性质解决有关计算或说理等问题。
