人教版数学七年级上册 1.3.2 有理数的减法 第2课时 课件(共17张PPT)
文档属性
| 名称 | 人教版数学七年级上册 1.3.2 有理数的减法 第2课时 课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 514.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-26 08:21:01 | ||
图片预览






文档简介
(共17张PPT)
1.3.2 有理数的减法
第2课时
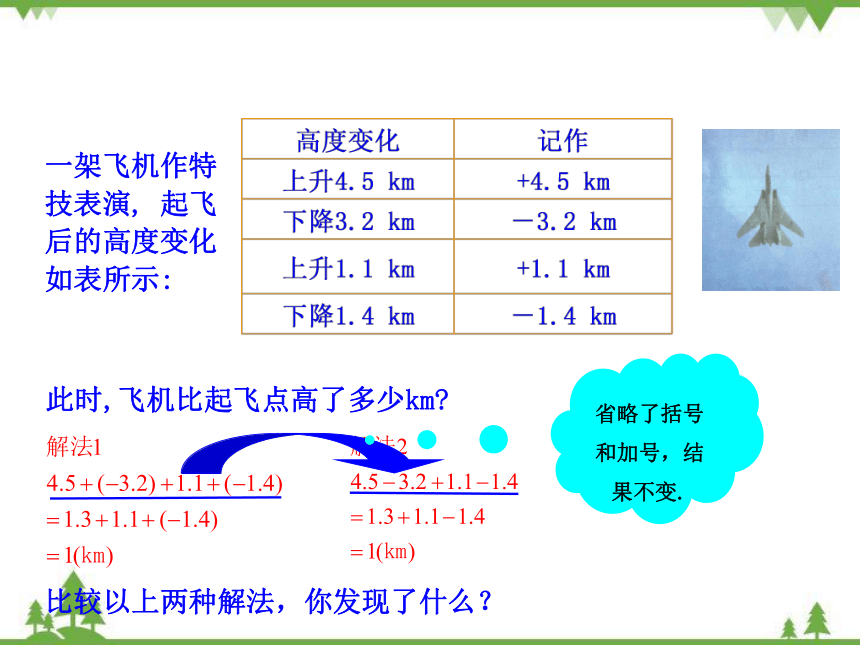
一架飞机作特技表演, 起飞后的高度变化如表所示:
此时,飞机比起飞点高了多少km
比较以上两种解法,你发现了什么?
省略了括号和加号,结果不变.
1.能够把有理数的减法运算转化为加法运算,进 而写成省略括号和加号的和的形式.
2.准确熟练进行有理数加减混合运算.
例1 计算(-20)+(+3)-(-5)-(+7).
分析:这个式子中有加法,也有减法,可以根据有理数减法法则,把它改写为
(-20)+(+3)+(+5)+(-7)
使问题转化为几个有理数的加法.
【解析】(-20)+(+3)-(-5)-(+7)
=(-20)+(+3)+(+5)+(-7)
=[(-20)+(-7)]+[(+5)+(+3)]
=(-27)+(+8)
=-19
以上步骤运用了什么运算律?
【例题】
解法指导:要先把减法化成加法,再依据加法法则进行计算.
【跟踪训练】
答案:-30.
答案:-10.
答案:168.
答案:-20.
将下列式子先统一成加法,再写成省略加号和括号的和的形式.
1.(-40)-(+27)+19-24-(-32).
2. -9-(-2)+(-3)-4.
观察下列式子,你能发现简化符号的什么规律?
(-40)-(+27)+19-24-(-32)
=-40-27+19-24+32.
-9-(-2)+(-3)-4
=-9 + 2 - 3-4.
规律:
数字前“-”号是奇数个取“-”;
数字前“-”号是偶数个取“+”.
例2 计算:
解法指导:先写成省略括号的和的形式,并把小数化为分数,再根据运算律进行合理运算.
【例题】
答案:(1) (2)-2 (3)
(4) (5) (6)-3
【跟踪训练】
在数轴上,点 A,B 分别表示 a,b.利用有理数减法,分别计算下列情况下点 A,B 之间的距离;
a=2,b=6; a=0,b=6;
a=2,b=-6; a=-2,b=-6.
你能发现点 A, B 之间的距离与数 a,b 之间的关系吗?
数轴上分别表示数a、b的A、B两点间距离公式为 AB=|b-a|.
4
6
8
4
加减混合运算
统一为加法运算
省略括号和加号的和的形式
规律:
数字前“-”号是奇数个取“-”;
数字前“-”号是偶数个取“+”.
1.计算:
答案:(1)-2.7 (2) (3)-30 (4) (5)45.5 (6)
.
.
.
.
.
.
2.在数轴上,点A、B分别表示数a、b.利用有
理数减法,分别计算下列情况下点A、B之间的距离;
(1)a=-1,b=6;(2)a=1,b=-6;
(3)a=-1,b=-6;(4)a=1,b=6.
解:(1)AB=|b-a|=|6-(-1)|=7;
(2)AB=|b-a|=|-6-1|=7;
(3)AB=|b-a|=|-6-(-1)|=5;
(4)AB=|b-a|=|6-1|=5.
3.一辆货车从超市出发,向东走了3 km到达小彬家,继续走了1.5 km到达小颖家,然后向西走了9.5 km到达小明家,最后回到超市.
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1 km,你能在数轴上表示出小明家、小彬家和小颖家的位置吗?
(2)小明家距小彬家多远?
(3)货车一共行驶了多少km?
解:
0
-5
4.5
3
超市
小彬家
小颖家
小明家
(2)3-(-5)=3+5=8(km).
(3)∣3∣+∣1.5∣+∣-9.5∣+∣5∣=3+1.5+9.5+5 =19(km)
答:小明家距小彬家8km. 货车一共行驶了19km.
(1)
从来没有人读书,只有人在书中读自己,发现
自己或检查自己.
——罗曼·罗兰
1.3.2 有理数的减法
第2课时
一架飞机作特技表演, 起飞后的高度变化如表所示:
此时,飞机比起飞点高了多少km
比较以上两种解法,你发现了什么?
省略了括号和加号,结果不变.
1.能够把有理数的减法运算转化为加法运算,进 而写成省略括号和加号的和的形式.
2.准确熟练进行有理数加减混合运算.
例1 计算(-20)+(+3)-(-5)-(+7).
分析:这个式子中有加法,也有减法,可以根据有理数减法法则,把它改写为
(-20)+(+3)+(+5)+(-7)
使问题转化为几个有理数的加法.
【解析】(-20)+(+3)-(-5)-(+7)
=(-20)+(+3)+(+5)+(-7)
=[(-20)+(-7)]+[(+5)+(+3)]
=(-27)+(+8)
=-19
以上步骤运用了什么运算律?
【例题】
解法指导:要先把减法化成加法,再依据加法法则进行计算.
【跟踪训练】
答案:-30.
答案:-10.
答案:168.
答案:-20.
将下列式子先统一成加法,再写成省略加号和括号的和的形式.
1.(-40)-(+27)+19-24-(-32).
2. -9-(-2)+(-3)-4.
观察下列式子,你能发现简化符号的什么规律?
(-40)-(+27)+19-24-(-32)
=-40-27+19-24+32.
-9-(-2)+(-3)-4
=-9 + 2 - 3-4.
规律:
数字前“-”号是奇数个取“-”;
数字前“-”号是偶数个取“+”.
例2 计算:
解法指导:先写成省略括号的和的形式,并把小数化为分数,再根据运算律进行合理运算.
【例题】
答案:(1) (2)-2 (3)
(4) (5) (6)-3
【跟踪训练】
在数轴上,点 A,B 分别表示 a,b.利用有理数减法,分别计算下列情况下点 A,B 之间的距离;
a=2,b=6; a=0,b=6;
a=2,b=-6; a=-2,b=-6.
你能发现点 A, B 之间的距离与数 a,b 之间的关系吗?
数轴上分别表示数a、b的A、B两点间距离公式为 AB=|b-a|.
4
6
8
4
加减混合运算
统一为加法运算
省略括号和加号的和的形式
规律:
数字前“-”号是奇数个取“-”;
数字前“-”号是偶数个取“+”.
1.计算:
答案:(1)-2.7 (2) (3)-30 (4) (5)45.5 (6)
.
.
.
.
.
.
2.在数轴上,点A、B分别表示数a、b.利用有
理数减法,分别计算下列情况下点A、B之间的距离;
(1)a=-1,b=6;(2)a=1,b=-6;
(3)a=-1,b=-6;(4)a=1,b=6.
解:(1)AB=|b-a|=|6-(-1)|=7;
(2)AB=|b-a|=|-6-1|=7;
(3)AB=|b-a|=|-6-(-1)|=5;
(4)AB=|b-a|=|6-1|=5.
3.一辆货车从超市出发,向东走了3 km到达小彬家,继续走了1.5 km到达小颖家,然后向西走了9.5 km到达小明家,最后回到超市.
(1)以超市为原点,以向东的方向为正方向,用1个单位长度表示1 km,你能在数轴上表示出小明家、小彬家和小颖家的位置吗?
(2)小明家距小彬家多远?
(3)货车一共行驶了多少km?
解:
0
-5
4.5
3
超市
小彬家
小颖家
小明家
(2)3-(-5)=3+5=8(km).
(3)∣3∣+∣1.5∣+∣-9.5∣+∣5∣=3+1.5+9.5+5 =19(km)
答:小明家距小彬家8km. 货车一共行驶了19km.
(1)
从来没有人读书,只有人在书中读自己,发现
自己或检查自己.
——罗曼·罗兰
